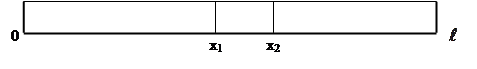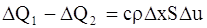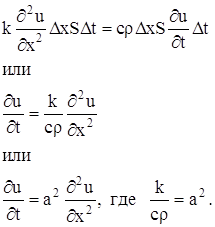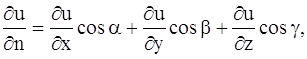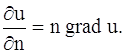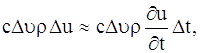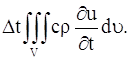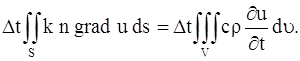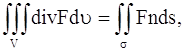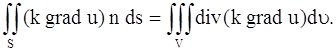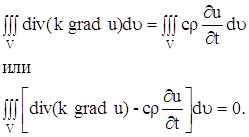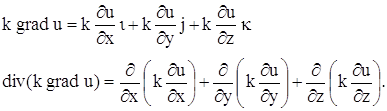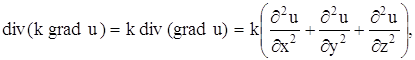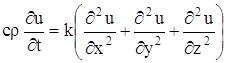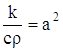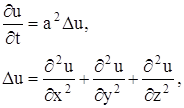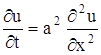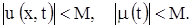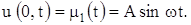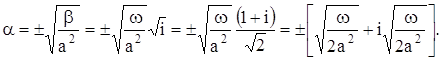При построении математической модели распространения тепла в стержне сделаем следующие предположения:
1) стержень сделан из однородного проводящего материала с плотностью ρ;
2) боковая поверхность стержня теплоизолирована, то есть тепло может распространяться только вдоль оси ОХ;
3) стержень тонкий — это значит, что температура во всех точках любого поперечного сечения стержня одна и та же.
Рассмотрим часть стержня на отрезке [х, х + ∆х] (см. рис. 6) и воспользуемся законом сохранения количества тепла:
Общее количество тепла на отрезке [х, х + ∆х] = полному количеству тепла, прошедшему через границы + полное количество тепла, образованного внутренними источниками.
Общее количество тепла, которое необходимо сообщить участку стержня, чтобы повысить его температуру на ∆U, вычисляется по формуле: ∆Q= CρS∆x∆U, где С — удельная теплоемкость материала ( = количеству тепла, которое нужно сообщить 1 кг вещества, чтобы поднять его температуру на 1°), S — площадь поперечного сечения.
Количество тепла, прошедшее через левый конец участка стержня за время ∆t (тепловой поток) вычисляется по формуле: Q1 = -kSUx(x, t)∆t, где k — коэффициент теплопроводности материала ( = количеству тепла, протекающего в секунду через стержень единичной длины и единичной площади поперечного сечения при разности температур на противоположных концах, равной 1°). В этой формуле особого пояснения требует знак минус. Дело в том, что поток считается положительным, если он направлен в сторону увеличения х, а это, в свою очередь, означает, что слева от точки х температура больше, чем справа, то есть Ux CpS∆x∆U = kSUx(x + ∆х, t) ∆t — kSUx(x, t)∆t.
Если это равенство поделить на S∆x∆t и устремить ∆х и ∆t к нулю, то будем иметь:
Отсюда уравнение теплопроводности имеет вид
Ut = a 2 Uxx,
где 
В случае, когда внутри стержня имеются источники тепла, непрерывно распределенные с плотностью q(x,t), получится неоднородное уравнение теплопроводности
Начальные условия и граничные условия.
Для уравнения теплопроводности задается только одно начальное условие U|t=0 = φ(х) (или в другой записи U(x,0) = φ(х)) и физически оно означает, что начальное распределение температуры стержня имеет вид φ(х). Для уравнений теплопроводности на плоскости или в пространстве начальное условие имеет такой же вид, только функция φ будет зависеть, соответственно, от двух или трех переменных.
Граничные условия в случае уравнения теплопроводности имеют такой же вид, как и для волнового уравнения, но физический смысл их уже иной. Условия первого рода (5) означают, что на концах стержня задана температура. Если она не изменяется со временем, то g1(t) ≡ Т1 и g2(t) ≡ Т2, где Т1 и Т2 — постоянные. Если концы поддерживаются все время при нулевой температуре, то Т1= Т2 = 0 и условия будут однородными. Граничные условия второго рода (6) определяют тепловой поток на концах стержня. В частности, если g1(t) = g2(t) = 0, то условия становятся однородными. Физически они означают, что через концы не происходит теплообмен с внешней средой (эти условия еще называют условиями теплоизоляции концов). Наконец, граничные условия третьего рода (7) соответствуют случаю, когда через концы стержня происходит теплообмен с окружающей средой по закону Ньютона (напомним, что при выводе уравнения теплопроводности мы считали боковую поверхность теплоизолированной). Правда, в случае уравнения теплопроводности условия (7) записываются немного по-другому:
Физический закон теплообмена со средой (закон Ньютона) состоит в том, что поток тепла через единицу поверхности в единицу времени пропорционален разности температур тела и окружающей среды. Таким образом, для левого конца стержня он равен Здесь h1 > 0 — коэффициент теплообмена с окружающей средой, g1(t) — температура окружающей среды на левом конце. Знак минус поставлен в формуле по той же причине, что и при выводе уравнения теплопроводности. С другой стороны, в силу теплопроводности материала поток тепла через этот же конец равен Применив закон сохранения количества тепла, получим:
Аналогично получается условие (14) на правом конце стержня, только постоянная λ2 может быть другой, так как, вообще говоря, среды, окружающие левый и правый конец, бывают разные.
Граничные условия (14) являются более общими по сравнению с условиями первого и второго рода. Если предположить, что через какой-либо конец не происходит теплообмена со средой (то есть коэффициент теплообмена равен нулю), то получится условие второго рода. В другом случае предположим, что коэффициент теплообмена, например h1, очень большой.
Перепишем условие (14) при х = 0 в виде и устремим . В результате будем иметь условие первого рода:
Аналогично формулируются граничные условия и для большего числа переменных. Для задачи о распространении тепла в плоской пластине условие означает, что температура на ее краях поддерживается нулевой. Точно так же, условия и внешне очень похожи, но в первом случае оно означает, что рассматривается плоская пластина и края ее теплоизолированы, а во втором случае оно означает, что рассматривается задача о распространении тепла в теле и поверхность его теплоизолирована.
Решение первой начально-краевой задачи для уравнения теплопроводности.
Рассмотрим однородную первую начально-краевую задачу для уравнения теплопроводности:
Найти решение уравнения
удолетворяющее граничным условиям
и начальному условию
Решим эту задачу методом Фурье.
Шаг 1. Будем искать решения уравнения (15) в виде U(x,t) = X(x)T(t).
Найдем частные производные:
Подставим эти производные в уравнение и разделим переменные:
По основной лемме получим
Теперь можно решить каждое из этих обыкновенных дифференциальных уравнений. Обратим внимание на то, что используя граничные условия (16), можно искать не общее решение уравнения б), а частные решения, удолетворяющие соответствующим граничным условиям:
Шаг 2. Решим задачу Штурма-Лиувилля
Эта задача совпадает с задачей Штурма-Лиувилля, рассмотренной в лекции 3. Напомним, что собственные значения и собственные функции этой задачи существуют только при λ>0.
Собственные значения равны
Собственные функции равны (См. решение задачи)
Шаг 3. Подставим собственные значения в уравнение а) и решим его:
Шаг 4. Выпишем частные решения уравнения (15):
В силу линейности и однородности уравнения (15) их линейная комбинация
Шаг 5. Определим коэффициенты An в (19), используя начальное условие (17):
Приходим к тому, что начальная функция φ(x) разлагается в ряд Фурье по собственным функциям задачи Штурма-Лиувилля. По теореме Стеклова такое разложение возможно для функций, удовлетворяющих граничным условиям и имеющих непрерывные производные второго порядка. Коэффициенты Фурье находятся по формулам
Вычислив эти коэффициенты для конкретной начальной функции φ(x) и подставив их значения в формулу (19), мы тем самым получим решение задачи (15), (16), (17).
Замечание. Используя формулу (19), можно также, как в лекции 3, получить решение первой начально-краевой задачи для уравнения Ut = a 2 Uxx. Оно будет иметь вид
где
Видео:Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Распространение тепла в стержне
Оглавление
1 Уравнения в частных производных. 3
2 Распространение тепла в стержне. 4
3 Метод Фурье для одномерного уравнения теплопроводности. Распространение тепла в ограниченном стержне. 6
4 Решение задачи спектральным методом.. 11
Список источников. 16
Введение
В данной работе рассматриваются методы решения уравнения распространения тепла в стержне. В первой части работы рассматриваются уравнения в частных производных. Эти уравнения называются основными уравнениями математической физики. Они описывают физические процессы, относящиеся к области механики сплошных сред. Именно этим и объясняется название курса «Уравнения математической физики». Во второй части речь идет об основных уравнениях математической физики полученных на основе общих законов физики, описывающие распространение тепла в стержне. Далее, более подробно, рассматривается метод Фурье для одномерного уравнения теплопроводности, так же известный как метод разделения переменных. В заключительной части работы описывается спектральный способ решения данной задачи, с использованием программного обеспечения Matlab/Octave.
Уравнения в частных производных
Уравнением с частными производными относительно функции u(x1,…,xn) называется уравнение, содержащее хотя бы одну из частных производных этой функции. Порядком уравнения с частными производными называется порядок наивысшей производной входящей в это уравнение. Дифференциальное уравнение с частными производными называется линейным, если искомая функция и ее частные производные входят в него линейно (т.е. в первой степени) [1]
Решение уравнения в частных производных может содержать произвольные функции, в отличие от обыкновенных дифференциальных уравнений, решение которых может содержать лишь произвольные постоянные.
Очевидно, что функция U(x,y) = j(y) есть решение уравнения 
Наибольший практический интерес представляют дифференциальные уравнения второго порядка. В частности, линейное уравнение с частными производными второго порядка с искомой функцией U(x 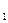



Если f(x1,x2. xn) = 0, то уравнение (1) называется линейным однородным уравнением, в противном случае — линейным неоднородным.
Среди уравнений с частными производными второго порядка следует выделить три типа, которые для функций двух независимых переменных имеют
| Волновое уравнение (уравнение гиперболического типа) |  (2) (2) |
| Уравнение теплопроводности или уравнение Фурье (уравнение параболического типа) |  (3) (3) |
| Уравнение Лапласа (уравнение эллиптического вида) |  (4) (4) |
Распространение тепла в стержне
Основные уравнения математической физики получены на основе общих законов физики. Получим уравнение теплопроводности, рассматривая процесс теплопередачи в однородном ограниченном стержне длиной l. Будем считать,
что боковая поверхность теплоизолирована, а температура в поперечном сечении одинакова. Один конец стержня расположен в точке x = 0, тогда другой конец будет иметь координату x = l.
Пусть T(x,t) — температура в точке x в момент времени t.
Скорость распространения тепла (количество тепла протекающего через поперечное сечение стержня с абсциссой x за единицу времени) установлена опытным путем:

Рассмотрим элемент стержня, заключенный между сечениями с абсциссой x1 и x2. Обозначим Dx = x2 – x1. Через сечение с абсциссой x1 за время Dt пройдет количество тепла равное 
То же самое, для сечения с абсциссой x2: 
где 


Приток тепла в рассматриваемый элемент стержня за время Dt будет:




В выражении (5) применена теорема Лагранжа 
В результате этого притока тепла температура в рассматриваемом элементе стержня изменяется на величину DT, т.е.
или DQ1 -DQ2 @ С× r×Dx×S× 
где С – теплоемкость вещества стержня;
r — плотность вещества стержня.
Приравнивая (5) и (6) получим: l 
Или 


Уравнение теплопроводности в стержне примет вид:

Это простейшее уравнение параболического типа.
Рассматривая процесс распространения тепла в 3-х мерном пространстве, где температура Т(x,y,z,t) является функцией координат (x,y,z) и времени t, можно получить уравнение теплопроводности в виде:

Если функция Т(x,y,z,t) не зависит от z, т.е. температура не зависит от z, то получим уравнение распространения тепла на плоскости:



Коэффициент a 2 имеет тот же смысл что и в уравнении (7).
Видео:075 Динамика распространения тепла в стержнеСкачать

Уравнение распространения тепла в стержне
2.1.1. Уравнение распространения тепла в стержне.
Рассмотрим однородный стержень длины 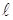
Расположим ось Ох так, что один конец стержня будет совпадать с точкой х = 0, а другой – с точкой х = 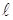
Пусть u (x, t) – температура в сечении стержня с абсциссой х в момент t. Опытным путем установлено, что скорость распространения тепла, т. е. количество тепла, протекающего через сечение с абсциссой х за единицу времени, определяется формулой
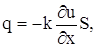
где S – площадь сечения рассматриваемого стержня, k – коэффициент теплопроводности.
Рассмотрим элемент стержня, заключенный между сечениями с абсциссами х1 и х2 (х2 – х1 = 

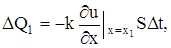
то же самое с абсциссой х2:
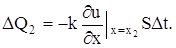
Приток 


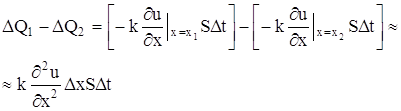
Этот приток тепла за время 

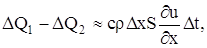
где с – теплоемкость вещества стержня, 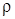

Приравнивая выражения (4) и (5) одного и того же количества тепла 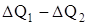
Это и есть уравнение распространения тепла (уравнение теплопроводности) в однородном стержне.
Чтобы решение уравнения (6) было вполне определено, функция u (x, t) должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Краевые условия для решения уравнения (6) могут быть различные. Условия, которые соответствуют так называемой первой краевой задаче для 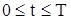
u (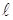
Физическое условие (7) (начальное условие) соответствует тому, что при 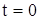
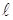
Доказывается, что уравнение (6) имеет единственное решение в области 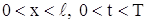
2.1.2. Распространение тепла в пространстве.
Рассмотрим процесс распространения тепла в трехмерном пространстве. Пусть u (x, y, z, t) – температура в точке с координатами (x, y, z) с момент времени t. Опытным путем установлено, что скорость прохождения тепла через площадку 
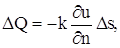
где k – коэффициент теплопроводности рассматриваемой среды, которую мы считаем однородной и изотропной, n – единичный вектор, направленный по нормали к площадке 
где 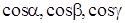
Подставляя выражение 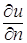


Количество тепла, протекающего за время ∆t через площадку ∆s, будет равно:




Вернемся к поставленной задаче. В рассматриваемой среде выделим малый объем V, ограниченный поверхностью S. Количество тепла, протекающего через поверхность S, будет равно:
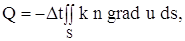
где n – единичный вектор, направленный по внешней нормали к поверхности S. Очевидно, что формула (11) дает количество тепла, поступающего в объем V (или уходящего из объема V) за время 
Рассмотрим элементарный объем 



где с – теплоемкость вещества, ρ – плотность. Общее количество тепла, затраченное на повышение температуры в объеме V за время 
Но это есть тепло, поступающее в объем V за время 
Сокращая на 
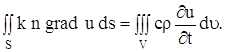
Поверхностный интеграл, стоящий в левой части этого равенства, преобразуем по формуле Остроградского (в векторной форме, где F – дивергенция векторного поля, 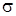
полагая F = k grad u:
Заменяя двойной интеграл, стоящий в левой части равенства (12), тройным интегралом, получим:
Применив теорему о среднем к тройному интегралу, стоящего слева, получим :
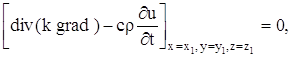
где P (x, y, z) – некоторая точка объема V.
Так как мы можем выделить произвольный объем V в трехмерном пространстве, где происходит распространение тепла, и так как мы предполагаем, что подынтегральная функция в равенстве (13) непрерывна, то равенство (14) будет выполняться в каждой точке пространства. Итак,
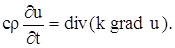
Подставляя в уравнение (15), получаем:
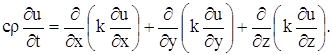
Если k – постоянное, то
и уравнение (15) в этом случае дает:
или, положив
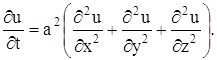
Коротко уравнение (17) записывается так:
где 
Пусть имеем тело 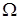
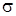
u (x, y, z, 0) = φ (x, y, z). (18)
Кроме того, должна быть известна температура в любой точке М поверхности 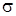
u (М, t) = ψ (М, t). (19)
(Возможны и другие граничные условия.)
Если искомая функция u (x, y, z, t) не зависит от z, что соответствует тому, что температура не зависит от z, то получаем уравнение:
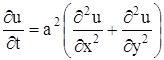
— уравнение распространения тепла на плоскости. Если рассматривается распространения тепла в плоской области D с границей С, то граничные условия, аналогично (18) и (19), формулируются так:
где φ и ψ – заданные функции, М – точка границы С.
Если же функция u не зависит ни от z, ни от y, то получаем уравнение
— уравнение распространения тепла в стержне.
§2.2. Температурные волны.
Задача о распространении температурных волн в почве является одним из первых примеров приложения математической теории теплопроводности, развитой Фурье, к изучению явлений природы.
Температура на поверхности земли носит, как известно, ярко выраженную суточную и годовую периодичность. Обратимся к задаче о распространении периодических температурных колебаний в почве, которую будем рассматривать как однородное полупространство 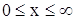
найти ограниченное решение уравнения теплопроводности
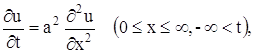
u (0, t) = A cos 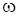
Предполагается, что функции u (x, t) и m (t) ограничены всюду, т.е.
Запишем граничное условие в виде
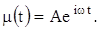
Из линейности уравнения теплопроводности следует, что действительная и мнимая части некоторого комплексного решения уравнения теплопроводности каждая в отдельности удовлетворяет тому же решению.
Если найдено решение уравнения теплопроводности, удовлетворяющее условию (2’), то его действительная часть удовлетворяет условию (2), а мнимая – условию
Итак, рассмотрим задачу:
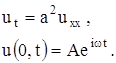
Ее решение будем искать в виде
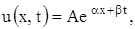
где 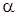
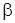
Подставляя выражение (4) в уравнение (3) и граничное условие, находим:
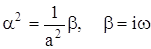
Для u (x, t) имеем:
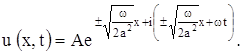
Действительная часть этого решения
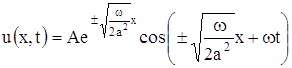
удовлетворяет уравнению теплопроводности и граничному условию (2). Формула (6) в зависимости от выбора знака определяет не одну, а две функции. Однако только функция, соответствующая знаку минус, удовлетворяет требованию ограниченности. Таким образом, решение поставленной задачи получаем в виде
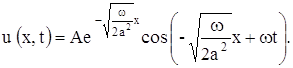
На основании полученного решения можно дать следующую характеристику процесса распространения температурной волны в почве. Если температура поверхности длительное время периодически меняется, то в почве также устанавливаются колебания температуры с тем же периодом, причем:
1.Амплитуда колебаний экспоненционально убывает с глубиной
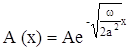
т.е. если глубины растут в арифметической прогрессии, то амплитуды убывают в геометрической прогрессии (первый закон Фурье).
2. Температурные колебания в почве происходят со сдвигом фазы. Время 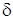
🔍 Видео
8.1 Решение уравнения теплопроводности на отрезкеСкачать

8.2 Теплопроводность на отрезке. Сложные задачи.Скачать

Уравнение в частных производных Уравнение теплопроводностиСкачать

6-1. Уравнение теплопроводностиСкачать

Динамика распространения тепла в стержне.aviСкачать

075 Динамика распространения тепла в стержнеСкачать

075 Динамика распространения тепла в стержнеСкачать

Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать

Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

Физика 075 Динамика распространения тепла в стержнеСкачать

Динамика распространения тепла в стержнеСкачать

Физика 075 Динамика распространения тепла в стержнеСкачать

Динамика распространения тепла в стержнеСкачать

Решение задач теплопроводности (короткая версия)Скачать

Вывод уравнения теплопроводностиСкачать

Физика 075 Динамика распространения тепла в стержнеСкачать

Решение задач теплопроводности (часть 1)Скачать

определение реакций в стержнях от действия грузовСкачать