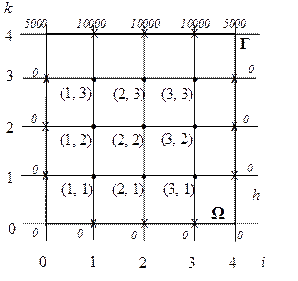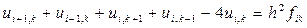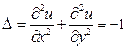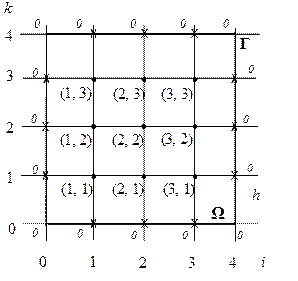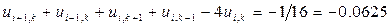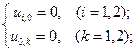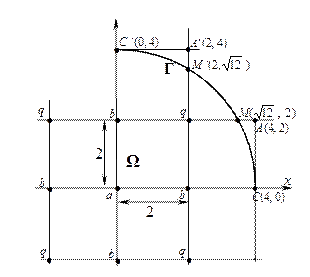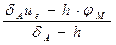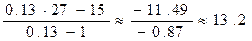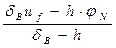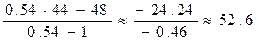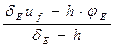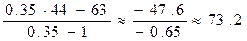Уравнение распределения температуры в пластине (3 видео)

Содержание

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ. Пример 1. Рассмотрим задачу о стационарном распределении тепла в плоской изолированной пластине со стороной 1
Теплопроводность при нестационарном режиме
Лекция№14
💥 Видео

Видео:География 8 класс (Урок№11 - Распределение температуры воздуха по территории России.)Скачать

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ. Пример 1. Рассмотрим задачу о стационарном распределении тепла в плоской изолированной пластине со стороной 1

Пример 1. Рассмотрим задачу о стационарном распределении тепла в плоской изолированной пластине со стороной 1, если на границе пластины поддерживается постоянная температура (указанная на рис. 6) и если известно, что при заданных краевых условиях, функция u(x, y), описывающая распределение температуры в пластине, является решением уравнения Лапласа:

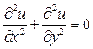
Рисунок 7 – расчётная область с граничными условиями для примера 1

Решение. Для решения задачи построим сетку с шагом 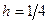. При этом получим девять внутренних узлов (на рис. 6 обозначены точками), в которых необходимо определить значения функции u(x, y). Построенная сеточная область также имеет 12 граничных узлов (на рис. 7 обозначены крестиком), которые лежат на границе Г расчётной области, поэтому значения искомой функции в них определяются из граничных условий.

Далее для полученных внутренних узлов сетки необходимо записать конечно-разностные уравнения для искомой функции u_i_,_k i = 1, 2, 3; k = 1, 2, 3. Однако на данной сетке (как видно из рисунка 7), в силу симметрии граничных условий для значений искомой функции выполняются равенства:

Это сокращает количество неизвестных значений функции u(x, y) во внутренних узлах до шести. Таким образом, в узлах (3, 1), (3, 2), (3, 3) конечно-разностные уравнения писать нет необходимости.

В остальных шести внутренних узлах (1, 1), (2, 1), (1, 2), (2, 2), (1, 3), (2, 3) в соответствии с соотношением (10):

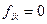
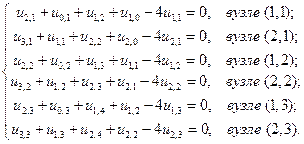
при получаем соответственно шесть уравнений:

(23)

В эти уравнения входят ещё 12 значений функции в граничных точках сетки. И поскольку граничные точки лежат на Г, то значения функции u(x, y) в них мы берём из краевых условий:

(24)

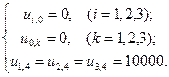
Заметим, что в остальных узлах краевые условия не используются.

Далее учитывая соотношения (22) и (23) из (24) получаем систему уравнений для определения неизвестных значений функции u(x, y) во внутренних узлах:

(25)

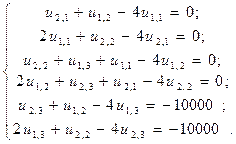
Решив систему (25) методом Гаусса, окончательно получаем

Пример 2. Из теории упругости известно, что задача об упругой деформации квадратной пластины под действием постоянной силы сводится к решению уравнения Пуассона:

с нулевыми краевыми значениями. Найти решение этой задачи методом сеток, приняв сторону квадрата равной 1 и шаг h сетки равным .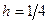

Решение. В данном случае имеет место полная симметрия значений искомой функции, так как все краевые условия краевые, а функция f(x, y) постоянна (рис. 8).

Поэтому конечноразностные уравнения достаточно составить для четверти квадрата, т.е. для узлов (1, 1), (2, 1), (1, 2), (2, 2).

Рисунок 8 – расчётная область с нулевыми граничными условиями для примера 2

В указанных четырёх узлах (1, 1), (2, 1), (1, 2), (2, 2), в соответствии с соотношением (10):

которое для данной задачи имеет вид:

получаем соответственно систему уравнений:

(26)

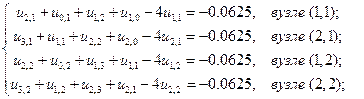
Далее, учитывая нулевые граничные условия:

и что в силу симметрии задачи относительно центра пластины — узел (2, 2):

систему (26) перепишем в виде:

(27)

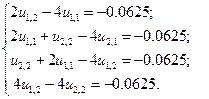
поскольку u₁₂ = u₂₁, то второе и третье уравнения последней системы совпадают, поэтому вместо неё окончательно имеем систему трёх уравнений:

(28)

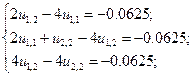
Решив эту систему получаем

Пример 3. Решение краевых задач для криволинейных областей.

Найти приближённое решение уравнения:

, (29)

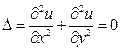
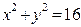
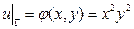
удовлетворяющее на окружности условию:

(30)

Решение. В данном случае границей Г расчётной области является окружность радиуса R = 4, с центром в начале координат. В соответствии с (30) функция j (x, y), задающая значения искомого решения u(x, y) на этой окружности, симметрична относительно начала координат (рис. 9а), поэтому, достаточно найти решение данной краевой задачи на четверти круга.

Будем решать данную задачу поэтапно.

1) На первом этапе возьмём крупную сетку с шагом h = 2 (рис. 9б) и найдём значения координат точек пересечения линий сетки с окружностью (на рис. 9б указанные точки пресечения обозначены соответственно как М и М’ ).

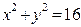
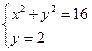
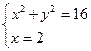
Поскольку точки М и М’ являются точками пересечения окружности и линий сетки, имеющих соответственно уравнения y = 2 и x = 2, то их координаты можно найти решая соответственно системы уравнений:

(31) (32)

Из (31) и (32) соответственно получаем, что точки М и М’ имеют координаты:

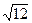
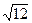
М : x = , y = 2 и М’ : x = 2, y = .

Зная координаты точек М и М’ в соответствии с граничным условием (30) определяем значения решения в точках М и М’.

Для аппроксимации значений искомой функции u(x, y) в граничных узлах сетки А(4, 2) и А’(2, 4) сносим значения решения из точек М и М’ границы Г в точки А(4, 2) и А’(2, 4), т.е. полагаем:

Для граничных узлов С(4, 0) и С’(0, 4), лежащих на границе расчётной области Г, очевидно имеем:

Значения искомого решения u(x, y) во внутренних узлах сетки, которые обозначены на рис. (рис. 9б) буквами a, b, c находим из разностного уравнения:

(11)

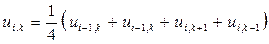
u(a) = ;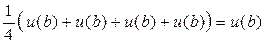

u(b) = ;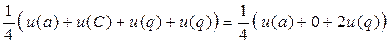

u(q) = .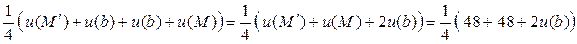

записывая последние равенства более компактно, имеем систему уравнений:

(33)

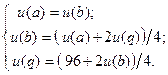
Решая систему уравнений (33) находим:

2) На втором этапе возьмём более мелкую сетку с шагом h = 1 и «грубо» аппроксимируем граничные значения посредством переноса значений с границы области Г в граничные узлы сетки (рис. 9в).

Как и на первом этапе координаты точек пересечения этой сетки с окружностью определяются из следующих систем уравнений:

; ; ; ; ; ;

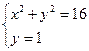
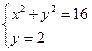
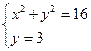
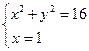
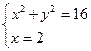
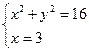
Решая данные системы уравнений, получаем соответственно следующие значения координат точек пересечения линий мелкой сетки и границы Г расчётной области:

( , 1); ( , 2); ( , 3); (1, ); (2, ); (3, );

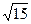
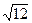
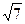
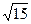
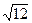
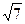
Отсюда в соответствии с граничным условием (30) получаем, что значения искомой функции в точках пересечения линий сетки и границы Г соответственно равны:

15; 48; 63; 15; 48; 63.

Снесём данные значения с границы Г в ближайшие граничные узлы А, А’, В, В’ и С мелкой сетки, в результате будем иметь:

На рис. 9в цифрами узлах сетки обозначены значения искомой функции
u(x, y), вычисленные на предыдущем этапе по крупной сетке, и значения, которые найдены в точках пересечения мелкой сетки и границы Г из граничного условия (30).

Далее используя указанные значения функции u(x, y) найденные на первом этапе в узлах крупной сетки с шагом h = 2 и значения в граничных узлах мелкой сетки, а также учитывая симметрию задачи по формулам:

(11)

(14)

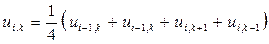
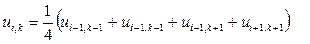
составляем соответственно конечно-разностные уравнения для значений искомой функции u(x, y) в узлах a, b, d, f и q, e:

(34)

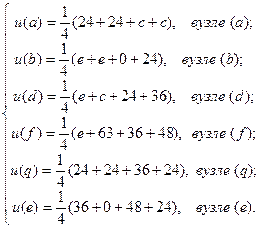
Отметим, что при составлении конечно-разностных уравнений системы (34) для узлов a, b, d, f и q, e использовались шаблоны с разной связью узлов. Решая далее систему уравнений (34) приближённо находим:

3) На третьем этапе уточняем (аппроксимируем) значения искомой функции u(x, y) в граничных узлах А, А’, В, В’ и С используя формулу (17).

Для узла А формула (17) перепишется в виде: u_A =

где d_А = 4 — 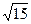» 0.13; h = 1, u(e) = 27; j_M = 15; в результате имеем:

u_A =

Для узла В формула (17) перепишется в виде: u_В =

где d_В = 4 — 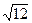» 0.54; h = 1, u( f ) = 44; j _N = 48; в результате имеем:

u_B =

Для узла С формула (17) перепишется в виде: u_С =

где d_Е = 3 — 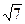» 0.35; h = 1, u( f ) = 44; j _Е = 63; в результате имеем:

u_С =

Таким образом, в граничных узлах имеем: u_A = 13; u_B = 52.6; u_С = 73.2;

Заключение (план — аннотация лекции №28).

В лекции рассмотрена идея метода сеток, или метода конечных разностей, который является одним из распространённых методов численного решения уравнений с частными производными. В основе метода сеток лежит идея замены фигурирующих в уравнении математической физики частных производных конечно-разностными отношениями различной степени точности.

Подробно изложена методика использования метода сеток для решения краевых задач для уравнений эллиптического типа, рассмотрены различные варианты связи узлов в «крестообразных» шаблонах прямоугольных сеток. Приведена оценка погрешности разностного метода решения задачи Дирихле.

Рассмотрена идея аппроксимации граничных условий для решения задачи Дирихле в случае, когда не все граничные узлы сетки лежат на границе расчётной области, в том числе и для случаев построения сеток с «перекрытием» расчётных областей.

На примере третьей краевой задачи для уравнений эллиптического типа обсуждаются подходы, используемые при аппроксимации граничных условий для других граничных условий, встречающихся при решении краевых задач для эллиптического дифференциального уравнения второго порядка.

Приведены примеры решения типовых задач для уравнений эллиптического типа как для случая прямоугольных, так и для случая криволинейных расчётных областей.

1. И.С. Березин, Н.П. Жидков. Методы вычислений. Т. 2. – М.: Физматгиз, 1962. – 620 с.

2. В.М. Вержбицкий. Основы численных методов. – М.: Высшая школа, 2002. – 840 стр.

3. В.Ф. Формалёв, Д.Л. Ревизников. Численные методы. – М.: Физматлит, 2004. 400 с.

4. Б.П. Демидович, И.А. Марон, Э.З. Шувалова. Численные методы анализа.
– М.: Наука, 1967. – 368 с.

5. Н.В. Копчёнова, И.А. Марон. Вычислительная математика в примерах и задачах. – М.: Наука, 1972. – 368 с.

\|	следующая лекция ==>
Постановка задачи для уравнения эллиптического типа	\|	ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ. Пример 1. Используя разностное уравнение (18) найти приближённое решение уравнения теплопроводности:

Дата добавления: 2015-09-14 ; просмотров: 3885 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Закономерности распределения температуры воздуха. География 7 классСкачать

Теплопроводность при нестационарном режиме

Процессы передачи теплоты, в которых температурное поле и поле теплового потока изменяются во времени, называются нестационарными.

Нестационарные тепловые процессы в технике и природе встречаются практически чаще, чем стационарные. Нагрев или охлаждение приборов и машин при пуске, останове или изменении режима; конструктивных элементов зданий и других сооружений при изменении наружной температуры; термическая обработка продуктов и изделий; работа регенеративных теплообменных аппаратов – все это примеры нестационарных тепловых процессов.

Длительность процессов нестационарного конвективного теплообмена и излучения сравнительно мала и не имеет существенного влияния на формирование температурных полей тел в нестационарном режиме, поэтому эти процессы пока мало изучены – их нестационарностью обычно пренебрегают. Процессы же теплопроводности, наоборот, оказывают решающее влияние на формирование температурных полей при нестационарном тепловом состоянии отдельных тел и систем.

Процессы нестационарной теплопроводности можно разделить на две группы: а) нестационарные процессы, связанные с нарушением теплового равновесия, когда с течением времени система стремится к некоторому новому равновесному состоянию; б) нестационарные процессы, связанные с периодическим изменением теплового состояния тела (периодические изменения температуры окружающей среды или мощности тепловых источников и т. п.).

В большинстве задач нестационарной теплопроводности требуется найти температуры в определенных точках тела в заданный момент времени t от начала процесса. Возможна и обратная задача: найти длительность процесса, в результате которого температура в данной точке тела примет определенное, наперед заданное значение. В некоторых задачах бывает необходимо найти тепловой поток в определенной точке в заданный момент времени или полное количество теплоты, отданной (или полученной) телом в течение заданного промежутка времени.

Все перечисленные задачи сводятся к нахождению температуры рассматриваемого тела как функции времени и координат t = f(t, x, у, z).

Эту зависимость можно найти, если проинтегрировать дифференциальное уравнение теплопроводности при заданных краевых условиях.

Для некоторых конкретных задач теплопроводности дифференциальное уравнение может быть упрощено: в случае передачи теплоты в одном направлении задача становится одномерной; при распространении теплоты в двух направлениях задача является двухмерной. Для тел цилиндрической формы удобно перейти к цилиндрическим координатам, а для тел шаровой формы – к сферическим.

Дифференциальное уравнение и краевые условия полностью формулируют задачу. Дальнейшее аналитическое ее решение сводится к использованию методов математической физики. Основные из них: метод разделения переменных, методы интегральных преобразований (например, Лапласа), метод мгновенных точечных источников. Кроме аналитических применяют и приближенные методы.

В качестве примера рассмотрим охлаждение неограниченной пластины.

Охлаждение неограниченной пластины

Будем рассматривать задачу теплопроводности при постоянных значениях теплофизических характеристик тела (l, с,r) с граничными условиями третьего рода, так как они наиболее часто встречаются на практике. Задача формулируется следующим образом. Плоская неограниченная пластина толщиной d, имеющая во всех точках одинаковую начальную температуру t_нч, в момент времени t = 0 помещается в среду, температура которой t_ж 0. Математически задачу можно сформулировать следующим образом. Дифференциальное уравнение теплопроводности для одномерной задачи без внутренних источников теплоты

где х может изменяться в пределах 0 £ х £ d/2: так как охлаждение пластины происходит симметрично, целесообразно поместить начало координат в середину пластины и рассматривать процесс только в одной ее половине (см. рисунок). Краевые условия:

1) начальное условие при t = 0 и 0 £ х £ d/2 t = t_нч;

2) граничные условия: а) при х = 0и t > 0 (дt/дx)₀ = 0, т. к. при симметричном охлаждении в середине пластины в любой момент времени температура будет максимальной; б) при х = l и t > 0 —l(дt/дx)_c = a(t_c – t_ж).

Последнее выражение записано на основании равенства тепловых потоков на поверхности пластины: подходящего к поверхности из внутренних областей тела путем теплопроводности и отводимого от поверхности в процессе теплоотдачи.

Решение задачи в общем виде можно представить как функцию независимых переменных х и t и параметров процесса а,l, a, l, t_ж, t_нч:

Следуя методу подобия, приведем условия задачи к безразмерной форме; это значительно сокращает число переменных, придает полученному решению обобщенность, и упрощает анализ решения.

Для этого произведем сначала замену искомой величины t так называемой избыточной температурой J = t – t_ж.

Так как dJ = dt,то запись дифференциального уравнения и граничных условий от такой замены не изменится:

;

Приведем уравнение и граничные условия к безразмерному виду. Для этого еще раз произведем замену переменных: вместо избыточной температуры введем безразмерную избыточную температуру Q = J/J_нч.Вместо координаты х введем безразмерную координату Х = х/l.Такая замена равносильна тому, что в качестве масштаба для измерения температуры используется величина J_нч, а в качестве масштаба длины – величина l. Для сохранения равенств исходные уравнения в соответствующих местах необходимо умножить на масштабы температуры и длины. Тогда дифференциальное уравнение будет иметь вид:

, или после сокращения и преобразования .

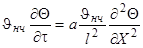
В такой форме дифференциальное уравнение безразмерно: величина l 2 /а имеет размерность времени и потому комплекс аt/l 2 безразмерен. Этот комплекс обозначается символом Fo и называется критерием Фурье:

Критерий Фурье можно трактовать как безразмерное время.

Окончательно дифференциальное уравнение теплопроводности в безразмерной записи получается в следующем виде:

Начальное условие: при Fo = 0, Q_нч = 1;

где Q_с = J_с/J_нч – безразмерная температура поверхности стенки; Bi = al/l – критерий Био.

Физический смысл критерия Био в том, что его величина характеризует соотношение интенсивностей отвода теплоты в процессе теплоотдачи и подвода теплоты из внутренних слоев тела к поверхности в результате теплопроводности.

Теперь искомая функция будет иметь вид Q = f(Fo,Bi, X).

Применяя метод разделения переменных решение дифференциального уравнения будет иметь вид

, (1)

где – коэффициенты уравнения;

m_п – корни характеристического уравнения m/Bi = ctgm.

Значения m_п и А_п приводятся в справочниках.

Результирующее выражение температурной функции, в форме произведения функции времени exp(-m 2 Fo) на некоторую функцию от координаты справедливо не только для пластины, но и для других тел, в которых распространение теплоты происходит в одном направлении, как, например, в бесконечно длинном цилиндре или шаре. Различаются результирующие выражения видом функции координаты: вместо cos – для пластины, для цилиндра появляется функция Бесселя, а для шара – гиперболическая. Для классических тел получены аналитические решения задач нестационарной теплопроводности.

В соответствии с формой результирующих уравнений (1) порядок решения задачи нестационарной теплопроводности для тела классической формы следующий:

1. На основании исходных данных вычисляют безразмерную координату Х и критерии Bi и Fo. Здесь характерный размер тела: для пластины при симметричном охлаждении l = d/2,при одностороннем охлаждении l = d;для бесконечно длинного цилиндра и шара l = R,где R – радиус.

2. По величине критерия Bi в специальных таблицах находят значения m_n и А_п для нескольких значений п.В обычных инженерных расчетах достаточно учитывать два-четыре члена суммы в формуле (1).

3. По формуле (1) или аналогичной ей для тел другой формы вычисляют значение безразмерной температуры Q в данной точке в заданный момент времени. Из Q определяют искомую температуру t = f(t, x).

Анализ решения (1) позволяет выявить влияние величины числа Bi на нестационарную теплопроводность. Рассмотрим два предельных случая: Bi ® ¥ и Bi ® 0.

Первый предельный случай:Bi ® ¥ (практически Bi >100). Для тела конечных размеров (l – конкретная конечная величина) этот случай соответствует условию a/l ® ¥, т. е. большим значениям коэффициента теплоотдачи a и сравнительно малым значениям коэффициента теплопроводности l.В этом случае сразу после начала процесса температура поверхности тела принимает и в дальнейшем сохраняет постоянное значение t_c = t_ж = const. Следовательно, интенсивность процесса охлаждения (нагрева) определяется внутренним процессом теплопроводности в теле и зависит только от физических свойств и размеров тела.

При этом общее решение (1) упрощается: из числа определяющих критериев выпадает критерий Bi. Так, для точек, расположенных в средней плоскости пластины (при Х = 0), уравнение для безразмерной температуры при Fo > 0,3 приобретает вид

Второй предельный случай:Bi ® 0 (практически при Bi 2 ; Bi_пл = al/l; Fo_пл = аt/l 2 .

Величины Q_ц иQ_пл могут быть найдены по графикам с учетом расположения рассматриваемой точки в безграничном теле. Так, для точки 1 (рис.)величина Q_ц находится по графику для центральных точек неограниченного цилиндра, а величина Q_пл – по графику для средней плоскости пластины. Для точки 2величина Q_ц определяется по тому же графику, что и для точки 1, а Q_пл – по графику для поверхностных точек пластины. Для точки 3обе величины находятся по графикам для поверхностных точек цилиндра и пластины. Для точки 4величина Q_ц определяется по графику для поверхностных точек цилиндра, а величина Q_пл – по графику для средней плоскости пластины. Перечисленные четыре точки являются характерными для ограниченного цилиндра. Температуры остальных точек ограниченного цилиндра по графикам не могут быть найдены, но для их определения можно воспользоваться соответствующими формулами.

Аналогичные рассуждения справедливы и для параллелепипеда,но его следует рассматривать как тело, образованное пересечением трех неограниченных пластин.

Регулярный режим охлаждения (нагревания) тел

При значении Fo > 0,3 в выражениях типа (1) достаточно ограничиться одним первым членом ряда. В этом случае для пластины

. (2)

Режим охлаждения (или нагрева), определяемый формулой (2), называется регулярным. Этот результат обобщается и на более сложные задачи охлаждения (нагрева) тел любой геометрической формы при условии t_ж и a = const:

где m – темп охлаждения, [1/с].

В этом случае начальные условия начинают играть второстепенную роль, и процесс полностью определяется только условиями охлаждения на границе тела и среды, физическими свойствами тела, его геометрической формой и размерами.

Логарифмируя последнее уравнение, получаем:

Из последнего уравнения следует, что натуральный логарифм избыточной температуры для всех точек тела изменяется во времени по линейному закону. Если продифференцировать это выражение по времени получим:

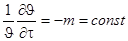
В левой части уравнения стоит выражение для относительной скорости изменения температуры, и оно равняется постоянному значению т,не зависящему ни от координат, ни от времени. Следовательно, темп охлаждения характеризует относительную скорость изменения температуры в теле и зависит только от физических свойств тела, процесса охлаждения на его поверхности, геометрической формы и размеров тела.

Если экспериментально определить изменение избыточной температуры Jво времени t и построить зависимость в полулогарифмических координатах, то темп охлаждения в стадии регулярного режима найдется как

Выражение для зависимости темпа охлаждения т от физических свойств тела, его геометрической формы и размеров, а также условий теплообмена на поверхности тела можно найти из анализа теплового баланса. В результате получим:

где С – полная теплоемкость тела;

y = J_F/J_V – коэффициент неравномерности распределения температуры в теле;

J_F, J_V – средние по поверхности и по объему температуры тела.

Из уравнения следует, что темп охлаждения т, однородного тела при конечном значении коэффициента теплоотдачи a пропорционален коэффициенту теплоотдачи, поверхности тела и обратно пропорционален его теплоемкости (первая теорема Кондратьева ).

Коэффициент y зависит от числа Bi, учитывающего условия протекания процесса на поверхности тела. Рассмотрим два предельных случая:

а) Bi ® 0 (практически Bi 100). При этом условии задача становится внутренней, и процесс охлаждения определяется только размерами тела и его физическими свойствами. В силу большой интенсивности теплообмена температура на поверхности тела принимает постоянное значение, равное температуре окружающей среды. Коэффициент неравномерности распределения температуры y = 0.

При Bi ® ¥, или, что то же, a ® ¥, темп охлаждения т становится прямо пропорциональным коэффициенту температуропроводности тела а (вторая теорема Кондратьева):

Коэффициент пропорциональности К зависит от геометрической формы и размеров тела и определяется в зависимости от формы тела по выражениям:

для шара радиусом r ;

для параллелепипеда с длиной граней l₁, l₂, l₃ ;

для цилиндра длиной l и радиусом r .

На основе теории регулярного режима разработаны различные экспериментальные методики определения теплофизических характеристик материалов.

Видео:Моделирование в задаче определения температурных режимовСкачать

Лекция№14

НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ ТЕПЛОПРОВОДНОСТИ И ИХ ХАРАКТЕРИСТИКИ

Здесь рассматривается перенос теплоты за счет теплопроводности при отсутствии внутренних источников теплоты, когда температура системы изменяется не только от точки к точке, но и с течением времени. Такие процессы теплопроводности, когда поле температуры в теле изменяется не только в пространстве, но и во времени, называют нестационарными. Они имеют место при нагревании (охлаждении) различных заготовок и изделий, производстве стекла, обжиге кирпича, вулканизации резины, пуске и останове различных теплообменных устройств, энергетических агрегатов и т. д.

Среди практических задач нестационарной теплопроводности важнейшее значение имеют две группы процессов: а) тело стремится к тепловому равновесию; б) температура тела претерпевает периодические изменения.

К первой группе относятся процессы прогрева или охлаждения тел, помещенных в среду с заданным тепловым состоянием, например, прогрев болванки в печи, охлаждение металлических брусков, охлаждение закаливаемой детали и т. п.

Ко второй группе относятся процессы в периодически действующих подогревателях, например тепловой процесс регенераторов, насадка которых то нагревается дымовым газами, то охлаждается воздухом. При нагревании однородного твердого тела в среде с постоянной температурой Tж. по мере нагрева температура в каждой точке асимптотически приближается к температуре нагревающей среды. Наиболее быстро изменяется температура точек, лежащих вблизи поверхности тела. С увеличением времени прогрева эта разность будет уменьшаться и теоретически через достаточно большой отрезок времени она будет равна нулю.

В условиях передачи теплоты через стенку при внезапном изменении температуры одного из теплоносителей не вся теплота будет передаваться через стенку: часть ее уйдет на изменение внутренней энергии самой стенки (ее температуры), и только при наступлении стационарного процесса вся теплота будет передаваться через стенку от одной жидкости к другой.

Приведенные примеры указывают на то, что нестационарные тепловые процессы всегда связаны с изменением внутренней энергии или энтальпии вещества.

АНАЛИТИЧЕСКОЕ ОПИСАНИЕ ПРОЦЕССА

Аналитическое описание процесса теплопроводности включает в себя дифференциальное уравнение и условия однозначности.

Дифференциальное уравнение теплопроводности при отсутствии внутренних источников теплоты имеет вид:

(14.1)

Условия однозначности задаются в виде:

(14.2)

Граничные условия могут быть заданы в виде граничных условий третьего рода:

Дифференциальное уравнение теплопроводности (3.1) совместно с условиями однозначности (3.2) дает законченную математическую формулировку рассматриваемой задачи. Решение ее заключается в отыскании функции

(14.3)

Которая удовлетворяла бы уравнению (14.1) и условиям (14.2).

Рассмотрим подробно решение задачи об охлаждении плоской однородной стенки и получим для этого случая конкретный вид функции (14.3). Изучив метод решения задачи для пластины, можно понять принцип решения задач и для тел другой геометрической конфигурации.

ОХЛАЖДЕНИЕ (НАГРЕВАНИЕ) НЕОГРАНИЧЕННОЙ ПЛАСТИНЫ

Постановка задачи. Дана пластина толщиной 2. Если толщина пластины мала по сравнению с длиной и шириной, то такую пластину обычно считают неограниченной.

При заданных граничных условиях коэффициент теплоотдачи одинаков для всех точек поверхности пластины. Изменение температуры происходит только в одном направлении X, в двух других направлениях температура не изменяется (T/Y = /Z = 0), следовательно, в пространстве задача является одномерной. Начальное распределение температуры задано некоторой функцией T(X, 0) = F(X). Охлаждение происходит в среде с постоянной температурой Tж = const. На обеих поверхностях отвод теплоты осуществляется при постоянном во времени коэффициенте теплоотдачи. Отсчет температуры пластины для любого момента времени будем вести от температуры окружающей среды, т. е. T – Tж = . Так как задача в пространстве одномерная, то дифференциальное уравнение (3.1) принимает вид:

(14.4)

(14.5)

При заданных условиях охлаждения задача становится симметричной и начало координат удобно поместить на оси пластины. При этом граничные условия на оси и на поверхности пластины запишутся так:

(14.6)

Дифференциальное уравнение (3.4) совместно с начальным (3.5) и граничными (3.6) условиями однозначно формулируют поставленную задачу.

Решение. Решение дифференциального уравнения (3.4) ищем в виде произведения двух функций, из которых одна является функцией только , а другая – только X (метод разделения переменных):

(14.7)

После подстановки последнего выражения в дифференциальное уравнение (14.4) получим:

В этом уравнении переменные легко разделяются, и его можно записать следующим образом:

(14.8)

Левая часть уравнения (14.8) есть функция только , а правая – функция только X.

Если зафиксировать аргумент X и менять только , то при любом его значении левая часть уравнения (14.8) равна постоянной величине, стоящей в правой части, т. е. ’()/() = const. Аналогично при фиксации  и изменении X правая часть уравнения (14.8) для любого значения X должна равняться постоянной левой части, которая зависит только от , т. е. ”(X)/(X) = const.

Так как равенство (14.8) должно иметь место при любых значениях X и , то обе его части должны быть равны одной и той же постоянной величине. Обозначим последнюю через  и перепишем соотношение (14.8):

Заметим, что нетривиальное решение для функции (X) получаем не при всех значениях , а только при  100). Если число Bi стремится к бесконечности, то температура поверхности пластины сразу становится равной температуре окружающей среды, в которую помещена пластина. Из Bi = (/)/(1/) следует: Bi → ∞ при заданных физических параметрах и толщине пластины тогда, когда  → ∞, т. е. когда имеет место очень большая интенсивность отвода теплоты от поверхности. В этих случаях процесс охлаждения определяется физическими свойствами и размерами тела. При этом , и тогда коэффициент ряда (14.24)

Общее решение для рассматриваемого случая принимает вид:

(14.30)

Тогда температура на оси пластины X = 0

(14.31)

При X = 1 , и, следовательно, X = 1 = 0.

Как было сказано, при Fo ≥ 0,3 ряд (14.24) быстро сходится и ошибка не превышает 1%, если отбросить все члены ряда, кроме первого. При этих условиях уравнение (14.31) принимает вид:

(14.32)

Если уравнение (14.32) прологарифмировать и решить относительно числа Fo, то получим:

(14.33)

Учитывая, что Fo = A/2, уравнение (14.33) можно записать в виде

(14.33′)

По формуле (14.33) можно определить время, необходимое для прогрева середины пластины до заданной температуры.

2. Очень малые числа Bi (практически Bi 100) уравнение (14.39) принимает вид:

(14.40)

Если Bi → 0 (практически Bi 0 и R = 0

Сформулированную задачу решим с помощью разделения переменных, т. е. (R, ) = ()(R). Подставив это выражение в уравнение (14.43), получим два обыкновенных дифференциальных уравнения вида

(14.44)

(14.45)

Из предыдущего параграфа известно, что уравнение (14.44) имеет решение:

(а)

Уравнение (3.45) есть уравнение Бесселя, общий интеграл которого имеет вид:

(б)

Где C2 и C3 – постоянные интегрирования, J0 и Y0 – функции Бесселя первого и второго рода нулевого порядка.

Так как температура на оси цилиндра (R = 0) должна иметь конечное значение, a Y0(0) → ∞, то из физических соображений частное решение уравнения (3.45) не должно содержать бесселеву функцию второго рода и C2 должно быть равно нулю.

С учетом сказанного уравнение (б) принимает вид:

(в)

Если обозначить Kr0 = , тогда частное решение уравнения (3.43) будет иметь вид:

(14.46)

Постоянная  в уравнении (14.46) определяется из граничных условий (R = R0), решение которых приводит к характеристическому уравнению

(14.47)

Здесь J1() – функция Бесселя первого рода первого порядка.

Уравнение (14.47) является трансцендентным, и его удобно решать графическим способом, обозначив: 1/Bi = Y1; J0()/J1() = Y2.

Отметим, что Y2 обращается в нуль в тех точках, для которых J0() = 0.

В тех точках, в которых функция J1() обращается в нуль, функция Y2 претерпевает разрыв непрерывности и становится равной ∞. Функции J0() и J1() являются периодическими затухающими функциями, а кривая Y2 = J0()/J1() напоминает котангенсоиду, но с убывающим периодом. Функция Y1 = /Bi графически представляет прямую линию, проходящую через начало координат. Выполнив построение, в точках пересечения функции Y2 с прямой Y1 получим значения корней характеристического уравнения (14.47). Уравнение (14.47) имеет бесчисленное множество решений, а сами корни, как и для пластины, представляют ряд возрастающих чисел, т. е. 1 100) прямая совпадает с осью абсцисс и корни характеристического уравнения не зависят от Bi, а определяются из условий J0() = 0.

В этом случае процесс охлаждения определяется физическими свойствами тела и его геометрическими размерами. При этом уравнение (14.53) принимает вид:

(14.57)