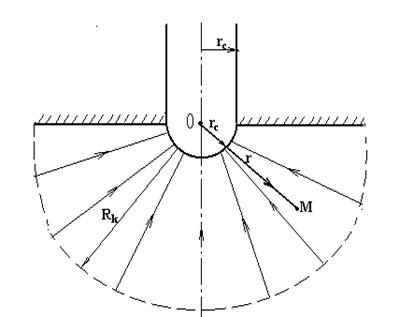
РАДИАЛЬНО- СФЕРИЧЕСКИЙ ФИЛЬТРАЦИОННЫЙ ПОТОК
Фильтрационный поток называется радиально — сферическим, когда прямолинейные пространственные траектории частиц жидкости являются радиально сходящимися в центре одной сферы.
Примером радиально — сферического фильтрационного потока является приток жидкости к скважине, вскрывающей однородный пласт неограниченной толщины у его непроницаемой кровли через полусферический забой, радиус которого равен радиусу скважины (рис.15) .

Рис.15
Рис.16
В этом случае давление и скорость фильтрации в любой точке фильтрационного потока будут функцией только расстояния r этой точки от центра забоя скважины; следовательно, этот вид фильтрационного потока также является одномерным.
Пусть начальное приведенное давление в пласте и на забое скважины равно Рк. Затем на забое давление снизилось до значения Рс = const. Приведенное давление на достаточно удаленной полусферической границе радиуса Rk сохраняется постоянным и равным Rk. В пласте будет иметь место установившийся радиально- сферический фильтрационный поток, описываемый дифференциальным уравнением (3.3).
Для упрощения исследования уравнение Лапласса (3.3) представим в сферических координатах, имея в виду, что Р = Р( r ). Для этого рассмотрим трубку тока с телесным углом j и площадью фильтрационной поверхности w(S) = jr 2 (рис.16). Используя равенства: S = Rk — r ; dS = -dr и закон Дарси, получаем
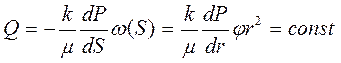
поэтому 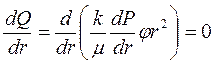
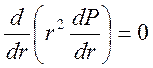
Уравнение (3.32) записываем в развернутом виде
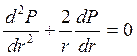
Уравнение (3.33) и есть дифференциальное уравнение Лапласса для радиально- сферического фильтрационного потока.
Дважды последовательно интегрируя уравнение (3.32), находим его общее решение

Постоянные интегрирования С1 и С2 находим по граничным условиям:
при r = R P = Pk = const . (3.35)
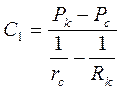

Тогда распределение давления Р=Р( r )получаем из общего решения (3.34) с учетом (3.36)
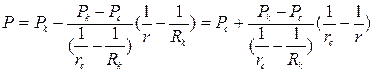

Градиент приведенного давления определяем из выражения (3.34) на основании (3.36)
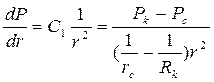
Используя (3.38), находим выражение для дебита добывающей скважины радиусом rc.
Q= 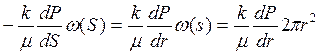

Как видно из (3.39) зависимость Q = Q(DPc) линейная, как и в случае плоскорадиального потока.
Находим выражение скорости фильтрации на расстоянии r от забоя скважины
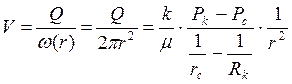
то есть скорость фильтрации V и градиент давления dP/dr в любой точке пласта обратно пропорциональны квадрату расстояния r этой точки до забоя скважины, поэтому график функции dP/dr от r будет более крутым в сравнении с плоскорадиальным потоком.
Аналогичным образом находим закон движения частиц жидкости по траектории.
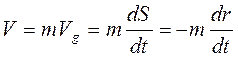
или 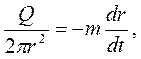
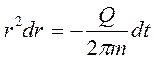
Интегрируя в пределах (0 ¸ t ) и (R0 ¸ r), получаем:
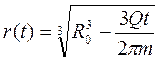
Плоскорадиальный фильтрационный поток
несжимаемой жидкости при нелинейных законах фильтрации
Рассмотрим плоскорадиальный фильтрационный поток несжимаемой жидкости при больших скоростях, когда становятся значительными инерционные составляющие гидравлического сопротивления и линейный закон Дарси нарушается. Для учета инерционных эффектов будем пользоваться степенной (1.25) и двучленной (1.22) зависимостями скорости фильтрации от градиента давления.
Степенной закон фильтрации в условиях плоскорадиального движения имеет вид
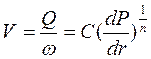
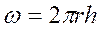
Для определения дебита скважины разделим переменные в (3.42) и проинтегрируем
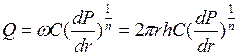
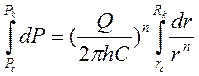

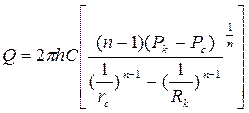
Распределение давления в пласте также определим из уравнения (3.42), проинтегрировав в других пределах:
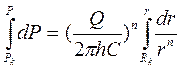
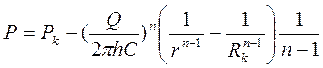
или с учетом (3.43)
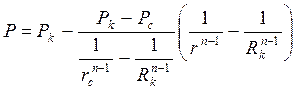
Градиент давления находим по формулам (3.42) и (3.43)
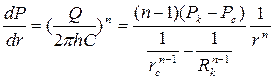
Скорость фильтрации определим из (3.42) с учетом (3.45).
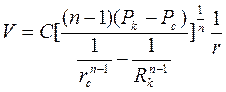
На основании полученных решений (3.43)-(3.46) для значений 1
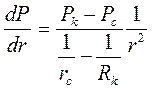
что также совпадает с аналогичной формулой для радиально- сферического потока при линейном законе фильтрации (3.38).
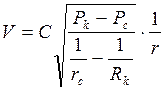
Проанализируем полученные формулы.
Как видно из формулы (3.43) для дебита скважины, индикаторная линия Q = Q(DPc) при 1
Видео:Скин фактор. Влияние параметров работы скважины на ее дебитСкачать

Диагностика газовой скважины по результатам гидродинамических исследований при установившейся фильтрации
Федеральное агентство по образованию
Удмуртский государственный университет
по курсу Подземная гидромеханика
Диагностика газовой скважины по результатам гидродинамических исследований при установившейся фильтрации
1.1 Виды одномерных фильтрационных потоков газа и расчёт основных фазовых характеристик этих потоков
1.2 Методы обработки данных гидродинамических исследований при плоскорадиальной фильтрации
1.3 Приток газа к несовершенной скважине
2. Расчётная часть
2.1. Определение коэффициента фильтрационного сопротивления по данным исследований
2.2. Расчёт теоретических значений коэффициентов фильтрационного сопротивления для гидродинамически совершенной скважины
2.3 Оценка гидродинамического несовершенства скважины
Список используемой литературы
Природный газ является ценнейшим химическим сырьем, из которого получаются самые разнообразные продукты его переработки, использование его в промышленности, помимо огромной экономии в расходовании твердого и жидкого топлива и резкого сокращения перевозок, приводит к интенсификации производственных процессов и меньшему загрязнению окружающей среды. Поэтому, рациональная эксплуатация газовых залежей, базирующаяся на научных исследованиях, является важнейшей задачей газовой отрасли также, как и установление аналитических основ разработки газовых залежей, которые, в свою очередь, строятся на научных теориях движения газа в пористой среде и скважине.
Остановимся на диагностике газовой скважины по результатам гидродинамических исследований при установившейся фильтрации, что включает в себя и исследования и аналитические основы разработки газовых залежей.
Движение газа в скважине нельзя описать линейным законом фильтрации, так как скорость фильтрации зависит нелинейно от градиента давления, что даёт возможность утверждать о движении его по степенному или двучленному закону. Первый из них сложно применить из-за неточности нахождения коэффициентов cи nв данной формуле, что приводит к неточности вычисления скорости фильтрации и давления, поэтому для газовой скважины, в основном, применяют двучленный закон.
Рассмотрим теперь различные виды одномерных фильтрационных потоков, применимых к течению газа, то есть основы течения его по законам прямолинейно-параллельного, плоскорадиального и радиально-сферического фильтрационных потоков.
Выясним, что газ в скважине движется по законам плоскорадиального течения, причём для совершенного случая фильтрации скважина должна быть тоже гидродинамически совершенной, то есть пробуреной на всю мощность пласта и с открытым забоем. Таким образом, изучение гидродинамически несовершенных скважин является ещё одной приоритетной задачей газовой отрасли, такой же, как и приток к таким скважинам газа.
Для изучения всех этих задач вводятся два коэффициента: коэффициент фильтрационного сопротивления и коэффициент гидродинамического несовершенства скважин, которые и рассчитываются по ходу выполнения данной работы, используя формулы, уравнения и графики, взятые из книг различных авторов, изучавших и изучающих гидродинамическое направление течения газа в скважине, хотя для получения более полной картины его течения необходимо применять и геофизические, и геологические исследования, чего в данной работе не сделано, так как это не предусмотрено рамками курсового проекта.
1.1 Виды одномерных фильтрационных потоков газа и расчёт основных фазовых характеристик этих потоков
Одномерным называется фильтрационный поток жидкости или газа, в котором скорость фильтрации, давление и другие характеристики течения являются функциями только одной координаты, отсчитываемой вдоль линии тока. Наиболее характерными, применительно к процессам фильтрации нефти, воды и газа, одномерными потоками являются:
прямолинейно-параллельный фильтрационный поток;
плоскорадиальный фильтрационный поток;
радиально-сферический фильтрационный поток.
Приведем краткое описание этих потоков.
Прямолинейно-параллельный фильтрационный поток. Предположим, что при фильтрации флюида траектории всех частиц параллельны, а скорости фильтрации во всех точках любого поперечно го (перпендикулярного линиям тока) сечения равны друг другу. Законы движения вдоль всех траекторий такого фильтрационного потока одинаковы, а поэтому достаточно изучить движение вдоль одной из траекторий, которую можно принять за ось координат ось x (рис.1).
Прямолинейно-параллельный поток имеет место в лабораторных условиях при движении жидкости или газа через цилиндрический керн или через прямую трубку постоянного диаметра, заполненную пористой средой; на отдельных участках продуктивного пласта при движении жидкости к батарее скважин, если пласт постоянной толщины имеет в плане форму прямоугольника (рис.1).
Рис.1 — Схема прямолинейно-параллельного потока к батарее скважин
Плоскорадиальный фильтрационный поток. Предположим, что имеется горизонтальный пласт постоянной толщины h и неограниченной или ограниченной протяженности. В пласте пробурена одна скважина, вскрывшая его на всю толщину и имеющая открытый забой. При отборе жидкости или газа их частицы будут двигаться по горизонтальным траекториям, радиально сходящимся к скважине. Такой фильтрационный поток называется плоскорадиальным. Картина линий тока в любой горизонтальной плоскости будет одинакова, и для полной характеристики потока достаточно изучить движение флюида в одной горизонтальной плоскости. В плоскорадиальном одномерномпотоке давление и скорость фильтрации в любой точке зависят только от расстояния rданной точки от оси скважины. На рис. 2 а, бприведена схема плоскорадиального фильтрационного потока. Схематизируемый пласт ограничен цилиндрической поверхностью радиусом Rк , (контуром питания), на которой давление постоянно и равно рк ; на цилиндрической поверхности скважины радиусом rс (забой скважины) давление равно рс . Кровля и подошва пласта непроницаемы. На рис. 2,б приведены сечение пласта горизонтальной плоскостью и радиальные линии тока, направленные к скважине. Если скважина не добывающая, а нагнета тельная, то направление линий тока надо изменить на противоположное. Во всех расчётах для плоскорадиального фильтрационного потока dS=-dr.
Рис.2 — Схема плоскорадиального потока в круговом пласте
а-общий вид, б-пласт
Радиально-сферический фильтрационный поток. Рассмотрим схему пласта неограниченной толщины с плоской горизонтальной непроницаемой кровлей. Скважина сообщается с пластом, имеющим форму полусферы радиусом Rк , рис. 3.
Рис.3 — Вертикальное сечение радиально-сферического фильтрационного потока
При эксплуатации такой скважины траектории движения всех частиц жидкости или газа в пласте будут прямолинейными в пространстве и радиально сходящимися в центре полусферического забоя, в точке О. В таком установившемся потоке давление и скорость в любой его точке будут функцией только расстояния rэтой точки от центра полусферы. Следовательно, этот фильтрационный поток является также одномерным и называется радиально-сферическим. Такой поток может реализовываться вблизи забоя, когда скважина вскрывает только самую кровлю пласта или глубина вскрытия h значительно меньше толщины пласта.
Для расчёта перечисленных характеристик одномерных фильтрационных потоков газа можно использовать два подхода. Первый из них вывод дифференциальных уравнений и их решение отдельно для прямолинейно-параллельного, плоскорадиального и радиально-сферического потоков жидкости и газа. Второй-вывод обобщенного уравнения одномерного течения флюида в недеформируемой трубке тока переменного сечения с использованием функции Лейбензона

и получение из него конкретных формул применительно к различным схемам фильтрационных потоков. Второй подход более эффективен, позволяет исходить из обобщенных характеристик течения.
1.2 Методы обработки данных гидродинамических исследований при плоскорадиальной фильтрации
Так как газ в скважине движется по нелинейному закону и движение его плоскорадиальное, то мы можем рассмотреть способ определения основных характеристик потока газа с большими скоростями, когда причиной отклонения от закона Дарси становятся значительные инерционные составляющие общего фильтрационного сопротивления.
Для этого рассмотрим фильтрацию по двучленному закону:
Двучленный закон для плоскорадиальной фильтрации имеет вид:

где β-дополнительная константа пористой среды определяемая экспериментально.
Выразим скорость фильтрации через массовый расход



где Qm — массовый расход 
и подставим в формулу (2)

Разделив переменные и введя функцию Лейбензона(1) получим:

Интегрируя уравнение (5) в пределах от rдо Rк , от рдо рк найдем соответственно:

Приняв в уравнении (6) 

Переходя от функции Лейбензона к давлению по формуле(8) найдём распределение давления:

распределение давления p(r):

где
запишем уравнение притока газа к скважине:

Из формулы(10) видно, что индикаторная линия, построенная в координатах Qатм -( 
Рис.4 – Индикаторная линия при фильтрации газа по двучленному закону
Подставим теперь в уравнение (10) коэффициенты А и В:


Здесь Aи B-коэффициенты фильтрационных сопротивлений, постоянные для данной скважины. Они определяются опытным путем по данным исследования скважины при установившихся режимах.
Скважины исследуются на пяти-шести режимах; на каждом режиме измеряется дебит и. определяется забойное давление. Затем скважину закрывают, и давление на забое остановленной скважины принимают за контурное давление pк . Для интерпретации результатов исследований скважин уравнения (12) делением Qна Qa тм соответственно приводят к уравнению прямой:

График в координатах Qатм -( 
Р ис.5 — двучленному закону . График зависимости ( 
Уравнение притока (12) с экспериментально определен ными коэффициентами широко используется в расчетах при проектиро вании разработки месторождений. Кроме того, по значению А, найденному в результате исследования скважины, можно определить коллекторские свойства пласта, например коэффициент гидропроводности:

Уравнение притока реального газа к скважине по двучленному закону фильтрации имеет вид

где 


Отметим, что в реальных условиях нельзя считать, что во всем пласте -от стенки скважины до контура питания- справедлив единый нелинейный закон фильтрации.
1.3 Приток газа к несовершенной скважине
Виды несовершенства скважин.
Скважина называется гидродинамически совершенной, если она вскрывает продуктивный пласт на всю толщину и забой скважины открытый, т. е. вся вскрытая поверхность забоя является фильтрующей.
Если скважина с открытым забоем вскрывает пласт не на всю толщину h, а только на некоторую глубину b , то ее называют гидродинамически несовершенной по степени вскрытия пласта. При этом 
Если скважина вскрывает пласт до подошвы, но сообщение с пластом происходит только через специальные отверстия в обсадной колонне и цементном камне или через специальные фильтры, то такую скважину называют гидродинамически несовершенной по характеру вскрытия пласта.
Нередко встречаются скважины с двойным видом несовершенства-как по степени, так и по характеру вскрытия пласта.
Степень и характер вскрытия пласта имеют важное значение при разработке месторождений нефти и газа, так как они определяют фильтрационные сопротивления, возникающие в призабойной зоне, и, в конечном итоге, производительность скважин. Выбор степени и характера вскрытия осуществляется в зависимости от физических свойств пластов, их толщины, степени неоднородности, способа разра ботки и т. д. Несовершенство скважин по степени и характеру вскрытия приводит к таким деформациям линий тока, которые приводят к возникновению в призабойной зоне сложных неодномерных течений. В связи с этим рассмотрение особенностей притока к гидродинамически несовершенным скважинам имеет большое практическое значение.
Приток газа к несовершенным скважинам при двучленном законе фильтрации.
Несовершенство газовых скважин при выполнении закона Дарси

учитывается так же, как несовершенство нефтяных скважин, т. е. радиус скважины в формуле дебита заменяется приведенным радиусом:

Для расчета дебитов газовых скважин несовершенных по степени и по характеру вскрытия при нарушении закона Дарси может быть предложена следующая схема. Круговой пласт, в центре которого находится скважина, делится на три области (рис. 6).
Р ис.6 — Схема притока газа к несовершенной по степени и характеру вскрытия скважине
Первая область имеет радиус R1 =(2-3)rс , здесь из-за больших скоростей вблизи перфораци онных отверстий происходит нарушение закона Дарси, т. е. в основном проявляется несовершенство по характеру вскрытия. Линии тока пока заны на рис. 9.
Вторая область представляет собой кольцевое прост ранство R1 ’ — коэффициенты, характеризующие несовершенство скважины по степени вскрытия.



Обе последние формулы-приближенные, они имеют место при значениях b» R1 .
В первой области фильтрация происходит по двучленному закону, плоскорадиальное течение нарушается из-за перфорационных отверстий; несовершенство по характеру вскрытия учитывается коэффициентами С2 и C1 :

Здесь С2 определяется по графикам В. И. Щурова, для С2 ’ предла гается приближенная формула

где N — суммарное число перфорационных отверстий; ℓ ’ -глубина проникновения перфорационной пули в пласт.
Складывая почленно уравнения (22), (24)и(27) и пренебрегая величиной 1/R2 , получим уравнение притока газа к несовершенной скважине в виде

Если записать уравнение (29) через коэффициенты фильтрационных сопротивлений Аи Bв виде (12), то для несовершенной скважины получим:

где C1 и C1 ’ определяются по формулам (25) и (26), С’2 -по формуле (28), а С2 -по графикам В. И. Щурова(рис.10).
Рис. 10 — Графики В. И. Щурова для определения коэффициента С2 при ℓ= 0,5.
Номерам кривых соответствуют значения α: 1 -_0,02; 2 — 0,04; 3 — 0,06; 4 — 0,08; 5 — 0,1; 6 — 0.1; 7 — 0,14; 8 — 0,16; 9 — 0,18; 10 — 0,2
2.1 Определение коэффициента фильтрационного сопротивления по данным исследований.
| pзаб , МПа | Qат , м³/сут |
| 1,5 | 124000 |
| 1,6 | 76000 |
| 1,6 | 36000 |
| 1,66 | 14000 |
В ходе проведения исследований были установлены следующие значения для забойного давления(pзаб ) и дебита скважины(Qат ),
Взяв за основу эти pзаб и переведя Qиз куб. метров в сутки в куб.метры в секунду(таб.2), а также зная тот факт, что при Q=0 pзаб =pпл , то есть при дебите скважины равном 0 забойное давление равно пластовому, можем найти пластовое давление, построив график зависимости между забойным давлением и дебитом скважины(рис.11)
| pзаб , МПа | Qат , м³/с |
| 1,5 | 1,435185185 |
| 1,6 | 0,87962963 |
| 1,6 | 0,416666667 |
| 1,66 | 0,162037037 |
Рис.11 — Зависимость между пластовым давлением и дебитом скважины
Из этого рисунка видно, что при исследованиях была допущена ошибка в измерении pзаб. и соответствующего ему дебита, а именно при pзаб =1,6 МПа дебит скважины, в данном случае, не равен Qат ≠0.416666667 м 3 /с.
Исключая это значение и продолжая график до пересечения с осью Y, когда Qат =0 построим новый график зависимости между забойным давлением и дебитом скважины (рис.12) и найдем из него pпл .
Рис.12 — Зависимость между квадратом пластового давления и дебитом скважины
Видим, что пластовое давление равно 
Теперь, зная, что пластовое давление =1,73 МПа и фильтрация происходит по двучленному закону построим графикзависимости ( 
(  )/Q ат , МПа 2 *с/м 3 )/Q ат , МПа 2 *с/м 3 | Q ат , м 3 /с |
| 0,515679 | 1,435185185 |
| 0,488636 | 0,87962963 |
Рис. 13 — Графикзависимости ( 
А и В – коэффициенты фильтрационного сопротивления.
Коэффициент А находим, как расстояние между осью абсцисс и точкой пересечения прямой с осью ординат, а коэффициент B, как тангенс угла наклона прямой к оси абсцисс, то есть B=tgβ.
Из теоремы о нахождении тангенса угла в прямоугольном треугольнике знаем, что он равен отношению противолежащего катета к
прилежащему поэтому
Коэффициент Aв свою очередь равен: 
2.2 Расчёт теоретических значений коэффициентов фильтрационного сопротивления для гидродинамически совершенной скважины
В расчетах были использованы следующие исходные данные:
| Название параметра | Обозначение | Значение |
| Мощность пласта, м | h | 30 |
| Глубина вскрытия, м | b | 15 |
| Проницаемость, 10 -12 м 2 | k | 0,29 |
| Радиус контура питания, м | Rк | 300 |
| Радиус скважины, м | rс | 0,08 |
| Атмосферное давление, 10 6 Па | pат | 0,1 |
| Атмосферная температура, К | Тат | 293 |
| Плотность при pат и Тат , кг/м 3 | ρат | 1,967 |
| Динамическая вязкость нефти, мПа*с | μ | 0,012 |
| Коэффициент сверхсжимаемости | z | 0.72 |
| Пластовая температура, К | Тпл | 301 |
| Доп. коэффициент пористой среды | β | 15 |
По формуле для двучленной фильтрации совершенной скважины получаем:

где
Найдём коэффициент гидродинамического сопротивления А:
Коэффициент гидродинамического сопротивления В равен:
Введя коэффициенты несовершенства скважины по степени вскрытия С1 и С1 ’ получим двучленную фильтрацию для несовершенной скважины.
С1 и С1 ’ находим по формулам (25) и (26) соответственно.
Зная С1 и С1 ’ , а также степень вскрытия пласта 
2.3 Оценка гидродинамического несовершенства скважины
Зная теперь значения коэффициентов А и В для совершенных и несовершенных скважин можем найти несовершенство скважины.
Оно записывается в виде:

Qсов и Qнесов находим из уравнения(31),взяв 

0,003· 

D=(0,27) 2 -4·0,003·(-0,74)=0,08178

0,011· 


Из этого следует:
Если выразить 

Выразим δ по следующей формуле:


1.По данным гидродинамических исследований газовой скважины был построен график зависимости забойного давления(pзаб )от дебита(Q) из которого, исключив неправильное значение pзаб , было найдено пластовое давление(pпл ) методом экстраполяции этой кривой до пересечения с осью ординат, а также коэффициенты гидродинамического сопротивления А и В, путём построения графика зависимости ( 
2.По формулам двучленной фильтрации были вычислены коэффициенты гидродинамического сопротивления А и В для совершенной скважины, причём при сравнении их с коэффициентами Ан и Вн , вычисленными по тем же формулам для несовершенной скважины, выяснилось, что извилистость каналов фильтрации оказывает большее влияние на течение жидкости, чем её вязкость, т.е. ΔB> ΔA.
3.Зная значения коэффициентов гидродинамического сопротивления А и В и то что скважины эксплуатировались при одинаковых условиях нашли несовершенство скважины, причём и по отношению дебитов Qи Qат , и по отношению коэффициентов А и Ан оно практически одинаково и отличается лишь на 1% , что может быть связано с неточность подсчётов.
4. Вычисленные теоретически и практически для несовершенной скважины коэффициенты гидродинамического сопротивления А одинаковы, в отличии от коэффициентов В, которые отличаются почти в 5 раз, это связано с тем, что оценка извилистости каналов фильтрации по известным давлениям и дебитам менее точна, чем та же оценка по известным фильтрационным характеристикам пласта. 4.
Список используемой литературы
1. Басниев К.С., Кочина И.Н., Максимов В.М. Подземная гидромеханика. М.: Недра, 1993г.
2. Ш. К. Гиматудинов Физика нефтяного и газового пласта М.: Недра, 1971г.
Видео:Задача 5 Определить дебит нефтянной скважины в случае установившейся плоскорадиальной фильтрацииСкачать

Плоскорадиальный поток (приток к скважине)
Рис. 2.3  . Схема притока к скважине . Схема притока к скважине |
Пусть в горизонтальном пласте постоянной толщины h и проницаемости k происходит фильтрация несжимаемой жидкости с вязкостью m к совершенной скважине радиусом rc, на которой поддерживается давление рс. На расстоянии Rk от скважины находится круговой контур питания, на котором поддерживается давление рk. (Рис. 2.3). Направим ось координат 0r от скважины. Для полного исследования такого потока, как было выяснено ранее, достаточно изучить движение жидкости вдоль оси 0r. Площадь поперечного сечения на радиусе r представляет боковую поверхность цилиндра и равна ω = 2 π r h . Математическая постановка задачи описывается следующими уравнениями.
Уравнение неразрывности потока, которое при фильтрации несжимаемой жидкости удобно записать в интегральной форме:
 | (2.17) |
Законом фильтрации — законом Дарси. Так, как фильтрация происходит против направления оси 0r, то скорости фильтрации, а соответственно и расходы будут отрицательными. Поэтому в законе Дарси опустим знак минус.
 | (2.18) |
А также граничными условиями
 | (2.19) |
Требуется найти распределение давления по пласту и дебит скважины.
Для решения полученной задачи подставим закон Дарси в уравнение неразрывности. Тогда получим дифференциальное уравнение первого порядка, которое легко интегрируется:
 | (2.20) |
Из граничного условия на контуре питания получим:
 | (2.21) |
Для исключения постоянной интегрирования ‘c’ вычтем из уравнения (2.16) уравнение (2.15). При этом воспользуемся свойством логарифмов ln(Rk) ‑ ln(r) = ln(Rk/r).
 | (2.22) |
Тогда распределение давления по пласту запишется
 | (2.23) |
Откуда видно, что давление в пласте при плоскопараллельной фильтрации меняется по логарифмическому закону. Используя второе граничное условие, найдем дебит скважины
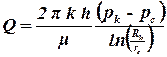 . . | (2.24) |
Формулой для распределения давления (2.23) удобно пользоваться, если известно давление на контуре и дебит скважины. Если известны давления на контуре и на скважине удобнее из формулы (2.24) исключить расход
 . . | (2.25) |
При известных значениях давления на скважине и дебите получим
 | (2.26) |
Скорость фильтрации можно найти или по закону Дарси, или используя уравнение неразрывности потока
 | (2.27) |
Из последнего выражения видно, что скорость фильтрации уменьшается обратно пропорционально расстоянию от скважины.
Рис. 2.4  . Распределение давления a) и отношение скорости фильтрации в пласте к скорости фильтрации на скважине б) для нефтяной скважины . Распределение давления a) и отношение скорости фильтрации в пласте к скорости фильтрации на скважине б) для нефтяной скважины |
Найдем время вытеснения нефти водой при постоянном расходе галереи от контура питания до расстояния r. Считая вытеснение поршневым, получим, что за время t скважина добудет объем нефти Q t. А из пласта будет отобран объем нефти, которая находилась в порах пласта p (Rk 2 — r 2 ) h m. Так, как это объемы одинаковы, то:
 | (2.28) |
Полное время вытеснения нефти при поршневом вытеснении получим, если в последнюю формулу подставим r = rc.
🎥 Видео
Гидроразрыв пластаСкачать

Видеопрезентация гидравлического разрыва пластаСкачать

20. С.В. Головин. Моделирование гидроразрыва пласта: теория и экспериментСкачать

Воп.–Отв. №17."Как рассчитать давление на контуре питания на любом расстоянии от забоя скважины"Скачать

Гидроразрыв пласта, анимационный роликСкачать

Испытание пласта на приемистость LOT. Управление скважиной при бурении.Скачать

Вопрос – Ответ №5.Пласт.Скин-фактор (ГРП, ПВР, кислотная обработка). Псевдоскин-фактор / Skin factorСкачать

Противовыбросовые и плашечные превенторы. Управление скважиной.Скачать

Многостадийный гидроразрыв пластаСкачать

Физика пласта. Основные параметры пластов коллекторовСкачать

Компоновка для МГРП с применением муфт, активируемых шарамиСкачать

Делитель потока на гидравлику. Как сделать одновременное выдвижение гидроцилиндров.Скачать

КАК ДЕЛАЮТ Гидроразрыв ПластаСкачать

Логические элементы "И", "ИЛИ" в системах пневмоавтоматикиСкачать

Гидрострелка. Принцип работы. Сравнение с байпасом. Как правильно подключить.Скачать

Оборудование для ГРП. Гидроразрыв пласта. Добыча нефти и газа.Скачать

Вскрытие продуктивных пластовСкачать

Причины обводнения продукции скважины их идентификация и технологии ликвидации. Изоляционные работы.Скачать