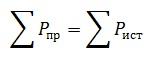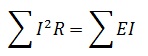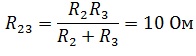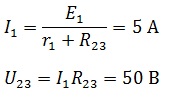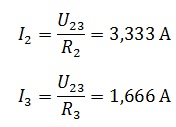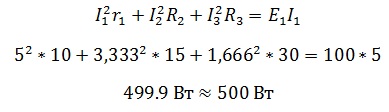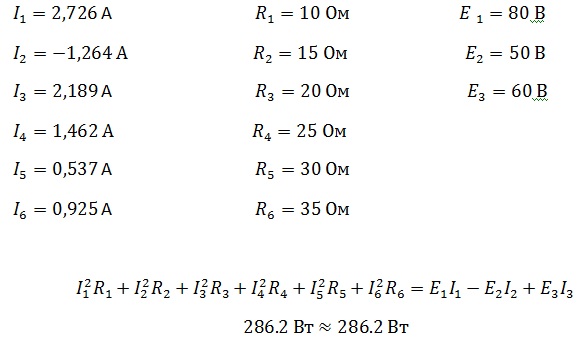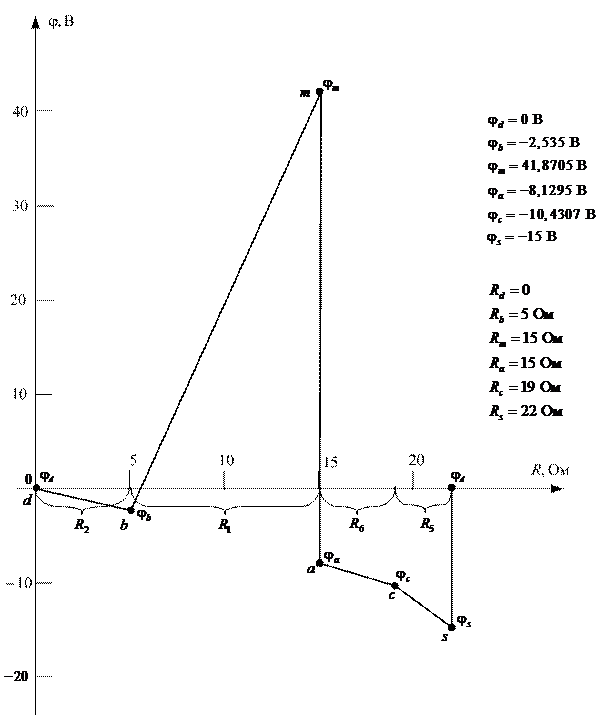Уравнение распределения мощности в цепи (8 видео)

Баланс мощностей электрической цепи

Электрическая цепь предполагает передачу определенной мощности от источника к потребителю. При этом, должно сохраняться равновесие, если схема состоит из сопротивлений, индуктивности. Статья раскроет тему, что такое баланс мощностей в простой цепи переменного тока. Будет описан этот показатель для постоянного напряжения, приведены формулы вычисления.

Содержание

Определение
Назначение
Переменный ток
Постоянный ток
Заключение
Видео по теме
Уравнение распределения мощности в цепи
Баланс мощностей с источником тока
Похожие статьи:
7 thoughts on “Баланс мощностей в цепи постоянного тока”
💡 Видео

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Определение

Вычисление данного параметра в электрической цепи основано на известном законе сохранения энергии. Из него следует, что мгновенные показатели, передаваемые от источника, должны быть равны сумме значений, которую получают потребители.

Баланс для мощностей представляет собой общеизвестный нам закон сохранения энергии. Выражение данного закона в этом случае — сумма всей энергии от источников (генератора или блока питания) равняется сумме, которую получают приемники.

Можно использовать альтернативный вариант. Для него формула при этом имеет вид как на рисунке ниже:

Стоит принять во внимание, что любая электрическая схема имеет сопротивление. Описываемая величина с сопутствующими значениями рассчитывается с учетом разновидности напряжений. Принимая во внимание закон сохранения энергии, стоит учитывать, что по электрической схеме всегда передается энергия.

Видео:Реактивная мощность за 5 минут простыми словами. Четкий #энерголикбезСкачать

Назначение

Составление простого баланса мощностей используют для точного определения расхождений между передаваемой и получаемой энергиями. Также, уравнение баланса мощностей применяется для решения многих электротехнических задач.

Видео:8 класс, 21 урок, Расчет электрических цепейСкачать

Переменный ток

Баланс мощностей в простой цепи переменного тока рассчитывается по более сложной формуле. Баланс мощностей в простой цепи синусоидального тока учитывает комплексные, реактивные и активные параметры.

Комплексная. Состоит из мощностей передаваемых и получаемых. Необходимо будет выполнить расчет, в котором все слагаемые левой части формулы являются положительными (идут со знаками +), при условии, когда совпадает направление заряженных частиц «Ik» с «ЭДС». Должно соблюдаться правило не совпадения «Jk» с направлением напряжения «Uk». Если условия не соответствуют установленным требованиям, все данные левой части формулы становятся отрицательными. Формула приведена ниже.
Активные. Значения, отдающиеся источником равны принимаемым потребителями. Вычисление активной мощности полностью зависит от представленной комплексной энергии. Активное значение является расходуемым, невосполнимым, так как уходит на работу приборов. Данный метод вычисления и его формула представлены ниже.
Реактивная мощность источника с потребителем равны. Единственное отличие заключается в том, что этот параметр не растрачиваемый. Данный показатель просто циркулирует по схеме. Формула представлена ниже.

Главное отличие рассматриваемой величины — это наличие ненаправленного движения переменного тока по проводникам. Параметр такой схемы может быть увеличен или уменьшен (например, генератором), что может повлиять на конечный результат.

Видео:Урок 363. Мощность в цепи переменного токаСкачать

Постоянный ток

В электрической цепи постоянного тока напряжение и мощность всегда одного значения. Поэтому сделать вычисление намного проще. Можно сделать расчет на основе достаточно простого примера.

В цепи имеется ЭДС «Е» и резистор «R». При расчете должна быть найдена сила тока.
I=E/R. Подставляем имеющиеся значения, получаем I=10/10=1 ампер.
Так мы нашли силу тока. Теперь нам будет нужен параметр мощности приемника «R» и источника.
Pист=I×E=1×10=10 Ватт. Это значение для источника.
Теперь для того, чтобы найти Р для приемника делаем расчет как на рисунке ниже.
Теперь составим общий баланс — 10 ватт=10 ватт. Данный подсчет показал, что для представленной схемы сохраняется равновесие.

При вычислении параметров этой схемы имеет смысл учесть расход приемника. Резистор при нагреве выделяет тепло, а значит выполняется преобразование электричества в тепло. Беря во внимание физический закон сохранения, тепло выделяемое резистором также будет равно 10 Ватт.

Видео:RLC цепь│Задача. Определить ток, напряжения и мощности в цепиСкачать

Заключение

В статье было приведено описание, способ расчета баланса мощностей для постоянного и переменного тока. Для электротехники данный баланс очень важен, ведь с помощью него можно выполнять различные расчеты.

Видео:Баланс мощностейСкачать

Видео по теме

Видео:Распределение потенциалов в электрической цепиСкачать

Уравнение распределения мощности в цепи

В любой электрической цепи должен соблюдаться энергетический баланс — баланс мощностей: алгебраическая сумма мощностей всех источников равна арифметической сумме мощностей всех приемников энергии.

В левой части равенства слагаемое берется со знаком «+» если Е и I совпадают по направлению и со знаком «-» если не совпадают.

Если направления ЭДС и тока I в источнике противоположны, то физически это означает, что данный источник работает в режиме потребителя.

Видео:Мощность в цепи переменного тока. 11 класс.Скачать

Баланс мощностей с источником тока

При решений электротехнических задач, часто нужно проверить правильность найденных значений. Для этого в науке ТОЭ, существует так называемый баланс мощностей.

Баланс мощностей – это выражение закона сохранения энергии, в электрической цепи. Определение баланса мощностей звучит так: сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками. То есть если источник ЭДС в цепи отдает 100 Вт, то приемники в этой цепи потребляют ровно такую же мощность.

Или

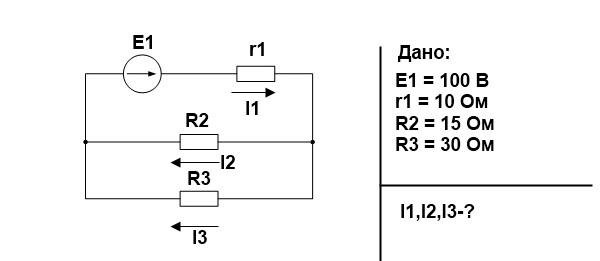
Проверим это соотношение на простом примере.

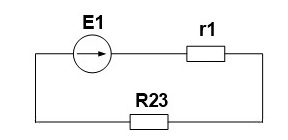
Для начала свернем схему и найдем эквивалентное сопротивление. R2 и R3 соединены параллельно.

Найдем по закону Ома ток источника и напряжение на R₂₃, учитывая, что r₁ и R₂₃ соединены последовательно, следовательно, сила тока одинаковая.

Теперь проверим правильность с помощью баланса мощностей.

Небольшое различие в значениях связано с округлениями в ходе расчета.

С помощью баланса мощностей, можно проверить не только простую цепь, но и сложную. Давайте проверим сложную цепь из статьи метод контурных токов.

Как видите независимо от сложности цепи, баланс сошелся, и должен сойтись в любой цепи!

Баланс мощностей в электрической цепи означает, что мощность, которую выделяют все источники энергии, равна мощности, которую потребляют в этой же цепи все приемники энергии:

, (2.69)

где – мощность i-го источника ЭДС или тока, Вт; – мощность, выделяемая в j-м сопротивлении, Вт.

Очевидно, что баланс мощностей следует из закона сохранения энергии.

Запишем для анализируемой цепи рис. 2.15 сумму мощностей, выделяемых всеми источниками энергии. При этом мощности, выделяемые источниками ЭДС и тока, будем считать положительными, если ток в ветви, где установлен источник ЭДС или тока, совпадает с направлением тока внутри источника (со стрелкой в обозначении источника ЭДС или тока), и отрицательными, если направление тока в ветви противоположно направлению тока в источнике. Тогда, составив соответствующее уравнение для вычисления суммарной мощности, отдаваемой источниками ЭДС и тока в анализируемую цепь и подставив в него численные значения, получим суммарную мощность источников:

[Вт]. (2.70)

при этом токи ветвей должны подставляться в уравнение (2.70) со своим знаком, который получился при их расчете.

Суммарная мощность, рассеиваемая в цепи сопротивлениями (приемниками энергии), для той же цепи рис. 2.15, может быть найдена так:

[Вт]. (2.71)

В результате расчета (2.70) – выделяемая источниками мощность, и (2.71) – потребляемая сопротивлениями мощность в цепи – должны быть одинаковы.

Потенциальная диаграмма электрической цепи

Постоянного тока

Потенциальная диаграмма контура электрической цепи постоянного тока – это графическое изображение второго закона Кирхгофа, в котором вместо падений напряжений записаны потенциалы узлов электрической цепи. Она показывает суммарное значение потенциала и суммарное сопротивление в данной точке цепи того контура, для которого построена диаграмма, считая от опорного узла, потенциал которого принят за нулевой. Иными словами, потенциальная диаграмма показывает распределение потенциалов и сопротивлений в том контуре цепи, для которого она построена.

Графически эта диаграмма представляет собой ломаную линию, изображенную в декартовой системе координат, горизонтальной осью которой (осью абсцисс) является ось сопротивлений , а вертикальной осью (осью ординат) – ось потенциалов .

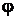
Процесс построения потенциальной диаграммы электрической цепи рассмотрим для той же, что и ранее, электрической цепи, показанной на рис. 2.3, и модифицированной для удобства построения потенциальной диаграммы так, как показано на рис. 2.15.

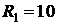
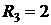
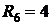
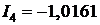
Поскольку для построения потенциальной диаграммы требуется знание численных значений токов ветвей и сопротивлений ветвей, приведем эти численные значения для цепи рис. 2.15 при условии, что исходные данные для расчета этой цепи таковы: Ом, Ом, Ом, Ом, Ом, Ом; величины источников ЭДС: В, В; величины источников тока: А, А. Значения токов в ветвях цепи, рассчитанные прямым применением законов Кирхгофа (сам расчет здесь не приводится), таковы: [А]; [А]; [А]; [А]; [А]; [А].

Построение потенциальной диаграммы начнем с выбора контура, для которого эта диаграмма будет составляться. На наш взгляд, наиболее информативно будет построить потенциальную диаграмму для контура d-b-m-a-c-s-d, так как в этом контуре содержатся все источники ЭДС и источники тока анализируемой цепи и при таком обходе на потенциальной диаграмме будут показаны потенциалы всех узлов анализируемой схемы. Далее произведем выбор опорного узла, потенциал которого примем за ноль. Есть смысл взять за опорный узел d, как и ранее при расчетах анализируемой цепи. Потенциал этого узла положим равным нулю, как и ранее (2.44).

Определим численные значения потенциалов узлов и точек анализируемой схемы, находящихся на пути обхода выбранного нами контура d-b-m-a-c-s-d. Поскольку потенциал узла d равен нулю (2.44), то потенциал узла b определится так:

[В]. (2.72)

Знак «плюс» при произведении означает, что потенциал узла b повышается при переходе от узла d анализируемой схемы к узлу b (см. полярность падения напряжения на сопротивлении от тока на схеме рис. 2.15).

Следующим определим потенциал точки m анализируемой схемы:

[В]. (2.73)

Знаки при произведениях и соответствуют полярностям, показанным на схеме рис. 2.15.

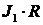
Следующим за точкой m анализируемой схемы идет узел a. Его потенциал равен:

[В]. (2.74)

Рис. 2.15. Эквивалентная схема анализируемой электрической цепи для построения потенциальной диаграммы

Далее определим потенциал узла c, значение которого составит:

[В]. (2.75)

Потенциал 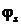точки s, следующей за узлом c по выбранному нами обходу, равен:

[В]. (2.76)

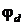
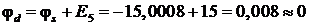
Обойдя таким образом весь контур d-b-m-a-c-s-d, мы возвращаемся в узел d. При этом потенциал узла d должен стать равным нулю. В самом деле, так оно и происходит, так как при подходе из узла c к узлу d, потенциал последнего станет равен:

[В]. (2.77)

После расчета численных значений потенциалов для контура d-b-m-a-c-s-d можно построить саму потенциальную диаграмму. Эта диаграмма показана на рис. 2.16.

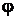
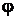
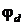
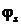
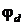
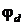
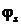
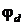
Техника построения потенциальной диаграммы такова. На осях декартовой системы координат откладывают значения потенциалов и сопротивлений для контура цепи (схемы), который был ранее выбран для построения потенциальной диаграммы. В нашем примере, рис. 2.15, это контур d-b-m-a-c-s-d. Значения заранее рассчитанных величин потенциалов для каждой из точек этого контура откладывают на вертикальной оси (оси ординат) в положительную или отрицательную область значений, в зависимости от знака потенциала, полученного ранее при расчете. В нашем примере это будут потенциалы , , , , , и вновь точек d-b-m-a-c-s-d, соответственно. Порядок следования значений потенциалов в потенциальной диаграмме соответствует их порядку при расчете значений потенциалов. В анализируемой нами цепи рис. 2.15, этот порядок , , , , , , соответствует обходу контура d-b-m-a-c-s-d. Значения сопротивлений откладываются по горизонтальной оси (оси абсцисс) декартовой системы координат. За нулевое (исходное) значение сопротивления в потенциальной диаграмме принимается значение в опорном узле; в нашем примере рис. 2.15 это значение сопротивления в узле d. Далее, по мере обхода контура цепи, который выбран для построения потенциальной диаграммы (в нашем примере это контур d-b-m-a-c-s-d), значения сопротивлений в каждой последующей точке прибавляются к значениям сопротивлений в предыдущей точке.

Таким образом, сопротивление в каждой точке потенциальной диаграммы контура оказывается суммарным для этой точки, начиная с опорного узла, где значение сопротивления принято за ноль. Если при переходе из одной точки контура в другую сопротивления в схеме цепи нет, то к предыдущему значению сопротивления прибавляется ноль (это имеет место при прохождении источника ЭДС с нулевым внутренним сопротивлением).

Рис. 2.8.2 Потенциальная диаграмма контура d-b-m-a-c-s-d исследуемой цепи

В нашем примере значения сопротивлений в точках потенциальной диаграммы контура d-b-m-a-c-s-d составят:

[Ом]. (2.78)

Таким образом, при построении потенциальной диаграммы контура электрической цепи по вертикальной оси декартовой системы координат откладывают потенциалы узлов по мере их упоминания при обходе контура, а по горизонтальной оси – нарастающим итогом сопротивления также по мере их упоминания при таком обходе. Используют потенциальную диаграмму цепи для наглядного визуального представления распределения потенциалов и соответствующих им сопротивлений по тому или иному контуру электрической цепи.

Библиографический список

1. Основы теории цепей. Методические указания и контрольные задания для студентов радиотехнического факультета спец. 0701 “Радиотехника”.-Сост. Ю.А.Мантейфельд, А.Д.Суслов. М.: МИРЭА.-1980.-48 с.

2. Основы теории цепей. Методические указания по выполнению расчетно-графических заданий №1-2 для студентов радиотехнического факультета. Сост. В.И.Вепринцев. Красноярск: Изд-во КГТУ, 2000. 64 с.

3. Шебес, М.Р., Каблукова, М.В. Задачник по теории линейных электрических цепей: Учеб. пособ. для электротехнич., радиотехнич. Спец. вузов.-4-е изд. перераб. и доп.-М.: Высш. шк., 1990.-544 с.: ил.

4. Основы теории цепей: учебник для вузов / Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. – 5-е изд., перераб. – М.: Энергоатомиздат, 1989. – 528 с.

5. Теория линейных электрических цепей: учебник для вузов / Б.П.Афанасьев, О.Е.Гольдин, И.Г.Кляцкин, Г.Я.Пинес. – М.: Высш. шк., 1973. – 592 с.

Оглавление

1. ЗАДАНИЕ И ВЫБОР ВАРИАНТА ДЛЯ ЕГО ВЫПОЛНЕНИЯ.. 4

2. РАСЧЕТ ВЕЛИЧИН ТОКОВ НЕПОСРЕДСТВЕННЫМ ПРИМЕНЕНИЕМ ЗАКОНОВ КИРХГОФА, МЕТОДАМИ КОНТУРНЫХ ТОКОВ, УЗЛОВЫХ ПОТЕНЦИАЛОВ И МЕТОДОМ ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА.. 9

2.2. Анализ (расчет) сложных электрических цепей. 19

методом контурных токов. 19

2.6.3 Анализ (расчет) сложных электрических цепей. 25

методом узловых потенциалов. 25

2.6.4 Анализ (расчет) сложных электрических цепей. 31

методом эквивалентного генератора. 31

2.5. Баланс мощностей в электрической цепи постоянного тока. 40

2.6 Потенциальная диаграмма электрической цепи. 41

постоянного тока. 41

Библиографический список. 47

Дата добавления: 2018-02-15 ; просмотров: 2258 ; ЗАКАЗАТЬ РАБОТУ

Баланс мощностей является следствием закона сохранения энергии — суммарная мощность вырабатываемая (генерируемая) источниками электрической энергии равна сумме мощностей потребляемой в цепи.

Источники E1 и E2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадают (если ЭДС и ток в ветвях направлены в противоположную сторону, то источник ЭДС потребляет энергию и его записывают со знаком минус). Баланс мощностей для заданной цепи запишется так:

С учетом погрешности расчетов баланс мощностей получился.

7 thoughts on “Баланс мощностей в цепи постоянного тока”

Блин все ошибки найдут, в условии должно быть Е1 = 20, Е2 = 30.
P.S. Сейчас исправлю, спасибо за внимательность

Какова допустимая погрешность?? У меня выходит 0,561

По идее баланс мощности должен равняться нулю, но так как мы округляем некоторые значения при расчете — возникает погрешность, которая может составлять примерно 0,1 — 5% от потребляемой мощности.

Про знаки ЭДС сказано про знаки мощностей приёмников — нет.