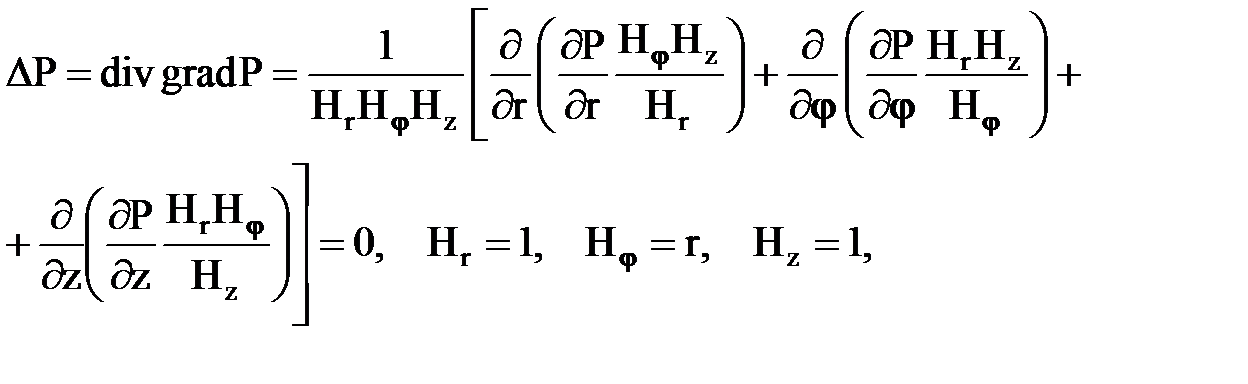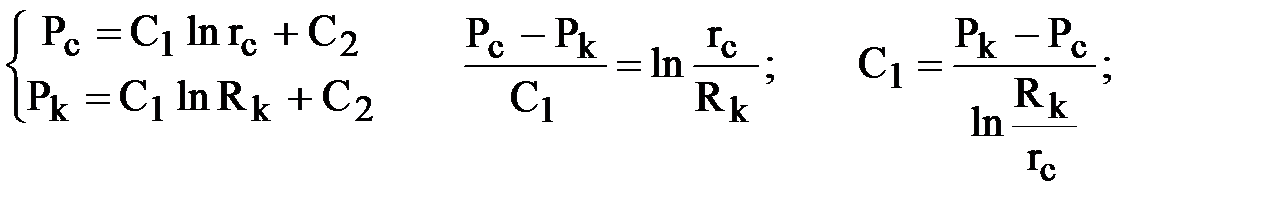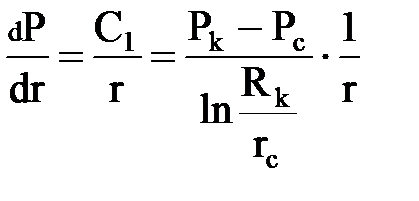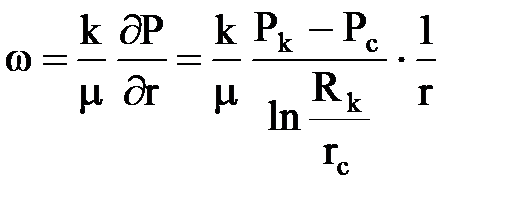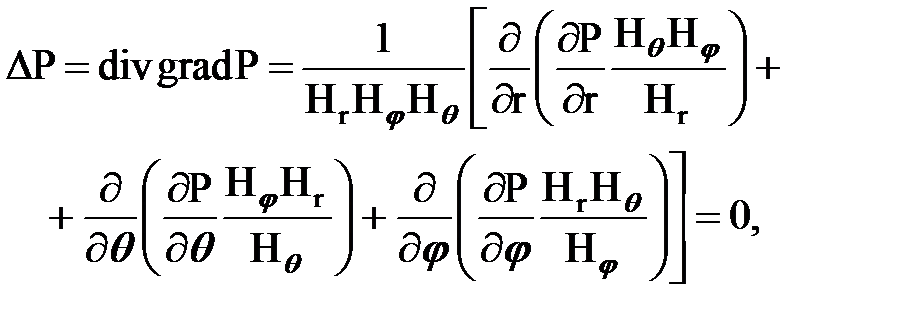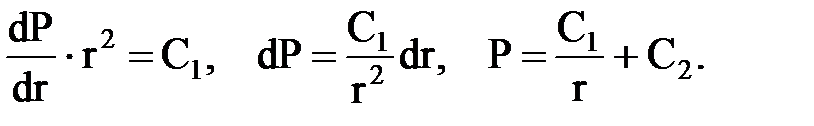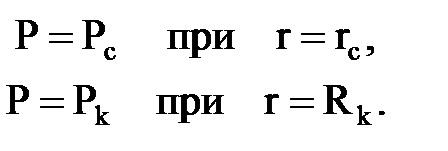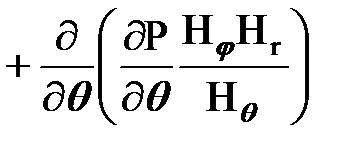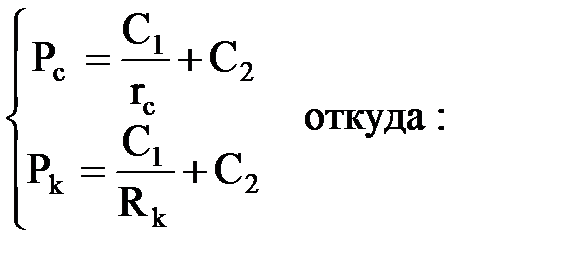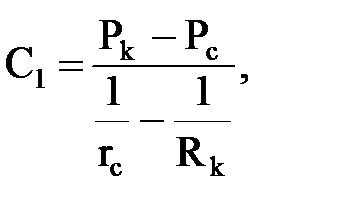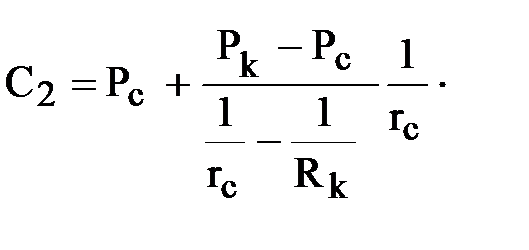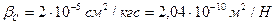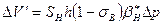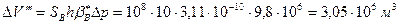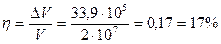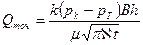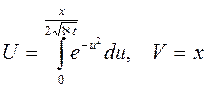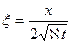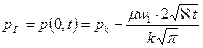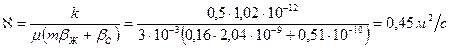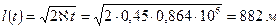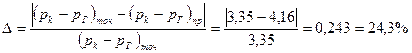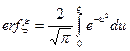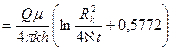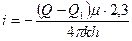Глава 6
ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ
ПРИ РАСЧЁТАХ РАЗРАБОТКИ
В практических задачах моделирования процессов разработки нефтяных и газовых месторождений получение точных и даже приближённых решений оказывается весьма затруднительным, а в ряде случаев и невозможным. Причины тому сложная конфигурация месторождений; неоднородность по площади и разрезу; тектонические нарушения геологической структуры и др. Приведённые ранее решения некоторых задач используются для качественных и количественных оценок интегральных показателей разработки при проектировании и оценки использования тех или иных систем разработки.
Модель разработки нефтяного месторождения обычно представляется математически в виде системы, состоящей из алгебраических, дифференциальных, интегральных уравнений или соотношений. Для того чтобы провести расчёт на основе уже созданной модели разработки месторождения, необходимо сначала решить соответствующие математические задачи. Только получив решение этих задач, можно осуществлять сам расчёт в цифрах. Точные оценки поведения залежи в процессе разработки осуществляется с помощью ЭВМ на основе численных методов решения задач фильтрации.
Методы получения точных решений задач
Математической физики
Многие задачи разработки нефтяных и газовых месторождений сводятся к решению классических уравнений математической физики. В ряде случаев можно получать решения задач математической физики, в точности удовлетворяющие исходным уравнениям, начальным и граничным условиям. Такие решения называются точными. К числу методов, дающих точные решения задач разработки нефтяных месторождений, относится хорошо известный из курса математики метод разделения переменных (метод Фурье), методы функций комплексного переменного, интегральных преобразований, получения автомодельных решений и др.
Методы функций комплексного переменного являются классическими методами решения задач установившейся фильтрации несжимаемой жидкости в плоских пластах. Рассмотрим эти методы при установившемся притоке жидкости к источникам (скважинам).
1. Уравнение неразрывности массы жидкости, фильтрующейся в плоском пласте, имеет, исходя из (4.12), следующий вид:

Подставляя в это уравнение формулу закона Дарси


получаем уравнение Лапласа
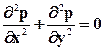
Введем потенциал фильтрации в виде

В этом случае вместо уравнения (6.3) получим
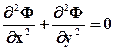
Введем комплексный потенциал
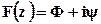

Входящая в выражение (6.5) функция 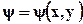



Таким образом, любая аналитическая функция комплексного переменного 

Допустим, что в неограниченном плоском пласте (рисунок 6.1) по оси х располагается бесконечная цепочка источников (скважин). Каждая из скважин находится на расстоянии 2s от соседней. Для того чтобы найти решение задачи о течении жидкости в пласте, достаточно рассмотреть течение жидкости только в одной полосе шириной 2а, расположенной по обе стороны от оси у.
Получить формулу притока жидкости к одному источнику можно было бы путем суммирования бесконечного числа решений для источников, расположенных на расстояниях 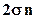




При конформном преобразовании, осуществляемом функцией (6.7), любой точке полосы 
Можно с достаточным приближением считать, что вместо точечного источника в плоскости z существует скважина радиусом rс, где потенциал равен Фс. Тогда примем, что на расстоянии rк от центра скважины потенциал равен Фк. Для дебита скважины в плоскости zможно написать формулу Дюпюи

Если перейти к некоторой плоскости z, то при больших значениях у течение в полосе 
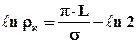
При значительных расстояниях по оси у имеем 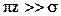
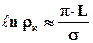
При незначительных
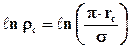
Подставляя приведённые значения 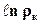

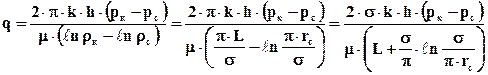
По формуле (6.9) можно определить дебит одной скважины из бесконечной цепочки скважин, расположенных в неограниченном пласте, при условии, что на некотором, достаточно большом расстоянии z от оси х давление равно рк, а в скважинах малого радиуса rс оно составляет рс.


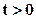
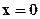

Будем исходить из уравнения сохранения энергии, рассматривая теплоперенос в стержне только за счёт теплопроводности. Для скорости теплопереноса uт за счёт теплопроводности имеем следующее уравнение:
Рисунок 6.2 – Схема распространения температуры за счёт теплопроводности в полубесконечном стержне: 1 – полубесконечный стержень площадью сечения S; 2 – распределение температуры в стержне в момент времени t
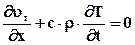
где с – удельная теплоемкость вещества в стержне; r – плотность вещества.
Скорость переноса тепла uт за счёт теплопроводности можно определить по формуле закона Фурье

где lт – коэффициент теплопроводности.
Подставляя (6.11) в (6.10), получаем
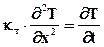
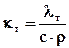
Уравнение (6.12) есть уравнение теплопроводности при прямолинейном распространении тепла, а входящий в него коэффициент kт называется коэффициентом температуропроводности. В соответствии с условиями задачи
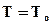
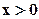

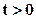


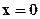
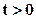
Рассмотрим функцию 
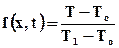
Тогда начальное и граничное условия (6.13) запишутся следующим образом:

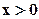

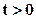

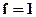
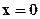
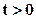
Функция 

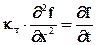
Для получения решения рассматриваемой задачи применим преобразование Лапласа. В результате получим выражение для скорости переноса тепла на границе 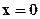


Поток тепла qт через течение стержня площадью S при

3. Рассмотрим приток жидкости (нефти) с постоянным дебитом q к точечному стоку, расположенному в однородном бесконечно простирающемся плоском пласте толщиной h при упругом режиме. Сток находится в центре координат, и течение к нему в пласте радиальное. В начальный момент времени 
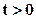


Уравнение неразрывности массы фильтрующегося в пласте вещества имеет в рассматриваемом случае следующий вид:

Учитывая закон Дарси и сжимаемость пласта (сжимаемость пород пласта и насыщающей их жидкости), из (6.19) получаем уравнение упругого режима в следующем виде:

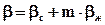
где bс и bж – сжимаемость соответственно пород пласта и насыщающей пласт жидкости. Остальные обозначения такие же, что и принятые выше в формуле закона Дарси. Введём функцию 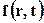

и подставим ее в уравнение (6.11). В результате получим

Здесь k – пьезопроводность пласта. Поскольку сток точечный ( 

Следовательно, граничное и начальное условия будут


Известно, что рассматриваемое решение задачи зависит от одной переменной 
Приближённые методы
Из приближённых методов расчёта в теории разработки нефтяных месторождений наиболее распространены метод эквивалентных фильтрационных сопротивлений Ю.П. Борисова и метод интегральных соотношений Г.И. Баренблатта. Первый из указанных методов используют при расчёте установившихся течений жидкостей в плоских пластах со скважинами, а второй – в расчётах перераспределения давления жидкости при упругом режиме, неустановившегося движения газа и реже – задач диффузии, теплопроводности и конвекции. Метод интегральных соотношений хорошо разработан только для решения одномерных задач.
Рассмотрим вначале метод эквивалентных фильтрационных сопротивлений. Справедливость этого метода можно показать на примере конкретного решения о притоке жидкости к бесконечной цепочке скважин. Так, перепишем формулу (6.9) следующим образом:
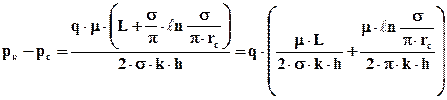
Первый член выражения, стоящего в скобках (6.24), характеризует фильтрационное сопротивление при движении жидкости в полосе шириной 2а на расстоянии от 0 до L, а второй член – фильтрационное сопротивление при радиальном движении жидкости от кругового контура 


Метод эквивалентных фильтрационных сопротивлений позволяет рассчитывать с достаточной для практики точностью дебиты и давления в пластах при различных системах разработки.
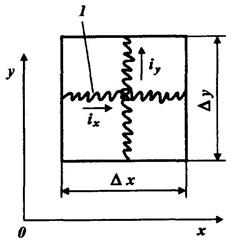
Рассмотрим однорядную систему разработки со схемой расположения скважин, показанной на рисунке 6.3. При этом происходит поршневое вытеснение нефти водой из пласта толщиной h. Вязкость нефти в пластовых условиях составляет mн, а вязкость воды mв. Абсолютная проницаемость пласта k, а относительные проницаемости для нефти и воды, являющиеся постоянными согласно модели поршневого вытеснения нефти водой, равны соответственно kни kв,радиус добывающей скважины rс, радиус нагнетательной скважины rнс. Вода в процессе вытеснения нефти в момент времени 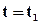
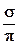

ходу одной нагнетательной скважины, постоянен и составляет q. Требуется определить перепад давления между нагнетательной и добывающей скважинами.
Рассмотрим течение в одном элементе пласта (рисунок 6.3, заштрихованный квадрат) шириной 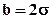
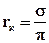
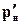
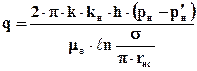
Согласно методу эквивалентных фильтрационных сопротивлений течение в рассматриваемом элементе складывается из трёх: радиального (течение воды) от нагнетательной скважины радиусом rнс до контура радиусом 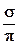
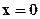
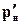
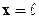



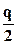
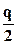
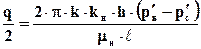
Наконец, для дебита добывающей скважины имеем формулу
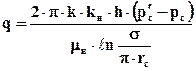
Перепишем приведённые выше выражения относительно перепадов давлений в виде



Сложим эти выражения. В результате получим требующийся ответ

Рассмотрим ту же задачу, что и (6.12) – (6.13), но решим ее методом интегральных соотношений Г.И. Баренблатта, согласно которому приближённое решение задачи представляется в виде многочлена. Далее считаем, что приближённое распределение температуры удовлетворяет не исходному дифференциальному уравнению, а интегральным соотношениям, получаемым в результате умножения левой и правой частей уравнения на координату в степени n и их интегрирования. При использовании описываемого приближённого метода принимают, что всякое незначительное изменение температуры в случае теплопроводности или давления в случае упругого режима распространяется не мгновенно, а существует в ограниченной «возмущённой» области. Для рассматриваемой задачи интегральное соотношение имеет вид
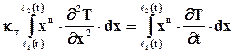
где n – любое, обычно целое число, начиная с нуля. Положим в качестве первого приближения 
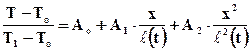
Выполним граничные и начальное условия, которые при приближённом решении задачи имеют несколько иной вид, чем при точном решении, а именно:
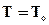
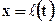
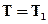
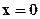
Должно также всегда выполняться условие 

Соблюдая приведённые условия, получаем
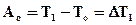

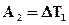

Для определения 



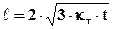
т.е. задача решена.
Определим, как и в примере 2, скорость уноса тепла при 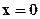

Сравнивая приведённое приближённое выражение с точным (6.18), находим, что скорость уноса тепла, определенная приближённым методом, будет больше точной в 
Численные методы
Основным численным методом, используемым в разработке, является конечно-разностный метод решения дифференциальных уравнений в частных производных, для которого имеется большое количество программ для ЭВМ, разработанных в различных институтах (ВНИИ, ОАО «БашНИПИнефть», ОАО «РосНИПИтермнефть» и др.) и отечественных и зарубежных фирмах (ЮКОС, Лукойл, Shell и др.).
В современных расчётах разработки реальных нефтяных месторождений чаще всего применяют конечно-разностные методы. При использовании этих методов дифференциальные уравнения, описывающие процессы разработки нефтяных месторождений, представляют в конечно-разностной форме. Конечно-раз-ностные уравнения решают с помощью быстродействующих электронно-вычисли-тельных машин-компьютеров. Удобные для использования точные решения задач разработки нефтяных месторождений практически обычно получают только для одномерных случаев (прямолинейное и радиальное течения). При необходимости же рассчитать процессы разработки пластов с учётом их сложной геометрической формы, получить точные и даже приближённые решения не удается. В таких случаях решить задачу можно, применяя численные методы.
Хотелось бы отметить, что решение дифференциальных уравнений в частных производных можно назвать целой областью математики, которую необходимо изучать несколько лет, и поэтому полученные в этом разделе сведения носят весьма ограниченный характер. Однако он должен дать возможность ориентироваться при использовании программ для ЭВМ при численном решении задач фильтрации.
Например, пусть задана некоторая конфигурация месторождения (рассматривается двумерный случай) (рисунок 6.4). При 


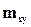



Необходимо рассчитать перераспределение давления в области со сложной конфигурацией при упругом режиме с момента пуска первой скважины до некоторого момента времени и определить продвижение границы водонефтяного контакта (ВНК).
Вот такая очень упрощенная задача, в которой не учитывается пространственная неоднородность, не учитывается смешение нефти и вытесняющей ее воды, не принимается различие пласта по мощности по площади месторождения, не учитывается качество вскрытия пластов в каждой скважине и многое другое. Современные программы для ЭВМ позволяют решать гораздо более сложные задачи.
Основой численных методов решения дифференциальных уравнений в частных производных являются:
1) дискретизация области и выбор сетки решения (плоской и пространственной);
2) замена уравнений на соответствующие разностные операторы;
3) составление системы алгебраических уравнений согласно математической постановке задачи (вид уравнения и граничные условия);
4) численное решение системы алгебраических уравнений (по шагам времени и по «молекулам»);
5) оценка устойчивости решений.
Дискретизация области подразумевает её разбиение с помощью сеток. Для плоскости сетки представляют собой
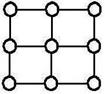 | 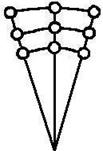 |
| прямоугольная | полярная |
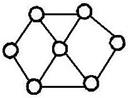 | 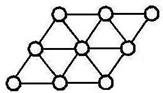 |
| треугольная |
Эти сетки выбираются с целью наилучшего приближения к границам или чтобы повысить точность вычисления в какой-либо интересующей области.
В зависимости от вида сетки записываются и конечно-разностные операторы (часто называют молекулы, так как их изображают в виде строгих формул), которые заменяют соответствующие дифференциальные операторы
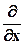

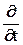

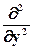
Для примера будем рассматривать прямоугольную сетку 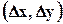
В этом двумерном случае уравнение упругого режима имеет вид

Область течения нефти в плоском пласте разбивается на множество ячеек с размерами Dх, Dу и h соответственно по осям х, у и z. Рассмотрим ячейку А, которая при бесконечном дроблении ( 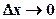



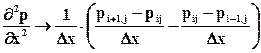
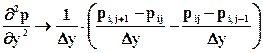
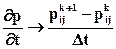
Подставляя (6.33) в дифференциальное уравнение (6.32), получаем
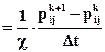
Здесь 
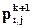
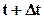
Граничные и начальные условия при решении задач численными методами также приводят к соответствующей конечно-разностной форме. Соотношение (6.34) представляет собой алгебраическое уравнение. Таким образом, при использовании конечно-разностных методов вместо дифференциальных решают алгебраические уравнения.
Последнее соотношение представляет собой алгебраическое уравнение. Подобные соотношения можно составить для каждой ячейки, двигаясь по узлам сетки.
Граничные и начальные условия при решении задач численными методами также приводят к соответствующей конечно-разностной форме. Учёт граничных условий состоит в том, что если в узел попадает граница, то значение функции на границе попадает в молекулу, а если пересечение сетки с границей не в узле, то используются специальные аппроксимационные молекулы. Схематично это можно проиллюстрировать на следующем рисунке.
Методы решения соответствуют методам решения больших систем алгебраических уравнений, разработанных в специальных разделах математики.
Устойчивость решения – это воспроизводимость его при разных путях решения, используемых молекул и методов решения алгебраических уравнений, шаге сетки и шаге времени.
Так, для уравнения пьезопроводности
при 
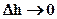
и тогда погрешность вычислений будет порядка h 2 .
Это, в принципе, все те немногие сведения и примеры, которые достаточно знать для того, чтобы представлять, что такое численные методы и как они могут использоваться при решении задач разработки месторождений.
Аналоговые методы
Одним из методов решения задач теории фильтрации при разработке месторождений является метод аналогового моделирования. Его основой является математическая аналогия записи основных моделей разных процессов. Согласно закону Ома, для силы тока ix и iy в направлениях х и у имеем выражения

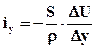
где S – площадь поперечного сечения электрического проводника; r – удельное электрическое сопротивление; DU – приращение электрического напряжения.
Сравним выражения (6.35) с формулой закона Дарси, представленной в конечно-разностной форме. Имеем


Выражения (6.35) и (6.36) совпадают, если давление жидкости заменить электрическим напряжением, скорости фильтрации – силой электрического тока, a 



Следовательно, если написать
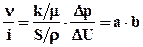


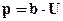
где а и b – коэффициенты пропорциональности, которые позволяют, проводя измерения тока и напряжения, получить соответствующие параметры фильтрации.
В случае двумерной фильтрации имеем аналоговую ячейку.
Рисунок 6.5 – Ячейка А: 1 – электрические сопротивления
В случае упругого режима аналогом коэффициента сжимаемости пласта b является электрическая емкость С. Можно записать:


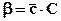
где а, b и с – коэффициенты пропорциональности.

и уравнение пьезопроводности можно записать в виде


Следовательно, собрав соответствующую электрическую цепь для ячейки пласта с соответствующими k и m сопротивлениями и конденсаторами между ячейками, получим электрогидродинамическую аналогию (ЭГДА) поля пьезопроводности.
Процессы, описываемые уравнением (6.40), можно моделировать на специальных устройствах, называемых электроинтеграторами, подключая к каждой ячейке соответствующие электрические сопротивления и электрические емкости. По формулам (6.39) проводим пересчёт электрических параметров, экспериментально определяемых на электроинтеграторах, на соответствующие фильтрационные параметры. Электроинтеграторы позволяют моделировать задачу пьезопроводности. При этом граничные и начальные условия моделируются для давлений в виде напряжений, а потоки – в виде токов.
В настоящее время в связи со стремительным ростом производительности и объёмов памяти ЭВМ ЭГДА используют достаточно редко, так как для больших размеров и широкого диапазона вариации свойств создание ЭГДА весьма трудоёмко и дорого.
Модель пласта с модифицированными относительными
Проницаемостями
Относительные проницаемости – важнейшие характеристики, определяющие внутрипластовые потоки нефти, воды и газа, а, следовательно, обводненность продукции, текущую и конечную нефтеотдачу пластов.
Исходные измерения относительных проницаемостей производят на лабораторных установках путем осуществления фильтрации соответствующих флюидов через образцы пород пласта. Однако эти измерения относительных проницаемостей производятся на выбуренных из пласта образцах пород, имеющих, естественно, небольшие размеры. Так, диаметры и длины образцов цилиндрической формы составляют всего несколько сантиметров. При компьютерных расчётах разработки пластов приходится использовать конечно-разностные ячейки размером по площади пласта 
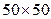
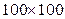
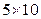
Видео:Методы поддержания пластового давленияСкачать

Одномерные фильтрационные потоки несжимаемой жидкости в однородном пласте
Одномерным называется фильтрационный поток жидкости, в котором скорость фильтрации и напор являются функциями только одной координаты, отсчитываемой вдоль линии тока.
К одномерным относятся следующие потоки.
1. Прямолинейно-параллельный фильтрационный поток.
Контур питания для одной скважины – это условный контур, окружающий скважину, за пределами которого можно пренебречь возмущающим влиянием добывающей скважины. Для одиночной скважины – таким контуром является окружность такого радиуса, при котором на ней Р = Рпл = Pk и w = 0. Для прямолинейной батареи скважины контур питания (условия на котором Р = Рk и w = 0 сохраняются) также становится прямолинейным.
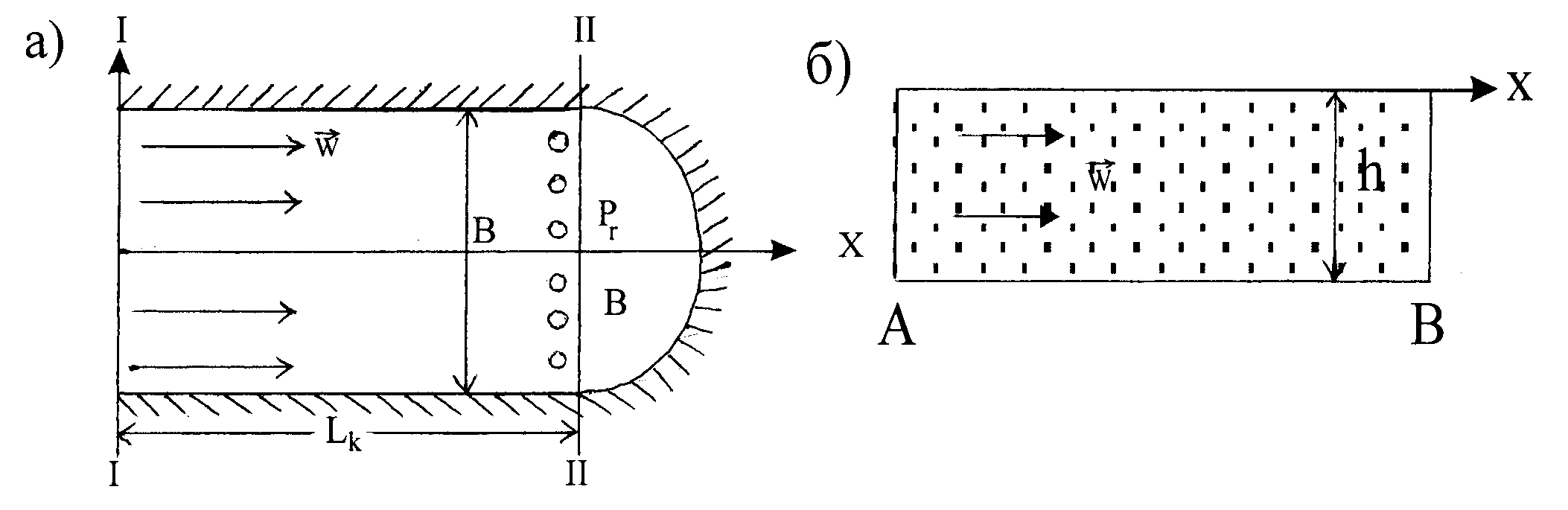
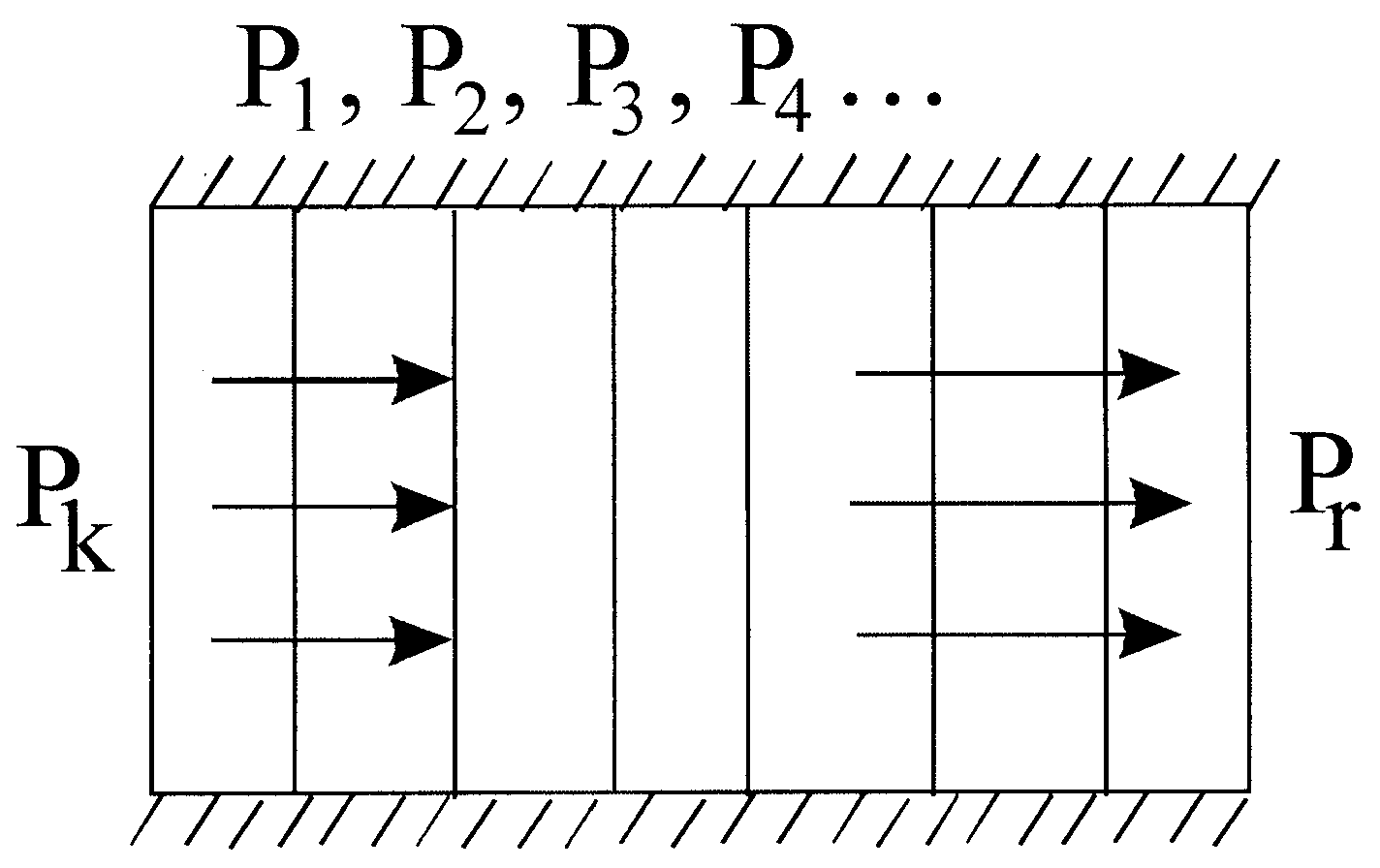
Для прямолинейно-параллельного фильтрационного потока линии тока жидкости в плане пласта и в его продольном сечении являются прямыми линиями, а скорость v в любой точке вертикального сечения пласта одинакова. Такой фильтрационный поток возникает при эксплуатации однородного пласта прямоугольной формы, у которого на контуре питания поддерживается постоянным давление Рк, а батарея скважин, у которых давление на забое Рr, расположена параллельно контуру питания (рис.10.1).
 |
 |
Рис. 10.1 План модели (а) и разрез по линии OX (б)
Условныеия обозначения: — линии тока жидкости; — батарея (галерея) добывающих скважин; I-I – контур питания; II-II – линия размещения батареи скважин; В – ширина разрабатываемого месторождения (зоны); Lk – расстояние от контура питания до батареи скважин; h – мощность пласта; v- вектор скорости фильтрации
2. ) Плоскорадиальный параллельный фильтрационный поток.
Особенность плоскорадиального потока заключается в том, что линии тока совпадают с радиусами, сходящимися к центру окружности (скважине) и находятся в одной плоскости. В любом горизонтальном сечении пласта поведение линий тока одинаково. Плоскорадиальный поток создается в однородном круговом пласте постоянной мощности или пласте
неограниченной протяжности, если в центре него пробурена скважина, вскрывшая пласт на всю мощность и имеющая открытый ствол (рис. 10.2 и 10.3).
| Рис. 10.3 Линии тока жидкости в вертикальном сечении пласта. |
| w |
| скважина |
| rk, Pc |
| Rk, Pk |
| r |
| Рис. 10.2 Линии тока жидкости в пласте. |
1) Радиально-сферический фильт
3. Радиально-сферический фильтрационный поток.
Линии тока этого потока сходятся к центру сферы. Такой поток будет в пласте неограниченной мощности, вскрытом скважиной, имеющей полусферический забой (рис. 10.4).
Описанные три вида фильтрационных потоков являются простейшими моделями реальных течений, возникающих при разработке месторождений и играющих важную роль для практических расчетов.
Задача исследования заключается в определении гидродинамических характеристик: дебита (или расхода), давления, grad P и скорости фильтрации в каждой точке пласта, а также в установлении закона движения частиц вдоль их траекторий, и определения средневзвешенного по объему порового пространства пластового давления.
3.5.1. Прямолинейно-параллельный фильтрационный поток.
Пусть в горизонтальном пласте толщины h и ширины В в сечении I-I, совпадающем с контуром питания, поддерживается постоянное давление Рк, а в сечении II-II, отстоящем на Lк, поддерживается давление Рr в батарее добывающих скважин (рис. 10.1).
Дифференциальное уравнение Лапласа для такого течения: 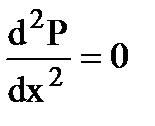
Интегрируя дважды, имеем:
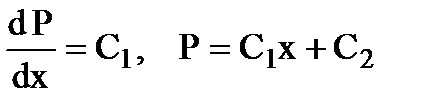
Постоянные интегрирования определим из граничных условий (начальных условий нет, т.к. движение установившееся, т.е. не зависит от t).
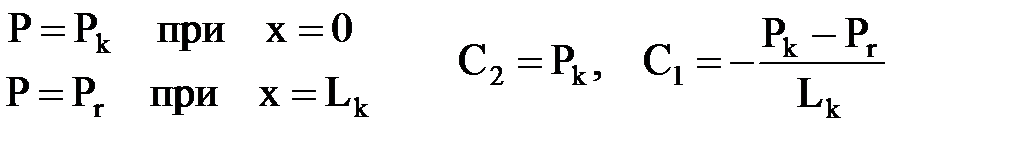
Решением уравнения Лапласа будет функция Р(х) (распределение давления):
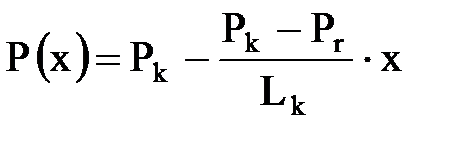
Находим из уравнения движения скорость фильтрации в пласте
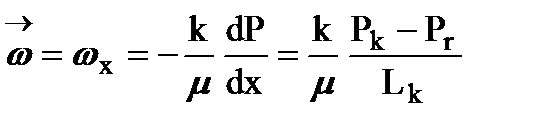
Находим объемный расход жидкости в потоке как произведение скорости фильтрации w на площадь поперечного сечения пласта S = Bh, т.е.
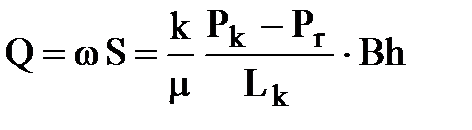
Находим закон движения t = f (x), используя связь между скоростью фильтрации и скоростью движения частиц жидкости
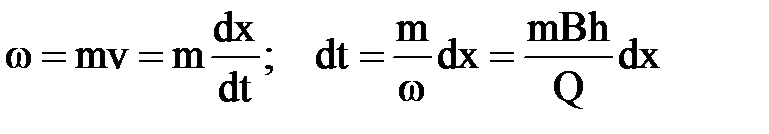
Интегрируя по t от 0 до t и по х от 0 до х, получим
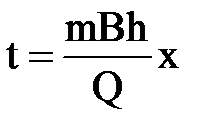
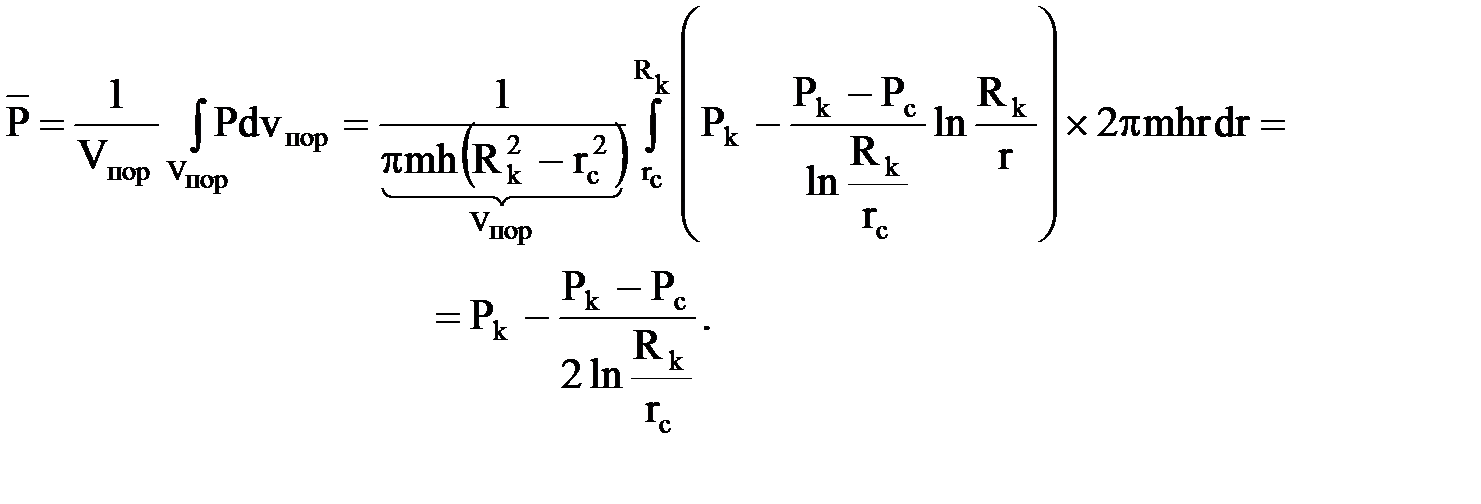
Вычисляем средневзвешенное по объему порового пространства пластовое давление
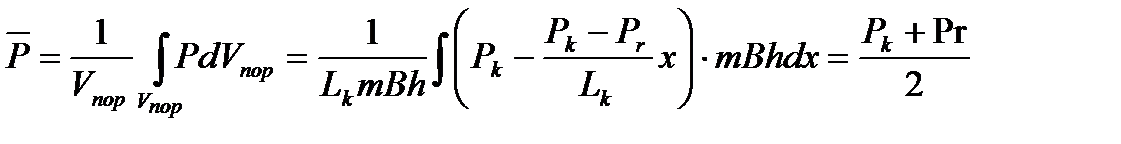
Поведение найденных характеристик плоскопараллельного фильтрационного процесса показано на рис. 10.5 и рис.10.6.
| P |
| Q-const |
| w-const |
| х |
| Рис. 10.5 Изменение характеристик вдоль линий тока. |
| Рис. 10.6 Гидродинамическое поле плоскопараллельного фильтрационного процесса. |
При фильтрации давление равномерно падает от Pk до Pr. Линии равного давления (изобары) на плоскости перпендикулярны кровле и почве пласта и равноотстоят друг от друга. Линии тока жидкости являются параллельными прямыми и перпендикулярны к изобарам. Поведение изобар и линий тока жидкости в пласте определяет гидродинамическое поле данного фильтрационного потока (рис. 10.6).
Лекция № 11
3.5.2 Плоскорадиальный фильтрационный поток.
Лекция № 11
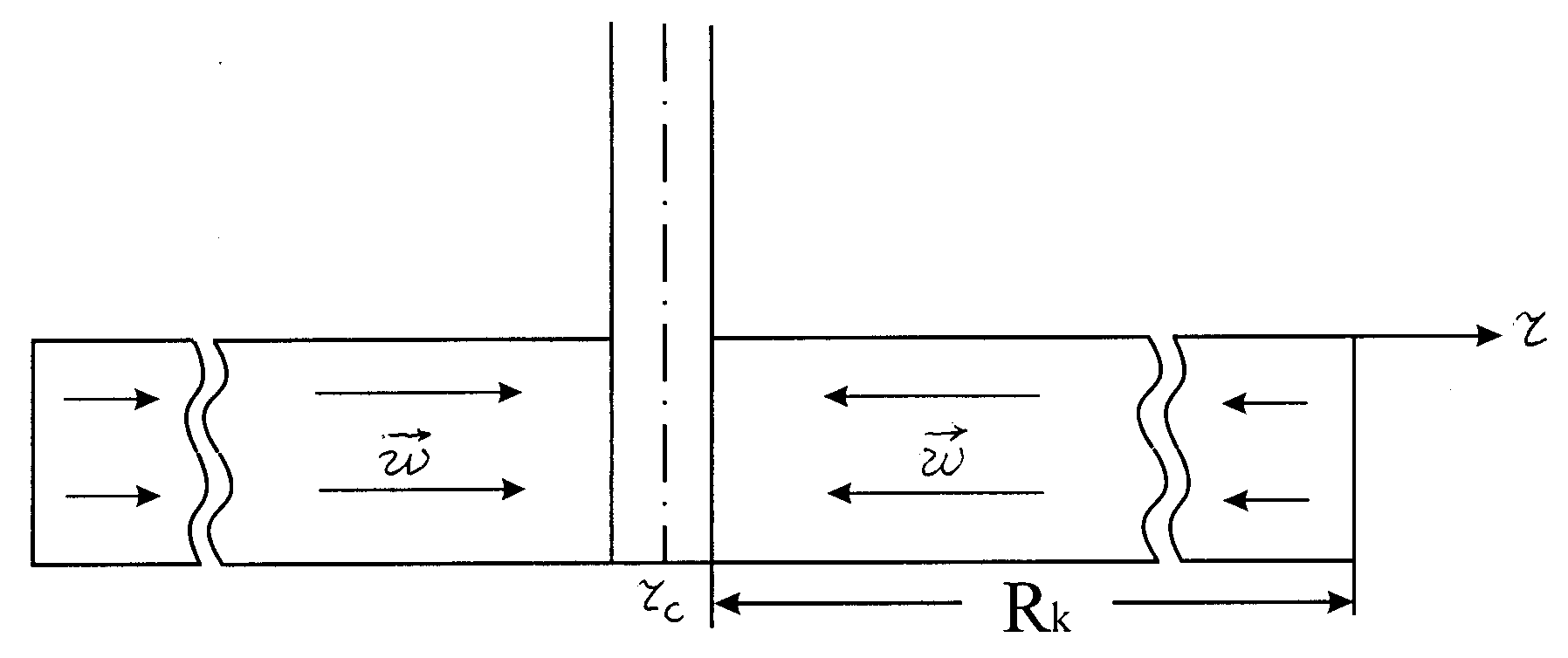
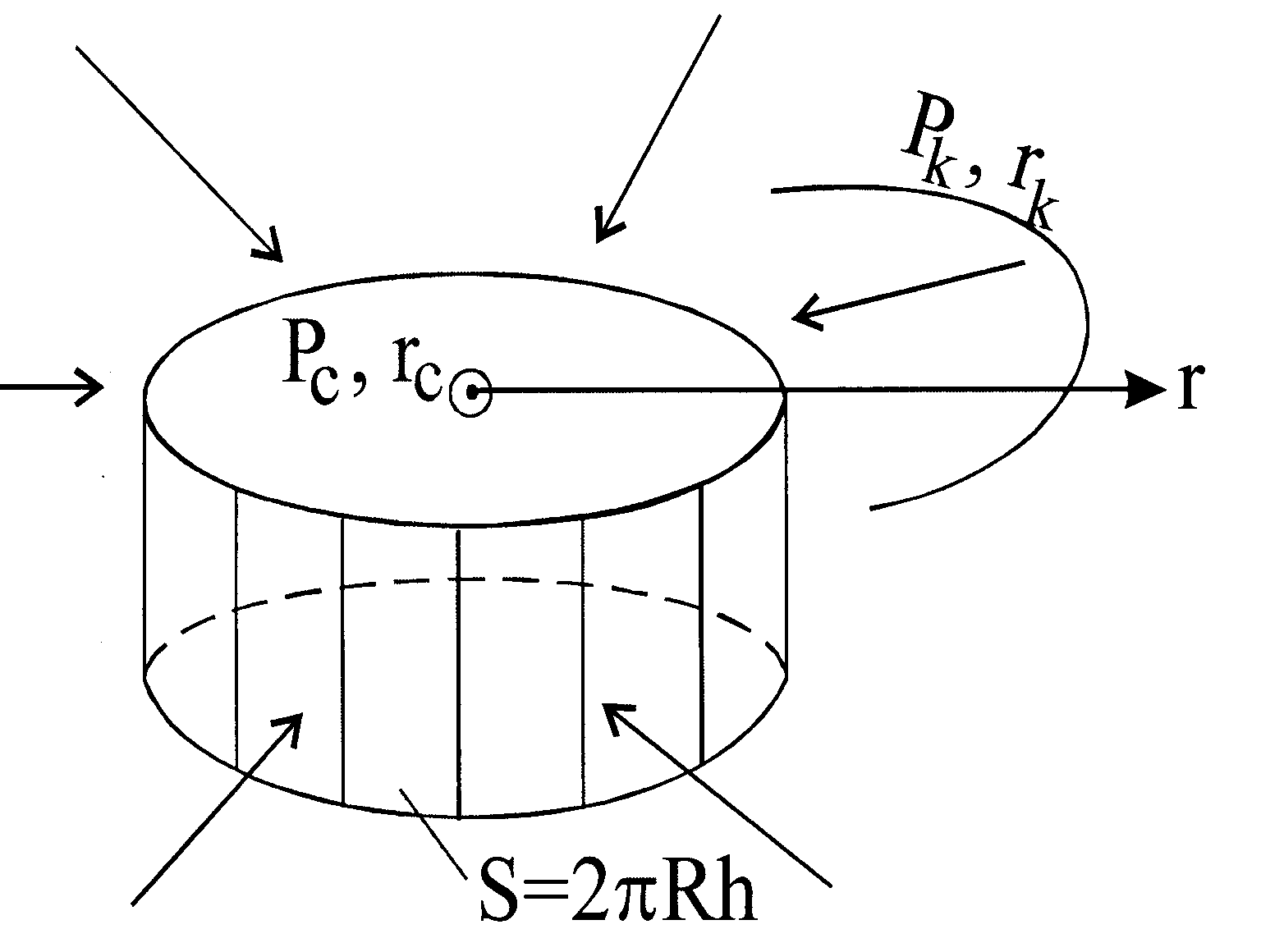
Будем считать, что несжимаемая жидкость притекает к гидродинамической совершенной скважине радиусом rc, расположенной в центре однородного горизонтального кругового пласта, толщиной h. На внешней круговой границе пласта радиусом Rk, служащей контуром питания, поддерживается постоянное давление Pk, на забое скважины давление Рс тоже постоянно. Дифференциальное уравнение Лапласа в случае плоскорадиального фильтрационного потока имеет вид
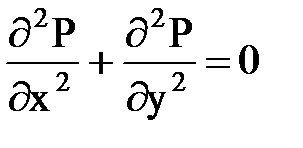
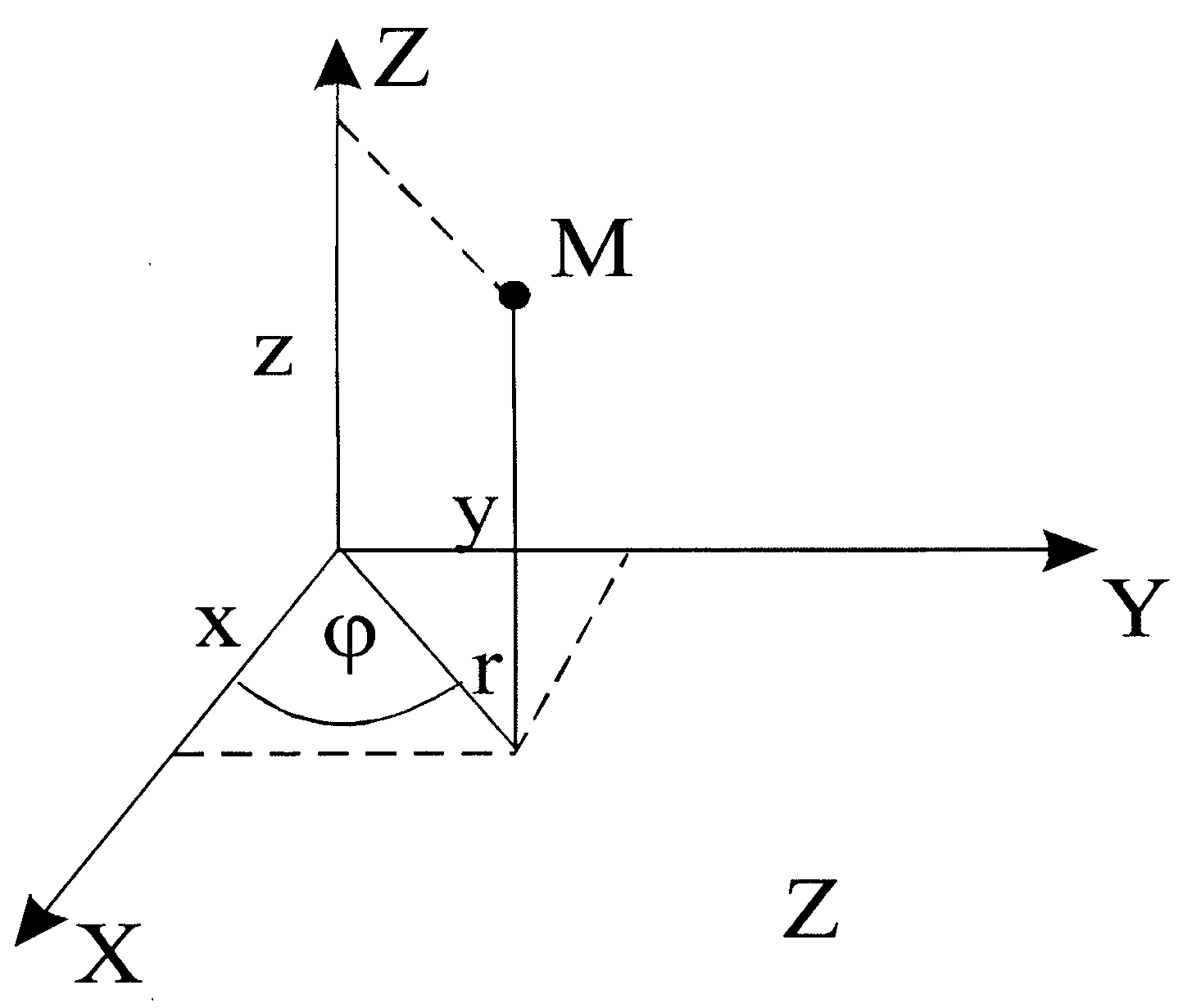
Удобно перейти и решить задачу в цилиндрической системе координат (r,j,z) (рис. 11.1).
| Рис. 11.1 Связь координат декартовой и цилиндрической систем: x = r cos j y = r sin j z = z |
| Рис. 11.2. |
Уравнение Лапласа в криволинейной системе ( цилиндрической) системе координат:
Линии тока жидкости для данной фильтрационной модели совпадают с радиусами окружности (рис. 11.2). Поэтому в уравнении Лапласа останется одно слагаемое, зависимое от координаты r, и после подстановки в него значений коэффициентов Ляме примет вид:
Получаем
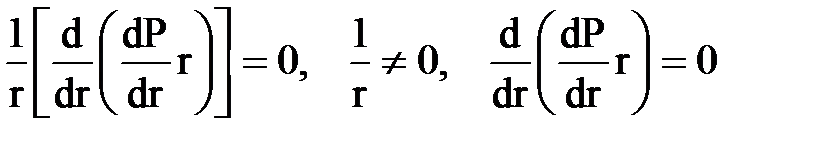
Это и есть дифференциальное уравнение Лапласа в цилиндрических полярных координатах для установившегося плоскорадиального течения несжимаемой жидкости по закону Дарси.
Дважды проинтегрировав дифференциальное уравнение, получаем
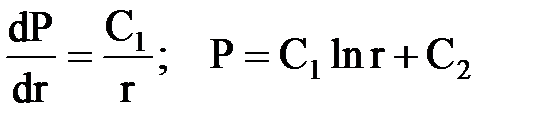
Постоянные интегрирования С1, С2 находим как обычно из граничных условий Р = Рc при r = rc; Р = Рк при r = Rk.
Подставляя граничные условия, получаем систему уравнений для нахождения С1, С2:
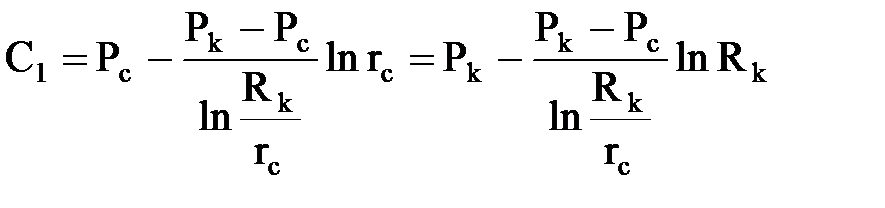
Подставляя найденные значения С1 и С2 в решение, получим зависимость давления от координаты r в плоскорадиальном потоке.
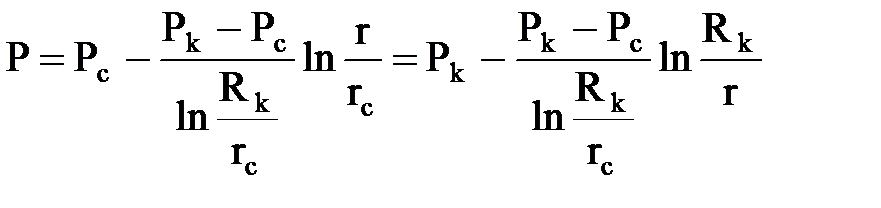
Находим градиент давления
и используем его для нахождения скорости фильтрации
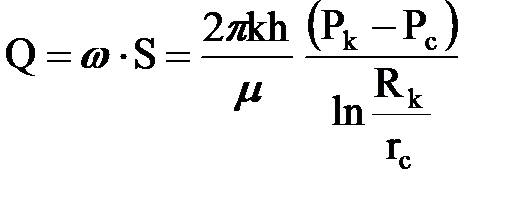
где: S = 2prh – поверхность фильтрации (боковая поверхность цилиндра радиуса r и высотой h) (рис. 11.3).
Формула 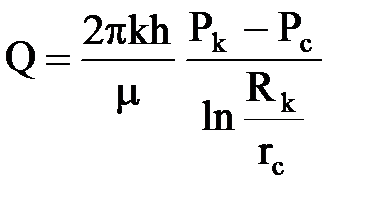
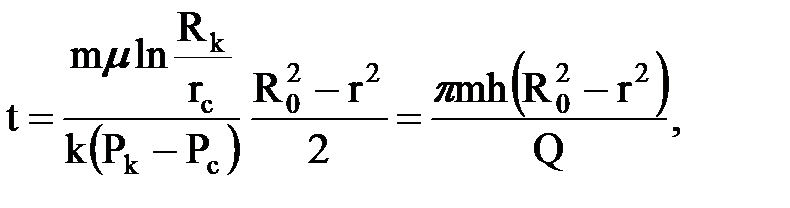 |
Находим закон движения частиц из связи 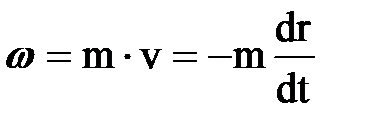 ; ; 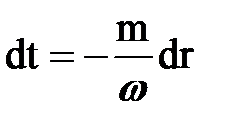 . Подставляя сюда значение w и интегрируя от 0 до t и от R0 до переменного r получим: . Подставляя сюда значение w и интегрируя от 0 до t и от R0 до переменного r получим: |
| Рис. 11.3. |
где: R0 – начальное положение частицы в момент t = 0 и r – текущее положение в момент t.
Если в эту формулу подставить вместо R0 ®Rк , а вместо r ® rc, то получим время Т отбора всей жидкости, находящейся в пласте
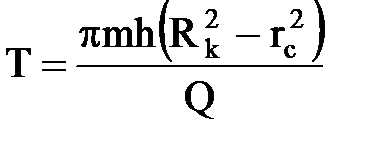
Находим средневзвешенное по объему порового пространства пластовое давление
Прокомментируем некоторые результаты.
Дебит скважины пропорционален депрессии DР (разнице давлений в пласте и на забое работающей скважины) и одинаков через любую цилиндрическую поверхность, соосную со скважиной т.е. не зависит от r.
Отношение объемного дебита скважины к DР называется коэффициентом продуктивности
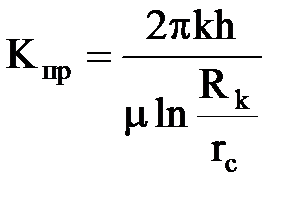
.Через этот коэффициент дебит скважины выражается уравнением
Q=KпрDP , которое называется индикаторной диаграммой. На ней коэффициент продуктивности определяется как тангенс угла наклона прямой к оси DP (tg j = Kпр). На практике индикаторную диаграмму строят по данным испытания скважины, путем получения притоков нефти при различных депрессиях.
| rc |
| r |
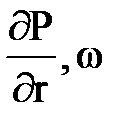 |
| Q |
| DP |
| j |
| Рис. 11.4 |
| Рис. 11.5 График зависимости скорости и градиента давления от расстояния до скважины. |
Градиент давления и скорости фильтрации ведут себя одинаково и резко возрастают при приближении к скважине (рис. 11.5).
Логарифмическая кривая давления, вращение которой вокруг скважины образует поверхность, называется воронкой депрессии. Основная часть депрессии образуется в призабойной зоне, параметры которой сильно влияют на дебит скважины (рис. 11.6).
 |
| Rk Rk |
| Рс |
| rc |
| а) |
| скважина нагнетательная |
| скважина добывающая |
| б) |
 |
| rc |
| Рис. 11.6 Воронка дисперсии (а) и гидродинамическое поле (б) |
Гидродинамическое поле плоскорадиального потока описывается семействами изобар и линий тока. Изобара представляет окружности, поскольку, Р
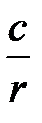
3.5.3 Радиально-сферический фильтрационный поток
Лекция № 12
 |
 |
 |
 |
| r |
| rc |
| Рис. 12.1 Линии тока в радиально-сферическом потоке |
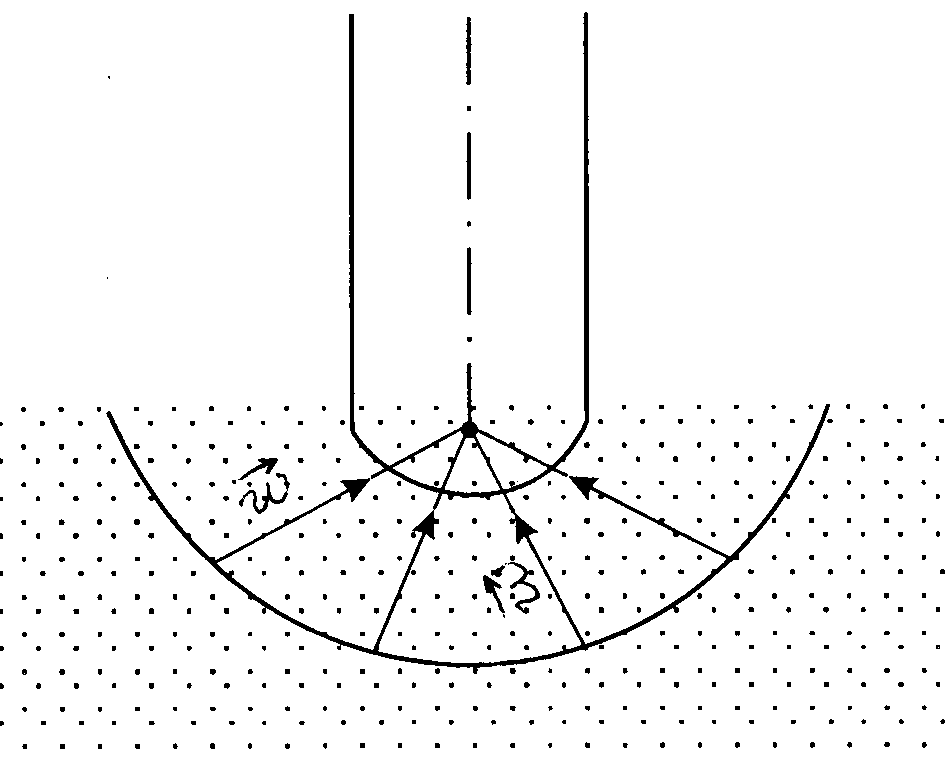
Будем считать, что несжимаемая жидкость притекает к скважине, вскрывающей бесконечный по мощности однородный пласт, через сферический забой радиуса rc. Схема такого потока изображена на рисунке 12.1.
| Дифференциальное уравнение Лапласа удобно решать в сферической системе координат (r, q, j)., т.к. линии тока жидкости совпадают с радиусами полусферы и зависят от одной координаты r. |
 |
где: Нr, Нq, Нj — коэффициенты Ламэ в (r, q, j) : x = r sinq´cosj; y = r sinq ´sinj; z= r cosq (рис. 12.2).
| Рис. 12.2 |
Hr = 1; Hq = r; Hj = r sinq.
Для рассматриваемой модели линии тока жидкости совпадают с радиусами полусферы, поэтому В уравнении Лапласа частные производные по координатам q и j равны 0 и уравнение Лапласа будет иметь вид:
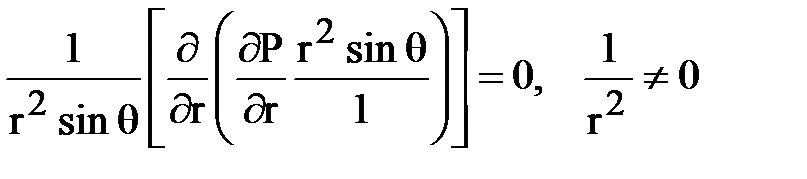
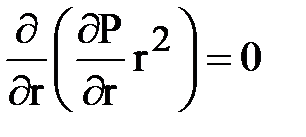
Далее схема решения и нахождения характеристик потока жидкости полностью аналогична плоскорадиальному потоку. Дважды интегрируя, получим
Постоянные С1 и С2 определяем из граничных условий:
Подставив граничные условия, находим С1 и С2 из системы уравнений:
После подстановки значений С1 и С2 в общее решение, получим распределение давления в потоке несжимаемой жидкости как функции от координаты r
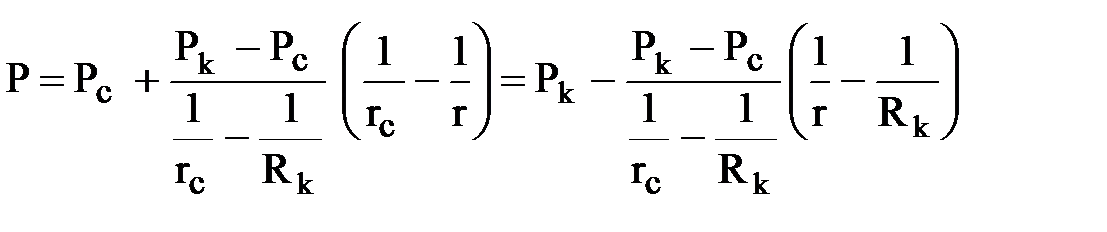
Если сопоставить формулы распределения давления для плоскорадиального и радиально-сферического потоков, то нетрудно заметить, что они имеют одинаковую структуру и переходят друг в друга, если логарифм отношения расстояний заменить разностью обратных значений расстояний:
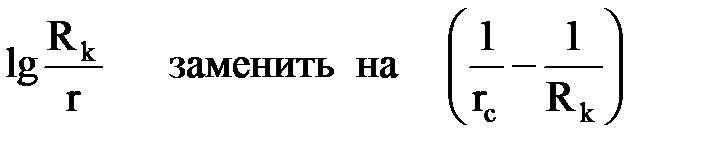
Такое подобие структур формул характерно для выражений всех гидродинамических характеристик. Поэтому все остальные характеристики радиально-сферического потока (объемный расход несжимаемой жидкости, распределение скорости фильтрации, средневзвешенное давление и др.) можно получить из характеристик плоскорадиальной фильтрации аналогичной заменой в соответствующих формулах.
Видео:Гидростатическое давлениеСкачать

Суперпозиция в задачах упругого режима
Метод суперпозиции (наложения фильтрационных потоков) широко применяется и в задачах неустановившихся течений при упругом режиме.
Если в пласте действует группа скважин, то понижение давления в какой-либо точке пласта 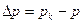

где п — число скважин; Qj — дебит j-той скважины, причем Qj > 0, если скважина эксплуатационная, и Qj 2 (29,4 МПа) до 200 кгс/см 2 (19,6 МПа), если коэффициент сжимаемости нефти 
Пласт считать недеформируемым.
Решение.Считая нефть и воду упругими жидкостями, определим изменение объемов, занимаемых нефтью и водой при падении давления на ∆р =100 кгс/см 2 (9,8 МПа):
объем вытесненной нефти 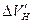
Определить упругий запас нефти в замкнутой области нефтеносности площадью 4500 га, мощностью h=15 м, если средневзвешенное пластовое давление изменилось на 50 кгс/см 2 , пористость пласта m=18%, коэффициент сжимаемости нефти βH = 2,04·10 -9 м 2 /Н, насыщенность пласта связанной водой σв = 20%, коэффициент сжимаемости воды βв = 4,59·10 -10 м 2 /Н, коэффициент сжимаемости породы βс= 1,02·10 -10 м 2 /Н.
Ответ: 
Определить количество нефти, полученное за счет упругого расширения нефти, воды и горной породы, если площадь области нефтеносности SH= 1000га, законтурная вода занимает площадь SВ= 10 000 га, средняя мощность пласта h = 10м, пористость пласта m = 25%, водонасыщенность в зоне нефтеносности σВ=2О%, коэффициенты сжимаемости нефти, воды и породы соответственно равны
Пластовое давление снижается от 180 до 80 кгс/см 2 .
Решение.Коэффициент нефтеотдачи за счет упругого расширения определяется как отношение объема нефти, полученного за счет сжимаемости, к первоначальному объему нефти
Начальный объем нефти
Объем нефти, вытесняемой из зоны нефтеносности при падении давления на ∆р= 100 кгс/см 2 за счет сжимаемости нефти и пористой среды, равен
За счет расширения воды и породы в зоне нефтеносности объем вытесненной нефти составит
Объем нефти, вытесняемой из окружающей зоны водоносности за счет упругости воды и пласта, равен
Определить дебит галереи, расположенной в полосообразном полубесконечном пласте (см. рис. 74) шириной B = 300 м, мощностью h=15м, с коэффициентом проницаемости k = 0,8 Д, в момент t = 2 сут с начала эксплуатации с постоянным забойным давлением рг = 9,8 МПа. Начальное пластовое давление рк= 12,74 МПа, коэффициент сжимаемости жидкости и породыравен соответственно рж = 1,53·10 9 м 2 /Н и рс = 0э612·10 -10 м 2 /Н, коэффициент пористости m = 20%, динамический коэффициент вязкости нефти μ= 1,5 мПа·с.
В пласте имеет место неустановившаяся фильтрация упругой жидкости по закону Дарси.
Найти дебиты по точной формуле и по формуле, полученной по методу последовательной смены стационарных состояний.
Решение. Распределение давления в пласте при неустановившейся параллельно-струйной фильтрации упругой жидкости к прямолинейной галерее при постоянном давлении на забое выражается следующей формулой (точное решение):
Согласно закону Дарси
Найдем 
Коэффициент пьезопроводности א в условиях рассматриваемой задачи равен
Дебит, определенный по точной формуле, будет
По методу последовательной смены стационарных состоянии дебит приближенно определяется по формуле для стационарного режима движения
где l<t)—длина, на которую распространилось бы понижение давления к моменту t, если бы давление в зоне депрессии менялось по прямой линии; l(t) определяется из условия материального баланса при pГ = const и равна
Погрешность при определении дебита по приближенной формуле составит
Представить графически изменение во времени давления на забое галереи, проведенной в полосообразном полубесконечном пласте (см. рис. 74), если в момент t= 0 ее начали эксплуатировать с постоянным дебитом Q = 500 м 3 /сут. Ширина галереи В = 400 м, мощность пласта h= 18 м, коэффициент проницаемости k = 0,5 Д, коэффициенты сжимаемости жидкости βж =2,04·10 -9 
В пласте имеет место неустановившаяся фильтрация упругой жидкости по закону Дарси.
Сравнить значение депрессии в момент t =10 сут, определенное по точной формуле, с депрессией, найденной по методу последовательной смены стационарных состояний.
Решение. Врассматриваемом случае дифференциальное уравнение фильтрации упругой жидкости в деформируемой пористой среде имеет вид

а начальное и граничные условия запишутся следующим образом:


Умножая (XII.22) на 

или, изменяя порядок дифференцирования,

Уравнение теплопроводности (XII.25) совпадает с уравнением (XII.22), и начальным и граничным условиями являются:
Решением уравнения (XII.25) при условиях (XII.26) и (XII.27) является интеграл вероятности

Для того, чтобы найти закон изменения давления, необходимо проинтегрировать по х уравнение
при фиксированном t:

Возьмем по частям интеграл

Подставив (XII.30) в (XII.29), получим
Устремляя 
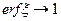
найдем депрессию в любой момент времении
давление па забое галереи
Подсчитаем коэффициент пьезопроводностии
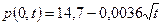
Задаваясь различными 

График зависимости 

Определим депрессию по методу последовательной смены стационарных состояний через 
Соответствующая депрессия, определенная по точной формуле (см. табл. 15), равна
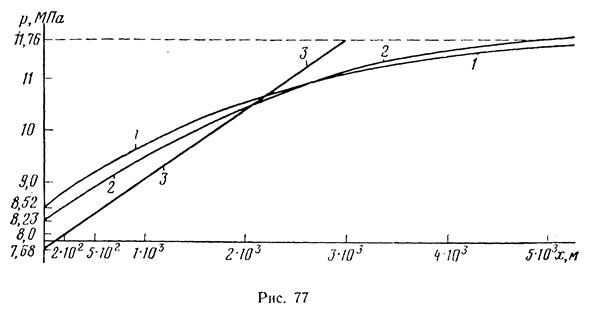
Найти распределение давления в полосообразном полубесконечном пласте в момент t ==15 сут с начала отбора, если в пласте имеет место приток упругой жидкости к дренажной галерее при условии постоянного отбора Q = 100 м 3 /сут; длина галереи В = 250 м; мощность пласта h == 10 м, коэффициент проницаемости k = 400 мД, коэффициент сжимаемости пористой среды рс = 0,306 • 10 -10 м 2 /Н, коэффициент сжимаемости жидкости βж = 4,59·10 -10 м 2 /Н, динамический коэффициент вязкости μ = l,2 мПа·с, коэффициент пористости m=l5%, начальное пластовое давление рк= 11,76 МПа (120 кгс/см 2 ).
Задачу решить по точной формуле, по методу последовательной смены стационарных состояний и по методу А. М. Пирвердяна
Решение.В задаче 111выведена точная формула для разности давлений

Из этой формулы давление на забое галереи равно

Подставив (XII.32) в (XII.31), получим

Вычислим постоянные множители:
при этом 
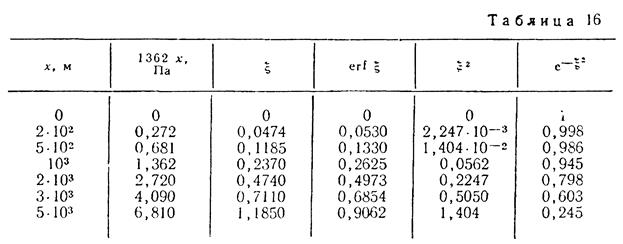
По приближенному методу А. М. Пирвердяна при постоянном отборе

При заданном t=15 сут

Результаты вычислений по (XII.35) приведены в табл. 17 и ,на рис. 77 (кривая 2).
По методу последовательной смены стационарных состояний давление распределяется линейно

давление на забое галереи

Прямая 3, соответствующая уравнению (XII.37), изображена на рис. 77.
Как видно из полученных результатов, распределение давления по методу Пирвердяна ближе к истинному, чем распределение давления по методу последовательной смены стационарных состояний.
Из скважины, расположенной в бесконечном пласте, начали отбор нефти, поддерживая постоянное давление на забое рс = 8,82 МПа. Начальное пластовое давление pk= 11,76 МПа. Используя метод последовательной смены стационарных состояний, определить дебит скважины через 1 ч, 1 сут и 1мес после начала эксплуатации, если коэффициент проницаемости пласта k = 250 мД, мощность пласта h = 12 м, коэффициент пьезопровод-пости пласта א = 1,5 м 2 /с, коэффициент вязкости нефти μ=l,3 сП. Скважина гидродинамически совершенная, радиус ее rс = 0,1 м.
Указание.По методу последовательной смены стационарных состояний дебит скважины определяется по формуле Дюпюи, в которой под Rk понимается приведенный радиус влияния скважины, который увеличивается с течением времени по закону 
Ответ:Qчас = 515м 3 /сут; Qcyт = 424 м 3 /сут; Qмес = 356 м 3 /сут.
Определить коэффициент гидропроводности пласта 

Номер ……………………..1 2 3 4 5
t . 15 мин 1 ч 12 ч 1 сут 5 сут

Решение.Изменение давления на забое скважины определяется по формуле
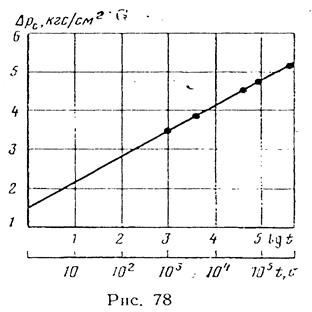


Как видно из рис. 78, зависимость 

Это дает возможность определить свободный член по отрезку, отсекаемому прямой на оси ординат, и коэффициент при 

Из графика следует, что b = 1,5 кгс/см 2 ,
Из первой формулы следует, что
откуда коэффициент гидропроводности пласта
Гидродинамически совершенная скважина, расположенная в центре кругового пласта радиуса Rk=10 км с горизонтальными и непроницаемыми кровлей и подошвой, до момента остановки работала в течение такого продолжительного периода, что распределение давления в пласте можно принять за установившееся. Дебит скважины до остановки Q = 120 м 3 /сут, динамический коэффициент вязкости μ = 2 сП, коэффициент проницаемости пласта k = 600 мД, мощность пласта h = 10 м, радиус скважины rс = 0,1 м, коэффициент пьезопроводности пласта א = 2,5 м 2 /с Найти по методу суперпозиции нарастание давления на забое скважины, принимая pk = 14,7 МПа (150 кгс/см 2 ).
Решение.Установившуюся депрессию 
По методу суперпозиции считаем, что с момента остановки скважины в той же точке пласта начала работать одновременно с эксплуатационной скважиной нагнетательная скважина, имеющая тот же дебит. При этом результирующий дебит равен нулю, а разность давлений
где 
Определить коэффициент гидропроводности пласта 
Изменение давления на забое скважины во времени представлено ниже. Время t = 0 соответствует моменту изменения-дебита скважины.
Номер ……………….1 2 3 4 5 6
t ……………………. 5 мин 15 мин 3 ч 1 сут 3 сут 10 сут
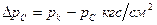

Решение. По принципу суперпозиции понижение давления на забое скважины найдем по формуле
где первое слагаемое определяет депрессию, вызванную длительной эксплуатацией скважины с дебитом Q, а второе слагаемое—повышение давления за счет действия в той же точке пласта нагнетательной скважины с дебитом (Q— Q1).
Представляя приближенно интегральную показательную функцию через логарифм, получим
Выделяя слагаемое, содержащее 
Из последней формулы видно, что зависимость ∆рс от lg t прямолинейная с угловым коэффициентом
По приведенным выше данным построим график в координатах ∆рс — lgt и определим значение i (рис. 79).
По полученному значению i найдем коэффициент гидропроводноети
Гидродинамическая совершенная скважина радиусом rC = 10 см начала работать в бесконечном пласте с постоянным дебитом Q=80 м 3 /сут. Мощность пласта h = 7,5 м, коэффициент проницаемости k = 400 мД, коэффициент пьезопроводности א = 2 м 2 /с, динамический коэффициент вязкости жидкости μ = 1,5·10 -3 Па·с. По истечении T=10 сут скважина была мгновенно остановлена. Определить: 1) распределение давления в пласте в моменты t1=l сут и 
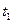

Решение.Используя метод суперпозиции, найдем результирующее понижение давления в любой точке пласта

считая, что в некоторый момент времени пущена в эксплуатацию скважина с постоянным дебитом, а через промежуток времени Т в этой же точке пласта начала работать нагнетательная скважина с тем же дебитом. Время Т соответствует моменту мгновенной остановки эксплуатационной скважины, начиная с этого момента отбор жидкости из пласта равен нулю.
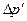



Учитывая выражения (XII.39) и. (XII.40), получим

Известно, что при малых значениях аргумента 

Погрешность не превышает 1%, если
или 
Поэтому (XII.41) можно записать в виде

при выполнении условия (XII.42).
Как следует из (XII.43), в некоторой области пласта, определяемой условием (XII.42), для одного и того же момента времени давление будет одинаково.
При t1 = 1 сут эта зона ограничена радиусом
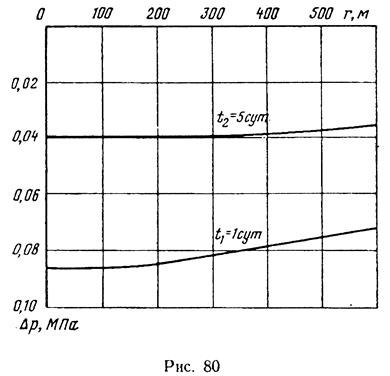
Понижения давления в этих зонах соответственно равны
📽️ Видео
Епихин АВ Буровой Ликбез. Пластовое давление. 2020Скачать

Закон БернуллиСкачать

Гидродинамические исследования скважинСкачать

Воп.–Отв. №17."Как рассчитать давление на контуре питания на любом расстоянии от забоя скважины"Скачать

Давления поглощения и гидроразрыва, ч.8 #епихин #буровойликбез #бурение #давлениеСкачать

Разработка нефтяных месторождений подразумевает использование ППД (заводнение пласта) для добычиСкачать

20. С.В. Головин. Моделирование гидроразрыва пласта: теория и экспериментСкачать

Вызов притока и освоение скважин. Методы вызова притока. НефтянкаСкачать

Гидродинамическое моделирование (Part 1. PRE-PROCESSING)Скачать

Тема 10. Методы поддержания пластового давления.Скачать

Профессия "Оператор по поддержанию пластового давления"Скачать

Вопрос–Ответ №7. Геология. Проницаемость пласта и её виды, что это?Скачать

Основные давления при матричной обработки продуктивного пласта с целью интенсификации добычиСкачать

Давление поглощения и гидроразрыва ч.3 #епихин #буровойликбез #бурение #давлениеСкачать

Межфазное натяжение, смачиваемость, капиллярное давлениеСкачать

Прочность пласта. Управление скважиной при бурении наземным ПВОСкачать

Замер пластового давления в пьезометрических скважинах Урьевского месторожденияСкачать

Материалы для ГРП. Гидроразрыв пласта. Добыча нефти и газа. Технологии нефтедобычи.Скачать