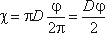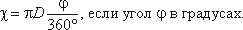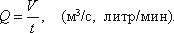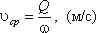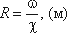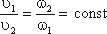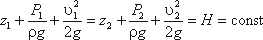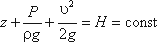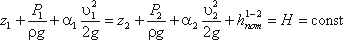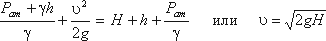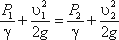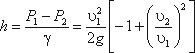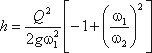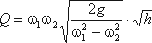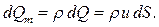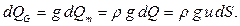Уравнение расхода и средняя скорость потока (3 видео)

Уравнение расхода и средняя скорость потока

Гидродинамика — раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие с неподвижными и подвижными поверхностями.

Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

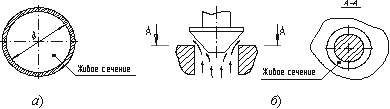
Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения. Например, живое сечение трубы — круг (рис.3.1, б); живое сечение клапана — кольцо с изменяющимся внутренним диаметром (рис.3.1, б).

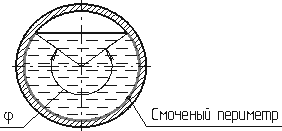
Смоченный периметр χ («хи») — часть периметра живого сечения, ограниченное твердыми стенками (рис.3.2, выделен утолщенной линией).

Для круглой трубы

если угол в радианах, или

Расход потока Q — объем жидкости V, протекающей за единицу времени t через живое сечение ω.

Средняя скорость потока υ — скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Гидравлический радиус потока R — отношение живого сечения к смоченному периметру

Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Трубка тока — трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой.

Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением). Безнапорное — течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые каналы, лотки и т.п.). В данном курсе будет рассматриваться только напорное течение.

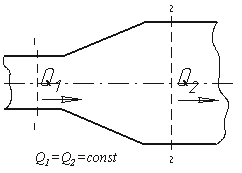
Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q₁=Q₂= const, откуда

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.

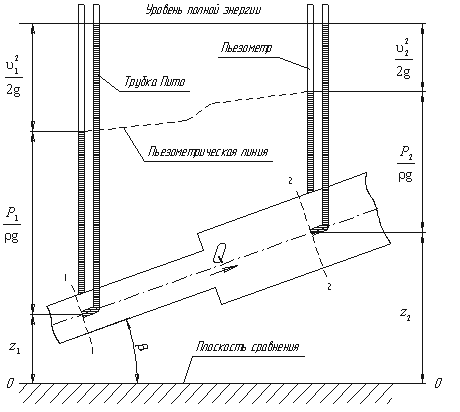
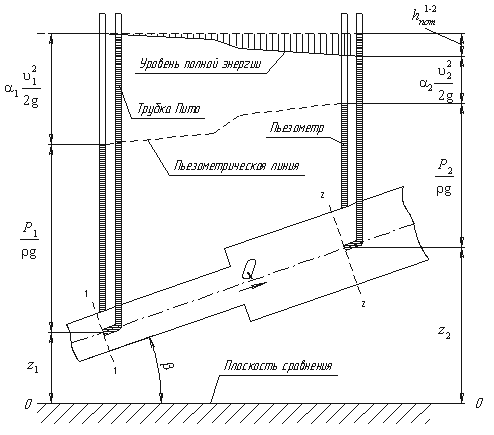
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).

Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.

Для измерения давления жидкости применяют пьезометры — тонкостенные стеклянные трубки, в которых жидкость поднимается на высоту 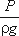. В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.

Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).

Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.

Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.

Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:

Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.

С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:

z1 и z2 — удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;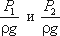
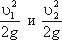
— удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
— удельные кинетические энергии в тех же сечениях.

Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.

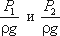
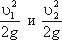
Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рис.3.5, можно заметить, что z1 и z2 — геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения; — пьезометрические высоты; — скоростные высоты в указанных сечениях.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).

Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α₁ и α₂, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).

Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

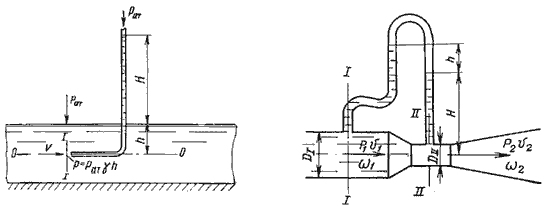
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

где Н — столб жидкости в трубке Пито.

Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:

Выражение, стоящее перед 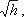, является постоянной величиной, носящей название постоянной водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.

Содержание

Расход, средняя скорость. Уравнение расхода (неразрывности)
Уравнение неразрывности и уравнение Бернулли.
Уравнение неразрывности потока жидкости
Уравнение неразрывности струи жидкости. Уравнение Бернулли.
Видео по теме уравнение неразрывности
🎦 Видео

Видео:Урок 16 (осн) Средняя скорость. Вычисление пути и времени движенияСкачать

Расход, средняя скорость. Уравнение расхода (неразрывности)

Расход – количество жидкости, проходящее через живое сечение потока (элементарной струйки) в единицу времени.

Данное количество жидкости можно измерять в единицах объема, массы и веса. Поэтому различают объемный Q, массовый Q_m и весовой Q_G расходы.

Для элементарной струйки, имеющей бесконечно малые площади живых сечений dS можно считать скорость u одинаковой во всех точек каждого сечения (см. рис. 4.2). Тогда для элементарной струйки объемный dQ, массовый dQ_m и весовой расходы dQ_G с учетом уравнений (2.1) и (2.2) будут равны:

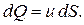
Объемный расход потока жидкости можно определить как сумму расходов элементарных струек:

(4.3)

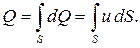
В инженерных расчетах воспользоваться уравнением (4.3) достаточно сложно, поэтому введено понятие средней скорости.

Средняя скорость потока – фиктивная скорость, с которой якобы движутся все частицы жидкости в данном живом сечении потока, но расход при этом равен расходу, вычисленному по действительным скоростям элементарных струек. Тогда

(4.4)

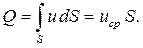
Исходя из закона сохранения вещества, сплошности (неразрывности) течения и непроницаемости трубки тока можно утверждать, что при установившемся течении несжимаемой жидкости во всех живых сечениях элементарной струйки расход постоянен (см. рис. 4.2):

(4.5)

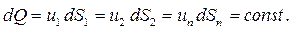
Уравнение (4.5) называется уравнением объемного расхода (сплошности, неразрывности) для элементарной струйки. Для потока несжимаемой жидкости с учетом (4.4) получим:

(4.6)

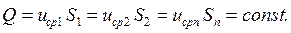
Уравнение (4.6) является частным случаем закона сохранения вещества при условии сплошности (неразрывности) течения.

При установившемся движении сжимаемой жидкости (газа) плотность в различных сечениях потока может быть различной, но масса газа, проходящая через живое сечение, будет постоянной. Тогда уравнение расхода для сжимаемой жидкости (газа) будет иметь вид:

(4.7)

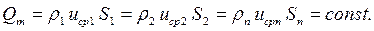
Следует отметить, что уравнение (4.7) справедливо и для несжимаемой жидкости. При этом ρ₁= ρ₂= ρ_n=const.

Видео:Закон БернуллиСкачать

Уравнение неразрывности и уравнение Бернулли.

Уравнение неразрывности потока и уравнения Бернулли являются основными уравнениями гидродинамики. При изучении потоков жидкости вводится ряд понятий, характеризующий потоки с гидравлической и геометрической точек зрения.

Такими понятиями являются: площадь живого сечения потока(или живое сечение потока), расход и средняя скорость.

Площадью живого сечения потока, называют площадь сечения потока, приведенную нормально к направлению линии тока, т.е. перпендикулярно движению струйки жидкости. Живое сечение может быть ограничено твердыми стенками полностью или частично. Если стенки ограничивают поток полностью, то движение жидкости называют напорным; Если же ограничение частичное, то движение называется безнапорным.

Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше него. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному.

Содержание статьи

Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.

Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным. Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью. Эту воображаемую фиктивную скорость называют средней скоростью потока υ_ср .

Таким образом уравнение расхода для потока будет

υ_ср – средняя скорость потока

F – площадь сечения потока.

Видео:Что такое расход жидкости, способы измерения объемного и массового расходаСкачать

Уравнение неразрывности потока жидкости

Теперь вооружившись основными понятиями перейдем к определению уравнения неразрывности потока.

Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный

а через сечение 2-2 из него же вытекает объем, равный

Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.

Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.

Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки

Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что

т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.

Уравнение неразрывности струи жидкости. Уравнение Бернулли.

Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.

При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.

Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.

Если всё это записать в виде формулы, то

где W – приращение кинетической энергии = m * υ 2 / 2

ΣA – сумма работ действующих сил = P *ΔS

В этих выражениях
m – масса
υ – скорость материальной точки
P – равнодействующая всех сил, приложенных к точке,
ΔS – проекция перемещения точки на направление силы.

Теперь рассмотрим обе части этого выражения по порядку.

Приращение кинетической энергии ΔW

В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.

Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.

Вспоминая, что по условию неразрывности расход во всех сечениях элементарной струйки одинаков, а следовательно будет равен

масса в этом случае получается равной

Подставляя все это в выражение для кинетической энергии получаем цепочку

ΔW = m * υ 2 ₂ / 2 — m * υ 2 ₁ / 2 = ρ * q * ΔТ * υ 2 ₂ / 2 — ρ * q * ΔТ * υ 2 ₁ / 2

Работа сил действующих на систему ΣA

Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести A_Т равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.

Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z1 –Z2.

Где Z1 и Z2 – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.

Силы давления А_Д , действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.

Суммарно работа сил давления будет

Подставляя в начальное уравнение

Полученные выражения для ΔW и ΣA получаем

Разделим обе части этого уравнения на m = ρ*q*ΔТ и перегруппируем слагаемые

Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:

Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки. Различают такие энергии как:
Удельная энергия положения = qz
Удельная энергия давления = p/ ρ
Кинетическая удельная энергия = υ 2 / 2

В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Видео по теме уравнение неразрывности

Полученные в результате многочисленных экспериментов данные из уравнения Бернулли и уравнения неразрывности потока жидкости нашли широкое применение в повседневной жизни.

Уравнение Бернулли широко используется для нахождения скорости истечения жидкости через отверстия.

Уравнение неразрывности обладает широкой универсальностью и справедливо для любой сплошной среды. Принцип уравнения неразрывности используется для формирования сильной и дальнобойной струи воды при тушении пожаров.