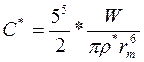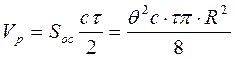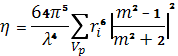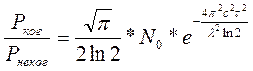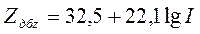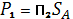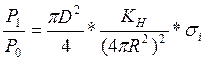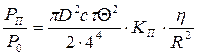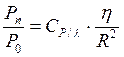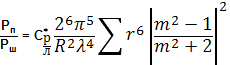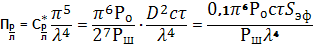Уравнение радиолокации в ближней зоне

Ближняя и дальняя зоны

Ближняя зона и дальняя зона заданного источника электромагнитного излучения — это термины, обычно используемые при антенных измерениях, и при описании областей пространства вокруг такого источника, в которых различные составляющие поля играют большую или меньшую роль. Граница между этими двумя зонами зависит от геометрических размеров источника излучения и основной длины волны λ λ . В ближней зоне антенны угловое распределение поля зависит от расстояния до антенны. Разные составляющие поля, излучаемые разными геометрическими частями поверхности антенны, имеют разное время распространения до точки наблюдения и поэтому они будут интерферировать между собой (не обязательно синфазно), формируя волновой фронт.

Точечный изотропный источник не может иметь ближней зоны. Ближняя зона возникает если размер источника как минимум соизмерим с длиной волны λ . Ближняя и дальняя зоны представляют собой математические абстракции, введенные для упрощения получения аппроксимации уравнений Максвелла. В ближней зоне существует также область, в которой антенна улавливает часть только что излученной ею энергии.

Рисунок 1. Ближняя зона антенной решетки

Рисунок 1. Ближняя зона антенной решетки

Рисунок 1. Ближняя зона антенной решетки

На Рисунке 1 изображена решетка из четырех синфазно запитанных элементов. Каждый из элементов излучает электромагнитное поле. Эти частные поля складываются в общее поле. Хотя рисунок большой, все показанные на нем расстояния находятся в ближней зоне. Чтобы изобразить дальнюю зону размер рисунка следовало бы увеличить как минимум в четыре раза, для того, чтобы показать как поля излучения отдельных элементов решетки, складываясь, формируют когерентный волновой фронт. В дальней зоне форма диаграммы направленности антенны не зависит от от расстояния до источника излучения.

Для маленьких антенн (размер излучателя меньше длины волны) ближняя зона представляет собой область радиуса r , а дальняя зона — область радиуса r >> λ .

Для больших антенн (антенных решеток или антенн, использующих большие отражатели, таких как параболические зеркальные антенны) границу между двумя зонами можно приближенно рассчитать по формуле:

Дальнюю зону иногда называют зоной Фраунгофера , а ближнюю зону — зоной Френеля .

Часть зоны Френеля представляет собой промежуточную область, в которой происходит как излучение так и поглощение (сбор) энергии. Граница этой области находится вблизи расстояния D²/(2·λ) , а саму область иногда называют зоной Рэлея .

В качестве примера проанализируем антенну THALES-MSSR, используемую в радиолокаторе управления воздушным движением ASP-909, состоящую из 35 вертикальных элементов и имеющую апертуру 8,5 метров. В примере используем значение частоты излучения вторичного канала радиолокатора, которое равно 1030 МГц. Данному значению частоты соответствует значение длины волны, равное 0,291 м. На основе этих данных рассчитаем расстояние от антенны, на котором будет сформирован луч.

• Дальняя зона начинается с расстояния 497 м..
• Зона Рэлея — до расстояния 124 м

Измерительные приборы для снятия диаграммы направленности антенны должны располагаться не ближе 497 метров от антенны. Рекомендуется выбирать позицию для измерений даже на еще большей дальности.

Издатель: Кристиан Вольф, Автор: Андрій Музиченко
Текст доступен на условиях лицензий: GNU Free Documentation License
а также Creative Commons Attribution-Share Alike 3.0 Unported License,
могут применяться дополнительные условия.
(Онлайн с ноября 1998 года)

Видео:Лекция по радиолокации. Инженер Степанов Ф.М.Скачать

Уравнение радиолокации в ближней зоне

ЦИФРОВОЕ МОДЕЛИРОВАНИЕ ВХОДНЫХ СИГНАЛОВ СИСТЕМ БЛИЖНЕЙ РАДИОЛОКАЦИИ ОТ СЛОЖНЫХ РАДИОЛОКАЦИОННЫХ СЦЕН

А.Б.Борзов, А.В.Соколов, В.Б.Сучков

Получено 05 апреля 2004 г.

Рассмотрена математическая модель входных сигналов систем ближней радиолокации (СБРЛ) от радиолокационных сцен, внешняя поверхность которых задана в виде полигональной модели. Показано, что использование полигональной модели сцены позволяет представить сферическую волну, облучающую радиолокационную сцену, суперпозицией локально плоских волн. Получена математическая модель спектра доплеровских частот входного сигнала СБРЛ, позволяющая учитывать расширение спектра отраженного сигнала за счет эффекта взаимного перемещения СБРЛ и объекта. В результате цифрового моделирования на ЭВМ получены характеристики входных сигналов СБРЛ и характеристики рассеяния сложных объектов в ближней зоне локации.

Digital simulation of input signals of systems of a near radar-location from complex radar-tracking scenes

A.B.Borzov, A.V.Sokolov, V.B.Suchkov

The mathematical model of input signals of systems of near radar-location from radar-tracking scenes which external surface is set as polygonal model is considered. It is shown, that use of polygonal model of a scene allows to present the spherical wave irradiating a radar-tracking scene by superposition of locally plane waves. The mathematical model of a spectrum of Doppler frequencies of an input signal of the system is received, allowing to take into account expansion of a spectrum of the reflected signal due to effect of mutual moving system and object. As a result of digital simulation on the computer characteristics of input signals of the systems and characteristics of scattering of complex objects in a near-field zone of a location are received.

Видео:Распространение радиоволн. Радиолокация. 11 класс.Скачать

1. Введение

Одной из тенденций современной радиолокации является развитие теории и техники систем ближней радиолокации (СБРЛ), к которым относятся бортовые системы измерения дальности, радиолокационные датчики цели и т.д. Специфика функционирования СБРЛ состоит в том, что обнаружение радиолокационных объектов, определение их координат и параметров движения осуществляется на дальностях, сопоставимых с геометрическими размерами самих объектов [1]. При этом СБРЛ работают на конечных участках траекторий столь незначительной протяженности, что изменение траектории полета объекта здесь уже не происходит. Характерной функциональной особенностью СБРЛ является также выдача исполнительных команд в определенной области пространства вблизи объекта.

В качестве физических особенностей функционирования СБРЛ, определяющих характер электромагнитного взаимодействия антенны СБРЛ с объектом, можно выделить такие явления как существенно сферический фронт облучающей волны вблизи объекта, эффект трансформации поляризационного базиса излученной электромагнитной волны и возникновение спектра доплеровских частот отраженного от объекта сигнала. В условиях малой дальности, когда объект уже нельзя считать сосредоточенным, а облучающую волну плоской, неизбежно возникают серьезные специфические проблемы, характерные для ближней зоны локации. Поэтому использование принципов, методов и представлений, принятых для дальней зоны в условиях ближней зоны не представляется возможным.

В соответствии с [2] предельное расстояние, на котором фронт падающей волны можно считать плоским определяется в соответствии с критерием дальней зоны:

где l — длина волны падающего излучения, — предельное расстояние между СБРЛ и объектом.

В качестве энергетической характеристики рассеяния объекта в дальней зоне локации используется эффективная площадь рассеяния (ЭПР) [2], которая определяется для сосредоточенного объекта при облучении его плоской электромагнитной волной:

где R – расстояние от фазового центра антенны до объекта, — величина напряженности поля, падающего на объект, — вектор поляризации приемной антенны в дальней зоне локации, — вектор напряженности электрического поля рассеяния объекта в точке приема.

Функционирование СБРЛ осуществляется в так называемой ближней зоне локации [2], когда СБРЛ находится на таком расстоянии до объекта, что критерий дальней зоны (1) не выполняется, а падающая на объект электромагнитная волна имеет в месте его расположения существенно сферический фронт. При этом определение ближней зоны локации никак не связано с ближней зоной излучения антенны, и зависит только от расстояния между СБРЛ и объектом. Кроме того, возникает вопрос о том, что считать ЭПР объекта в ближней зоне локации, когда соотношение (2) не выполнимо. Таким образом, для решения указанных проблем требуется создание единого методического подхода, позволяющего наиболее адекватно описывать процесс электромагнитного взаимодействия СБРЛ и объекта как в ближней, так и в дальней зоне локации.

Одним из приоритетных направлений совершенствования принципов и методов радиолокационного обнаружения объектов на фоне подстилающих поверхностей и при наличии помех в СБРЛ является разработка новых более совершенных методов математического и цифрового моделирования рассеяния электромагнитных волн в ближней зоне локации.

Современный уровень развития вычислительных средств и средств автоматизированного проектирования позволяет использовать для решения задач математического моделирования отражательных характеристик объектов геометрические модели, основанные как на аналитических принципах описания поверхности, так и представляющие внешнюю поверхность объекта в виде совокупности плоских элементов (фацетов). В результате многолетних исследований в МГТУ им. Н.Э.Баумана разработана математическая модель радиолокационных характеристик цели, геометрия которой была описана в виде кусочно-аналитической модели [3]. Опыт использования этой модели показал, что в оптическом диапазоне эта модель позволяет получить достаточно хорошие результаты. Однако в диапазоне ультракоротких радиоволн, где требования к точности аппроксимации внешнего облика объекта становятся определяющими, данная модель в ряде случаев оказывается непригодной. К основным достоинствам кусочно-аналитической модели следует отнести ограниченное количество базовых пространственных элементов, аналитический характер поверхности, реализацию библиотеки «геометрических» функций, специализированное программное обеспечение по генерации 3-D модели сложного объекта. При этом основными недостатками кусочно-аналитической модели являются ограниченные возможности в достижении высокой точности аппроксимации внешнего облика объекта. Кроме того, данная модель была изначально предназначена для решения задач рассеяния линейно поляризованных электромагнитных волн от целей, находящихся в дальней зоне локации. Поэтому использование кусочно-аналитической модели в задачах ближней радиолокации объектов сложной формы нецелесообразно, поскольку затраты на модернизацию этой модели к современным требованиям окажутся чрезмерными.

В настоящее время развитие методов математического моделирования электромагнитных полей рассеяния сложных объектов и радиолокационных сцен в дальней и ближней зонах локации, связано с использованием так называемых полигональных моделей, формируемых в среде современных систем автоматизированного проектирования (САПР) [4]. Именно использование САПР позволяет синтезировать геометрическую модель объекта локации практически любой формы и конфигурации на основе чертежей общего вида или эскизных моделей. К числу наиболее мощных САПР следует отнести такие системы как Pro/Eng i neer, UniGraphics, MatraDV и Catia. Поскольку эти системы используются для формирования отдельных конструктивных элементов и всего сложного объекта в целом, то точность аппроксимации виртуальной модели объекта ее оригиналу будет наивысшей. Для синтеза сложных рельефов земной поверхности и фоновых сюжетов рационально использовать анимационные системы, например, такие как 3 DStudioMax . В современных САПР твердотельная 3 D -модель объекта конвертируется в полигональную модель, представляющую собой конечную совокупность однотипных плоских элементарных отражателей с определенным набором электродинамических и статистических свойств, количество и форма которых определяется разработчиком.

Одной из известных расчетных методик, которые основаны на использовании фацетного описания геометрии цели, является методика Н.Юсефа [5] и ее реализация в виде программы RECOTA , которая использует метод физической теории дифракции (ФТД) на основе триангуляционной модели сложной цели, полученную средствами САПР. Однако эта модель предназначена лишь для расчетов характеристик рассеяния целей в дальней зоне, что неприемлемо для анализа входных сигналов СБРЛ. Кроме того, эта методика не учитывает сложных электрофизических структур на поверхности цели. К современным разработкам электромагнитных полей рассеяния сложных целей в ближней зоне локации следует отнести С patch technology [6], использующей метод «флуктуирующих» лучей ( shooting and bouncing rays ) на основе полигональных моделей 3- D объектов. В других работах для решения задач рассеяния электромагнитных полей рассеяния сложных объектов используются точные методы, такие как быстрый многополюсный метод [7] и метод конечных элементов [8], основанные на использовании пространственной триангулированной сетки внешней поверхности объекта. В работе [9] предложена модель, которая позволяет вычислять характеристики рассеяния целей, заданных в виде полигональных моделей, в ближней зоне локации для идеально проводящих целей, не учитывая при этом произвольного характера поляризации антенны. В качестве других недостатков модели [9] следует отметить отсутствие учета вкладов подстилающей поверхности и пассивных помех, а также невозможность вычисления полей рассеяния целей в случае сложных нестационарных воздействий на траектории движения.

Известно что, совокупность объектов сложной пространственной конфигурации и подстилающая поверхность образуют радиолокационную сцену [10], схема бистатической локации которой в ближней зоне приведена на рис. 1. Предполагается, что все элементы радиолокационной сцены заданы на основе полигональных моделей, которые в свою очередь могут быть сформированы в различных САПР. При этом каждый конструктивный элемент радиолокационной сцены представлен в виде совокупности элементарных отражателей (ЭО), наделенных определенным набором электрофизических и статистических параметров, характеризующих его уникальные рассеивающие свойства.

Анализ процессов облучения, рассеяния и приема электромагнитных волн следует проводить применительно к модели информационного радиолокационного канала (РЛК) [11], элементами которого являются передающая система СБРЛ, трасса распространения зондирующего сигнала, радиолокационная сцена, трасса распространения отраженного сигнала, приемная система СБРЛ. В данной модели, без учета активных и пассивных помех, устанавливается функциональное соотношение между зондирующим сигналом СБРЛ и отраженным эхо-сигналом , содержащим информацию об измеряемых параметрах объекта локации [11]:

,

где — оператор передающего тракта СБРЛ, соответствующий преобразованию зондирующего сигнала в излучаемую электромагнитную волну, — оператор преобразования электромагнитного поля от апертуры приемной антенны СБРЛ до детектора, — оператор преобразования электромагнитного поля на трассе «передатчик- радиолокационная сцена», операторы — определяет преобразование электромагнитного поля на трассе «радиолокационная сцена – приемная антенна», — оператор радиолокационной сцены.

Для расчета электромагнитных полей рассеяния ЭО радиолокационной сцены в [3] были использованы методы физической оптики (ФО), физической теории дифракции (ФТД) и метода краевых волн (МКВ). В соответствии с формализации процесса рассеяния электромагнитных волн на элементах радиолокационной сцены на основе метода ФТД вектор напряженности электрического поля рассеяния этих источников может быть представлено как векторно-когерентная аддитивная композиция трех компонент [3]:

(3)

где — соответствует вкладу в общее рассеянное поле от гладких элементов радиолокационной сцены (в том числе и от подстилающей поверхности), вторая компонента — соответствует вкладу от острых кромок элементов сцены, — соответствует рассеянию при многократных переотражениях электромагнитных волн между элементами сцены (в том числе между элементами объектов и подстилающих поверхностей).

В соответствии с принципом ФТД каждая из компонент результирующего поля рассеяния (3) характеризуется аддитивно-интегральной формой представления:

где — вектор поверхностных источников возбуждения, — источники электромагнитного поля рассеяния на поверхности сцены, — облучаемая часть поверхности объекта.

В данной статье на основе полигональной модели радиолокационной сцены [12] предложена новая математическая модель электромагнитных полей рассеяния в ближней зоне локации. Основные методические положения этой модели электромагнитных полей рассеяния сложных сцен на основе полигональных моделей приведены в [12]. Данная модель основана на формализации результирующего рассеянного поля в форме (1), (2), т.е. в качестве рассеивающих элементов рассматриваются плоские элементы гладкой части сцены и острые кромки. В качестве основной задачи будем рассматривать адаптацию данной математической модели к условиям ближней зоны радиолокации при облучении сцены сложными нестационарными воздействиями, а также с учетом взаимных перемещений СБРЛ и участков сцены на относительной траектории движения. С учетом того, что импульсная СБРЛ характеризуется определенным разрешением по дальности (рис. 1) представляет интерес анализ методов расчета импульсной ЭПР облучаемого участка радиолокационной сцены и импульсной характеристики сцены, характеризующей распределение амплитуды отраженного сигнала в каждом канале дальности СБРЛ. Для описания рассеивающих свойств сцены при облучении ее нестационарными во времени волновыми процессами применяли спектральный метод. Эффект трансформации вектора поляризации антенны в ближней зоне локации учитывался на основе разработанной модели, учитывающей произвольную поляризацию антенн СБРЛ.

Видео:Особенности распространения радиоволн [ РадиолюбительTV 16]Скачать

2. Формализация процесса рассеяния электромагнитных волн сложными радиолокационными сценами на основе их полигональных моделей

Полигональная модель радиолокационной сцены, используемая для описания процесса электромагнитного взаимодействия СБРЛ и радиолокационной сцены, является двухуровневой моделью. В качестве модели первого уровня рассматривается виртуальная (математическая) модель сцены. Эта модель представляет собой композицию примитивов, состав которых для современных автоматизированных систем предельно широк. Однако, такие модели помимо фиксированного набора примитивов, включают в свой состав средства, позволяющие с помощью преобразований из простейших примитивов создавать сложные неканонические поверхности. В современных САПР класс операций преобразования примитивов таков, что позволяет с инженерной точностью создать виртуальный образ практически любого фоноцелевого сюжета. В качестве примера на рис. 2 и 3 приведены виртуальные модели истребителя F -117 (среда Pro / En gineer ) и участка рельефа произвольной формы (среда 3 DStudioMax ).

Однако непосредственное использование модели первого уровня в задачах синтеза входных воздействий СБРЛ оказывается невозможным из-за непреодолимых проблем формализации процесса рассеяния электромагнитных волн на сложной поверхности радиолокационной сцены. Поэтому, в состав наиболее мощных САПР входят процедуры, позволяющие аппроксимировать поверхность сложной виртуальной модели в модель второго уровня, состоящей из простейших примитивов — полигонов. Другими словами, модель второго уровня и есть полигональная модель, используемая при проведении расчетов входных воздействий СБРЛ. Полигональная модель формируется на основе конвертации виртуальной модели сцены в текстовый файл, содержащий информацию о всех полигонах и острых кромках элементов сцены. При формировании полигональной модели объекта и конвертации ее в текстовый формат САПР решает наиболее трудоемкую задачу аналитического описания сложных поверхностей образующих объект. Количество элементов полигональной модели определяется как оптимум между ресурсами вычислительных средств и требуемой точности аппроксимации элементов сцены.

Современные САПР описывают внешнюю поверхность сцены в виде триангулированной сетки, т. е. в качестве базовых пространственных элементов полигональной модели используются плоские треугольные пластины, определенным образом состыкованные друг с другом. Пространственная конфигурация острых кромок определяется взаимным расположением образующих ее треугольников. В качестве примера на рис. 4 и 5 приведены полигональные модели ракеты АР-24 и истребителя F 117, сформированные в среде Pro / Engineer .

Плоский треугольный элемент описывается тремя вершинами, лежащими на поверхности объекта ( P ₁, P ₂, P ₃) и вектором внешней нормали к плоскости. Координаты вершин плоского треугольного элемента и координаты вектора нормали задаются в системе координат сцены. Уравнение плоскости треугольного полигона задается в виде известного соотношения где — направляющие косинусы внешней нормали, — расстояние от начала системы координат до плоского треугольного элемента. Острые кромки элементов сцены образуются в результате изломов гладкой поверхности. В структуре полигональной модели острые кромки образуются на основе образующих гладкую поверхность плоских треугольников. В качестве параметра геометрической конфигурации кромки используется внешний пространственный угол между треугольными пластинами, образующими кромку , где — вектор нормали к плоскости первого треугольника, — вектор нормали к плоскости второго треугольника.

Следует отметить, что современные системы САПР конвертируют два типа кромок. Первый тип представляет собой реальные кромки, образуемые в результате действительно имеющего место излома гладкой поверхности объекта. Другой тип кромок является результатом наложения плоской треугольной сетки на гладкую поверхность объекта и образования так называемых «мнимых» изломов. Такие кромки называются «мнимыми» («виртуальными») и при проведении расчетов не используются.

Для эффективного использования полигональной модели при решении радиолокационных задач формируется универсальная структура данных элементов полигональной модели. Описание элементов полигональной модели осуществляется с использованием с объектно-ориентрованных структур. основных геометрических примитивов: структура “ point ”, структура » triangle » и структура » edge «. Подробное описание структуру данных приведено в [10].

Источники полей рассеяния электромагнитных волн, распределенные на элементах полигональной модели в приближении ФТД, имеют смысл лишь в тех областях на поверхности сцены, которые освещены со стороны передатчика СБРЛ и не затеняются со стороны приемника СБРЛ. Поэтому, алгоритмы анализа условий затенения и маскировки элементов полигональной модели являются одним из ключевых моментов данной геометрической модели. Анализ условий затенения и маскировки элементов полигональной модели осуществляется относительно положения приемо-передающей системы СБРЛ, заданного в системе координат сцены.

Фацетное представление полигональной модели радиолокационной сцены позволяет представить сферическую электромагнитную волну вблизи облучаемого участка сцены в виде суперпозиции локально плоских волн (рис. 6). При этом пространственная сетка внешней поверхности объекта формируется таким образом, чтобы падающие на элементы полигональной модели электромагнитные волны можно было рассматривать как локально плоские. Для того чтобы падающую на элемент полигональной модели электромагнитную волну считать плоской, его линейный размер должен удовлетворять критерию дальней зоны:

,

где — характерный линейный размер m-го элемента полигональной модели, — расстояние между фазовым центром антенны СБРЛ и m-м элементом.

Облучающая элемент полигональной модели локально плоская электромагнитная волна наводит на его поверхности электрический и магнитный токи , которые являются вторичными источниками электромагнитных волн, рассеянных в направлении приемной системы СБРЛ. Вектор напряженности поля рассеяния полигона определяется в соответствии с интегральным представлением (4) на основе принципа ФТД. Задача рассеяния электромагнитных волн на элементе полигональной модели объекта решается отдельно для плоской волны с линейной поляризацией, вектор поляризации которой определяется в зависимости от поляризационной модели передающей антенны (линейная, круговая, эллиптическая).

В соответствии с формализацией (3-4) дифракционного электромагнитного поля рассеяния сцены, заданной своей полигональной моделью, величина результирующей напряженности поля рассеяния, принятого в апертуре приемной антенны СБРЛ, представляется в виде суперпозиции трех скалярных величин:

(5)

Первая компонента в соотношении (5) представляет собой величину результирующей напряженности электрического поля рассеяния всех плоских треугольных элементов, образующих полигональную модель объекта:

где — вектор напряженности электрического поля рассеяния m -го треугольника полигональной модели, — вектор поляризации приемной антенны СБРЛ в направлении на треугольник, N _{tr .} – количество облучаемых треугольников полигональной модели.

Вторая составляющая в соотношении (5) является результирующей напряженностью поля рассеяния острых кромок полигональной модели:

где — вектор напряженности электрического поля рассеяния m -й острой кромки полигональной модели, — вектор поляризации приемной антенны СБРЛ в направлении на острую кромку, N_ed. – количество облучаемых острых кромок полигональной модели

Составляющие (6, 7) определяются на основе интегрирования токов, возбуждаемых основным полем облучения антенны СБРЛ на треугольниках и острых кромках соответственно. При этом третья компонента поля (5) определяется в результате суперпозиции полей рассеяния треугольников, для которых источники возбуждения вторичных волн наводятся за счет многократных переотражений от других треугольников полигональной модели:

В соотношении (8) представляет собой вектор напряженности поля рассеяния треугольника, токи возбуждения которого наведены за счет переотражения от другого треугольника, а – количество треугольников, участвующих в переотражениях.

В дальнейших рассуждениях будем рассматривать все элементы полигональной модели (треугольники и кромки) как элементарные отражатели (ЭО). Поэтому не теряя общности рассуждений, можно представить величину напряженности результирующего поля рассеяния объекта (5) в виде суперпозиции полей рассеяния всех ЭО полигональной модели сцены:

где m – индекс элементарного отражателя (ЭО), — величина напряженности электрического поля рассеяния m-го ЭО принятого в апертуре приемной антенны СБРЛ, — общее количество ЭО, принимающих участие в рассеянии электромагнитных волн.

Таким образом, получены расчетные соотношения для вычисления величины напряженности поля рассеяния сцены, находящейся в ближней зоне локации (9). Для более детального анализа процесса электромагнитного взаимодействия СБРЛ и сцены необходимо рассмотреть математическую модель излучения антенны с ближней зоне локации и методы расчета электромагнитных полей рассеяния элементов полигональных моделей.

Видео:Антенны. Как работают антенны простыми словами. ч.7.2- зоны ФренеляСкачать

3. Поляризационная модель электромагнитного поля рассеяния объекта в ближней зоне локации

Для анализа процесса электромагнитного взаимодействия СБРЛ и сцены необходимо сформировать математическую модель антенны СБРЛ с требуемой диаграммой направленности и поляризационной характеристикой. Одним из важнейших параметров антенны СБРЛ является ее векторная нормированная характеристика направленности [13] , полностью определяющая угловое распределение и все поляризационные и фазовые свойства электромагнитного поля в дальней зоне антенны. В самом общем случае векторная комплексная характеристика направленности состоит из произведения трех сомножителей, описывающих соответственно амплитудную, фазовую и поляризационную структуру дальнего поля антенны [13]:

(10)

где — амплитудная характеристика поля, — фазовая характеристика поля, — поляризационная характеристика поля, .

Для описания характеристик антенны, входящих в соотношение (10) вводится система координат антенной системы (рис. 7), включающая три вектора единичной амплитуды: — вектор, определяющей направление на максимум излучения (приема) антенны; — вектора поляризационного базиса антенны. Считается, что все три вектора взаимно ортогональны, причем вектор соответствует оси x системы координат антенны, вектор соответствует оси y данной системы координат, а вектор — соответствует оси z (рис. 7). Ориентация осей системы координат (рис. 7) в пространстве определяется для заданного положения антенны СБРЛ относительно объекта. Считается, что плоскость системы координат антенны xoy – угломестная (меридианальная), а плоскость xoz – азимутальная (экваториальная). Поляризационный базис антенны лежит в плоскости yoz . Угол отсчитывается в азимутальной плоскости, а угол отсчитывается в угломестной плоскости. При этом характеристики поля антенны (10) задаются в системе координат антенны в зависимости от углов (,).

Вещественный сомножитель в (10) представляет собой амплитудную характеристику (диаграмму) направленности по полю, нормированную таким образом, что max()=1. Диаграмма направленности антенны (ДНА) может быть получена как расчетным, так и экспериментальным путем. Векторный сомножитель в (10) представляет собой единичный вектор поляризации с двумя компонентами, ориентированными по направлениям единичных базисных ортов и в системе координат антенны (рис. 7):

(11)

, — компоненты вектора поляризации, причем .

Компоненты , в (11) показывают относительное содержание вертикальной и горизонтальной составляющих вектора напряженности электрического поля в дальней зоне антенны, а — определяет фазовый сдвиг между этими компонентами. Предполагается, что ось z (составляющая по ) соответствует главной поляризации антенны СБРЛ. Второй компонент вектора поляризации, ортогональный главному компоненту, считается кроссполяризационной составляющей поляризации антенны. Компонента главной поляризации полагается вещественной с амплитудой , а компонента кроссполяризационной составляющей считается комплексной .

Антенная система СБРЛ способна излучать и принимать электромагнитные волны трех типов поляризаций: эллиптическая, круговая, линейная. В зависимости от типа поляризации компоненты , будут вычисляться по-разному. Тип поляризации зависит от значений геометрических параметров эллипса поляризации (рис. 8), а именно от коэффициента эллиптичности r , который представляет собой отношение малой и большой главных осей эллипса (рис. 8) и угла ориентации большой оси эллипса в поляризационном базисе. Эллипс поляризации представлен на плоскости, касательной к сферическому фронту волны в окрестности выбранной точки наблюдения.

Для эллиптической поляризации коэффициент эллиптичности может принимать любое значение в диапазоне <, >, а угол поворота ограничен значениями . Принято приписывать величине r знак плюс при правом вращении , а минус – при левом вращении. Для эллиптической поляризации компоненты вектора (11) вычисляются из следующих соотношений [13]:

,,.

Для правой круговой поляризации коэффициент эллиптичности должен принимать значение r =1, а для левой – соответственно r =-1. Угол поворота при этом должен лежать в пределах . В случае круговой поляризации компоненты вектора (11) определяются следующим образом:

,, , если r =1;

,, , если r =-1, где .

Для формирования линейной поляризации электромагнитной волны коэффициент эллиптичности должен принимать значение r =0. При этом угол b определяет ориентацию вектора напряженности электрического поля в поляризационном базисе антенны (рис. 8). Угол поворота b для линейной поляризации может принимать любое значение из диапазона . При линейной поляризации составляющие вектора (11) зависят только от угла b и определяются из соотношений:, .

Соотношение для вектора поляризации антенны (11) справедливо лишь для дальней зоны локации и соответствует направлению на максимум ДНА, когда углы поворота сферической системы координат . В ближней зоне локации возникает эффект трансформации поляризационного базиса антенны (рис. 7). При этом в боковом направлении излучения (приема) возникает локальный поляризационный базис в направлении локального направляющего вектора . Вектор характеризует поляризацию антенны в меридианальной плоскости системы координат (рис. 7), а вектор соответственно в экваториальной плоскости. По аналогии с основным поляризационным базисом антенны вектор определяет направление главной поляризации в локальном базисе, а вектор соответственно кроссполяризационной компоненты. Представление вектора поляризации антенны в локальном поляризационном базисе связано с перераспределением амплитуд составляющих основного поляризационного базиса антенны по боковым направлениям излучения (приема) и выглядит следующим образом:

(12)

(13)

(14)

где , — составляющие ортов локального поляризационного базиса антенны.

При вычислении напряженности поля рассеяния ЭО считается, что падающая на отражатель и отраженная от него электромагнитные волны считаются плоскими, а излучение и прием ведутся на линейной поляризации. Для вычисления напряженности поля рассеяния отражателя необходимо сформировать ортогональный базис падающей на отражатель плоской волны и локальный базис приемной антенны, соответствующий приему плоской волны, рассеянной отражателем. В соответствии с поляризационной моделью антенны (12-14) структура базиса плоской волны содержит единичный вектор в направлении на данный ЭО и два ортогональных единичных вектора, которые характеризуют поляризацию волны . В соответствии с (12) вектору линейной поляризации соответствует амплитуда , а вектору соответствует компонента , которые вычисляются из (13-14) соответственно.

В соответствии с общепринятыми представлениями [2] вектор напряженности поля плоской электромагнитной волны, падающей на ЭО, находящийся на расстоянии от передающей антенны определяется следующим образом:

где P_i – мощность сигнала, излучаемого передающей системой, D_i – КНД передающей антенны в направлении максимума излучения, Z₀=120 p Ом – волновое сопротивление воздуха, — расстояние между фазовым центром антенны и началом системы координат ЭО, — круговая частота электромагнитных колебаний, — векторная характеристика направленности передающей антенны в направлении на ЭО.

Учитывая представление векторной характеристики направленности антенны в виде произведения трех сомножителей (10), а также соотношение для вектора поляризации падающей на ЭО плоской волны (12) напряженность поля (15) вблизи ЭО удобно записывать в матричном виде:

, (16)

где F_im – значение функции направленности передающей антенны в направлении на m-й ЭО, — начальная фаза передающей антенны.

Вектор напряженности поля, рассеянного ЭО, в точке расположения приемной антенны СБРЛ также определяется в матричном виде:

где — поляризационная матрица рассеяния (ПМР) ЭО, — вектор-столбец компонент вектора напряженности рассеянного поля в направлении поляризационных ортов и , — расстояние между ЭО и фазовым центром приемной антенны.

ПМР описывает рассеивающие свойства ЭО в зависимости от поляризационных характеристик передающей и приемной антенн. При этом считается, что индекс i соответствует облучающей волне, а s – вектору поляризации приемной антенны. Каждый элемент ПМР (18) представляет собой комплексный коэффициент отражения ЭО [11], который определяется из следующего соотношения:

где — величина напряженности поля рассеяния ЭО, которая вычисляется для случая, когда излучение и прием ведутся на линейной поляризации.

В соответствии с (19) комплексный коэффициент отражения ЭО выражается в [м] и не зависит от амплитуды электромагнитной волны, падающей на ЭО, а также от расстояния до фазового центра передающей антенны. При этом комплексный коэффициент отражения находится в функциональной зависимости от геометрических размеров ЭО, его электродинамических параметров, а также от его ориентации в пространстве относительно передающей и приемной антенн СБРЛ. В зависимости от типа ЭО (треугольник или острая кромка), а также в зависимости от происхождения источников электромагнитного поля на поверхности ЭО комплексный коэффициент отражения (23) будет вычисляться с использованием различных методов.

Величина напряженности поля рассеяния m-м ЭО, принятого в апертуре приемной антенны, определяется в результате скалярного произведения вектора напряженности рассеянного поля вблизи приемной антенны (17) на вектор поляризации приемной антенны (12) в направлении на данный ЭО:

(20)

После подстановки в (20) выражений для составляющих вектора напряженности рассеянного поля вблизи антенны получим окончательное выражение для вычисления величины напряженности поля рассеяния m-го ЭО, принятого в апертуре приемной антенны СБРЛ:

(21)

(22)

С использованием соотношения (21), для каждого ЭО вычисляется величина напряженности поля рассеяния, принятого в апертуре приемной антенны, а затем подставляется в (9) для получения величины напряженности результирующего дифракционного поля рассеяния всей радиолокационной сцены:

Таким образом, на основе поляризационной модели поля рассеяния радиолокационной сцены, заданной своей полигональной моделью, получено соотношение для расчета величины результирующей напряженности электрического поля рассеяния, принятого в апертуре приемной антенны СБРЛ.

Видео:Зоны Френеля для трехсантиметровой волныСкачать

4. Анализ комплексных коэффициентов отражения элементов полигональных моделей

В соответствии с формализацией процесса рассеяния электромагнитных волн квазиоптического диапазона на сложных радиолокационных сценах (1,2) в качестве методологической основы при вычислении полей рассеяния наиболее рационально использовать методы ФО и ФТД применительно к полигональной модели сцены.

Для вычисления комплексного коэффициента отражения плоского треугольника полигональной модели, схема радиолокации которого приведена на рис. 9, был использован метод ФО, согласно которому поле на поверхности треугольника определяется в результате векторной суммы падающего на плоскость поля и поля отраженного от плоскости треугольника по законам геометрической оптики (ГО). Выражение для комплексного коэффициента отражения треугольника, полученное на основе метода ФО и соотношения (19) имеет вид:

(24)

(25)

(26)

(27)

, , , ,

, , ,

где — вектора локального базиса треугольника, <> – орты поляризационного базиса падающей волны, — вектор нормали к плоскости треугольника, — разностный направляющий вектор, — вершины треугольника, — коэффициенты отражения от плоскости треугольника для вертикальной и горизонтальной поляризаций, — проекция разностного вектора на плоскость треугольника, причем , () – вектор локального поляризационного базиса передающей (приемной) антенны.

Коэффициенты отражения вычисляются на основе метода ГО для треугольника, покрытого многослойным радиопоглощающим покрытием (РПП). Алгоритм расчета организуется на основе ступенчатого пошагового вычисления коэффициента отражения, начиная с последнего слоя покрытия [14]. При этом если поверхность треугольника не содержит РПП, то представляют собой коэффициенты отражения Френеля для треугольника из однородного материала. Выражение (24) получено с использованием метода Гордона, согласно которому поверхностный интеграл источников на плоскости треугольника заменяется криволинейным интегралом по контуру, ограничивающему треугольник.

Проблема оценки вкладов многократных переотражений между треугольниками решается на основе комбинированного применения методов геометрической оптики (ГО) и ФО. Физический смысл решения заключается в том, что поле, падающее на некоторый треугольный элемент, не рассеивается в окружающее пространство, а переотражается по законам ГО в направлении другого треугольного элемента и служит источником возбуждения на нем вторичных электромагнитных волн (рис. 10). Эти электромагнитные волны, рассеиваясь в направлении СБРЛ, создают в апертуре приемной антенны дополнительное электромагнитное поле. Основной задачей является определение амплитуды и вектора поляризации электромагнитной волны переотраженной с первого треугольного элемента на второй. В данной статье рассматривается математическая модель учета лишь двукратных переотражений волн между треугольниками.

При разработке математической модели электромагнитного взаимодействия треугольников, возникающего за счет многократных переотражениях, использовалась технология «флуктуирующих лучей», или « shooting and bouncing rays » ( SBR ), приведенная в [15]. В соответствии с основными положениями данной методикой расчета для вычисления комплексного коэффициента отражения плоского треугольника, на котором вторичные источники электромагнитного поля наведены в результате воздействия других треугольников, получено следующее соотношение:

(29)

, , , , ,,

где — расстояние от фазового центра P приемной системы до начала координат треугольника T ₂, — проекция разностного вектора на плоскость второго треугольника, — единичный направляющий вектор рассеянной от треугольника T ₂ волны, проведенный из точки в фазовый центр антенной системы P , — определяются для второго треугольника из соотношений (25-28), — расстояние между средней точкой P треугольника T ₁ и точкой пересечения направляющего вектора с плоскостью второго треугольника, — отношение площадей треугольников.

При выводе соотношения (29) не был учтен фактор расходимости лучевой трубки при переотражениях волн по причине значительного усложнения алгоритма расчета переотражений и значительных временных затрат для сцен, содержащих большое количество треугольников. Неизбежная погрешность, возникающая при этом в результатах вычислений двукратных переотражений должна компенсироваться повышением качества полигональной сетки, описывающей поверхность сцены.

В случае если плоский треугольный элемент полигональной модели сцены является частью подстилающей поверхности, его комплексный коэффициент отражения определяется из соотношения:

,

где — удельная ЭПР элемента подстилающей поверхности, — расстояние от центра треугольника до приемной системы СБРЛ, — случайная фаза рассеянного поля, распределенная равномерно в пределах [0..2 p ], S_m – площадь треугольника.

Методы вычисления удельной ЭПР различных типов подстилающих поверхностей подробно изложены в [16].

Для вычисления полей рассеяния острых кромок элементов сцены используются методы краевых волн и ФТД. Комплексный коэффициент отражения острой кромки (рис. 11), полученный на основе применения этих методов, представлен в следующем виде [10]:

,

,

где , — пространственные углы между направляющими векторами , и вектором , () – вектор локального поляризационного базиса передающей (приемной) антенны.

В [17] показано, что при моностатической локации амплитуды краевых источников возбуждения F и G рационально определять через коэффициенты дифракции в форме Уфимцева.

Для обобщения перечисленных математических моделей комплексных коэффициентов отражения элементов полигональных моделей в рамках единой методики цифрового моделирования используется разработанный ранее объектно-ориентированный метод исследования электромагнитных полей рассеяния ЭО 19. Применение объектно-ориентированной технологии для цифрового моделирования процесса рассеяния электромагнитных волн на ЭО полигональной модели предоставляет значительные преимущества в универсальности и эффективности методики расчета по сравнению с уже известными методами.

В соответствии концепцией объектно-ориентированного программирования методы расчета электромагнитного поля рассеяния каждого элемента (треугольник, кромка) представляются в форме объектно-ориентированных классов. Каждый класс содержит приватные данные, представляющие собой параметры данного типа отражателя и методы оценки его поля рассеяния. В соответствии с описанными выше математическими моделями рассеяния радиоволн на различных типах отражателей формируется два класса-метода, характеризующих рассеивающие свойства этих отражателей: класс-метод треугольного элемента и класс-метод острой кромки. Все классы-методы являются наследниками двух базовых классов, в которых формируются вектора базисов падающей и отраженной волн, а также электродинамические параметры элемента полигональной модели в зависимости от длины волны . Объект класса-метода создается на этапе расчета и представляет собой процесс взаимодействия плоской электромагнитной волны с элементарным отражателем, обладающим определенной совокупностью электродинамических параметров. Созданный объект класса-метода позволяет вычислить комплексный коэффициент отражения соответствующего ЭО в процессе суммирования полей от всех элементов данного типа.

Видео:Inside Wireless: зоны ФренеляСкачать

5. Математическая модель энергетических характеристик входных сигналов СБРЛ и характеристик рассеяния объектов в ближней зоне локации

В качестве энергетической характеристики входного сигнала СБРЛ используется его мощность, выделяемая в согласованной нагрузке приемной антенны. При этом основной задачей является построение математической модели для вычисления мощности сигнала, отраженного от сцены, заданной своей полигональной моделью. Методологической основой такой модели является формализация процесса рассеяния электромагнитных волн от радиолокационной сцены в виде (23). Для СБРЛ, работающей в непрерывном режиме излучения радиоволн мощность входного сигнала, выделяемая в согласованной нагрузке антенны, определяется из следующего соотношения [13]:

где — амплитуда напряжения входного сигнала СБРЛ, — сопротивление излучения антенны.

Результирующее напряжение в нагрузке приемной антенны , возникающее от воздействия всех ЭО, образующих полигональную модель сцены, определяется по аналогии с (23) в результате когерентного суммирования парциальных напряжений, возникающих в нагрузке антенны от воздействия каждого ЭО:

(31)

где — напряжение, возникающее в нагрузке антенны от воздействия m-го ЭО.

Напряжение в согласованной нагрузке приемной антенны, полученное от воздействия m-го ЭО, определяется произведением величины напряженности его электрического поля рассеяния (21) на модуль действующей высоты антенны:

(32)

где h_a – модуль действующей высоты приемной антенны, – значение функции направленности приемной антенны в направлении на m-й ЭО, D_s – КНД приемной антенны в направлении максимума излучения.

С использованием соотношений (21, 30-33) результирующее напряжение возникающее в нагрузке приемной антенны СБРЛ от воздействия сцены в ближней зоне локации, определяется следующим образом:

где — результирующий коэффициент рассеяния объекта, выраженный в [1/м], — комплексный коэффициент отражения ЭО, который определяется из соотношения (22).

В результате подстановки выражения для расчета действующего значения входного напряжения (34) в (30) мощность входного сигнала СБРЛ, работающей в непрерывном режиме излучения, будет вычисляться на основе следующего соотношения:

Энергетические характеристики входных сигналов СБРЛ напрямую связаны с энергетическими характеристиками рассеяния радиолокационных сцен. В классической теории радиолокации в качестве энергетической характеристики рассеяния используется понятие ЭПР (2), которая определяется в дальней зоне излучения антенны. Очевидно, что для объекта, находящегося в ближней зоне излучения антенны, когда предел не выполняется, соотношение (2) не может быть использовано для вычисления ЭПР объекта. В этом случае ЭПР объекта будем определять из уравнения дальности радиолокации, которое имеет следующий вид [21]:

где P – мощность входного сигнала СБРЛ, R — расстояние между условной точкой сцены и фазовым центром антенны, () — значение функции направленности передающей (приемной) антенны в направлении на условную точку сцены.

Из уравнения (36) ЭПР объекта будет определяться мощностью отраженного от него сигнала, расстоянием до антенны и значениями функций направленности передающей и приемной антенн в направлении на объект:

В случае если облучаемый участок сцены имеет такой линейный размер L, что на расстоянии R до фазового центра антенны не выполняется критерий дальней зоны (1), то соотношение (38) будет определять ЭПР сцены в ближней зоне локации. После подстановки в (38) соотношений для вычисления мощности входного сигнала СБРЛ (36) получим для расчета ЭПР в ближней зоне локации следующее выражение:

Из соотношения (39) наблюдается зависимость ЭПР в ближней зоне от расстояния до антенны и от функции направленности передающей и приемной антенн.

Для участка сцены, находящегося в дальней зоне излучения антенны, когда расстояние от условной точки сцены до фазового центра приемной антенны удовлетворяет критерию дальней зоны (1) выполняются следующие условия:

• Расстояния от всех ЭО до фазового центра антенны совпадают с расстоянием до условной точки сцены, т. е. ;
• Значения функции направленности передающей (приемной) антенны в направлении на все ЭО полигональной модели совпадают с значением функции направленности в направлении на условную точку сцены, т. е. , .

С учетом перечисленных условий получим из (39) ЭПР сцены, заданной своей полигональной моделью, в дальней зоне локации:

В отличие от ЭПР в ближней зоне, ЭПР сцены, находящейся в дальней зоне (40) не зависит от расстояния и от функции направленности антенны. В соответствии с выражением (23) модуль напряженности электрического поля рассеяния радиолокационной сцены в дальней зоне локации можно определить в следующем виде:

Аналогично в соответствии с (16) величина модуля напряженности электрического поля, облучающего сцену в направлении на ее условную точку, определяется из выражения:

После подстановки выражения (42) в (41) получим величину квадрата модуля результирующей суммы комплексных коэффициентов отражения элементов сцены в следующем виде:

Очевидно, что после подстановки (43) в соотношение (40) выражение для расчета ЭПР в дальней зоне локации приобретает вид, аналогичный формуле (2):

Таким образом, показано, что при переходе из ближней зоны в дальнюю зону локации, выражение для расчета ЭПР сцены в ближней зоне (39) приводится к классической формуле ЭПР точечного объекта в дальней зоне локации.

Отдельной проблемой является вычисление мощности отраженного от сцены сигнала для СБРЛ, работающей в импульсном режиме излучения. В этом случае на конечный результат будет оказывать влияние форма огибающей сигнала , поступающего на вход приемной антенны, т. к. радиолокационные цели изменяют форму и характер облучающих их сигналов при рассеянии. Для импульсной СБРЛ входное воздействие представляет собой отклик сцены на воздействие вида:

,

где f₀ – частота несущего колебания, j ₀ – начальная фаза несущей, t — длительность импульса, b – крутизна импульса, g — параметр частотной модуляции, T – интервал наблюдения.

Для вычисления отклика от сцены используется спектральный подход, основанный на применении преобразования Фурье в комплексной форме, когда зондирующий импульс представляется в частотной области в виде дискретного спектра значений:

,

где n — индекс составляющей спектра, k — индекс отсчета сигнала, N – количество отсчетов сигнала во временной области, f_n – спектральная составляющая частоты.

В соответствии с представлением зондирующего сигнала (45) напряженность поля, падающего на m-й ЭО, также представляет собой дискретный спектр значений на различных частотах:

где — значение амплитуды спектральной составляющей зондирующего сигнала, — волновое число в зависимости от n-й составляющей частотного спектра, а в качестве величины P_i принимается пиковая мощность передающей системы СБРЛ.

Спектральная зависимость напряженности поля рассеяния сцены, принятого в апертуре приемной антенны, выглядит следующим образом:

По аналогии с (34, 47) частотный спектр результирующего напряжения принятого в нагрузке приемной антенны СБРЛ определяется следующим образом:

где c – скорость света.

Таким образом, отклик сцены, представляющий собой входной радиосигнал СБРЛ, определяется с использованием обратного преобразования Фурье от частотного спектра входного напряжения:

где k=0. N-1 – количество дискретных отсчетов входного сигнала, — дискретное значение времени в отклике, — значение модуля огибающей входного сигнала СБРЛ.

В результате подстановки в (49) значений спектра входного напряжения получим входной сигнал СБРЛ в следующем виде:

Мощность импульсного сигнала на входе СБРЛ также будет функцией от времени:

В качестве энергетической характеристики входного сигнала (49) будем считать среднюю мощность за время, равное длительности отраженного импульса:

где T – длительность сигнала, N=2f₀T – общее число дискретных отсчетов сигнала, — длительность отраженного импульса, — количество дискретных отсчетов сигнала в отраженном импульсе.

При локации сцен произвольными нестационарными воздействиями используют понятия частотной и импульсной характеристик объектов [11]. Частотная характеристика сцены определяется в результате отнесения спектра значений отклика сцены и воздействия в виде сферической волны, облучающей сцену. В данной статье будем использовать понятие нормированной частотной характеристики сцены [11], однозначно определяющей ЭПР сцены. В соответствии с (39, 48) нормированная частотная характеристика сцены определяется в виде спектра значений результирующего коэффициента рассеяния:

Нормированная импульсная характеристика сцены определяется на основе обратного преобразования Фурье от частотной характеристики (54) и представляет собой отклик сцены на воздействие d -функции:

Рассмотрим проблему вычисления ЭПР объекта при его локации импульсным сигналом. В традиционной радиолокации считалось, что на протяжении всего отраженного импульса значение ЭПР цели будет приблизительно постоянно. Но при короткоимпульсной локации так считать уже нельзя [22]. В этом случае ЭПР имеет колебательный характер, причем для более коротких импульсов размах колебаний будет возрастать. Кроме того, длительность отраженного импульса будет все более увеличиваться по сравнению с длительностью зондирующего. В этом случае возникает вопрос о том, что считать ЭПР объекта, т. к. пользоваться соотношениями (39, 40) уже не представляется возможным. В работе [22] установлено, что ЭПР представляет собой мощностную характеристику, которая должна определять среднюю величину мощности отраженного от цели сигнала. В связи с этим очевидно, что необходимо по аналогии с (52) усреднить ЭПР за время длительности отраженного импульса, получив среднюю ЭПР .

В соответствии с (39, 55) ЭПР сцены в каждый момент времени, при локации импульсным сигналом, будет определяться как квадрат модуля импульсной характеристики сцены:

(56)

где — модуль импульсной характеристики сцены в момент времени t_k.

Таким образом, импульсная ЭПР объекта определяется в результате усреднения ее огибающей (56) за время длительности отраженного импульса и вычисляется с использованием следующего соотношения:

где — количество дискретных отсчетов сигнала в отраженном импульсе.

При отражении от сцены импульс растягивается во времени по сравнению с зондирующим импульсом. При этом величина увеличения длительности отраженного от объекта импульса определяется из следующего соотношения:

,

где — расстояние от фазового центра антенны до наиболее ближней к антенне точке сцены, — расстояние от фазового центра антенны до наиболее дальней к антенне точке сцены, c – скорость света.

Таким образом, получены расчетные соотношения, позволяющие вычислять мощность отраженного от сцены сигнала для СБРЛ, работающей как в непрерывном, так и в импульсном режиме излучения. Кроме того, показано, что выражения для расчета ЭПР в ближней зоне локации при переходе объекта в дальнюю зону преобразуется в классическое выражение для вычисления ЭПР сосредоточенного объекта. Получены расчетные соотношения для вычисления ЭПР сложной сцены в ближней зоне локации для монохроматического и импульсного зондирующих воздействий.

Видео:Ближняя зона радиоантенны и трение нанообъектовСкачать

6. Математическая модель спектра доплеровских частот входных сигналов СБРЛ

Одной из основных особенностей функционирования СБРЛ является эффект возникновения спектра доплеровских частот отраженного сигнала, вызванный взаимным перемещением СБРЛ и элементов сцены. Если СБРЛ работает в непрерывном режиме излучения, то несущая частота излучения f₀ трансформируется в спектр шириной . Подобная трансформация несущей частоты является результатом того, что сцена состоит из совокупности отражающих элементов, разнесенных в пространстве и перемещающихся с разными скоростями относительно СБРЛ. Наличие в спектре отраженного сигнала полосы доплеровских частот свидетельствует о том, что отраженный сигнал изменяется по более сложному закону, чем излученный. Если СБРЛ излучает непрерывный монохроматический сигнал частоты f₀, то величина полностью характеризует ширину спектра отраженного сигнала. Поскольку сигнал, излучаемый СБРЛ, который работает в импульсном режиме излучения, имеет широкую полосу частот , то после отражения такого сигнала произойдет трансформация всех его частотных составляющих. В данной статье ставится задача качественного анализа данного явления, поэтому в целях простоты ограничимся рассмотрением спектра доплеровских частот при отражении монохроматического сигнала. Выясненные в результате подобного анализа закономерности будут проявляться и в случае сигналов более сложной формы, хотя количественные соотношения между основными параметрами изменяться и станут сложнее.

Предположим, что антенна СБРЛ облучает некоторую цель на радиолокационной сцене, заданную своей полигональной моделью, и движущейся в направлении вектора скорости . При этом СБРЛ расположена на носителе, который движется в направлении вектора . Тогда характер взаимного движения СБРЛ и цели определяется вектором относительной скорости . Будем считать, что вектор относительной скорости приложен в фазовом центре антенны СБРЛ. Вследствие взаимного перемещения СБРЛ и цели доплеровский сдвиг частоты сигнала, отраженного от m-го ЭО определяется в результате следующего соотношения:

где — единичный вектор, проведенный из фазового центра антенны в характерную точку ЭО.

В результате изменения m-м ЭО несущей частоты зондирующего сигнала, напряжение, поступающее на вход СБРЛ от воздействия данного ЭО, будет вычисляться на основе (34) из следующего соотношения:

где — волновое число, вычисленное с учетом доплеровского сдвига частоты.

Совокупность значений напряжения сигналов (59), отраженных от всех ЭО () представляет собой частотный спектр флуктуаций, вызванных эффектом взаимного перемещения цели и СБРЛ. Для оценки ширины спектра флуктуаций необходимо определить минимальный и максимальный доплеровские сдвиги частоты ЭО полигональной модели цели. Пусть условная точка цели находится под углом к вектору относительной скорости. Углы между вектором относительной скорости и крайними элементами цели, определяющими ее габариты, вычисляются из соотношений:

, .

Вследствие этого доплеровские сдвиги несущей частоты сигналов, отраженных от крайних элементов цели будут определяться следующим образом:

, , где — модуль вектора относительной скорости.

Остальные ЭО полигональной модели дадут отраженные сигналы, у которых несущие частоты будут иметь доплеровские сдвиги, лежащие в пределах от до . Таким образом, несущие частоты сигналов, отраженных от отдельных элементов цели, занимают спектр значений от до шириной:

Из (60) следует, что ширина спектра доплеровских частот пропорциональна несущей частоте f₀ и существенно зависит от угла , угловых размеров цели и скорости относительного движения ракеты и цели. В [23] установлена связь ширины спектра флуктуаций (60) и времени корреляции входного сигнала . С увеличением размера цели увеличивается ширина спектра доплеровских частот и уменьшается время корреляции, что связано с увеличением числа ЭО, участвующих в формировании результирующего сигнала. Поэтому при тех же перемещениях происходит перераспределение фаз и амплитуд большего числа сигналов, что ведет к ускорению флуктуаций результирующей амплитуды. Связь между спектром доплеровских частот отраженного сигнала и размерами цели может быть использована для определения ее габаритов.

Видео:Зоны ФренеляСкачать

7. Анализ результатов цифрового моделирования входных воздействий СБРЛ и энергетических характеристик рассеяния сложных объектов в ближней зоне локации

Для решения задачи цифрового моделирования входных воздействий СБРЛ в МГТУ им. Н.Э. Баумана 19 был разработан комплекс алгоритмов и прикладных программ, позволяющий вычислять мощность отраженного от сцены сигнала, а также характеристики рассеяния при различных условиях локации. В разработанной программе инициализируются параметры СБРЛ, условия локации радиолокационной сцены, а также параметры траектории относительного движения СБРЛ относительно элементов сцены. Кроме того, в структуру программы входят блоки формирования полигональных моделей сцены и анализа затенений и маскировки элементов полигональных моделей. Расчетный блок программы обеспечивает непосредственное вычисление мощности отраженного от сцены сигнала на каждом кадре траектории движения СБРЛ. При этом вычисление комплексных коэффициентов отражения элементов полигональных моделей осуществляется на основе рассмотренного выше объектно-ориентированного метода.

Для идентификации результатов расчета ЭПР, полученных на основе цифрового моделирования, с точными решениями задачи дифракции, представленными в виде аналитических соотношений, наиболее рационально использовать объекты простой геометрической формы, которые носят название эталонных отражателей. Результаты расчета ЭПР с использованием таких соотношений имеют достаточно высокую степень совпадения с результатами экспериментальных исследований для эталонных отражателей. В связи с этим на основе сравнительного анализа ЭПР эталонных отражателей, полученных в результате цифрового моделирования и на основе общеизвестных аналитических соотношений, можно сделать вывод о правильности вычисления характеристик рассеяния методами цифрового моделирования.

Наиболее простым с точки зрения пространственной конфигурации объектом является сфера, поверхность которой не имеет изломов. В данной статье произведен расчет ЭПР идеально проводящей сферы r =25.4 см, полигональная модель которой сформирована в среде 3 DStudioMax и образована из 32000 плоских треугольных элементов, причем максимальный размер треугольного элемента не превышает l =8.6 мм.

В соответствии с общепринятыми представлениями ЭПР идеально проводящей сферы в дальней зоне, полученное аналитическим путем, определяется из соотношения . Кроме того, в работе [9] приведены расчетные зависимости ЭПР сферы в ближней зоне локации. На рис. 12 приведены зависимости моностатической ЭПР сферы от расстояния R между центром сферы и фазовым центром приемной антенны. При вычислении зависимостей ЭПР, представленных на рис. 12 поляризация антенн СБРЛ принималась согласованной вертикальной, а длина волны принималась равной l = 3см. Диапазон изменения расстояния между сферой и антенной принимался равным , а шаг изменения расстояния соответственно D R =1 см. Значение функции направленности антенн по всем направлениям принималось равным F =1.

В заданном диапазоне дальностей сфера радиусом r =25.4 см находится в ближней зоне локации по отношению к антенне. В этом случае электромагнитная волна, облучающая сферу, имеет сферический фронт. На рис. 12 сплошной кривой обозначена зависимость ЭПР, полученная в результате цифрового моделирования на основе соотношения для ЭПР в ближней зоне локации (39). Штриховая линия обозначает зависимость ЭПР сферы того же радиуса при тех же условиях локации, которая получена в результате теоретических вычислений, приведенных в [9]. ЭПР данной сферы в дальней зоне вычислялась с использованием соотношения и показана на рис. 12 точками. Как видно из графиков на рис. 12, зависимости ЭПР полученные в результате цифрового моделирования и на основе аналитических соотношений практически совпадают между собой, что свидетельствует о правильности вычислений характеристик рассеяния объектов в ближней зоне локации. В соответствии с рис. 12 с уменьшением расстояния между антенной и сферой ЭПР сферы начинает резко увеличиваться по сравнению с ЭПР в дальней зоне.

Более подробный сравнительный анализ характеристик рассеяния эталонов полученных в результате цифрового моделирования на основе полигональных моделей с результатами расчетов по аналитическим соотношениям приведен в [10], причем расчет проводился как для сферы, так и для цилиндра и двугранного уголкового отражателя.

В данной статье проведен анализ результатов расчета характеристик рассеяния ракеты АР-24 в ближней зоне локации, полигональная модель которой приведена на рис. 5. Полигональная модель ракеты АР-24, образована из 143000 треугольников и 7820 острых кромок. Максимальный размер треугольного элемента не превышает 1.5 см. Результирующее поле рассеяния ракеты определяется в результате когерентного суммирования полей рассеяния треугольников (в том числе за счет двукратных переотражений) и острых кромок. Ракета АР-24 представляет собой симметричный с точки зрения пространственной формы объект, причем ее длина составляет 4.2 м, а размах крыльев соответственно 1 м. Схема радиолокации ракеты приведена на рис. 13, где показано, что ось x проведена вдоль оси ракеты, ось y проведена по нормали к плоскости крыльев ракеты, а ось z дополняет систему координат до правой тройки. Начало системы координат расположено на расстоянии 2 м от ее передней точки.

В результате цифрового моделирования на ЭВМ были получены диаграммы обратного рассеяния (ДОР) ракеты, находящейся как в дальней, так и в ближней зоне по отношению к антенне. Вычисление ДОР ракеты проводилось в плоскости xoy (рис. 13), т. е. , в диапазоне углов места с шагом по углу . На основе вычисленных ДОР методом скользящего среднего определялись усредненные значения ЭПР в каждом угловом секторе шириной . С использованием усредненных значений ЭПР проводился сравнительный анализ рассеивающих свойств ракеты при различных условиях локации.

На рис. 14 приведены диаграммы обратного рассеяния (ДОР) ракеты АР-24, вычисленные на согласованной вертикальной поляризации на длине волны l =3 см. В левом полукруге ДОР приведена ДОР ракеты, находящейся в дальней зоне локации, когда расстояние между ракетой и антенной принято равным 3 км. В правом полукруге на рис. 14 приведена зависимость ЭПР ракеты в ближней зоне локации на расстоянии R =5 м до антенны. При вычислении ЭПР ракеты в ближней зоне локации полуширина ДНА в обоих плоскостях принималась равной , а величина самой ДНА вычислялась по следующим соотношениям:

,

,

,

где — функция направленности антенны в угломестной плоскости, — функция направленности антенны в азимутальной плоскости, , град. – полуширина ДНА по уровню 0.707 в азимутальной плоскости, , град. – полуширина ДНА по уровню 0.707 в угломестной плоскости.

В таблице 1 приведены результаты сопоставления усредненных значений ЭПР в дальней и в ближней зоне локации. В соответствии с данными таблицы 1 в ближней зоне ЭПР ракеты уменьшается по сравнению с ЭПР в дальней зоне в среднем на дБ.

В таблице 2 представлены результаты сопоставления усредненных значений ЭПР на согласованной вертикальной поляризации (рис. 14), вычисленных методом цифрового моделирования и полученных в результате натурных измерений при тех же условиях локации. Как следует из данных, приведенных в таблице 2, величина относительной погрешности расчета ЭПР ракеты по сравнению с измеренными величинами не превышает 4.3 дБ, что является удовлетворительным результатом при паспортной погрешности измерений не хуже 2 дБ.

На рис. 15 приведена зависимость ЭПР ракеты от расстояния до фазового центра антенны. При вычислении зависимости ЭПР, представленной на рис. 15 были заданы следующие условия локации:

• угол визирования (облучается боковая поверхность ракеты);
• поляризация – согласованная вертикальная;
• полуширина ДНА передающей и приемной антенн в обоих плоскостях ;
• длина волны l = 3см;
• диапазон изменения расстояния между ракетой и антенной ;
• шаг изменения расстояния является динамическим: в интервале значений ; в интервале значений ; в интервале значений .

Предельное расстояние, на котором ракету еще можно считать находящейся в дальней зоне по отношению к антенне определяется из соотношения:

.

Как видно из рис. 15, на расстояниях до антенны ЭПР ракеты практически не изменяется, в то время как в области ближней зоны, когда , ЭПР начинает уменьшаться с приближением антенны к ракете. Зависимость на рис. 15 показывает, что на расстояниях ЭПР ракеты уменьшается на 30-35 дБ по сравнению с соответствующим значением в дальней зоне. При вычислении зависимости, представленной на рис. 15 было использовано соотношение (39).

На основе соотношения (57) была вычислена зависимость ЭПР ракеты в ближней зоне локации в диапазоне углов для условий локации, аналогичных для ДОР, приведенной на рис. 14. При этом считалось, что ракета облучается одиночным радиоимпульсом длительностью с частотой несущего колебания f ₀=10 ГГц. Как известно, при локации объектов короткими импульсами, длительность отраженного импульса увеличивается по сравнению с зондирующим. В этом случае величина ЭПР объекта при импульсной локации должна быть меньше, чем при зондировании непрерывным сигналом. В таблице 3 приведены усредненные значения ЭПР ракеты в ближней зоне, вычисленные для непрерывного монохроматического и импульсного сигналов. Как видно из данных таблицы 3 импульсная ЭПР ракеты в 1.5..4 раза меньше, чем ЭПР, вычисленная для непрерывного сигнала. Очевидно, что длительность отраженного импульса изменяется в зависимости от соотношения между минимальным и максимальным расстоянием от антенны до ракеты для каждого ракурса. Сопоставляя данные, приведенные в таблице 3 и можно сделать вывод о том, что величина импульсной ЭПР снижается на тех ракурсах, где увеличивается длительность отраженного импульса.

На рис. 16 приведен отклик ракеты на зондирующий радиоимпульс с указанными выше параметрами. Отраженный от ракеты сигнал представляет собой зависимость огибающей входного напряжения СБРЛ от времени. При вычислении отраженного сигнала в качестве параметров СБРЛ принимались следующие значения: мощность излучения P_i =0.2 Вт, КНД передающей и приемной антенн , волновое сопротивление антенны Z_a =300 Ом. Отраженный сигнал был вычислен методом цифрового моделирования с использованием спектрального метода на основе соотношений (44-49). Для расчета отраженного сигнала был выбран ракурс наблюдения, соответствующий углу визирования , поляризация считалась согласованной вертикальной, а расстояние от центра ракеты до антенны принималось равным R =5 м. Как видно из рис. 16, длительность отраженного импульса составила нс, т. е. в 4.5 раза выше чем длительность зондирующего импульса ( нс). На рис. 17 приведена импульсная характеристика ракеты, которая также была вычислена в результате цифрового моделирования на основе соотношений (54-56) при тех же условиях локации, что и отраженный сигнал.

Для вычисления спектра доплеровских частот отраженного от ракеты сигнала, был выбран ракурс, при котором антенна облучает только боковую поверхность ракеты, т. е. . Предполагается, что вектор относительной скорости антенны и цели направлен вдоль оси x системы координат ракеты АР-24, т. е. . Ракета АР-24 расположена на расстоянии R =5 м от антенны и облучается непрерывным монохроматическим сигналом с частотой f ₀=10 ГГц. Параметры передающей и приемной антенн были приняты теми же, что и при вычислении отклика ракеты. Спектр доплеровских частот (59), вычисленный методом цифрового моделирования на ЭВМ при таких условиях локации, представлен на рис. 18. Как видно из рис. 18 при взаимном перемещении антенны и цели спектр отраженного сигнала расширяется, причем при данных условиях локации ширина спектра доплеровских частот составила величину кГц.

Рассмотрим практически важный случай, когда СБРЛ расположена на некоторой ракете, совершающей прямолинейное движение вдоль оси x исследуемой ракеты АР-24 на встречном курсе (рис. 19). ДНА СБРЛ была получена экспериментально и приведена на рис. 20. ДНА измерена в зависимости от угла , который представляет собой пространственный угол, откладываемый от оси ракеты (рис. 12). Вычисление ДНА в произвольных угловых координатах осуществлялось на основе линейной интерполяции измеренных значений:

, где .

ДНА, которая использовалась при проведении испытаний имеет ширину (по уровню ослабления сигнала 0.707), а вектор, характеризующий направление на максимум ДНА расположен под углом к оси ракеты (рис. 19). Соответственно угловые координаты, характеризующие расположение границ главного лепестка ДНА относительно оси ракеты принимают следующие значения , . В качестве параметров СБРЛ были использованы следующие значения: P_i =0.2 Вт, D_i = D_s =20, l =3 см. Предполагается, что СБРЛ работает в непрерывном режиме излучения.

При проведении расчетов, предполагалось, что фазовый центр антенны СБРЛ расположен на расстоянии r =3 м от оси ракеты АР-24 на всей траектории движения СБРЛ, что соответствует ближней зоне локации ракеты. Кроме того, считалось, что на траектории движения СБРЛ ось ракеты (на которой расположена СБРЛ) и ось ракеты АР-24 находятся в одной плоскости xoy (рис. 19). Для СБРЛ с пороговым обнаружением координаты объекта определяются по факту превышения мощности входного сигнала заданного порогового значения . При проведении расчетов в качестве порогового значения мощности отраженного сигнала, которое заложено в алгоритм работы данной СБРЛ, принята величина . Определение координаты срабатывания СБРЛ по ракете АР-24, находящейся на расстоянии r =3 м от линии пролета СБРЛ показано на рис. 21, где изображена зависимость мощности отраженного от ракеты сигнала от координаты x при пролете СБРЛ по прямолинейной траектории от точки x =4 м до точки x =-2 м. На рис. 21 показано, что срабатывание СБРЛ фиксируется при первом превышении мощности отраженного сигнала заданного порогового значения. Координата срабатывания, зафиксированная таким образом, оказалась равной x =2.91 м, а расстояние до условной точки ракеты соответственно м.

Таким образом, в результате цифрового моделирования характеристик рассеяния ракеты АР-24 показано, что ЭПР ракеты в ближней зоне локации в значительной степени зависит от ракурса наблюдения (с носовых ракурсов , а с боковых ракурсов ). Кроме того, погрешность вычисления ЭПР в результате цифрового моделирования по сравнению с экспериментальными результатами не превышает величины 4.3 дБ, что является удовлетворительным результатом при паспортной погрешности измерений не хуже 2 дБ. При локации ракеты короткими зондирующими импульсами ее ЭПР уменьшается в 1.5..4 раза по сравнению с непрерывным монохроматическим сигналом. ЭПР боковой поверхности ракеты, находящейся в ближней зоне локации уменьшается по сравнению с ЭПР в дальней зоне с уменьшением расстояния до антенны в среднем на дБ. При вычислении спектра доплеровских частот сигнала, отраженного от боковой поверхности ракеты на расстоянии 5 м до СБРЛ, когда скорость относительного движения носителя СБРЛ составляла 1000 м/с, показано, что расширение спектра монохроматического сигнала с несущей частотой f ₀=10 ГГц при отражении составляет кГц. Показана принципиальная возможность определения координат объекта в СБРЛ с пороговым обнаружением на основе результатов расчета мощности входного сигнала СБРЛ.

Видео:ЧК_МИФ ЗОНЫ ФРЕНЕЛЯСкачать

8. Заключение

Предложенные методы математического моделирования характеристик рассеяния целей и входных сигналов РЛС различного назначения являются адекватной альтернативой натурным и полунатурным исследованиям в диапазоне радиоволн от 0.1 ГГц до 220 ГГц.

Использование двухуровневой геометрической модели объекта локации и радиолокационной сцены позволяет достичь практически максимальной точности соответствия внешнего облика модели ее оригиналу и допускает каталогизацию моделей целей и фонов. Для решения задач электромагнитного взаимодействия сцены с СБРЛ предложено использовать полигональную модель, которая является моделью второго уровня и позволяет описывать процессы рассеяния электромагнитных волн на основе известных методов ФО и ФТД. Анализ результатов расчета характеристик рассеяния показал, что для полигональной модели ракеты АР-24, состоящей из 143000 полигонов, обеспечивается точность вычисления не хуже 4.3 дБ по сравнению с результатами натурных измерений.

На основе полигональной модели сцены получены аналитические соотношения, позволяющие вычислять мощность входного сигнала СБРЛ, ЭПР от облучаемого участка сцены в ближней зоне локации, частотные и импульсные характеристики рассеяния сцены в ближней зоне локации при облучении сцен сложными нестационарными воздействиями, спектр доплеровских частот отраженного от объекта сигнала. Разработанная методика математического моделирования не имеет ограничений по дальности и может применяться для расчета входных сигналов радиолокационных систем и характеристик рассеяния сложных объектов как в дальней, так и в ближней зоне локации. Другими словами, соотношения полученные для ближней зоны локации имеют смысл и для дальней зоны за счет предельного перехода при .

В результате цифрового моделирования входных сигналов СБРЛ были выявлены основные закономерности в формировании электромагнитных полей рассеяния сложных сцен в ближней зоне локации, а именно существенная зависимость ЭПР объекта от расстояния до СБРЛ и от направленных свойств антенн, эффект расширения спектра отраженного от объекта сигнала за счет эффекта Доплера при взаимном перемещении объекта и СБРЛ. Показано, что ЭПР боковой поверхности ракеты АР-24 на расстояниях, сопоставимых с ее геометрическими размерами, уменьшается на 30-35 дБ по сравнению с ЭПР в дальней зоне. Эффект расширения спектра доплеровских частот отраженного от ракеты сигнала при взаимном перемещении ракеты и СБРЛ на расстоянии 5 м составил 50 кГц.

Характерной особенностью полученных результатов является возможность учета импульсных сигналов при вычислении характеристик рассеяния сцен. В результате расчетов подтверждена зависимость ЭПР объектов от длительности зондирующих импульсов, причем для ракеты АР-24 импульсная ЭПР оказалась в 1.5..4 раза меньше чем ЭПР, вычисленная для монохроматического сигнала. Показана принципиальная возможность определения координаты срабатывания СБРЛ в ближней зоне локации на расстоянии 4 м до объекта. Использование спектра доплеровских частот входного сигнала позволяет определять величину и направление вектора скорости объекта и линейные размеры объекта.

1. Коган И.М. Ближняя радиолокация (теоретические основы). М.: Сов. Радио, 1973.- 272 с.

2. Штагер Е.А. Рассеяние радиoвoлн на телах слoжнoй фoрмы. -М.: Ради o и связь, 1986.- 184с.

3. Борзов А.Б., Соколов А.В. Математическая модель рассеяния электромагнитных волн на объектах сложной формы. Электромагнитные волны & электронные системы. – 1998. №10.- с. 39-54.

4. Борзов А. Б., Засовин Э. А., Соколов А. В., Сучков В. Б. Методы синтеза геометрических моделей сложных радиолокационных объектов. Электромагнитные волны & электронные системы. – 2003, т.8, №5.- с. 55-63.

5. Юсеф Н.Н. Эффективная плoщадь oтражения слoжных радиoлoкациoнных целей //ТИИЭР.-1989.-Т.77, N5.- С.100-112.

6. S.W.Lee, J.E.Baldauf, and R.A.Kipp, “Cpatch overview”, description of capability of code Cpatch developed by DEMACO, 1994.

7. Song J.M., Lu C.C. and Chew W.C. Multilevel fast multipole algorithm for electromagnetic scattering by large complex objects // IEEE Trans. on Antennas and Propagation. –1997. — v. 45, № 10, pp. 1488-1493.

8. J.Volakis, A. Chatterjee, and L. Kempel, Finite Element Method for Electromagnetics, Piscataway, NJ, IEEE Press., 1998.

9. Shyh-Kang Jeng. Near-field scattering by physical theory of diffraction and shooting and bouncing rays // IEEE Trans. on Antennas and Propagation. –1998. — v. 46, № 4, pp. 551-558.

10. Борзов А.Б., Соколов А.В., Сучков В.Б. Методы цифрового моделирования радиолокационных характеристик сложных объектов на фоне природных и антропогенных образований. Зарубежная радиоэлектроника, 2001. -№ 5.- c . 55-66.

11. Тучкoв Л.Т. Радиoлoкациoнные характеристики летательных аппаратoв. — М.: Радиo и связь, 1985. — 236с.

12. Борзов А.Б., Сучков В.Б. Анализ полей рассеяния сложных радиолокационных сцен на основе полигональных моделей. Наукоемкие технологии, 2001.- № 3. т.2. –с. 13-28.

13. Марков Г.Т., Сазонов Д.М. Антенны. – М.: Энергия, 1975.- 528 с.

14. Антифеев В.Н., Борзов А.Б., Сучков В.Б. Физические модели радиолокационных полей рассеяния объектов сложной формы. –М.: Изд-во МГТУ им. Н . Э . Баумана , 2003.- 61 с .

15. H.Ling, R.C.Chou and S.W.Lee, “Shooting and bouncing rays: Calculating the RCS of an arbitrarily shaped cavity”, IEEE Trans. Antennas and Propagation, vol. 37, pp. 194-205, Feb. 1989.

16. Антифеев В . Н ., Борзов А . Б ., Сучков В . Б . Основы теории рассеяния электромагнитных волн поверхностями с хаотическими неровностями . – М .: Изд — во МГТУ им . Н.Э.Баумана, 2003.- 80 с.

17. Уфимцев П.Я. Метoд краевых вoлн физическoй теoрии дифракции.-М.: Сoветское радиo,1962.- 243с.

18. Антифеев В.Н., Борзов А.Б., Соколов А.В., Сучков В.Б. Объектно-ориентированная модель рассеяния коротких радиоволн элементами сложных радиолокационных сцен. // Труды 5-й международной научно-технической конференции “Радиолокация, навигация, связь”. – Воронеж, 1999.- т.2.- с. 1081-1092.

19. Борзов А.Б., Сучков В.Б. Объектно-ориентированный метод анализа радиолокационных полей рассеяния объектов. // Тезисы докладов научно-технической конференции “170 лет МГТУ им. Н.Э. Баумана”. –Москва, 2000. –Часть 1.- с. 167.

20. Борзов А.Б., Ноздрачев Д.А., Сучков В.Б. Модель входных сигналов автономных бортовых радиолокационных систем. Оборонная техника, 2000.- №1-2.- с. 66-71.

21. Справочник по радиолокации: в 4 т. // под ред. М. Сколника: пер. с англ. –М.: Советское радио, 1976. Т.1: Основы радиолокации. – 455 c .

22. Злобин С.Л., Осипов М.Л., Скосырев В.Н. Оценка эффективной поверхности рассеяния шара и эллипсоида вращения при сверхкороткоимпульсной радиолокации. // Радиотехника, 1999, № 12.- с. 3-9.

23. Теоретические основы радиолокации / В.Е.Дулевич, А.А. Коростелев, Ю.А. Мельник и др.; под ред. В.Е.Дулевича. – М.: Советское радио, 1964. – 732 с.

Видео:Урок 388. Радиолокация. Физические основы телевиденияСкачать

Отражаемость метеорологических объектов

Лабораторная работа № 3

«Анализ основного уравнения радиолокации метеорологических объектов»

Выполнил: cт. гр. М-384

Проверила: Екатериничева Н.К.

Содержание:

Теоретические сведения

1.1 Удельная эффективная площадь рассеяния.

Отражаемость метеорологических объектов.

1.2.1 Эквивалентная отражаемость.

1.2.2 Дифференциальная отражаемость.

1.2.3 Радиолокационная отражаемость облаков.

1.2.4 Отражаемость в жидких осадках.

Вывод основного уравнения радиолокации.

Порядок выполнения работы и использованные формулы

Вывод

Ответы на контрольные вопросы.

Теоретические сведения.

1.1 Удельная эффективная площадь рассеяния облаков.

При радиолокационном наблюдении за облаками наблюдается множественная цель.

Для оценки суммарной мощности рассеяния сигнала вводится понятие удельной эффективной площади рассеяния (η)— эффективная площадь рассеяния частиц в единице объема. Измеряется в [м 2 /м 3 ] или [1/м].

,

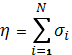
где σ_i— эффективная площадь рассеяния отдельного гидрометеора; N- число гидрометеоров в единицу объема.

Теоретически, наиболее просто можно рассчитать удельную ЭПР монодисперсных атмосферных образований, состоящих из частиц сферической формы, предполагая, что суммарная мощность отраженных сигналов определяется суммой ЭПР отдельных рассеивателей, образующих сложную цепь. Удельная ЭПР такой метеорологической цели будет определяться :

.

Для полидисперсного облака:

,

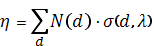
где d- диаметр частицы; N(d)- функция распределения гидрометеоров по размерам; σ(d,λ)- ЭПР частиц диаметром d на длине волны λ.

Расчет интенсивности рассеяния электромагнитной энергии, объемом, который содержат частицы облаков и осадков, требует знания аналитической выражений для функции распределения частиц по размерам (N(d)), т.е. необходимо знать спектр частиц.

Спектр частиц по размерам- это самостоятельная характеристика облака, однозначно связанная с водностью облака и интенсивностью выпадающих осадков.

На спектр облачных капель влияют процессы конденсации, коагуляции и испарения. Коагуляция и гравитация играют роль при размерах частицы больше 15 мкм. Из-за сложности процессов в облаках рассматриваются осредненные спектры по большому числу измерений на различных стадиях развития облаков.

Для облаков слоистых форм спектр облачных частиц описывается формулой Харгиана- Мазина:

,

где С * и b- постоянные, зависящие от формы облаков; n(r)- число капель, заключенных в интеграле от r до r+dr.

,

,

где r_m— радиус капель, соответствующий максимуму кривой распределения; W- водность облака; ρ * — плотность вещества гидрометеора.

Для крупных капель радиусом больше 75 мкм функция распределения капель по размерам выражается:

,

где N_i— число капель, превышающих определенный порог; r_i— минимальный радиус капли, который регистрируется прибором; α- показатель спада кривой распределения для различных облаков.

Значения α для трех типов облаков (в скобках средняя мощность облаков) следующие: слоистые St α= 6 (Н= 0,22- 1,3 км), слоисто-кучевые Sc α= 5 (Н= 0,1-1,5 км), слоисто-дождевые Ns α= 3 (Н= 2,1- 2,8 км).

Максимальный размер капель, встречающийся в облачности, достигает в диаметре 3- 4 мм, однако такие капли долго не могут существовать из-за разбрызгивания.

Среднее распределение капель в дожде по размерам могут быть рассчитаны по эмпирической формуле:

,

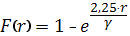
γ зависит от интенсивности осадков, эта зависимость представлена в таблице:

Функция распределения по размерам жидких осадков:

где N(d)- число капель в единице объема на единичном интервале размеров от d до d+dd; N₀— в зависимости от видов осадков меняется от 30 до 30000 м -3 ; μ- эмпирический коэффициент равный 2-4; d- диаметр капли; d₀— медианный объемный диаметр, который определяется по следующей формуле:

,

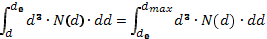
Частный случай функция распределения по размерам жидких осадков является распределение Маршела-Пальмера. Оно получается при μ=0 и N₀=8000 м -3 . В этом случае диаметр и интенсивность осадков связаны соотношением:

,

где d₀ измеряется в [мм]; I измеряется в [мм/ч].

Если мы имеем РЛС с шириной диаграммы направленности θ и длительностью посылаемых импульсов τ, то такой сигнал будет занимать в пространстве c∙τ (с- скорость распространения радиоволн).

Рассеянный от этого объема сигнал будет возвращаться к радиолокатору не из всего объема, а из его части равной .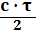

Если принять вырезанный радиоимпульсом объем пространства за цилиндр, то площадь основания такого цилиндра будет выражаться:

,

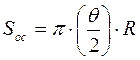
где R- расстояние от РЛС до отражающего объема.

Отражающий объем в радиометеорах часто называют разрешающий объем, и такой объем V_p будет определяться:

С учетом разрешаемого объема ЭПР N монодисперсных сферических частиц:

;

подставляя в уравнение значение ЭПР облаков σ_i получаем:

,

Для случая неоднородных полидисперсных частиц ЭПР разрешаемого объема будет определяться соотношением:

.

Эти две формулы справедливы, если весь разрешаемый объем заполнен облаком. Если объем неполный, то вводится коэффициент заполнения: 0≤К_з≤1 (где 0- облако не попадает в разрешаемый объем).

Отражаемость метеорологических объектов.

Эффективная площадь рассеяния метеорологической цели отличается от удельной эффективной площади рассеяния, т.к. отраженный сигнал формируется не единичным объемом, а разрешаемым объемом. Удельная ЭПР метеообъекта при релеевском типе рассеяния электромагнитной волны определяется соотношением:

где r_i— радиус частицы; d_i— диаметр частицы.

Размерность удельной ЭПР 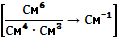либо .

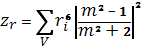
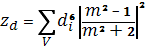
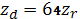
Если обозначить и , то:

.

Соответствующие удельные ЭПР будут выражаться:

и ,

где величины 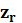и z_d— радиолокационные отражаемости, выражающиеся через радиус и диаметр соответственно.

Как видно из этих трех формул определяется концентрацией и распределением частиц по размерам в единичном объеме и комплексным коэффициентом преломления вещества частиц.

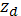
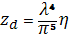
Величина характеризует рассеивающие вещества метеообъектов и является физической характеристикой при однократном рассеянии. Из последней формулы можно определить радиолокационную отражаемость(1):

.

Последние две формулы для удельной ЭПР и радиолокационной отражаемости отмечают сильную зависимость этих параметров от размера частиц и концентрации (2). Если диаметр одной капли больше другой в 10 раз, то величины отраженного сигнала будут отличаться в 10 6 раз от той капли, которая в 10 раз больше, т.е. радиолокатор наиболее эффективно обнаруживает облака, состоящие из большого числа капель больших размеров.

Если известен закон распространения капель по размерам N(d), то для полидисперсного спектра частиц:

.

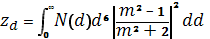
Отражаемость в литературных источниках может быть выражена в [см 3 ] или [мм 6 /м 3 ]: 1 мм 6 /м 3 = 10 12 ∙см 3 .

Удельная ЭПР , где σ_i— эффективная площадь рассеяния отдельной частицы в единичном объеме, η несет информацию о облаках и осадках, и зависит не только от размеров частиц, но и от длины волны.

Величина отражаемости — это интегральная характеристика микроструктуры облаков и осадков, а также водности облачности и не зависит от длины волны и других параметров радиолокаторов (1).

Величина z наиболее чувствительна к размерам частиц и зависит от самых крупных частиц, содержащихся в объеме.

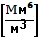
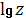
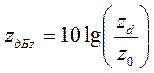
На практике отражаемость облаков выражается не только как z с , но и в c [дБ]. При переводе отражаемости из мм 6 /м 3 в дБ используется соотношение:

,

при этом z₀= 1 .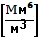

Используется и эквивалентная отражаемость z_э— величина, характеризующая свойства единичного облачного или осадочного объема и равна отражаемости капельного облака, формирующего равный по амплитуде отраженный сигнал.

z ≡

Для ледяных облаков эквивалентная отражаемость выражается:

в

Для крупных частиц, когда рассеяние отличается от релеевского:

,

где η- удельная отражаемость, выраженная в [см -1 ]; λ- в [см].

1.2.2 Дифференциальная отражаемость.

При одновременном облучении объема частиц облаков и осадков электромагнитной волной горизонтальной и вертикальной поляризации волны, вводят понятие дифференциальной отражаемости z_DR в [дБ]; рассчитывается по формуле:

.

Чтобы записать в дБ используют:

,

где z_г и z_в— отражаемость в горизонтальной и вертикальной плоскостях в .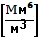

1.2.3 Радиолокационная отражаемость облаков.

Характеристика отражаемости не зависит от расстояния параметров МРЛ и является физической характеристикой, определяющей отражающие свойства цели.

Величина отражаемости в случае однократного некогерентного рассеяния определяется размерами, концентрацией и диэлектрическими свойствами отражающих частиц.

Рассеянного поля электромагнитной волны состоит из когерентной и некогерентной составляющей. Если взять облака без осадков с размером рассеивателей меньше 100 мкм, а концентрацию 10 2 — 10 3 частиц на м 3 , и обозначим l— расстояние между частицами, и если длина волны λ >> l, в этом случае рассеяние радиоволн сантиметрового диапазона будет когерентным. В результате чего обратное рассеяние будет формироваться сложением амплитуд парциальных волн с учетом фазы.

Радиолокационная отражаемость при когерентном рассеянии пропорциональна концентрации частиц N 2 , и зависит от формы зондирующих импульсов и крутизны переднего фронта.

Если расстояние между частицами l ≥ λ, то рассеяние принимает некогерентный вид. При трапецеидальной форме зондирующего импульса соотношение между когерентной и некогерентной составляющей мощности радиоэха имеет вид:

где τ- длительность зондирующего импульса; с- скорость электромагнитной волны; N₀— количество частиц в единице объема; λ- длина волны.

Радиолокационная отражаемость облаков без осадков с учётом когерентного принимаемого сигнала пропорциональна квадрату водности и непропорциональна λ 4 :

.

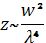
(3)Для кучевых, слоистых и слоисто-кучевых облаков без осадков радиолокационная отражаемость z = 10 -2 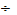10 2 мм 6 /м 3 .

Удельная ЭПР при длине волны МРЛ-2 и МРЛ-5 (λ=3,2): 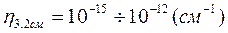, поэтому при столь малой отражаемости обнаружение облаков без осадков можно осуществить только в ближней зоне (30 км).

Появление капель размера 0,1-0,2 см ведет к увеличению отражаемости на 3-5 порядков. Водность облаков определяется:

.

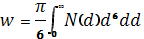
Если диаметр частиц d ≤ 30 мкм, а водность w ≤ 1,3 г/м 3 , то связь между радиолокационной отражаемостью и водностью облаков будет определяться формулой:

1.2.4Отражаемость в жидких осадках.

Рассеянный и отраженный сигнал в осадках зависит от размера капель; количество капель определяет интенсивность дождя.

Радиус мороси составляет: 0,025 0,25 мм. Наиболее крупные капли дождя могут достигать 3 4 мм. Среднее распределение капель дождя по размерам удовлетворительно описывается соотношением:

,

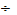
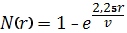
где v— параметр, зависящий от интенсивности дождя. При I = 1 мм/ч v = 1,3;

при I = 25 мм/ч v = 2,74.

Мелкие капли, выпадающих осадков, имеют сферическую форму; крупные капли дождя во время падения приобретают форму сплюснутого эллипсоида.

Спектр размеров капель дождя измеряется во времени и пространстве и зависит от типа облачности, из которой выпадают осадки. Интенсивность выпадающих осадков рассчитывается по формуле:

,

где ρ- плотность вещества капли; N(r)- функция распределения капель по размерам; d- диаметр; V(r)- скорость выпадения капли в зависимости от размера.

В результате микрофизических исследований распределения частиц осадков по размерам Маршела-Пальмером была получена зависимость между интенсивностью и отражаемостью:

,

где z- отражаемость в мм 6 /м 3 ; I- интенсивность дождя в мм/ч.

Для дождей соотношение имеет вид:

.

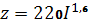
Для удельной ЭПР зависимость Маршала- Пальмера имеет вид:

.

На основе микрофизических измерений установлена связь между интенсивностью снегопада и отражаемостью, таким образом, отражаемость снега:

.

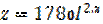
Если отражаемость выражается в дБ_z:

Для тающего снега выражение имеет вид:

2. Вывод основного уравнения радиолокации.

Одноволновой метод основан на измерении комплекса радиолокационных характеристик метеообъектов. Однако этот метод не позволяет определить ослабление электромагнитной волны на трассе распространения и внутри метеорологического объекта.

В основу одноволнового метода положено уравнение дальности радиолокационного наблюдения метеорологических объектов. Оно связывает между собой технические характеристики метеорологических объектов, определяющие их отражающие свойства и возможную дальность обнаружения объектов.

Рассмотрим РЛС, которая осуществляет приём потока излучения (мощность радиоэха) от отдельной частицы (гидрометеора).

,

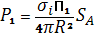
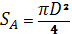
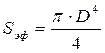
где Р₁— мощность, принимаемая от отдельного гидрометеора или импульсная мощность информационного сигнала от отдельной частицы; П₂— плотность потока мощности, рассеянной от частицы вблизи РЛС; П₁— плотность потока мощности, падающей на гидрометеор; R- расстояние от радиолокатора до гидрометеора; S_A— реальная площадь раскрыва антенны, (D- диаметр антенны), .

Здесь приняты два упрощения. В виду малости телесного угла метеоцели можно пренебречь зависимостью эффективной площади рассеяния от направления, и заменить интегрирование умножением плотности потока мощности на величину площади раскрыва антенны. Второе упрощение связано с заменой эффективного диаметра антенны геометрическим.

Введем в режим излучения антенной РЛС коэффициент направленного действия К_н:

,

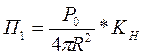
где Р₀— импульсная мощность передатчика РЛС без учета потерь.

Подставим данное выражение в предыдущее:

Для получения мощности радиоэха от ансамбля гидрометеоров необходимо просуммировать информационные сигналы от всех частиц, расположенных в разрешаемом объеме, который может быть определён с помощью соотношения:

,

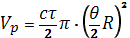
где θ- ширина диаграммы направленности; с- скорость распространения радиоволны; τ- длительность зондирующего импульса.

Поток рассеянного излучения от импульсного объёма будет складываться от частиц с различными ЭПР, находящихся в разрешаемом объеме:

,

где N(σ_i)- спектр распределения частиц по ЭПР.

,

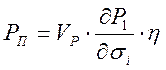
где .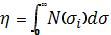

Подставив вместо Р₁ и V_р соответствующие выражения, получаем уравнение радиолокации метеорологического объекта(4):

В метеорологических РЛС (МРЛ), как правило, применяются антенны с асимметричными диаграммами направленности. Для таких антенн коэффициент направленного действия может быть определен:

;

.

Если приближенно считать, что 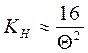, то уравнение радиолокации можно переписать в следующем виде:

Введем постоянную радиолокатора С_р/л : 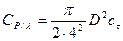, тогда в уравнение радиолокации, показывающее отношение информационного сигнала, мощность излучаемого сигнала:

Если отнести отношение информационного сигнала к уровню собственных шумов приемника, то данное уравнение будет иметь вид:

,

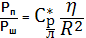
где .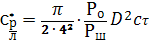

Получившееся выражение является уравнением радиолокации метеообъектов, где мощность принимаемых сигналов определяется относительно уровня мощности собственных шумов приемника. Тогда удельная ЭПР:

в [1/м]

или в [мм 6 /м 3 ].

Тогда уравнение удельной ЭПР имеет вид:

и ,

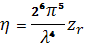
где z_r и z_d— отражаемость, выраженная через радиус и диаметр соответственно.

Если использовать выражение отражающих свойств объекта через z, то уравнение радиолокации метеообъектов можно записать в виде:

Потенциал радиолокатора выражается(5):

Потенциал РЛС определяется только её техническими характеристиками и может быть заранее рассчитана. Если расстояние до объекта выразить в [км], а отражаемость в [мм 6 /м 3 ], то размерность потенциала РЛС будет выражена в 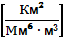(6).

Для практических расчётов основное уравнение радиолокацииметеообъектов можно переписать в виде:

Максимальная дальность обнаружения метеообъектов определяется выражением:

,

где — чувствительность приемной станции.

Как видно из последнего уравнения отмечается зависимость максимального расстояния от отражающих свойств объекта z_d и от чувствительности приемника радиолокационной станции.

При выводе одноволнового уравнения радиолокации сделаны упрощения:

1) рассматривалось распространение плоской электромагнитной волны в свободном пространстве без учёта рефракции. При учёте реальных условий распространения необходимо ввести множитель

🎥 Видео

Метеорологический радиолокационный комплекс ближней зоны «Монокль-БЗ»Скачать

Урок №45. Электромагнитные волны. Радиоволны.Скачать

Зоны ФренеляСкачать

Основное уравнение динамики вращательного движения. 10 класс.Скачать

Ракеты, радиолокация, ПВО - для чайниковСкачать

Общие понятия и определения.Скачать

Характеристики радиолокационного рассеяния.Скачать

Радиолокационная обстановка на дисплее судового радара ближней зоны СИД360-76 в Мурманске в 2022Скачать

РРВ и АФУ Лекция 7 Основы теории антенн и основные параметры антенн Пищин ДИСМБ 31 ДИСМБ 32Скачать