Уравнение работы для адиабатного процесса (5 видео)

Адиабатический процесс и уравнения адиабаты для идеального газа. Пример задачи

Адиабатический переход между двумя состояниями в газах не относится к числу изопроцессов, тем не менее, он играет важную роль не только в различных технологических процессах, но и в природе. В данной статье рассмотрим, что представляет собой этот процесс, а также приведем уравнения адиабаты идеального газа.

Содержание

Кратко об идеальном газе
Что это адиабатический процесс?
Уравнения Пуассона для адиабатического процесса
Пример задачи
2.4. Адиабатный процесс
Адиабатический процесс
Что такое адиабатический процесс
Что такое адиабата
📽️ Видео

Видео:Адиабатный процесс. 10 класс.Скачать

Кратко об идеальном газе

Идеальным называется такой газ, в котором нет взаимодействий между его частицами, и их размеры равны нулю. В природе, конечно же, не существует идеальных на сто процентов газов, поскольку все они состоят из имеющих размеры молекул и атомов, которые взаимодействуют друг с другом всегда как минимум с помощью ван-дер-ваальсовых сил. Тем не менее, описанная модель часто выполняется с достаточной для решения практических задач точностью для многих реальных газов.

Вам будет интересно: Атеизм и антиклерикализм — это. В чем отличие понятий

Главным уравнением идеального газа является закон Клапейрона-Менделеева. Он записывается в следующей форме:

Это уравнение устанавливает прямую пропорциональность между произведением давления P на объем V и количества вещества n на абсолютную температуру T. Величина R — газовая константа, которая играет роль коэффициента пропорциональности.

Видео:Физика 10 класс. Адиабатный процесс.Скачать

Что это адиабатический процесс?

Адиабатический процесс — это такой переход между состояниями газовой системы, при котором обмена энергией с внешней средой не происходит. При этом изменяются все три термодинамических характеристики системы (P, V, T), а количество вещества n остается постоянным.

Различают адиабатическое расширение и сжатие. Оба процесса происходят только за счет внутренней энергии системы. Так, в результате расширения давление и особенно температура системы сильно падают. Наоборот, адиабатическое сжатие приводит к положительному скачку температуры и давления.

Чтобы не происходил обмен теплом между окружающей средой и системой, последняя должна обладать теплоизолированными стенками. Кроме того, сокращение длительности протекания процесса значительно уменьшает тепловой поток от и к системе.

Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Уравнения Пуассона для адиабатического процесса

Первый закон термодинамики записывается в таком виде:

Иными словами, сообщенная системе теплота Q идет на выполнение системой работы A и на повышение ее энергии внутренней ΔU. Чтобы написать уравнение адиабаты, следует положить Q=0, что соответствует определению изучаемого процесса. Получаем:

При изохорном процессе в идеальном газе все тепло идет на повышение внутренней энергии. Этот факт позволяет записать равенство:

Где CV — изохорная теплоемкость. Работа A, в свою очередь, вычисляется так:

Где dV — малое изменение объема.

Помимо уравнения Клапейрона-Менделеева, для идеального газа справедливо следующее равенство:

Где CP — изобарная теплоемкость, которая всегда больше изохорной, так как она учитывает потери газа на расширение.

Анализируя записанные выше равенства и проводя интегрирование по температуре и объему, приходим к следующему уравнению адиабаты:

Здесь γ — это показатель адиабаты. Он равен отношению изобарной теплоемкости к изохорной. Это равенство называется уравнением Пуассона для процесса адиабатического. Применяя закон Клапейрона-Менделеева, можно записать еще два аналогичных выражения, только уже через параметры P-T и P-V:

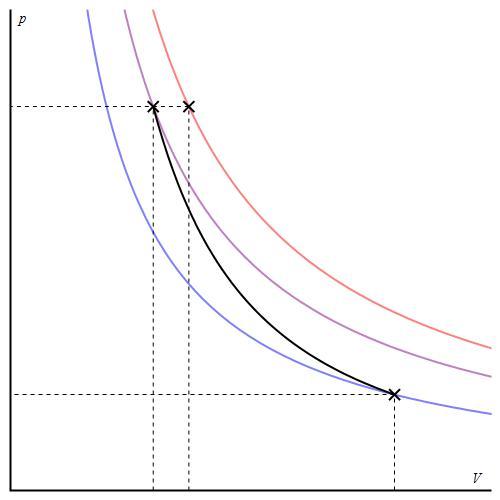
График адиабаты можно привести в различных осях. Ниже он показан в осях P-V.

Цветные линии на графике соответствуют изотермам, черная кривая — это адиабата. Как видно, адиабата ведет себя более резко, чем любая из изотерм. Этот факт просто объяснить: для изотермы давление меняется обратно пропорционально объему, для изобаты же давление изменяется быстрее, поскольку показатель γ>1 для любой газовой системы.

Видео:мкт ИЗОТЕРМИЧЕСКИЙ процесс ИЗОХОРНЫЙ процесс ИЗОБАРНЫЙ процессСкачать

Пример задачи

В природе в горной местности, когда воздушная масса движется вверх по склону, то ее давление падает, она увеличивается в объеме и охлаждается. Этот адиабатический процесс приводит к снижению точки росы и к образованию жидких и твердых осадков.

Предлагается решить следующую задачу: в процессе подъема воздушной массы по склону горы давление упало на 30 % по сравнению с давлением у подножия. Чему стала равна ее температура, если у подножия она составляла 25 oC?

Для решения задачи следует использовать следующее уравнение адиабаты:

Его лучше записать в таком виде:

Если P1 принять за 1 атмосферу, то P2 будет равно 0,7 атмосферы. Для воздуха показатель адиабаты равен 1,4, поскольку его можно считать двухатомным идеальным газом. Значение температуры T1 равно 298,15 К. Подставляя все эти числа в выражение выше, получаем T2 = 269,26 К, что соответствует -3,9 oC.

Видео:Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать

2.4. Адиабатный процесс

Адиабатный процесс — это процесс, при котором не происходит теплообмена с внешней средой.

Физически это означает, что процесс протекает достаточно быстро и система не успевает обменяться теплотой с внешними телами. Однако коль скоро мы имеем дело с равновесными процессами, скорость адиабатного процесса не должна быть слишком уж велика. Примером таких процессов может служить распространение звуковых колебаний в упругой среде.

Выведем уравнение, описывающее адиабатный процесс. Ранее мы имели дело с самыми простыми уравнениями процессов

— для изотермического процесса;

— для изобарного процесса;

— для изохорного процесса.

Поскольку в адиабатном процессе dQ = 0, из первого начала термодинамики следует, что

C другой стороны,

Приравнивая эти выражения, находим

Умножая уравнение (2.28) на V g –1 , получаем в левой части полный дифференциал

В результате интегрирования (2.29) приходим к уравнению адиабатного процесса

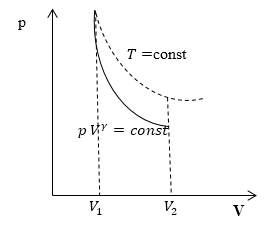
Графически адиабатный процесс описывается на (р,V) — диаграмме кривыми, похожими на изотермы (рис. 2.12), но идущими круче, так как g > 1, поскольку С_p > С_V.

Рис. 2.12. Адиабатный процесс в идеальном газе: 1 — адиабата, 2 — изотерма

Это и понятно, так как при адиабатном расширении газ совершает работу за счет внутренней энергии, и его температура падает, что еще больше уменьшает давление по сравнению с изотермическим расширением.

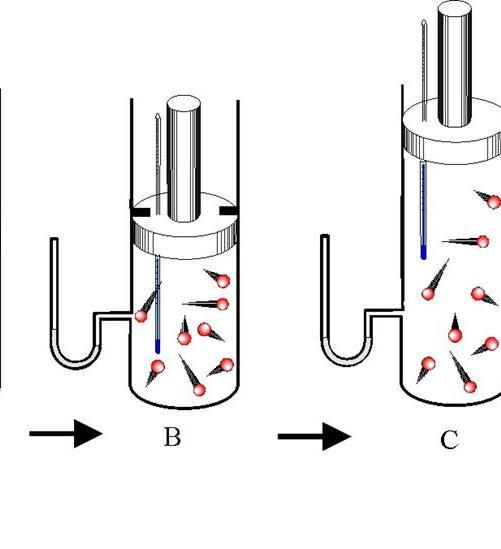
Экспериментальное исследование адиабатного процесса в идеальном газе можно выполнить с помощью установки, представленной на рис. 2.13.

Рис. 2.13. Экспериментальное изучение адиабатного процесса в идеальном газе

Учитывая, что из уравнения состояния идеального газа следует пропорциональность

уравнение адиабатного процесса можно также представить в виде

Первый закон термодинамики в применении к адиабатному процессу позволяет вычислить работу газа при адиабатном расширении:

Выражения для работы при адиабатном процессе с учетом уравнения Клапейрона — Менделеева можно выразить также через температуры в начале и конце процесса

Для бесконечно малых изменений параметров уравнения (2.32), (2.33) переходят в соотношения

Пример. Горючая смесь в двигателе Дизеля (см. рисунок выше) воспламеняется при температуре Т₂ = 1 100 К. Начальная температура смеси Т₁ = 350 К. Определим, во сколько раз нужно уменьшить объем смеси при сжатии, чтобы она воспламенилась. Сжатие будем считать адиабатным. Показатель адиабаты для смеси g = 1,4.

Для решения удобнее воспользоваться уравнением адиабатного процесса в форме (2.31):

Отсюда сразу следует выражение для степени сжатия горючей смеси:

Видео:Физика. Термодинамика: Адиабатный процесс. Центр онлайн-обучения «Фоксфорд»Скачать

Адиабатический процесс

Вы будете перенаправлены на Автор24

Видео:Изопроцессы, Адиабатный процесс.Скачать

Что такое адиабатический процесс

Адиабатическим или адиабатным процессом называют процесс, при котором отсутствует теплообмен с окружающей средой ($delta Q=0$).

В таком случае первое начало термодинамики можно записать в виде:

[0=fracnu RdT+pdV left(1right).]

Из уравнения (1) следует, что при увеличении объема в адиабатном процессе уменьшается температура системы. Или говорят, что в адиабатном процессе работа совершается за счет уменьшения внутренней энергии системы. И обратное справедливо: работа, совершенная над системой, увеличивает внутреннюю энергию системы и, как следствие, температуру. Уравнение, которое характеризует адиабатный процесс в термодинамических параметрах (уравнение адиабаты) носит имя Пуассона. Получим это уравнение для идеального газа. Из уравнения состояния идеального газа:

Из соотношения Майера:

[C_p-C_V=nu R left(3right).]

Подставим (3) в (2), получим:

Разделим уравнение (1) $C_VT ( C_V=fracнR)$, получим:

где $gamma =frac$ — показатель адиабаты. Проинтегрируем уравнение (5):

где $lnA$- некоторая постоянная.

Потенцируем уравнение (6), получаем:

Уравнение (7) есть уравнение адиабаты в параметрах T,V. Для того, чтобы перейти к уравнению адиабаты, в параметрах p,V используют уравнение Менделеева — Клайперона. И получают уравнение адиабаты в виде:

Или в параметрах p,T уравнение (7,8) имеет вид:

Зная, что теплоемкости можно представить как:

показатель адиабаты исходя из ($gamma =frac$) и уравнений (10)

Легко получить формулу работы для адиабатного процесса. По определению работа газа A равна:

где $p_1V_1=nu RT_1.$ Используя уравнение адиабаты, записанное для двух состояний в параметрах $V,T$, получаем:

Видео:29. Адиабатический процесс. Уравнение ПуассонаСкачать

Что такое адиабата

Линия, изображающая на термодинамической диаграмме адиабатный процесс, называется адиабатой (рис.1).

Для сравнения на рис. 1 представлена также изотерма (пунктиром). На рис. 1 видно, что адиабата идет круче, чем изотерма. Работа в адиабатическом процессе по расширению от объема $V_1 $до $V_2$ меньше, чем в изотермическом процессе с таким же изменением объема. Это объясняется тем, что при адиабатном процессе происходит охлаждение газа. В изотермическом процессе при расширении давление уменьшается только за счет уменьшения плотности, тогда как в адиабатном за счет плотности и средней кинетической энергии молекул (соответственно температуры).

Задание: Одноатомный газ совершает адиабатное расширение от объема $V_1=$1$м^3 $при температуре $Т_1=400 К$, при этом давление газа изменяется от $p_1=5cdot ^6Па $до $p_2=2cdot ^6 Па$. Найдите объем газа в конечном состоянии.

При адиабатном расширении имеем:

где $gamma =frac , $так как газ одноатомный, то i=3, следовательно, $gamma =frac=frac$. Значит можно выразить интересующий нас объем:

Ответ: Объем газа в конечном состоянии 4,6 $м^3.$

Задание: Некоторую массу газа сжали так, что $frac=5$, в первом случае процесс проводился адиабатический, второй изотермический. Начальные состояния газов одинаковы в том и другом случае. Найти отношение работ $frac =?$

Работа в адиабатном процессе задана формулой над газом:

Формула для работы в изотермическом процессе имеет вид:

Тогда найдем искомое отношение:

Для коэффициента адиабаты мы знаем формулу вычисления через число степеней свободы$(i)$, а для одноатомного газа $i=3$:

Подставим данные из условий задачи, получим:

Ответ: Отношение работ, которые совершают над газом в процессах сжатия в адиабатном процессе и изотермическом равно 1,89. Работа над газом в адиабатном процессе больше.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26 11 2021