Пучком плоскостей называют — множество всех плоскостей, проходящих через одну и ту же прямую KM (где KM — общая линия (прямая) пересечения плоскостей также называют её осью пучка см. рисунок ниже).
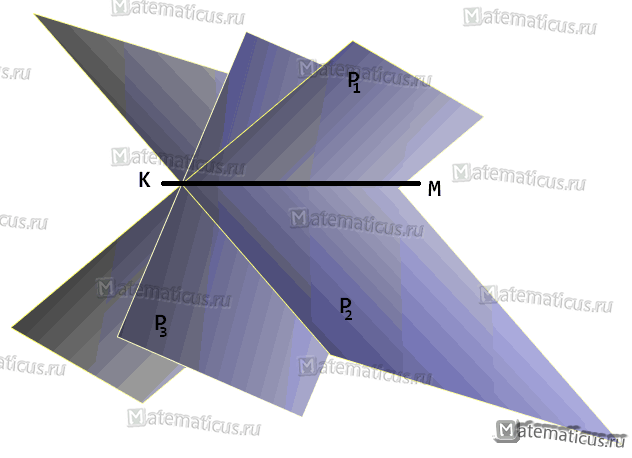
Если известны уравнения двух различных плоскостей P1 и P2
принадлежащих пучку, то каждую плоскость пучка можно представить уравнением вида:
Это уравнение называется уравнением пучка плоскостей
Когда m1≠0, можно разделить уравнение на m1. Обозначив m1:m2 через λ, получим уравнение:
Пример 1
Даны уравнения
5х-3у=0 и 3z-4x=0
Уравнение пучка есть:
m1 ⋅ (5х-3у) + m1 ⋅ (3z-4x )=0
Например, взяв m1=1, m2=-2, будем иметь:
1 ⋅ (5х-3у) + (-2) ⋅ (3z-4x )=0
Отсюда получаем:
13x-3y-6z=0
Уравнение представляет одну из плоскостей пучка.
Пример 2
Найти уравнения проекции прямой T
2x+3y+4z+5=0, x-6y+3z-7=0
на плоскость P
2x+2y+z+15=0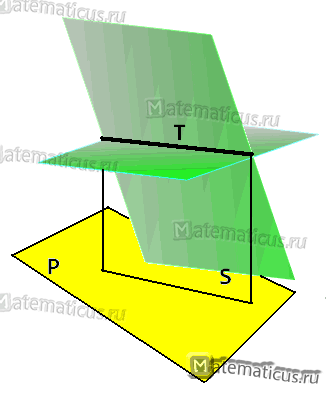 
Решение
Искомая проекция представляется уравнением вида:
(2x+3y+4z+5)+λ ⋅ (x-6y+3z-7)=0
Чтобы найти λ, представим в виде:
(2+λ) ⋅ х+(3-6λ) ⋅ у+(4+3λ) ⋅ z+5-7λ=0 (1)
и запишем условие перпендикулярности плоскостей:
Подставляя A=2, B=2, C=1, получаем:
2 ⋅ (2+λ)+2 ⋅ (3-6λ)+1 ⋅ (4+3λ)=0
Отсюда λ=2. Подставляя λ=2 в уравнение (1), получим уравнение плоскости S. Искомая проекция представляется уравнениями:
Видео:§10 Пучок прямыхСкачать
Пучок прямых. Уравнение пучка прямых
В данной статье мы рассмотрим понятие пучка прямых. Представим уравнение пучка прямых. Приведем примеры нахождения уравнения пучка прямых, проходящих через данную точку.
Пучком прямых называется множество прямых, проходящих через данную точку P. P называется центром пучка прямых . Две разные прямые в пучке прямых определяют центр пучка прямых.
 |
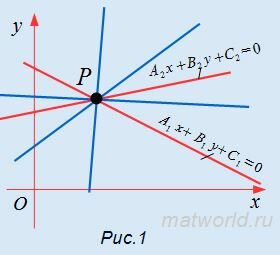Найдем уравнение пучка прямых, центром которого служит точка пересечения двух прямых (Рис.1):
| A1x+B1y+C1=0 | (1) |
| A2x+B2y+C2=0. | (2) |
Докажем следующую теорему.
Теорема 1. Пусть (1) и (2) уравнения двух прямых, пересекающихся в точке P, а λ1 и λ2 некоторые числа, которые одновременно не равны нулю. Тогда
| λ1(A1x+B1y+C1) +λ2(A2x+B2y+C2)=0. | (3) |
является уравнением прямой, проходящей через точку P. Обратно, любая прямая, проходящая через точку P определяется уравнением (3), при некотороых числах λ1 и λ2.
Доказательство. Во первых покажем, что уравнение (3) является линейным уравнением (уравнением первого порядка), т.е. уравнением, при котором коэффициент при x или y не равен нулю.
Группируем коэффициенты при x и y:
| (λ1A1+λ2A2)x+(λ1B1+λ2B2)y+(λ1C1+λ2C2)=0 | (4) |
| λ1A1+λ2A2=0, λ1B1+λ2B2=0. | (5) |
Тогда, например при λ1≠0 (по условию теоремы хотя бы один из чисел λ1 и λ2 не равен нулю), получим:
 | (6) |
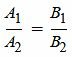 . | (7) |
Полученное равенство является условием параллельности прямых, определяемых уравнениями (1) и (2), что противоречит условию теоремы (эти прямые пересекаются и не совпадают). Таким образом хотя бы один из равенств (5) не выполняется, т.е. хотя бы один коэффициент при x и y в уравнении (4) не равен нулю. Отсюда следует, что уравнение (4) является линейным уравнением (уравнением первой степени) и является уравнением некоторой прямой. По условию теоремы, эта прямая проходит через точку P(x0, y0), которая является пересечением прямых (1) и (2), т.е. выполняются равенства:
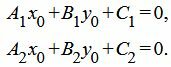 | (8) |
Из уравнениий (8) следует, что при любых λ1 и λ2:
| λ1(A1x0+B1y0+C1)+λ2(A2x0+B2y0+C2)=0, |
т.е. уравнение (3) проходит через точку P.
Докажем вторую часть теоремы. Покажем, что любая прямая, проходящая через точку P определяется уравнением (3) при некоторых значениях λ1 и λ2.
Возьмем некоторую прямую проходящую через точки P и M’(x’, y’). Покажем, что данная прямая определяется уравнением (3) при некоторых значениях λ1 и λ2, не равных одновременно нулю.
В первой части доказательства теоремы мы показали, что прямая, проходящая через точку P определяется уравнением (3). Теперь, если эта прямая проходит через еще одну точку M’(x’, y’), то координаты этой точки должны удовлетворять уравнению (3):
| λ1(A1x’0+B1y’0+C1)+λ2(A2x’0+B2y’0+C2)=0, | (9) |
Заметим, что выражения в скобках не могут быть равным нулю одновременно, т.к. это означало бы, что оба уравнения проходят через точки P и M’(x’, y’) и, следовательно, совпадают. Пусть, например, λ1(A1x’0+B1y’0+C1)≠0. Тогда задав λ2 произвольное число, отличное от нуля, решим (9) относительно λ1:
 |
Пример 1. Пучок прямых задан уравнениями:
Найти уравнение прямой из пучка прямых, проходящий через точку M(−3, 1).
Решение. Уравнение пучка прямых, заданных прямыми (10) и (11) имеет следующий вид:
| λ1(2x+3y−1)+λ2(x−4y+2)=0. | (12) |
Подставим координаты точки M в уравннение (12):
| λ1(2·(−3)+3·1−1)+λ2(−3−4·1+2)=0. | (13) |
| −5(2x+3y−1)+4(x−4y+2)=0. | (14) |
Упростив уравнение (14), получим уравнение из пучка прямых проходящих через точку M(−3, 1):
Пример 2. Построить уравнение пучка прямых с центром M(4,1):
Решение. Возьмем две различные точки, не совпадающие с точкой M: M1(2,1), M2(−1,3). Построим уравнение, проходящие через точки M и M1. Нормальный вектор n1 этой прямой должен быть ортогональным вектору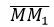 
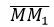
, равному разностьям координат точек M и M1: ==. Т.е. можно взять n1=. Тогда уравнение прямой с нормальным вектором n1, проходяще через точку M имеет следующий вид:
Построим уравнение проходящее через точки M и M2.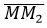 
==. Возмем в качестве нормального вектора второго уравнения n2=. Тогда второе уравнение имеет слеждующий вид:
| 2x+5y−13=0. | (16) |
Из уравнений (15) и (16) можно записать уравнение пучка прямых с центром M(4,1):
| λ1(y−1)+λ2(2x+5y−13)=0. |
| λ1(y−1)+λ2(2x+5y−13)=0. |
Заметим, что взяв другие точки M1 и M2, мы получим уравнение того же пучка прямых, но с другими двумя прямыми.
Видео:112. Уравнение пучка прямых на плоскости.Скачать
Пучок плоскостей
Доказательство необходимого условия. Дано: плоскость π3 принадлежит пучку, образованному плоскостями π1 и π2, следовательно, π1, π2, π3 принадлежат одному пучку плоскостей. Так как плоскости π1 и π2 различны, то ранг матрицы M≤2. Следовательно, левые части уравнения плоскостей π1 и π2 линейно независимы. Поэтому, левая часть в уравнении плоскости π3 может быть представлена как линейная комбинация плоскостей π1 и π2, то есть существуют константы λ и μ, такие, что (1) A3x+B3y+C3z+D3=λ(A1x+B1y+C1z+D1)+μ(A2x+B2y+C2z+D2), где A3=λA1+μA2, B3=λB1+μB2, C3=λC1+μC2, D3=λD1+μD2.
Докажем достаточные условия теоремы 2. Дано: равенство 1, требуется доказать, что π1, π2, π3 принадлежат одному пучку плоскостей. В самом деле, из равенства 1 следует, что A3=λA1+μA2, B3=λB1+μB2, C3=λC1+μC2, D3=λD1+μD2. Тогда третья строка матрицы M есть линейная комбинация первых двух строк этой матрицы. Следовательно, ранг матрицы M≤2, тогда, в силу теоремы 1, плоскость π3 принадлежит пучку плоскостей, образованному π1 и π2. Следствие из теоремы 2: уравнение плоскости, проходящей через прямую пересечения двух плоскостей π1 и π2, заданных своими общими уравнениями относительно ПДСК, имеет вид A1x+B1y+C1z+D1+α(A2x+B2y+C2z+D2)=0, α=μ/λ≠0.
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
💥 Видео
Математика без Ху!ни. Уравнение плоскости.Скачать
Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать
Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать
11. Прямая в пространстве и ее уравненияСкачать
1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать
10. Параллельность и перпендикулярность плоскостей Решение задачСкачать
Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать
Лекция 23. Виды уравнений прямой на плоскости.Скачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать
17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать
Записать уравнение прямой параллельной или перпендикулярной данной.Скачать
Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать
4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать
2. Уравнение плоскости примеры решения задач #1Скачать
3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать
§11 Уравнение прямой, проходящей через две точки на плоскостиСкачать
