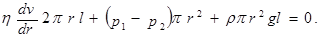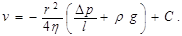Занимаясь исследованием кровообращения, французский врач и физик Пуазейль пришел к необходимости количественного описания процессов течения вязкой жидкости вообще. Установленные им для этого случая закономерности имеют важное значение для понимания сущности гемодинамических явлений и их количественного описания.
Пуазейль установил, что вязкость жидкости может быть определена по объему жидкости, протекающей через капиллярную трубку. Этот метод применим только к случаю ламинарного течения жидкости.
Пусть на концах вертикальной капиллярной трубки длиной l и радиусом R создана постоянная разность давлений Dр. Выделим внутри капилляра столбик жидкости радиусом r и высотой h. На боковую поверхность этого столбика действует сила внутреннего трения:
(17)
| Рис. 6 Схема для вывода формулы Пуазейля. |
Если р1 и р2 – давления на верхнее и нижнее сечения соответственно, то силы давления на эти сечения будут равны:
Сила тяжести равна Fтяж=mgh=rpr 2 gl.
При установившемся движении жидкости, согласно второму закону Ньютона:
Постоянную интегрирования находим из условия, что при r=R скорость v=0 (слои, прилегающие непосредственно к трубе, неподвижны):
Скорость частиц жидкости в зависимости от расстояния от оси равна:
Объем жидкости, протекающий через некоторое сечение трубки в пространстве между цилиндрическими поверхностями радиусами r и r+dr за время t, определяется по формуле dV=2prdrvt или:
Полный объем жидкости, протекающей через сечение капилляра за время t:
(19)
В случае, когда пренебрегаем силой тяжести жидкости (горизонтальный капилляр), объем жидкости, протекающий через сечение капилляра, выражается формулой Пуазейля: 
(20)
Формулу 20 можно преобразовать: разделим обе части этого выражения на время истечения t. Слева получим объемную скорость течения жидкости Q (объем жидкости, протекающий через сечение за единицу времени). Величину 8hl/ 8pR 4 обозначим через Х.. Тогда формула 20 принимает вид:
(21)
В такой записи формула Пуазейля (ее еще называют уравнением Гагена-Пуазейля) аналогична закону Ома для участка электрической цепи.
Можно провести аналогию между законами гидродинамики и законами протекания электрического тока по электрическим цепям. Объемная скорость течения жидкости Q является гидродинамическим аналогом силы электрического тока I. Гидродинамическим аналогом разности потенциалов j1-j2 является перепад давлений Р1 — Р2. Закон Ома I =(j1-j2)/R имеет своим гидродинамическим аналогом формулу 20. Величина Х представляет собой гидравлическое сопротивление — аналог электрического сопротивления R.
Факторы, влияющие на вязкость крови в организме.
Вязкость крови в живом организме зависит, в основном, от скорости сдвига, свойств плазмы, относительного объема эритроцитов и механических свойств эритроцитов, температуры.
Скорость сдвига.
Скоростью сдвига называют величину градиента скорости движения параллельных слоев жидкости ( 
). Вязкость крови зависит от скорости сдвига в диапазоне 0,1-120 с -1 . При скорости сдвига>100 с -1 вязкость достигает значения асимптотической вязкости и при дальнейшем увеличении скорости сдвига (>200 с -1 ) не меняется (рис.10).
 Рис. 10. Зависимость вязкости крови и ньютоновской жидкости от скорости сдвига. |
При низких скоростях сдвига в крови эритроциты выстраиваются в монетные столбики. Это определяет высокую вязкость крови, которая, строго говоря, в этом случае не может рассматриваться как чистая жидкость. По мере увеличения скорости сдвига, агрегаты эритроцитов распадаются, и вязкость крови снижается, приближаясь постепенно к некоторому пределу. При высоких скоростях сдвига, например, в крупных артериях, кровь можно рассматривать как ньютоновскую жидкость. Только в этом случае кровь рассматривается как суспензия форменных элементов и ее свойства можно изучать in vitro на модели суспензии эритроцитов в физиологическом растворе.
Плазма.
Плазма ведёт себя как линейно-вязкая ньютоновская жидкость с относительной вязкостью 1,2. При рассмотрении течения в артериальных сосудах плазма принимается несжимаемой и вязкой с кинематической вязкостью 0,04 см 2 /с.
Неньютоновский характер крови обусловлен наличием форменных элементов крови, в основном, эритроцитов.
Гематокрит.
Одним из основных факторов, определяющих вязкость крови, является объемная концентрация эритроцитов. Отношение суммарного объема эритроцитов к объему крови называют гематокритом. В норме гематокрит равен 0,4-0,5 отн. ед. С повышением гематокрита вязкость крови увеличивается (рис.11).
Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать
Течение вязкой жидкости. Формула Пуазейля
Занимаясь исследованием кровообращения, французский врач и физик Ж. Пуазейль пришел к необходимости количественного описания процессов течения вязкой жидкости вообще. Установленные им для этого случая закономерности имеют важное значение для понимания сущности гемодинамических явлений и их количественного описания.
Не производя строгих математических расчетов, проанализируем, от чего зависит объем V вязкой жидкости, лами- нарно протекающей по участку гладкой трубы длиной L и радиусом г (рис. 9.10). Очевидно, этот объем будет прямо пропорционален времени истечения жидкости t и тому перепаду давлений Рх — Р2, который обусловливает ток жидкости на участке трубы длиной L. Естественно, что объем вытекающей жидкости будет резко возрастать и с увеличением площади поперечного сечения рассматриваемого участка. Теоретические расчеты и непосредственный эксперимент показывают, что V
г 4 . Помехой истечению жидкости является ее вязкость г|, поэтому объем V
1/г. Чем больше длина участка, тем больше потери в скорости протекающей по нему жидкости, значит V
1/L. Приведенные соображения, строгое теоретическое рассмотрение и непосредственный эксперимент приводят к формуле Пу- азейля:
Рис. 9.10. Движение жидкости по участку гладкой трубы
Разделив обе части этого выражения на время истечения t, получим формулу Пуазейля для объемной скорости течения жидкости: 
По аналогии с законом Ома для участка электрической цепи это соотношение можно записать в виде более простой формулы Гагена — Пуазейля:
Величина X, входящая в это уравнение, называется гидравлическим сопротивлением участка трубы или сосуда:
Между законами гидродинамики и законами протекания электрического тока по электрическим цепям существует тесная аналогия. Объемная скорость течения жидкости Q = V/t является гидродинамическим аналогом силы электрического тока I = q/t. Причиной возникновения электрического тока является разность электрических потенциалов (р: — (р2 на соответствующем участке цепи, а причиной движения жидкости — разность давлений Рх — Р2 на участке трубы. В законе Ома I = (cpi — cp2)/i? величина R — электрическое сопротивление проводника, аналогом которого в формуле (9.10) является величина X = 8rL/nr 4 , представляющая собой гидравлическое сопротивление участка трубы или сосуда.
Если от общих законов истечения вязкой жидкости перейти к задачам гемодинамики, то с помощью уравнения Гаге- на — Пуазейля можно определить ряд характеристик кровотока. Так, зная объемную скорость кровотока Q и величину гидравлического сопротивления X сосудов, можно найти величину давления крови в любой точке сосудистой системы:
Если Р0 — давление крови в желудочке сердца, а X — общее сопротивление сосудов на участке сосудистой системы между этим желудочком и некоторой точкой, то давление крови Р в этой точке определяется формулой (9.12).
Гидравлическое сопротивление X разветвленного участка сосудистой системы может быть определено по аналогии с расчетом общего электрического сопротивления участка электрической цепи, состоящего из набора отдельных резисторов. При последовательном соединении сосудов (рис. 9.11, а) общее сопротивление определяется суммой гидравлических сопротивлений их отдельных участков:
Рис. 9.11. Виды ветвления сосудистого русла: а — последовательное; б — параллельное а при параллельном ветвлении сосудистого русла (рис. 9.11, б) общее сопротивление X находится из уравнения
Следует отметить, что аналогия в описании электрических цепей и гидродинамических процессов плодотворно используется при моделировании гемодинамических явлений.
Видео:Формула ПуазёйляСкачать
ПУАЗЁЙЛЯ ЗАКО́Н
В книжной версии
Том 27. Москва, 2015, стр. 727
Скопировать библиографическую ссылку:
ПУАЗЁЙЛЯ ЗАКО́Н (закон Гагена – Пуазёйля), утверждает, что при установившемся ламинарном движении вязкой несжимаемой жидкости сквозь цилиндрич. трубу круглого сечения объёмный расход за 1 с выражается формулой $Q=πR^4(p_0-p_i)/8μl$ , где $l$ – длина трубы, $R$ – её радиус, $p_0$ и $p_i$ – давление жидкости на входе и выходе трубы, μ – коэф. динамич. вязкости. Эта формула, представляющая собой точное решение Навье – Стокса уравнения , экспериментально установлена нем. учёным Г. Гагеном (1839) и независимо Ж. Л. М. Пуазёйлем (1840–41). П. з. справедлив в части трубы, достаточно удалённой от входа и выхода, где достигается ламинарный характер течения. Позднее П. з. был обобщён на течение в плоском канале и в трубе произвольного поперечного сечения.
🎬 Видео
Вязкость и течение Пуазёйля (видео 14) | Жидкости | ФизикаСкачать
Физиология. Гемодинамика. Закон Гагена и Пуазейла.. #40Скачать
Определение коэффициента вязкости жидкости. Проверка закона СтоксаСкачать
Вывод уравнений движения идеальной жидкости - Лекция 2Скачать
Определение коэффициента вязкости жидкости с помощью капиллярного вискозиметраСкачать
Движение тел в жидкостях и газах. Лобовое сопротивление и подъемная сила. Формула Стокса. 10 класс.Скачать
Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать
Режимы течения жидкости, ламинарный и турбулентный режимыСкачать
Потери напора при движении жидкостиСкачать
Урок 19. Относительность движения. Формула сложения скоростей.Скачать
Закон БернуллиСкачать
Физиология кровообращения: физиология давления, артериальное давление, пульс, гемодинамикаСкачать
Уравнение движения с постоянным ускорением | Физика 10 класс #6 | ИнфоурокСкачать
Урок 202. Давление под искривленной поверхностью жидкости. Формула ЛапласаСкачать
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать
Физические основы гемодинамики. Определение вязкости жидкостей с помощью вискозиметра.Скачать
Основы биофизики. Гемодинамика. Часть 1Скачать
Физика. 10 класс. ГидродинамикаСкачать
