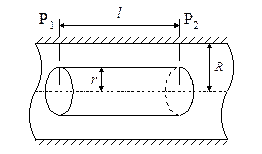
Уравнение пуазейля для ламинарного движения (6 видео)

Ламинарное течение жидкости в трубе. Формула Пуазейля

Рассмотрим стационарный поток жидкости, ламинарно текущей через капилляр круглого сечения (рис. 5)

Рис. 5. К выводу формулы Пуазейля.

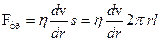
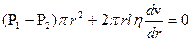
Мысленно выделим в жидкости цилиндр радиуса r и длины l. Обозначим давление на его торцах через Р₁ и Р₂. При ламинарном течении сила давления (Р₁-Р₂)pr 2 уравновешивается силой вязкого трения, действующей на цилиндр со стороны наружных слоев жидкости. Эта сила равна , где s=2prl – поверхность цилиндра, h – вязкость, dv/dr – градиент скорости. Приравнивая к нулю сумму сил, действующих на цилиндр, получим

. (7)

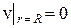
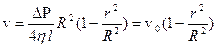
Интегрируя это равенство и учитывая очевидное граничное условие , получим

, (8)

где v₀ = 2v_ср – осевая, численно максимальная скорость течения, v_ср – средняя по расходу скорость жидкости. Таким образом, скорость жидкости квадратично меняется с радиусом и максимальна на оси трубки (см. рис. 2).

Расход жидкости Q, т.е. объем, ежесекундно протекающий через поперечное сечение трубки, равен

. (9)

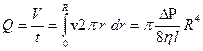
Формула (9) носит название формулы Пуазейля. Она показывает, что вязкость жидкости можно определить, измеряя ее расход Q, перепад давления DP, длину трубки и ее радиус.

Соотношение (9) используется для определения вязкости жидкостей методом Пуазейля. Пропуская жидкость через капилляр известного радиуса, измеряя перепад давления и поток Q, можно найти h.

Формула Пуазейля применима только к ламинарному течению жидкости. Для определения характера течения жидкости вычислим число Рейнольдса из общей формулы (6)

, (10)

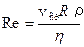
где r – плотность жидкости. Если Re

Дата добавления: 2015-12-16 ; просмотров: 2074 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

ПУАЗЁЙЛЯ ЗАКО́Н

В книжной версии

Том 27. Москва, 2015, стр. 727

Скопировать библиографическую ссылку:

ПУАЗЁЙЛЯ ЗАКО́Н (закон Гагена – Пуазёйля), утверждает, что при установившемся ламинарном движении вязкой несжимаемой жидкости сквозь цилиндрич. трубу круглого сечения объёмный расход за 1 с выражается формулой $Q=πR^4(p_0-p_i)/8μl$ , где $l$ – длина трубы, $R$ – её радиус, $p_0$ и $p_i$ – давление жидкости на входе и выходе трубы, μ – коэф. динамич. вязкости. Эта формула, представляющая собой точное решение Навье – Стокса уравнения , экспериментально установлена нем. учёным Г. Гагеном (1839) и независимо Ж. Л. М. Пуазёйлем (1840–41). П. з. справедлив в части трубы, достаточно удалённой от входа и выхода, где достигается ламинарный характер течения. Позднее П. з. был обобщён на течение в плоском канале и в трубе произвольного поперечного сечения.

Видео:Режимы течения жидкости, ламинарный и турбулентный режимыСкачать

Движение жидкости (газа) в круглой трубе. Формула пуазейля

Рассмотрим ламинарное течение жидкости (газа) в трубе радиусом R (см. рис. П 3). Выделим в этой трубе цилиндр длиной L Меньшего радиуса R. На внешнюю поверхность этого цилиндра будет действовать сила, обусловленная вязкостью:

. (11)

На торцы цилиндра действуют силы F1 и F2, обусловленные давлениями P1 и P2, результирующее воздействие которых на цилиндр равно

Как было отмечено выше, ламинарное течение является стационарным. При стационарном течении движение рассматриваемого нами цилиндра будет осуществляться без ускорения. Тогда на основе второго закона Ньютона с учетом направления действия сил можем записать, что

. (12)

Разделив переменные и произведя интегрирование, получим выражение для скорости движения частиц жидкости (газа) в круглой трубе при ламинарном режиме течения в зависимости от расстояния от оси:

. (13)

Постоянную интегрирования C найдем из условия равенства нулю скорости частиц на стенке трубы (т. е. при R = R). Это условие выполняется при

. (14)

Таким образом, выражение для V можно переписать в виде

. (15)

Из последнего выражения легко определить скорость на оси трубы (R = = 0):

. (16)

. (17)

Таким образом, изменение скорости по сечению трубы получается параболическим.

Найдем расход (поток) жидкости, т. е. объем жидкости, протекающей через поперечное сечение трубы за единицу времени. Разобьем поперечное сечение трубы на кольца шириной Dr (рис. П 2). Через кольцо радиусом R За секунду пройдет объем жидкости, равный произведению площади кольца 2PRdr На скорость течения в точках, находящихся на расстоянии R От оси трубы: