В продолжение предыдущей статьи «Есть ли плазма в космосе?» я хотел бы в познавательных целях рассказать об уравнениях, которые применялись при выводе уравнения Дебая-Хюккеля. Это уравнение Пуассона и распределение Больцмана.
Мы выяснили, что плазма квазинейтральна в равновесном состоянии и что под действием электрического поля от движущихся зарядов, заряженные частицы смещаются на дебаевскую длину и поле в пределах этой длины затухает. В электростатике взаимодействие заряженных частиц описывается кулоновским уравнением:
где – величины взаимодействующих точечных зарядов,
– квадрат расстояния между зарядами. Коэффициент k является константой. Если мы используем систему в электростатических единицах СГС, обозначаемых СГСЭq, то k = 1. Если используется система СИ, то
, где
– диэлектрическая проницаемость среды, в которой расположены заряды,
– электрическая постоянная, равная 8,86 ∙
.
В физике непосредственно силой не пользуются, а вводят понятие электростатического поля распределённых зарядов и измеряют поле величиной напряженности электрического поля. Для этого в каждую точку поля мысленно помещают единичный пробный заряд и измеряют силу, с которой поле зарядов действует на пробный заряд:
Отсюда, если подставить в это уравнение силу Кулона, то получим:
Но и этим физики не ограничиваются, для того чтобы описать полноценно электрическое поле. Рассмотрим единичный заряд, помещённый в электростатическое поле. Поле выполняет работу по перемещению этого заряда на элементарное расстояние ds из точки P1 в точку P2:
Величину называют разностью потенциалов или напряжением. Напряжение измеряется в Вольтах. Знак минус говорит нам о том, что само поле выполняет работу для переноса единицы положительного заряда. Силы, перемещающие заряды являются консервативными, так как работа по замкнутому пути равна всегда нулю, независимо от того, по какому пути перемещается заряд.
Отсюда следует глубокий смысл разности потенциалов. Если зафиксировать точку Р1 и перемещать заряд в переменную точку Р2, то работа зависит только от положения второй точки Р2. Таким образом мы можем ввести понятие потенциала. Потенциал – это силовая функция, показывающая какую необходимо выполнить работу полю, чтобы переместить заряд из бесконечности в данную точку P2, где условно принимают потенциал в бесконечности равным нулю.
Чтобы понять уравнение Пуассона, необходимо разбираться в «особой» векторной математике. Я вкратце расскажу про такие понятия как градиент поля и дивергенции (подразумевается, что читатель знаком с математическим анализом)
Пусть f(x,y,z) является некоторой непрерывной дифференцируемой функцией координат. Зная её частные производные в каждой точке пространства можно построить вектор, компоненты которого x, y, z равны соответствующим частным производным:
где – единичные векторы соответствующих осей x, y, z. Значок
читается «набла» и является дифференциальным оператором
Этот оператор ввёл в математику Гамильтон. С набла можно выполнять обычные математические операции, такие как обычное произведение, скалярное произведение, векторное произведение и так далее.
Теперь вернёмся к электростатическому полю E. С одной стороны изменение потенциала при переходе из одной точки в другую имеет следующий вид:
С другой стороны, согласно формуле (*)
Применяя только что введённое понятие градиент, эта формула преобразуется в:
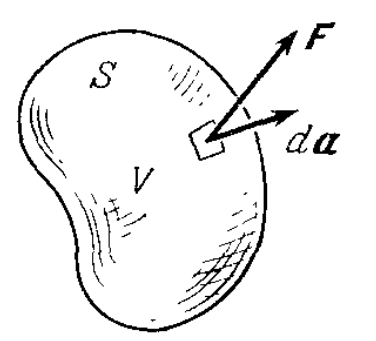
Теперь разберёмся с таким понятием, как дивергенция поля. Рассмотрим конечный замкнутый объем V произвольной формы (см. рис. ниже). Обозначим площадь этой поверхности S. Полный поток вектора F, выходящего из этого объема по определению равно
, где da является бесконечно малым вектором, величина которого равна площади малого элемента поверхности S, а направление совпадает с наружной нормалью к этому элементу.
Возьмём этот поток вектора F поделим на объём и найдём предел при
стремящейся к нулю, т.е. будем стягивать объём в бесконечно малую точку.
Мы подошли к понятию дивергенции. Обозначается дивергенция символом div и является отношением потока вектора F к объёму V, при V стремящейся к нулю.
Прежде чем показать, как получается уравнение Пуассона, важно знать закон Гаусса и теорему Гаусса. Представим себе сферу, внутри которой находится заряд q. Заряд создаёт вокруг себя электрическое поле напряжённости E. Возьмём поток вектора E
где S площадь нашей сферы равная . Следовательно
Это и есть закон Гаусса, утверждающий, что поток электрического поля E через любую замкнутую поверхность равен произведению на полный заряд, охватываемый поверхностью:
где – плотность объёмного заряда, т.е. величина электрического заряда в единице объёма, и
– элементарный объём, выделенный внутри нашего замкнутого объёма.
Теорема Гаусса (полное название теорема Гаусса-Остроградского) чисто математическая теорема о дивергенции. Перепишем полный поток вектора F следующим образом:
В пределе, когда N → ∞, →0 величина в скобках становится дивергенцией и сумма переходит в объёмный интеграл:
Это и есть теорема Гаусса, и является поистине самой важной формулой полевой теории. Применим эту теорему к электростатическому полю. С одной стороны, согласно закону Гаусса
А с другой стороны, согласно теореме Гаусса (только не путайте теорему с законом Гаусса):
Комбинируя два последних уравнения, получим:
Вспомним формулу (**) и подставим сюда вместо E потенциал поля
Дивергенция градиента это новый оператор, который в математике называют оператор Лапласа, или сокращённо лапласиан. Лапласиан обозначается значком набла следующим образом и равен
Перепишем предыдущую формулу в форме лапласиана:
Наконец мы получили уравнение Пуассона. В первой статье это уравнение было немного в другой форме, с учётом диэлектрической проницаемости среды. Вспомните силу Кулона в системе СИ, там константа . Соответственно в законе Гаусса будет не
, а коэффициент
. Таким образом получаем уравнение Пуассона в форме представленной в предыдущей статье
Таким образом по сути уравнение Пуассона – это закон Кулона (а точнее закон Гаусса) переписанный в другой форме, в обозначениях векторного дифференциального анализа.
В следующей статье мы разберём важное распределение из математической статистики — распределение Больцмана.
Видео:Уравнения математической физики. Дельта-функция Дирака. Обобщенные функции.Скачать

Общее решение уравнения Пуассона.
Если система зарядов сосредоточена в ограниченном объёме можно указать общее решение уравнения Пуассона (10.1). В соответствии с принципом суперпозиции скалярный потенциал системы точечных зарядов равен сумме потенциалов, создаваемых полем каждого заряда в отдельности: ϕ(r→) = ∑ j q ∣r→ −r→j∣. (11.1)
Переходя к непрерывному распределению зарядов этот результат можно представить в виде интеграла ϕ(r→) = ∫ V ρ(r′→)dV ′ ∣r→ −r′→∣, (11.2)
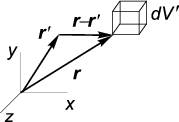
где r→, r′→ — радиусы-векторы точки наблюдения и элементарного объёма dV ′, соответственно (рис. 1.23). Интеграл распространяется на весь объём, где плотность зарядов ρ не равна нулю. Формулу (11.2) называют общим решением уравнения Пуассона. В теории она играет очень важную роль, но в практических вычислениях используется редко. Часто бывает удобнее использовать приближенные формулы, полученные на её основе.
Покажем теперь, как совершить обратный переход и из общего решения уравнения Пауссона (11.2) получить потенциал точечного заряда. Для этого необходимо признать необычные свойства функции плотности заряда ρ(r→): она равна нулю всюду, кроме точки, где расположен заряд, однако, будучи проинтегрированной по объему, даёт конечное значение заряда «точки». Таким свойствами обладает дельта-функция, введённая английским физиком Дираком. Математики относят её к классу обобщенных функций. Для одного заряда q, расположенного в точке r→j, положим ρ(r→) = q δ(r→ −r→j). (11.3)
Трехмерная δ-функция δ(r→ − ρ(r→j) обладает следующими свойствами:
δ(r→ −r→j) всюду, кроме точки r→ = ρ(r→j);
∫ f(r→)δ(r→ −r→j)dV = f(r→j), где f(r→) — любая непрерывная функция; в частности, если f ≡ 1, то ∫ δ(r→ −r→j)dV = 1.
Подставляя (11.3) в общее решение (11.2), получаем
ϕ(r→) = ∫ qδ(r→′ −r→j)dV ′ ∣r→ −r→′∣ = q ∣r→ −r→j∣ .
Следовательно, для системы точечных зарядов из интеграла (11.2) получается сумма (11.1).
Сравнивая потенциал точечного заряда ϕ = q∕r (расположенного в точке r→j = 0) с уравнением для этого потенциала Δϕ = −4π q δ(r→), получаем важное для теории математическое представление δ-функции: Δ1 r = −4πδ(r→) . (11.4)
Рис. 1.24: График функции exp(−x∕a2) πa при последовательно уменьшающихся значениях параметра a: 0,4, 0,2 и 0,1.
С физической точки зрения, распределение заряда в виде δ-функции есть объект предельно малых размеров, которыми можно пренебречь по сравнению с другими размерами задачи. При этом не исключено, что в другой задаче тот же объект нельзя будет считать малым. Существует множество представлений δ-функции, получаемых из гладких функций при предельных переходах. Например:
δ(r→) = lima→0 exp(−r2∕a2) (πa2)3∕2 .
Наряду с трехмерной δ-функцией вводят также δ-функции других размерностей. Например, одномерная δ-функция используется для описания поверхностного распределения заряда: ρ(x) = σ δ(x). (11.5)
Её также можно представить в виде предельного перехода; например:
δ(x→) = lima→0 exp(−x∕a2) πa .
Одномерная δ-функция обладает свойствами, аналогичными свойствам трехмерной δ-функции:
δ(x) = 0 всюду, кроме x = 0;
Однако аналога представления (11.4) для неё не существует. Заметим также, что
Для полноты картины осталось проверить, что интеграл (11.2) действительно удовлетворяет уравнению Пуассона, т.е.
Δ ∫ V ρ(r→′)dV ′ ∣r→ −r→′∣ = −4πρ(r→).
Для этого заметим, что оператор Δ можно внести под знак интеграла, поскольку Δ подразумевает дифференцирование по координатам r→, а интегрирование производится по r→′. Далее воспользуемся соотношением (11.4) и свойствами δ-функции:
Δϕ = ∫ ρ(r→′)Δ 1 ∣r→ −r→′∣ dV ′ = ∫ ρ(r→′)[ − 4π δ(r→ −r→′)]dV ′ = −4πρ(r→).
Видео:9. Уравнение ПуассонаСкачать

Уравнение Пуассона и математическая постановка задач электростатики
Существует большое количество случаев, когда самым удобным методом нахождения напряженности поля считается решение дифференциального уравнения для потенциала. После его получения применим в качестве основы теорему Остроградского-Гаусса в дифференциальной форме:
где ρ является плотностью распределения заряда, ε 0 — электрической постоянной, d i v E → = ∇ → E → = ∂ E x ∂ x + ∂ E y ∂ y + ∂ E z ∂ z — дивергенцией вектора напряженности и выражением, связывающим напряженность поля и потенциал.
Произведем подстановку ( 2 ) в ( 1 ) :
Учитывая, что d i v g r a d φ = ∇ 2 φ = ∂ 2 φ ∂ x 2 + ∂ 2 φ ∂ y 2 + ∂ 2 φ ∂ z 2 , где ∆ = ∇ 2 — это оператор Лапласа, равенство ( 3 ) принимает вид:
Выражение ( 4 ) получило название уравнения Пуассона для вакуума. При отсутствующих зарядах запишется как уравнение Лапласа:
После нахождения потенциала переходим к вычислению напряженности, используя ( 2 ) . Решения уравнения Пуассона должны удовлетворять требованиям:
- значение потенциала как непрерывная функция;
- потенциал должен быть конечной функцией;
- производные потенциала как функции по координатам должны быть конечными.
При наличии сосредоточенных зарядов в объеме V , решение уравнения ( 4 ) будет выражаться для потенциала вида:
Общая задача электростатики сводится к нахождению решения дифференциального уравнения, то есть уравнения Пуассона, удовлетворяющего вышеперечисленным требованиям. Теоретические вычисления известны для небольшого количества частных случаев. Если возможно подобрать функцию φ , удовлетворяющую условиям, то она является единственным решением.
В таких задачах не всегда необходимо задавать заряды или потенциалы во всем пространстве. Для нахождения электрического поля в полости, окруженной проводящей оболочкой, достаточно вычислить поле тел, находящихся внутри нее.
Любое решение уравнения Пуассона ограниченной области может быть определено краевыми условиями, накладывающимися на поведение решения. Границы перехода из одной среды в другую имеют условия, которые должны быть выполнены:
E 2 n — E 1 n = 4 π σ , или ∂ φ 1 ∂ n — ∂ φ 2 ∂ n = 0 .
где σ — это поверхностная полость свободных зарядов, n – единичный вектор нормали к границе раздела, проведенный из среды 1 в 2 , τ — единичный вектор, касательный к границе.
Эти уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной вектора напряженностей электрического поля при переходе через любую заряженную поверхность независимо от ее формы и наличия или отсутствия зарядов вне ее.
Видео:29. Адиабатический процесс. Уравнение ПуассонаСкачать

Уравнение Пуассона в сферических, полярных и цилиндрических координатах
Запись уравнения может быть как при помощи декартовых координат, также и сферических, цилиндрических, полярных.
При наличии сферических r , θ , υ уравнение Пуассона запишется как:
1 r 2 · ∂ ∂ r r 2 ∂ φ ∂ r + 1 r 2 sin θ ∂ θ sin θ · ∂ φ ∂ θ + ∂ 2 φ r 2 sin 2 θ ∂ φ 2 = — 1 ε 0 ρ .
В полярных r , θ :
1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ r 2 ∂ θ 2 = — 1 ε 0 ρ .
В цилиндрических r , υ , z :
1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ ∂ z 2 + ∂ 2 φ r 2 ∂ υ 2 = — 1 ε 0 ρ .
Видео:Дельта функцияСкачать

Примеры решения задач
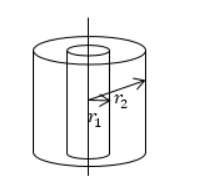
Найти поле между коаксиальными цилиндрами с радиусами r 1 и r 2 и с имеющейся разностью потенциалов ∆ U = φ 1 — φ 2 .
Решение
Необходимо зафиксировать уравнение Лапласа с цилиндрическими координатами, учитывая аксиальную симметрию:
1 r · ∂ ∂ r r ∂ φ ∂ r = 0 .
Решение имеет вид φ = — A ln ( r ) + B . Для этого следует выбрать нулевой потенциал на нужном цилиндре, тогда:
φ ( r 2 ) = 0 = — A ln r 2 + B , следовательно
φ ( r 1 ) = ∆ U = — A ln r 1 + B , получим:
A = ∆ U ln r 2 r 1 .
φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .
Ответ: поле с двумя коаксиальными цилиндрами может быть задано при помощи функции φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .
Найти потенциал поля, которое создает бесконечно круглый цилиндр с радиусом R и объемной плотностью заряда ρ . Использовать уравнение Пуассона.
Решение
Необходимо направить ось Z по оси цилиндра. Видно, что цилиндрическое распределение заряда аксиально симметрично, потенциал имеет такую же симметрию, иначе говоря, считается функцией φ ( r ) с r , являющимся расстоянием от оси цилиндра. Для решения используется цилиндрическая система координат. Уравнение Пуассона в ней запишется как:
φ 2 = C 2 ln r + C ‘ 2 .
C 1 , C ‘ 1 , C 2 , C ‘ 2 — это постоянные интегрирования. Имеем, что потенциал во всех точках должен быть конечным, а l i m r → 0 ln r = ∞ . Отсюда следует, что C 1 = 0 . Далее необходимо пронормировать потенциал, задействовав условие φ 1 ( 0 ) = 0 . Получим C ‘ 1 = 0 .
Поверхностные заряды отсутствуют, поэтому напряженность электрического поля на поверхности шара является непрерывной. Следовательно, что и производная от потенциала также непрерывна при r = R , как и сам потенциал. Исходя из условий, можно найти C 2 , C ‘ 2 :
C 2 ln R + C ‘ 2 = — 1 4 ρ ε 0 R 2 .
C 2 R = — 1 2 ρ ε 0 R .
Значит, полученные выражения записываются как:
Ответ: потенциал поля равняется:
🌟 Видео
Формула ПуассонаСкачать

Формула ПуассонаСкачать

Квантовая механика 44 - Дельта-функция ДиракаСкачать
Дельта функция, Леннаучфильм, 1985Скачать

Уравнения математической физики 11 Формула Пуассона для уравнения теплопроводностиСкачать

Билет №04 "Потенциал электростатического поля"Скачать

Шар заряд.Уравнение ПуассонаСкачать

Останина М.В. - Электродинамика.Лекции.Ч.1 - 3. Векторный и скалярный потенциалы. Уравнение ПуассонаСкачать

Радкевич Е.В. - Уравнения математической физики - 5.Функция Грина задачи Дирихле для ур. ПуассонаСкачать

Уравнение ПуассонаСкачать
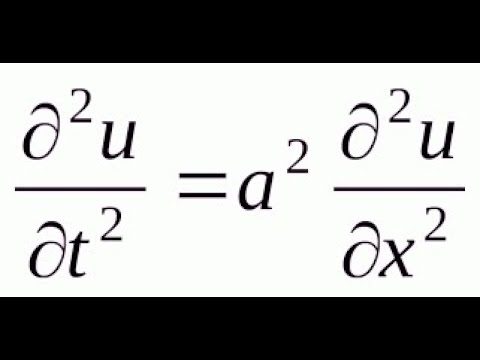
Эквипотенциальные поверхности. Уравнения Пуассона и Лапласа.Скачать

7.2 Задача 1. Краевая задача для уравнения ПуассонаСкачать

Колыбасова В.В. - Методы математической физики.Семинары - 27. Дельта-функцияСкачать

Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Решение Пуассона одномерного уравнения теплопроводностиСкачать

ЧК МИФ 3 1 3 3 5 L4 Уравнение ПуассонаСкачать