Уравнение пуассона решение для потенциалов (6 видео)

Уравнение Пуассона и математическая постановка задач электростатики

Существует большое количество случаев, когда самым удобным методом нахождения напряженности поля считается решение дифференциального уравнения для потенциала. После его получения применим в качестве основы теорему Остроградского-Гаусса в дифференциальной форме:

где ρ является плотностью распределения заряда, ε 0 — электрической постоянной, d i v E → = ∇ → E → = ∂ E x ∂ x + ∂ E y ∂ y + ∂ E z ∂ z — дивергенцией вектора напряженности и выражением, связывающим напряженность поля и потенциал.

Произведем подстановку ( 2 ) в ( 1 ) :

Учитывая, что d i v g r a d φ = ∇ 2 φ = ∂ 2 φ ∂ x 2 + ∂ 2 φ ∂ y 2 + ∂ 2 φ ∂ z 2 , где ∆ = ∇ 2 — это оператор Лапласа, равенство ( 3 ) принимает вид:

Выражение ( 4 ) получило название уравнения Пуассона для вакуума. При отсутствующих зарядах запишется как уравнение Лапласа:

После нахождения потенциала переходим к вычислению напряженности, используя ( 2 ) . Решения уравнения Пуассона должны удовлетворять требованиям:

значение потенциала как непрерывная функция;
потенциал должен быть конечной функцией;
производные потенциала как функции по координатам должны быть конечными.

При наличии сосредоточенных зарядов в объеме V , решение уравнения ( 4 ) будет выражаться для потенциала вида:

Общая задача электростатики сводится к нахождению решения дифференциального уравнения, то есть уравнения Пуассона, удовлетворяющего вышеперечисленным требованиям. Теоретические вычисления известны для небольшого количества частных случаев. Если возможно подобрать функцию φ , удовлетворяющую условиям, то она является единственным решением.

В таких задачах не всегда необходимо задавать заряды или потенциалы во всем пространстве. Для нахождения электрического поля в полости, окруженной проводящей оболочкой, достаточно вычислить поле тел, находящихся внутри нее.

Любое решение уравнения Пуассона ограниченной области может быть определено краевыми условиями, накладывающимися на поведение решения. Границы перехода из одной среды в другую имеют условия, которые должны быть выполнены:

E 2 n — E 1 n = 4 π σ , или ∂ φ 1 ∂ n — ∂ φ 2 ∂ n = 0 .

где σ — это поверхностная полость свободных зарядов, n – единичный вектор нормали к границе раздела, проведенный из среды 1 в 2 , τ — единичный вектор, касательный к границе.

Эти уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной вектора напряженностей электрического поля при переходе через любую заряженную поверхность независимо от ее формы и наличия или отсутствия зарядов вне ее.

Содержание

Уравнение Пуассона в сферических, полярных и цилиндрических координатах
Примеры решения задач
Уравнение Пуассона и математическая постановка задач электростатики
Решение уравнения Пуассона
Готовые работы на аналогичную тему
Уравнение Пуассона в сферических, полярных и цилиндрических координатах
Уравнение Пуассона и Лапласа
Пример 1
Решение
Пример 2
Решение
🎬 Видео

Видео:Билет №04 "Потенциал электростатического поля"Скачать

Уравнение Пуассона в сферических, полярных и цилиндрических координатах

Запись уравнения может быть как при помощи декартовых координат, также и сферических, цилиндрических, полярных.

При наличии сферических r , θ , υ уравнение Пуассона запишется как:

1 r 2 · ∂ ∂ r r 2 ∂ φ ∂ r + 1 r 2 sin θ ∂ θ sin θ · ∂ φ ∂ θ + ∂ 2 φ r 2 sin 2 θ ∂ φ 2 = — 1 ε 0 ρ .

В полярных r , θ :

1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ r 2 ∂ θ 2 = — 1 ε 0 ρ .

В цилиндрических r , υ , z :

1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ ∂ z 2 + ∂ 2 φ r 2 ∂ υ 2 = — 1 ε 0 ρ .

Видео:9. Уравнение ПуассонаСкачать

Примеры решения задач

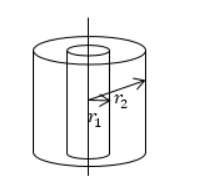
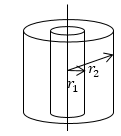
Найти поле между коаксиальными цилиндрами с радиусами r 1 и r 2 и с имеющейся разностью потенциалов ∆ U = φ 1 — φ 2 .

Решение

Необходимо зафиксировать уравнение Лапласа с цилиндрическими координатами, учитывая аксиальную симметрию:

1 r · ∂ ∂ r r ∂ φ ∂ r = 0 .

Решение имеет вид φ = — A ln ( r ) + B . Для этого следует выбрать нулевой потенциал на нужном цилиндре, тогда:

φ ( r 2 ) = 0 = — A ln r 2 + B , следовательно

φ ( r 1 ) = ∆ U = — A ln r 1 + B , получим:

A = ∆ U ln r 2 r 1 .

φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .

Ответ: поле с двумя коаксиальными цилиндрами может быть задано при помощи функции φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .

Найти потенциал поля, которое создает бесконечно круглый цилиндр с радиусом R и объемной плотностью заряда ρ . Использовать уравнение Пуассона.

Решение

Необходимо направить ось Z по оси цилиндра. Видно, что цилиндрическое распределение заряда аксиально симметрично, потенциал имеет такую же симметрию, иначе говоря, считается функцией φ ( r ) с r , являющимся расстоянием от оси цилиндра. Для решения используется цилиндрическая система координат. Уравнение Пуассона в ней запишется как:

φ 2 = C 2 ln r + C ‘ 2 .

C 1 , C ‘ 1 , C 2 , C ‘ 2 — это постоянные интегрирования. Имеем, что потенциал во всех точках должен быть конечным, а l i m r → 0 ln r = ∞ . Отсюда следует, что C 1 = 0 . Далее необходимо пронормировать потенциал, задействовав условие φ 1 ( 0 ) = 0 . Получим C ‘ 1 = 0 .

Поверхностные заряды отсутствуют, поэтому напряженность электрического поля на поверхности шара является непрерывной. Следовательно, что и производная от потенциала также непрерывна при r = R , как и сам потенциал. Исходя из условий, можно найти C 2 , C ‘ 2 :

C 2 ln R + C ‘ 2 = — 1 4 ρ ε 0 R 2 .

C 2 R = — 1 2 ρ ε 0 R .

Значит, полученные выражения записываются как:

Ответ: потенциал поля равняется:

Видео:ЧК_МИФ 3_1_2_4 (L=3- ЛЭТИ) УРАВНЕНИЕ ПУАССОНА ДЛЯ СКАЛЯРНОГО ПОТЕНЦИАЛАСкачать

Уравнение Пуассона и математическая постановка задач электростатики

Вы будете перенаправлены на Автор24

Видео:29. Адиабатический процесс. Уравнение ПуассонаСкачать

Решение уравнения Пуассона

В достаточно большом количестве случаев наиболее удобным методом поиска напряженности поля является решение дифференциального уравнения для потенциала. Получим его, используя в качестве основы теорему Остроградского — Гаусса в дифференциальной форме:

где $rho $ — плотность распределения заряда, $_0$ — электрическая постоянная, $divoverrightarrow=overrightarrowoverrightarrow=frac+frac+frac$) — дивергенция вектора напряженности и выражение связывающее напряженность поля и потенциал:

Подставим (2) в (1), получим:

Учитываем, что $divgradvarphi =^2varphi =frac<^2varphi >+frac<^2varphi >+frac<^2varphi >$, где $triangle =^2$- оператор Лапласа, тогда равенство (3) запишем как:

Уравнение (4) называется уравнением Пуассона (для вакуума) в системе СИ. Если заряды отсутствуют, то уравнение (4) преобразуется в уравнение Лапласа:

После того, как найден потенциал из уравнения Пуассона, обычно вычисляется напряженность по формуле (2). Решения уравнения Пуассона должны удовлетворять таким требованиям:

Потенциал должен быть непрерывной функцией.
Потенциал должен быть конечной функцией.
Производные от потенциала как функции по координатам должны быть конечными.

Если заряды сосредоточены в объеме V, то решением уравнения (4) будет выражение для потенциала вида:

Итак, общая задача электростатики сводится к нахождению решения дифференциального уравнения (уравнения Пуассона), которое удовлетворяет выше перечисленным требованиям. Нахождение решения — задача весьма сложная. Теоретические решения известны для небольшого количества частных случаев. Если удалось подобрать функцию $varphi $, которая удовлетворяет всем условиям задачи, то она единственная.

Готовые работы на аналогичную тему

Не всегда есть необходимости задавать заряды или потенциалы во всем пространстве. Например, если необходимо найти электрическое поле в полости, которая окружена проводящей оболочкой, то можно найти поле только для тел внутри самой полости.

Каждое решение уравнения Пуассона в ограниченной области однозначно определяется краевыми условиями, которые накладывают на поведение решения. На границе перехода из одной среды в другую выполняются граничные условия:

где $sigma $- поверхностная плотность свободных зарядов, n- единичный вектор нормали к границе раздела, проведенный из среды 1 в 2, $tau — $единичный вектор, касательный к границе.

Данные уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной составляющей вектора напряженностей электрического поля при переходе через любую заряженную поверхность не зависимо от формы этой поверхности и наличия и отсутствия зарядов вне ее.

Видео:Останина М.В. - Электродинамика.Лекции.Ч.1 - 3. Векторный и скалярный потенциалы. Уравнение ПуассонаСкачать

Уравнение Пуассона в сферических, полярных и цилиндрических координатах

Уравнение Пуассона может быть записано не только в декартовых координатах, но также в сферических и цилиндрических, полярных.

В сферических координатах ($r,theta ,vartheta)$ уравнение Пуассона имеет следующий вид:

В полярных координатах ($r,theta )$ система координат уравнение имеет вид:

В цилиндрических координатах ($r,vartheta,z)$ уравнение имеет вид:

Задание: Найдите поле между двумя коаксиальными цилиндрами с радиусами $r_1$ и $r_2$, разность потенциалов между которыми равна $triangle U=_1-_2.$

Запишем уравнение Лапласа в цилиндрических координатах с учетом аксиальной симметрии:

Оно имеет решение $varphi =-Aln(r)$+B. Выберем нулевой потенциал на наружном цилиндре, найдем, получим:

$varphi left(r_2right)=0=-Alnr_2+B,$ следовательно

Ответ: Поле между двумя коаксиальными цилиндрами задается функцией $varphi (r)=-frac<<ln left(fracright) >>lnleft(rright)+frac<<ln left(fracright) >>lnr_2$

Задание: Найти, используя уравнение Пуассона потенциал поля, которое создает бесконечно длинный круглый цилиндр радиуса R с объемной плотностью заряда $rho $.

Ось Z направим по оси цилиндра. Так как цилиндрическое распределение заряда аксиально симметрично, то потенциал обладает той же симметрией, то есть он является функцией $varphi left(rright), $где r — расстояние от оси цилиндра. Поэтому используем цилиндрическую систему координат. Запишем уравнение Пуассона в ней с учетом симметрии:

где $C_1$,$ _1,C_2$,$ _2$ — постоянные интегрирования. Так как потенциал во всех точках должен быть конечным, а $<mathop_ lnr >=infty $, следовательно, $C_1=0.$ Пронормируем потенциал условием:$_1left(0right)=0$, тогда: $_1=0.$

Так как поверхностных зарядов нет, то напряженность электрического поля на поверхности шара непрерывна, то есть непрерывна производная от потенциала при r=R. И непрерывен сам потенциал. Эти условия дают два алгебраических уравнения для того, чтобы найти постоянные $C_2$,$ _2:$

Следовательно, получаем выражения для потенциалов:

[_1left(rright)=-fracfrac<_0> r ^ 2 left(0 Ответ: Потенциал поля равен: $$ varphi_1 left(r right)=-fracfrac r^2 left (0

Видео:ЧК_МИФ_3_2_4_2_(L3)_УРАВНЕНИЕ ПУАССОНА ДЛЯ ВЕКТОРНОГО ПОТЕНЦИАЛАСкачать

Уравнение Пуассона и Лапласа

В случае потенциального поля напряженность поля Е может быть выражена через градиент потенциала. При этом приходим к выражению

содержащему двойную дифференциальную операцию: дивергенцию от градиента. При использовании декартовой системы координат легко записать эту операцию через соответствующие производные. Действительно, представляя в формулу (1) составляющие grad φ как:

Операция div grad носит название лапласиана и обозначается знаком Δ. Используя оператор набла, рассматриваемую операцию можно представить как наблу квадрат, таким образом:

В случае декартовых координат и в применении к скалярной функции можно всегда считать операции ∇ 2 и Δ тождественными.

Уравнение (1) является основным уравнением потенциального электрического поля и носит название уравнения Пуассона.

В области поля, где заряды отсутствуют (где ρ = 0), уравнение (1) упрощается, так как в его правой части оказывается нуль. В последнем случае уравнение называют уравнением Лапласа.