Уравнение пуассона для свободных носителей в полупроводнике (2 видео)

Уравнение Пуассона для ОПЗ

Запишем уравнение Пуассона для полупроводника p-типа:

(3.6)

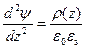
Величина ρ(z) в общем случае, когда отсутствует ограничение на малость возмущения, будет:

. (3.7)

В квазинейтральном объеме, где условие электронейтральности выполняется, ρ(z) = 0.

. (3.8)

Поскольку, как было показано в (3.3 – 3.5),

. (3.9)

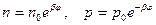
Подставляя (3.9) в (3.6), имеем для нахождения ψ(z) дифференциальное уравнение:

. (3.10)

Домножим выражение для дебаевской длины экранирования, которое представлено в разделе 2.5 формулой (2.23), слева и справа на величину . Тогда

. (3.11)

. (3.12)

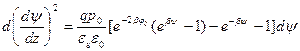
Проинтегрировав (3.12) от бесконечности до некоторой точки ОПЗ, получаем:

. (3.13)

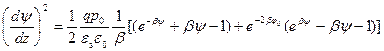
Воспользовавшись определением дебаевской длины экранирования L_D (2.23), а также соотношением , получаем:

. (3.14)

. (3.15)

Из (3.14) и (3.15) имеем:

. (3.16)

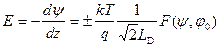
Соотношение (3.16) называется первым интегралом уравнения Пуассона.

Знак электрического поля выбирается в зависимости от знака поверхностного потенциала. Если ψ_s > 0 (обеднение основными носителями или инверсия), поле направлено вглубь полупроводника по оси z и положительно. При ψ_s

Содержание

Уравнение Пуассона и распределение Больцмана (часть 1)
Глава 3. Физика поверхности и МДП-структуры (стр. 2 )
3.2. Заряд в области пространственного заряда
3.2.1. Уравнение Пуассона для ОПЗ
3.2.3. Избыток свободных носителей заряда
🌟 Видео

Видео:9. Уравнение ПуассонаСкачать

Уравнение Пуассона и распределение Больцмана (часть 1)

В продолжение предыдущей статьи «Есть ли плазма в космосе?» я хотел бы в познавательных целях рассказать об уравнениях, которые применялись при выводе уравнения Дебая-Хюккеля. Это уравнение Пуассона и распределение Больцмана.

Мы выяснили, что плазма квазинейтральна в равновесном состоянии и что под действием электрического поля от движущихся зарядов, заряженные частицы смещаются на дебаевскую длину и поле в пределах этой длины затухает. В электростатике взаимодействие заряженных частиц описывается кулоновским уравнением:

где – величины взаимодействующих точечных зарядов, – квадрат расстояния между зарядами. Коэффициент k является константой. Если мы используем систему в электростатических единицах СГС, обозначаемых СГСЭq, то k = 1. Если используется система СИ, то , где – диэлектрическая проницаемость среды, в которой расположены заряды, – электрическая постоянная, равная 8,86 ∙ .

В физике непосредственно силой не пользуются, а вводят понятие электростатического поля распределённых зарядов и измеряют поле величиной напряженности электрического поля. Для этого в каждую точку поля мысленно помещают единичный пробный заряд и измеряют силу, с которой поле зарядов действует на пробный заряд:

Отсюда, если подставить в это уравнение силу Кулона, то получим:

Но и этим физики не ограничиваются, для того чтобы описать полноценно электрическое поле. Рассмотрим единичный заряд, помещённый в электростатическое поле. Поле выполняет работу по перемещению этого заряда на элементарное расстояние ds из точки P1 в точку P2:

Величину называют разностью потенциалов или напряжением. Напряжение измеряется в Вольтах. Знак минус говорит нам о том, что само поле выполняет работу для переноса единицы положительного заряда. Силы, перемещающие заряды являются консервативными, так как работа по замкнутому пути равна всегда нулю, независимо от того, по какому пути перемещается заряд.

Отсюда следует глубокий смысл разности потенциалов. Если зафиксировать точку Р1 и перемещать заряд в переменную точку Р2, то работа зависит только от положения второй точки Р2. Таким образом мы можем ввести понятие потенциала. Потенциал – это силовая функция, показывающая какую необходимо выполнить работу полю, чтобы переместить заряд из бесконечности в данную точку P2, где условно принимают потенциал в бесконечности равным нулю.

Чтобы понять уравнение Пуассона, необходимо разбираться в «особой» векторной математике. Я вкратце расскажу про такие понятия как градиент поля и дивергенции (подразумевается, что читатель знаком с математическим анализом)
Пусть f(x,y,z) является некоторой непрерывной дифференцируемой функцией координат. Зная её частные производные в каждой точке пространства можно построить вектор, компоненты которого x, y, z равны соответствующим частным производным:

где – единичные векторы соответствующих осей x, y, z. Значок читается «набла» и является дифференциальным оператором

Этот оператор ввёл в математику Гамильтон. С набла можно выполнять обычные математические операции, такие как обычное произведение, скалярное произведение, векторное произведение и так далее.

Теперь вернёмся к электростатическому полю E. С одной стороны изменение потенциала при переходе из одной точки в другую имеет следующий вид:

С другой стороны, согласно формуле (*)

Применяя только что введённое понятие градиент, эта формула преобразуется в:

Теперь разберёмся с таким понятием, как дивергенция поля. Рассмотрим конечный замкнутый объем V произвольной формы (см. рис. ниже). Обозначим площадь этой поверхности S. Полный поток вектора F, выходящего из этого объема по определению равно

, где da является бесконечно малым вектором, величина которого равна площади малого элемента поверхности S, а направление совпадает с наружной нормалью к этому элементу.
Возьмём этот поток вектора F поделим на объём и найдём предел при стремящейся к нулю, т.е. будем стягивать объём в бесконечно малую точку.

Мы подошли к понятию дивергенции. Обозначается дивергенция символом div и является отношением потока вектора F к объёму V, при V стремящейся к нулю.

Прежде чем показать, как получается уравнение Пуассона, важно знать закон Гаусса и теорему Гаусса. Представим себе сферу, внутри которой находится заряд q. Заряд создаёт вокруг себя электрическое поле напряжённости E. Возьмём поток вектора E

где S площадь нашей сферы равная . Следовательно

Это и есть закон Гаусса, утверждающий, что поток электрического поля E через любую замкнутую поверхность равен произведению на полный заряд, охватываемый поверхностью:

где – плотность объёмного заряда, т.е. величина электрического заряда в единице объёма, и – элементарный объём, выделенный внутри нашего замкнутого объёма.

Теорема Гаусса (полное название теорема Гаусса-Остроградского) чисто математическая теорема о дивергенции. Перепишем полный поток вектора F следующим образом:

В пределе, когда N → ∞, →0 величина в скобках становится дивергенцией и сумма переходит в объёмный интеграл:

Это и есть теорема Гаусса, и является поистине самой важной формулой полевой теории. Применим эту теорему к электростатическому полю. С одной стороны, согласно закону Гаусса

А с другой стороны, согласно теореме Гаусса (только не путайте теорему с законом Гаусса):

Комбинируя два последних уравнения, получим:

Вспомним формулу (**) и подставим сюда вместо E потенциал поля

Дивергенция градиента это новый оператор, который в математике называют оператор Лапласа, или сокращённо лапласиан. Лапласиан обозначается значком набла следующим образом и равен

Перепишем предыдущую формулу в форме лапласиана:

Наконец мы получили уравнение Пуассона. В первой статье это уравнение было немного в другой форме, с учётом диэлектрической проницаемости среды. Вспомните силу Кулона в системе СИ, там константа . Соответственно в законе Гаусса будет не , а коэффициент . Таким образом получаем уравнение Пуассона в форме представленной в предыдущей статье

Таким образом по сути уравнение Пуассона – это закон Кулона (а точнее закон Гаусса) переписанный в другой форме, в обозначениях векторного дифференциального анализа.

В следующей статье мы разберём важное распределение из математической статистики — распределение Больцмана.

Видео:29. Адиабатический процесс. Уравнение ПуассонаСкачать

Глава 3. Физика поверхности и МДП-структуры (стр. 2 )

Уравнение пуассона для свободных носителей в полупроводнике

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12

Та область в ОПЗ, где суммарная концентрация свободных носителей электронов и дырок меньше, чем концентрация ионизованной примеси, называется областью обеднения. Область в ОПЗ, где концентрация свободных неосновных носителей больше, чем основных, получила название инверсионного канала.

Видео:Формула ПуассонаСкачать

3.2. Заряд в области пространственного заряда

Одной из основных задач при анализе области пространственного заряда полупроводника является нахождение связи между электростатическим потенциалом ψ(z), с одной стороны, и величинами заряда в области пространственного заряда Qs, избытка электронов и дырок Γp, n, емкости ОПЗ Cs – с другой. Нахождение этой связи основано на решении уравнения Пуассона для ОПЗ [2, 14, 21, 13, 11].

3.2.1. Уравнение Пуассона для ОПЗ

Запишем уравнение Пуассона для полупроводника p-типа:

(3.6)

Величина ρ(z) в общем случае, когда отсутствует ограничение на малость возмущения, будет:

. (3.7)

В квазинейтральном объеме, где условие электронейтральности выполняется, ρ(z) = 0.

. (3.8)

Поскольку, как было показано в (3.3 – 3.5),

. (3.9)

Подставляя (3.9) в (3.6), имеем для нахождения ψ(z) дифференциальное уравнение:

. (3.10)

. (3.11)

. (3.12)

Проинтегрировав (3.12) от бесконечности до некоторой точки ОПЗ, получаем:

. (3.13)

Воспользовавшись определением дебаевской длины экранирования LD (2.23), а также соотношением , получаем:

. (3.14)

. (3.15)

Из (3.14) и (3.15) имеем:

. (3.16)

Соотношение (3.16) называется первым интегралом уравнения Пуассона.

Знак электрического поля выбирается в зависимости от знака поверхностного потенциала. Если ψs > 0 (обеднение основными носителями или инверсия), поле направлено вглубь полупроводника по оси z и положительно. При ψs ψs > 0). Заряд в ОПЗ Qsc обусловлен только зарядом ионизованных акцепторов QB. Из (3.16, 3.18) следует, что

. (3.20)

Ширина обедненной области

Область слабой инверсии (2φ0 > ψs > φ0). Заряд в ОПЗ Qsc, так же как и в случае обеднения, обусловлен только зарядом ионизованных акцепторов QB, поскольку заряд свободных электронов Qn 2φ0). Заряд в ОПЗ Qsc обусловлен в основном зарядом свободных электронов вблизи поверхности в инверсионном канале Qn, хотя в начале области сильной инверсии еще существен вклад заряда ионизованных акцепторов

. (3.22)

Величина заряда ионизованных акцепторов QB в ОПЗ и ширина слоя обеднения W не зависят от поверхностного потенциала ys и равны:

. (3.23)

Отметим, что, как следует из рисунка 3.2 и выражений (3.19 – 3.22), область обогащения по многим параметрам подобна области сильной инверсии, а область обеднения – области слабой инверсии. На рисунке 3.3 приведено значение заряда в ОПЗ Qsc как функции поверхностного потенциала ys, рассчитанное для конкретного случая.

Рис. 3.3. Зависимость заряда в ОПЗ от поверхностного потенциала ys, рассчитанная для кремния p‑типа

3.2.3. Избыток свободных носителей заряда

Важной характеристикой ОПЗ является значение заряда свободных носителей (электронов или дырок) Qp, n или, если выразить этот заряд в единицах элементарного заряда, величина избытка электронов или дырок Gp, n в ОПЗ. Определим величину Gp как

, (3.24)

где p(z) – концентрация дырок в ОПЗ, p0 – концентрация дырок в квазинейтральном объеме.

Таким образом, избыток электронов или дырок – это избыточное по сравнению с равновесным в нейтральном объеме число свободных носителей на единицу площади ОПЗ. В ряде источников иногда избыток свободных носителей Gp, n называют поверхностной концентрацией. Это не совсем верно, ибо поверхностная концентрация по своему смыслу есть число свободных носителей заряда на единицу объема, рассчитанное на поверхности полупроводника. А избыток Gp, n есть избыточное число свободных носителей, проинтегрированное по глубине ОПЗ и рассчитанное на единицу площади.

Из (3.24) следует, что

. (3.25)

Аналогично избыток электронов Gn равен:

. (3.26)

Понятиями избытка Gp, n чаще пользуются, когда говорят о свободных носителях в инверсионном канале. Для случая обогащения выражения (3.25, 3.26), рассчитанные с учетом (3.15), при значениях будут иметь вид:

, (3.27)

. (3.28)

Для области слабой и сильной инверсии выражение для Gp, n можно получить в аналитическом виде из выражений для зарядов в ОПЗ, не прибегая к интегрированию (3.25, 3.26).

Действительно, заряд свободных носителей, например, электронов, в инверсионном канале Qn равен разности полного заряда Qsc и заряда ионизованных доноров QB, для которых имеются аналитические выражения:

. (3.29)