Уравнение пуассона для магнитного поля судна (5 видео)

Содержание

Технические средства судовождения. Магнитные компасы (стр. 3 )
2 Магнитное поле судна
2.1. Виды судового железа
2.2 Анализ уравнений Пуассона
Уравнение Пуассона и распределение Больцмана (часть 1)
Уравнение Пуассона для вектора-потенциала
Уравнение Пуассона для вектора-потенциала
💥 Видео

Видео:Магнитное поле ЗемлиСкачать

Технические средства судовождения. Магнитные компасы (стр. 3 )

Уравнение пуассона для магнитного поля судна

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12

Вращающий момент картушки. Магнитная стрелка (картушка) компаса в магнитном поле H Земли подвержена влиянию вращающего (направляющего) момента (рис. 1.2):

L = Fl sin α. (1.10)

где F — сила, действующая на каждый полюс стрелки (F=mH);

l—расстояние между полюсами стрелки;

α — угол отклонения стрелки от вектора H

Выражение L = Fl sin α принимает вид

L = mHl sin α = H sin α

С учетом того, что ml/ μo = M; μoН=В, получаем

L = BM sin α. (1.11)

Работы по усовершенствованию конструкции магнитных компасов не прекращаются. В последние десятилетия XX века сконструированы дистанционные магнитные компасы, к которым можно подключать репитеры, систему автоматического регулирования курса судна и другие устройства штурманского оборудования.

Все магнитные компасы классифицируются по следующим признакам:

1) по принципу действия чувствительного элемента;

2) по наличию дистанционной передачи;

3) по наличию гироскопической стабилизации показаний компаса.

По принципу действия чувствительного элемента магнитные компасы подразделяются на следующие виды:

а) магнитные стрелочные;

Видео:Индукция магнитного поля | Физика 9 класс #37 | ИнфоурокСкачать

2 Магнитное поле судна

Видео:Билет №04 "Потенциал электростатического поля"Скачать

2.1. Виды судового железа

Судовое железо в магнитном отношении можно разделить на две категории — мягкое и твердое. Мягкое железо в поле Земли приобретает индуктивный (временный) магнетизм. При изменении курса судна элементы из мягкого материала перемагничиваются, а при отсутствии внешнего (намагничивающего) поля теряют свой магнетизм. Твердое железо имеет постоянную намагниченность, которая возникает в процессе постройки судна под влиянием сильных намагничивающих полей. Постоянный магнетизм в дальнейшем, при плавании судна, не зависит от курса судна и стабильно сохраняется в течение длительного времени.

Полный вектор индукции земного поля можно представить в виде трех составляющих: X (продольной), Y (поперечной), Z (вертикальной). Продольная X и поперечная Y составляющие при геометрическом сложении образуют горизонтальную составляющую Н. Вектор индукции H определяет направление магнитного меридиана, от которого отсчитывается магнитный курс k судна. Составляющие X и Yможно представить в виде

X = Hcos к; Y = Hsin к. (2.1)

На рис. 2.1 представлен корпус судна в магнитном поле Земли. Поле X намагничивает все продольные элементы судна. Суммарная продольная намагниченность судна характеризуется магнитным моментом МХ = n1Х, пропорциональным индукции намагничивающего поля X. Аналогично поперечное поле Y создает поперечную намагниченность — магнитный момент My=n2Y, а поле Z — вертикальный магнитный момент Mz=n3Z. В этих выражениях n1, n2 и n3 — коэффициенты пропорциональности, зависящие от размеров и формы элементов судна, а также от магнитной восприимчивости мягкого судового железа.

Помимо трех векторов Мх, Му и Mz, характеризующих индуктивное намагничивание, можно также представить вектор Мп— магнитный момент, характеризующий постоянный магнетизм твердого судового железа. Направление вектора Мп в общем случае не совпадает ни с одной из осей (х, у, z). Вектор Мп не зависит ни от курса судна, ни от магнитной широты.

Магнитный компас находится в некоторой точке О. В этой точке магнитное поле создается как бы большими магнитами, имеющими магнитные моменты Мх, Му, Мz, Мп. В точке О есть также магнитное поле Земли, характеризуемое тремя векторами индукции: X, Y,Z.

Коэффициенты пропорциональности а0, d0, go зависят от того, где установлен компас: чем более он удален от судового железа, тем меньше значения этих коэффициентов. Суммируя составляющие векторы индукции в точке О по трем направлениям, получаем уравнения Пуассона:

X’ =X + aX + bY+cZ + P;

Y’ =Y + dX+eY + fZ + Q; (2.2)

Z’ = Z+gX + hY +kZ + R.

Коэффициенты пропорциональности а, b, c, d, e, f, g, h, k называются параметрами Пуассона. Их значения зависят от магнитной восприимчивости мягкого судового железа, размеров и формы элементов корпуса судна, а также от расположения точки О по отношению к судовому железу, т. е. от места установки компаса на судне.

Силы от мягкого железа судна, входящие в уравнение (2.2), могут быть представлены происходящими от прямолинейных брусков мягкого железа.

Силы aX, dX и gX получились от продольного намагничивания мягкого железа судна, силы bY, eY и hY – от поперечного и силы cZ, fZ и kZ – от вертикального.

Таким образом, эти силы можно представить происходящими от продольных, поперечных и вертикальных прямолинейных брусков мягкого железа (рис. 2.1).

Эти бруски, согласно гипотезе Пуассона, будет намагничиваться пропорционально магнитящей силе, т. е. пропорционально одной из составляющих сил X, Y и Z земного магнетизма, вследствие чего приобретут полярность, и каждый из них пошлет на стрелку компаса силу, пропорциональную своему намагничиванию.

Рис. 2.1 Магнитное поле судна

Полагая, что концы брусков удалены от компасной стрелки настолько, что размерами стрелки можно пренебречь, рассматриваем действие данного бруска только на один северный полюс стрелки, предполагая его помещенным в центре компаса. Действие на стрелку обоих концов брусков рассматриваем только в том случае, когда концы бруска находятся на равных расстояниях от центра компаса. В противном случае будем рассматривать действие только ближайшего к стрелке конца бруска, предполагая другой конец удаленным настолько, что он не оказывает влияния на стрелку компаса.

Видео:Асимптотика магнитного поляСкачать

2.2 Анализ уравнений Пуассона

Для того, чтобы судить о величинах сил рассмотрим более подробно их происхождение. На рис. 2.2 показано расположение брусков мягкого железа, образующих силы aX, dX и gX – от продольного намагничивания этих брусков составляющей силой X земного магнетизма, которую для простоты изложения приняли положительной, т. е. направленной к носу судна (линия X показывает общее направление намагниченности всех брусков). В каждом из рассматриваемых случаев один брусок произведет те же силы, что и два или несколько брусков, но эти силы будут меньшие по абсолютной величине.

Рис. 2.2 Расположение брусков мягкого железа, образующих силы от продольного намагничивания

Расположение брусков в первых двух случаях, указанных на рис. 2.2, образует отрицательный параметр a. На судне подобным железом является обшивка судна, стрингеры, киль, продольные переборки и т. п.

Расположению брусков, образующих положительный параметр a, соответствуют на судне горизонтальные стрелы или оси штурвалов.

Магнитное поле судна в точке О характеризуется продольным вектором индукции — аХ. Знак «минус» означает, что вектор силы аХ направлен к корме. Вектор индукции намагничивающего поля +Х имеет знак «плюс», т. к. он направлен от кормы к носу судна. Анализируя выражение отрицательной силы — аХ при положительном значении +Х, приходим к выводу, что параметр а в данной ситуации должен иметь знак «минус». Поскольку на рис. 2.1 представлена типичная схема расположения магнитного компаса на судне, можно сделать вывод: судовой параметр а всегда отрицательный (-а). Величина параметра а, так же как и других параметров Пуассона, зависит от места установки компаса, его удаленности от железных масс судна. Некоторые параметры Пуассона (а, с, е, k) имеют величину на уровне нескольких десятых или сотых долей единицы. Их можно считать множителями 1-го или 2-го порядка малости. Другие параметры (b, d, f, g, h) являются множителями 3-го порядка малости, т. к. их величины исчисляются тысячными долями. В некоторых случаях параметрами 3-го порядка малости можно пренебречь. Имеется мнемоническая схема для запоминания тех параметров и сил в уравнениях Пуассона, которые могут быть исключены ввиду их незначительности.

Судового железа, образующего параметр d у компасов, расположенных в ДП судна, мало; поэтому для этих компасов параметр d близок к нулю, а для главных компасов он может быть принят равным нулю.

Брускам, образующим параметр g, соответствуют на судне продольные крепления надстроек.

Аналогичным путем можно рассмотреть (рис. 2.3) расположение брусков мягкого железа, образующих силы bY, eY и hY от поперечного намагничивания этих брусков составляющей силой Y земного магнетизма, которую для простоты приняли положительной, т. е. направленной к правому борту судна (линия Y показывает общее направление намагниченности всех брусков).

Рис. 2.3 Расположение брусков мягкого железа, образующих силы от поперечного намагничивания

Судового железа, образующего параметры b и h у компасов, расположенных в ДП судна, мало; поэтому для этих компасов указанные параметры близки к нулю, а для главных компасов их можно принимать равным нулю.

Брускам, образующим отрицательный параметр e, соответствуют на судне бимсы и поперечные переборки.

Так же рассмотрим (рис. 2.4) расположение брусков мягкого железа, образующих силы cZ, fZ и kZ от вертикального намагничивания этих брусков составляющей силой Z земного магнетизма, которую приняли положительной, т. е. направленной к килю судна (линия Z показывает общее направление намагниченности всех брусков).

Видео:Физика 9 класс (Урок№19 - Индукция магнитного поля.)Скачать

Уравнение Пуассона и распределение Больцмана (часть 1)

В продолжение предыдущей статьи «Есть ли плазма в космосе?» я хотел бы в познавательных целях рассказать об уравнениях, которые применялись при выводе уравнения Дебая-Хюккеля. Это уравнение Пуассона и распределение Больцмана.

Мы выяснили, что плазма квазинейтральна в равновесном состоянии и что под действием электрического поля от движущихся зарядов, заряженные частицы смещаются на дебаевскую длину и поле в пределах этой длины затухает. В электростатике взаимодействие заряженных частиц описывается кулоновским уравнением:

где – величины взаимодействующих точечных зарядов, – квадрат расстояния между зарядами. Коэффициент k является константой. Если мы используем систему в электростатических единицах СГС, обозначаемых СГСЭq, то k = 1. Если используется система СИ, то , где – диэлектрическая проницаемость среды, в которой расположены заряды, – электрическая постоянная, равная 8,86 ∙ .

В физике непосредственно силой не пользуются, а вводят понятие электростатического поля распределённых зарядов и измеряют поле величиной напряженности электрического поля. Для этого в каждую точку поля мысленно помещают единичный пробный заряд и измеряют силу, с которой поле зарядов действует на пробный заряд:

Отсюда, если подставить в это уравнение силу Кулона, то получим:

Но и этим физики не ограничиваются, для того чтобы описать полноценно электрическое поле. Рассмотрим единичный заряд, помещённый в электростатическое поле. Поле выполняет работу по перемещению этого заряда на элементарное расстояние ds из точки P1 в точку P2:

Величину называют разностью потенциалов или напряжением. Напряжение измеряется в Вольтах. Знак минус говорит нам о том, что само поле выполняет работу для переноса единицы положительного заряда. Силы, перемещающие заряды являются консервативными, так как работа по замкнутому пути равна всегда нулю, независимо от того, по какому пути перемещается заряд.

Отсюда следует глубокий смысл разности потенциалов. Если зафиксировать точку Р1 и перемещать заряд в переменную точку Р2, то работа зависит только от положения второй точки Р2. Таким образом мы можем ввести понятие потенциала. Потенциал – это силовая функция, показывающая какую необходимо выполнить работу полю, чтобы переместить заряд из бесконечности в данную точку P2, где условно принимают потенциал в бесконечности равным нулю.

Чтобы понять уравнение Пуассона, необходимо разбираться в «особой» векторной математике. Я вкратце расскажу про такие понятия как градиент поля и дивергенции (подразумевается, что читатель знаком с математическим анализом)
Пусть f(x,y,z) является некоторой непрерывной дифференцируемой функцией координат. Зная её частные производные в каждой точке пространства можно построить вектор, компоненты которого x, y, z равны соответствующим частным производным:

где – единичные векторы соответствующих осей x, y, z. Значок читается «набла» и является дифференциальным оператором

Этот оператор ввёл в математику Гамильтон. С набла можно выполнять обычные математические операции, такие как обычное произведение, скалярное произведение, векторное произведение и так далее.

Теперь вернёмся к электростатическому полю E. С одной стороны изменение потенциала при переходе из одной точки в другую имеет следующий вид:

С другой стороны, согласно формуле (*)

Применяя только что введённое понятие градиент, эта формула преобразуется в:

Теперь разберёмся с таким понятием, как дивергенция поля. Рассмотрим конечный замкнутый объем V произвольной формы (см. рис. ниже). Обозначим площадь этой поверхности S. Полный поток вектора F, выходящего из этого объема по определению равно

, где da является бесконечно малым вектором, величина которого равна площади малого элемента поверхности S, а направление совпадает с наружной нормалью к этому элементу.
Возьмём этот поток вектора F поделим на объём и найдём предел при стремящейся к нулю, т.е. будем стягивать объём в бесконечно малую точку.

Мы подошли к понятию дивергенции. Обозначается дивергенция символом div и является отношением потока вектора F к объёму V, при V стремящейся к нулю.

Прежде чем показать, как получается уравнение Пуассона, важно знать закон Гаусса и теорему Гаусса. Представим себе сферу, внутри которой находится заряд q. Заряд создаёт вокруг себя электрическое поле напряжённости E. Возьмём поток вектора E

где S площадь нашей сферы равная . Следовательно

Это и есть закон Гаусса, утверждающий, что поток электрического поля E через любую замкнутую поверхность равен произведению на полный заряд, охватываемый поверхностью:

где – плотность объёмного заряда, т.е. величина электрического заряда в единице объёма, и – элементарный объём, выделенный внутри нашего замкнутого объёма.

Теорема Гаусса (полное название теорема Гаусса-Остроградского) чисто математическая теорема о дивергенции. Перепишем полный поток вектора F следующим образом:

В пределе, когда N → ∞, →0 величина в скобках становится дивергенцией и сумма переходит в объёмный интеграл:

Это и есть теорема Гаусса, и является поистине самой важной формулой полевой теории. Применим эту теорему к электростатическому полю. С одной стороны, согласно закону Гаусса

А с другой стороны, согласно теореме Гаусса (только не путайте теорему с законом Гаусса):

Комбинируя два последних уравнения, получим:

Вспомним формулу (**) и подставим сюда вместо E потенциал поля

Дивергенция градиента это новый оператор, который в математике называют оператор Лапласа, или сокращённо лапласиан. Лапласиан обозначается значком набла следующим образом и равен

Перепишем предыдущую формулу в форме лапласиана:

Наконец мы получили уравнение Пуассона. В первой статье это уравнение было немного в другой форме, с учётом диэлектрической проницаемости среды. Вспомните силу Кулона в системе СИ, там константа . Соответственно в законе Гаусса будет не , а коэффициент . Таким образом получаем уравнение Пуассона в форме представленной в предыдущей статье

Таким образом по сути уравнение Пуассона – это закон Кулона (а точнее закон Гаусса) переписанный в другой форме, в обозначениях векторного дифференциального анализа.

В следующей статье мы разберём важное распределение из математической статистики — распределение Больцмана.

Видео:Физика - Магнитное полеСкачать

Уравнение Пуассона для вектора-потенциала

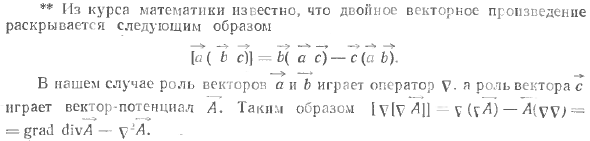
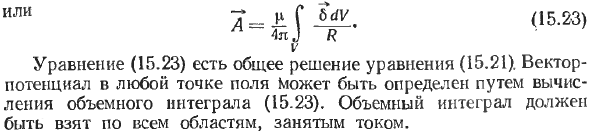
Видео:МАГНИТНОЕ ПОЛЕ за 24 минуты. ЕГЭ Физика. Николай Ньютон. ТехноскулСкачать

Уравнение Пуассона для вектора-потенциала

Уравнение Пуассона векторного потенциала. Умножим проницаемость среды p с обеих сторон (15.4): P rot II = pd. Согласитесь обрабатывать носители, которые можно подразделить на отдельные области, чтобы проницаемость p каждой области была постоянной.

Если p является константой, ее можно разместить под знаком p ротора. // ‘= rot B = p (15.17) (15.17) использует rot A вместо B. ротрот A = pb. (15.18) Операция по извлечению ротора из ротора в основном представляет собой

операцию по открытию двойного векторного произведения Людмила Фирмаль

и выполняется следующим образом **: rot rot A = [V [VA] 1 = grad div A -V2 A = p 6 (15.19) ** Из курса математики известно, что произведение двойного вектора раскрывается как [a (bc)] — b (ac) -c (ab ). В этом случае роли векторов a и b играет оператор V.

Роль вектора c играет векторный потенциал A. Следовательно, IVIV ^ 11-V (? A) -A (== grad divZ-v ‘L. 4 — это вычисляемая функция, поэтому вы имеете право подчиняться требованиям поля DC divH-O (15.20)

Не было никаких дополнительных требований к потенциальному вектору, что означает, что линия вектора A является линией, замкнутой сама по себе с учетом (15.20). Уравнение (15.19)

Следующая форма rd (15.21) (15.21) — не что иное, как уравнение Пуассона, в отличие от уравнения (13.26): оно построено относительно векторных величин, а -> — ■ «-> — * + / -J-

уравнение (13.26) построено относительно скалярных величин Людмила Фирмаль

Заменить на kA2 и заменить плотность тока q на + + v27 ^ — | -. Последнее уравнение для скалярных величин Al и A Разделенный на три составленных уравнения: *, Ar: P2L = -rbg (15.22a) (15.226) (15.22c) (15.22a) to t, (15.226) to /, (15.22c) К к

Если их добавить, их общие решения аналогичны уравнениям (13.26), уравнение (15.23) является общим решением уравнения (15.21), а векторный потенциал в любой точке поля

Может быть определен путем вычисления интеграла объема (15.23), который должен быть получен по всей площади, занимаемой током.