Условие
записать уравнение с угловым и коэффициентом в отрезках и нормальное для данных прямых и определите На каком расстоянии от начала координат они находятся 2x-3y+6=0
Решение
2x-3y+6=0 — общее уравнение прямой с нормальным вектором vector=(2;-3)
y=[m]frac[/m]*x+2 — уравнение с угловым коэффициентом
[m]frac+frac=1[/m] — уравнение в отрезках
Делим общее уравнение прямой на [m]sqrt[/m]
По формуле расстояния от точки до прямой:
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение прямых 2x 3y 6
Построить прямые: а) x + 2y — 4 = 0; б) 2x — 3y + 6 = 0.
а) Определим точки пересечения прямой x + 2y — 4 = 0 с координатными осями. Взяв в этом уравнении сначала y = 0, найдем из него, что точка A пересечения прямой с осью Ox имеет абсциссу x = 4. Координаты точки A(4, 0). Положив теперь в уравнении x = 0, найдем, что точка B пересечения прямой с осью Oy имеет ординату y = 2. Координаты точки B(0, 2). Построив эти точки, соединим их прямой (см. рисунок, а). Эта прямая и соответствует данному уравнению.
б) Определим точки пересечения прямой 2x — 3y + 6 = 0 с координатными осями: при y = 0 получаем 2x + 6 = 0, x = -3. Точка A пересечения прямой с осью Ox имеет координаты (-3, 0); при x = 0 имеем -3y + 6 = 0; y = 2, и прямая пересекает ось Oy в точке B(0, 2). Построим эти точки, соединим их прямой и получим прямую, соответствующую данному уравнению (см. рисунок, б).
Видео:№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать

Расстояние между прямыми на плоскости онлайн
С помощю этого онлайн калькулятора можно найти расстояние между прямыми на плоскости. Дается подробное решение с пояснениями. Для вычисления расстояния между прямыми, задайте вид уравнения прямых («канонический», «параметрический» или «общий»), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Расстояние между прямыми на плоскости − теория, примеры и решения
- Содержание
- 1. Расстояние между прямыми в каноническом виде.
- 2. Расстояние между прямыми в общем виде.
1. Расстояние между прямыми в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2:
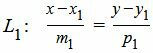 . . | (1) |
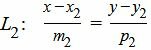 , , | (2) |
Прямые (1) и (2) могут совпадать, быть паралленьными или пересекаться. Если прямые пересекаются, то понятие расстояния между ними не имеет смысла (не определено). Если прямые совпадают, то расстояние между ними равно нулю. Если же они параллельны, то расстояние между ними можно вычислить следующими методами:
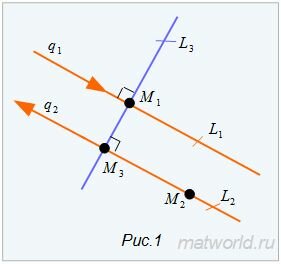 |
Рассмотрим этот метод подробнее. Каноническое уравнение прямой L3, проходящей через точку M1(x1, y1) имеет следующий вид:
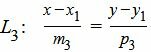 , , | (3) |
Для того, чтобы прямая L3 была перпендикулярна прямой L2, направляющие векторы этих прямых должны быть ортогональны, т.е. скалярное произведение этих векторов должен быть равным нулю:
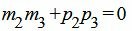 , , | (4) |
Так как направляющий вектор прямой не может быть равным нулю, то предположим, что координата m2 вектора q2 отлична от нуля. Тогда в качестве вектора q3 можно взять вектор q3=<m3, p3>=<p2, −m2>. Следовательно, уравнение прямой L3 получит следующий вид:
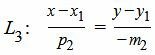 , , | (5) |
Для вычисления координат точки пересечения прямых L2 и L3, решим систему линейных уравнений (2) и (5). Преобразуем эти уравнения сделав перекрестное умножение:
| p2(x−x2)=m2(y−y2) |
| p3(x−x1)=m3(y−y1) |
Откроем скобки и перенесем налево переменную y:
| p2x−m2y=p2x2−m2y2 | (6) |
| p3x−m3y=p3x1−m3y1 | (7) |
Запишем (6) и (7) в матричном виде:
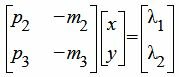 , , | (8) |
| λ1=p2x2−m2y2, | (9) |
| λ2=p3x1−m3y1. | (10) |
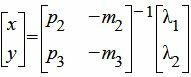 , , | (11) |
Для построения обратной матрицы воспользуемся методом алгебраических дополнений. Сначала вычислим определитель матрицы:
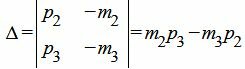 . . |
Тогда обратная матрица примет следующий вид:
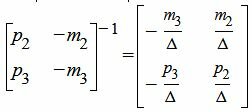 . . | (12) |
Подставляя значение обратной матрицы (12) в (11), получим:
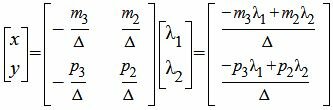 . . |
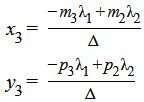 . . | (13) |
Расстояние между точками M1 и M3 равно:
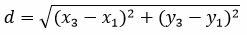 . . | (14) |
Полученное расстояние d также является расстоянием между прямыми L1 и L2.
Пример 1. Найти расстояние между прямыми L1 и L2:
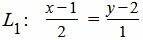 | (15) |
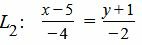 | (16) |
Пользуясь формулой (5), построим уравнение прямой L3, проходящей через точку M1 и перпендикулярной прямой L2:
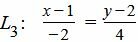 | (17) |
Для вычисления координат точки пересечения прямых L2 и L3, решим систему линейных уравнений (16) и (17). Преобразуем эти уравнения сделав перекрестное умножение:
Сделаем эквивалентные преобразования:
| −2x+4y=−10−4 | (18) |
Запишем систему линейных уравнений (18)-(19) в матричном виде:
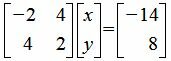 |
Вычислим вектор (x, y) T :
 |
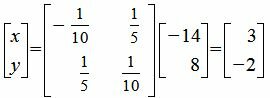 |
Получили точку M3(x3, y3)=(3, −2), которая является точкой пересечения прямых L2 и L3. Расстояние между прямыми L1 и L2 равно расстоянию между точками M1 и M3. Вычислим это расстояние:
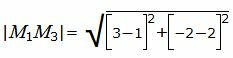 |
 |
Ответ: Расстояние между прямыми L1 и L2 равно d=4.47213595.
Метод 2. Найдем расстояние между прямыми L1 и L2 (уравнения (1) и (2)). Уравнение прямой L3 в общем виде, проходящей через точку M1 и перпендикулярной прямой L2 имеет следующий вид:
| A3(x−x1)+B3(y−y1)=0. | (20) |
Для того, чтобы прямая L3 была перпендикулярна прямой L2, нормальный вектор n3=<A3, B3> прямой L3 должен быть коллинеарным направляющему вектору q2 прямой L2. Поэтому в качестве нормального вектора прямой L3 можно взять вектор q2=<m2, p2>. Подставим координаты вектора q2 в (20):
| m2(x−x1)+p2(y−y1)=0. |
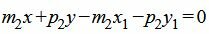 | (21) |
Приведем уравнение прямой (2) к параметрическому виду:
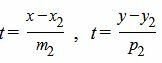 |
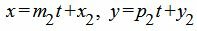 | (22) |
Подставим (22) в (21) и решим относительно t:
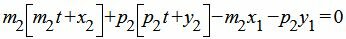 |
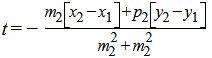 | (23) |
Мы получили такое значение t, при котором соответствующая точка на прямой L2 удовлетворяет уравнению прямой L3, т.е. находится на этой прямой (является точкой пересечения прямых L2 и L3). Подставляя значение t в (22), получим координаты точки M3(x3, y3). Далее вычисляем расстояние между точками M1 и M3:
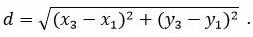 | (24) |
Пример 2. Найти расстояние между прямыми
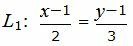 | (25) |
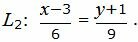 | (26) |
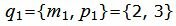 |
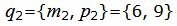 |
Уравнение прямой L3, проходящей через точку M1 и имеющий нормальный вектор n3=<A3, B3> представляется формулой:
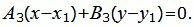 | (27) |
Для того, чтобы прямая L3 была перпендикулярна прямой L2, нормальный вектор n3=<A3, B3> прямой L3 должен быть коллинеарным направляющему вектору q2 прямой L2. Поэтому в качестве нормального вектора прямой L3 можно взять вектор q2=<m2, p2>=. Подставим координаты вектора q2 и координаты точкиM1 в (27):
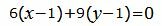 |
После упрощения получим уравнение прямой L3, проходящей через точку M1 и перпендикулярной прямой L2:
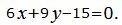 | (28) |
Для нахождения точки пересечения прямых L2 и L3 проще всего пользоваться параметрическим уравнением прямой L2. Составим параметрическое уравнение прямой L2:
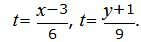 |
Выразим переменные x, y через параметр t :
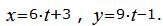 | (29) |
Подставим значения x, y из выражения (29) в (28) и решим относительно t:
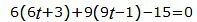 |
 |
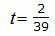 |
Подставляя значение t в выражения (29), получим координаты точки M3:
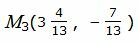 |
Вычислим расстояние между точками M1 и M3
 |
 |
Ответ. Расстояние между прямыми L1 и L2 равно:
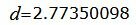 |
2. Расстояние между прямыми в общем виде.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы параллельные прямые L1 и L2:
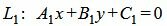 | (30) |
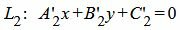 | (31′) |
где n1=<A1, B1> и n2=<A2, B2> − направляющие векторы прямых L1 и L2, соответственно. Так как прямые параллельны, то можно один из них умножить на какое-то число так, чтобы нормальные векторы этих прямых совпадали. Пусть A2≠0. Умножим (31′) на A1/A’2. Тогда уравнение (2′) примет следующий вид:
 | (31) |
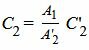 |
Покажем, что расстояние между прямыми L1 и L2 равно:
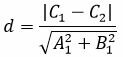 | (32) |
Метод 1. Пусть A1≠0. Тогда точка M1(x1, y1)=M1(−C1/A1, 0) принадлежит прямой L1. Это легко проверить, подставив координаты точки M1 в (30). Построим уравнение прямой, проходящей через точку M1 и перпендикулярной прямой L2:
| A3(x−x1)+B3(y−y1)=0 |
Поскольку прямая L3 перпендикулярна прямой L2, то нормальные векторы этих прямых ортогональны. Тогда вместо нормального вектора n3=<A3, B3> прямой L3 можно взять вектор, ортогональный нормальному вектору n2, т.е. вектор n3=<B1, −A1> (так как скалярное произведение этих векторов равно нулю). Тогда имеем:
| B1(x−x1)−A1(y−y1)=0 | (33) |
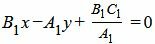 | (34) |
Найдем точку пересечения прямых L2 и L3. Для этого решим систему линейных уравнений (31),(34), представляя в матричном виде:
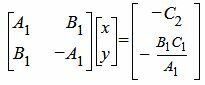 |
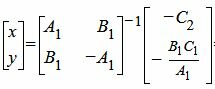 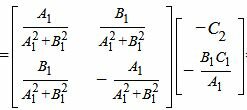  |
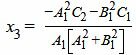 , , 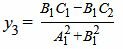 |
 |
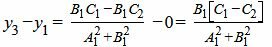 |
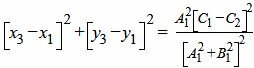 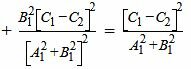 |
Наконец, расстояние между точками M1 и M3, и следовательно, расстояние между прямыми L1 и L2 равно:
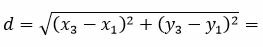 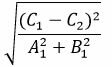 |
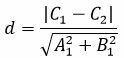 | (35) |
Метод 2. Воспользуемся понятием отклонения точки от прямой. Пусть M1(x1, y1) точка, принадлежащая прямой (30), Тогда выполняется равенство
| A1x1+B1y1+C1=0. | (35) |
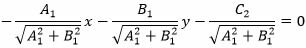 |
При С2 Пример 3. Найти расстояние между прямыми
| L1: x1+2y1−2=0, |
| L2: x1+2y1+6=0, |
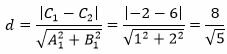 |
Ответ. Расстояние между прямыми L1 и L2 равно:
📹 Видео
9 класс, 7 урок, Уравнение прямойСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

How to Graph the Linear Equation 2x - 3y = 6Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

How do you write 2x-3y=6 in slope-intercept form?Скачать

Составляем уравнение прямой по точкамСкачать

Графическое уравнение [5] — пошаговое решение по алгеб...Скачать
![Графическое уравнение [5] — пошаговое решение по алгеб...](https://i.ytimg.com/vi/d38xsjNUQCo/0.jpg)
Как построить график линейной функции.Скачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Уравнение прямой. Урок 6. Геометрия 9 классСкачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

How to Graph the Linear Equation 3y =2x - 6Скачать

Линейное уравнение с двумя переменными. 7 класс.Скачать
