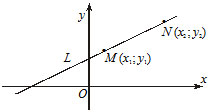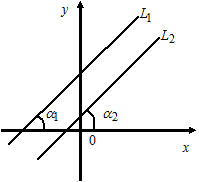В данной статье мы рассмотрим нормальное уравнение прямой на плоскости. Приведем примеры построения нормального уравнения прямой по углу наклона нормального вектора прямой от оси Ox и по расстоянию от начала координат до прямой. Представим метод приведения общего уравнения прямой к нормальному виду. Рассмотрим численные примеры.
Пусть на плоскости задана декартова прямоугольная система координат. Тогда нормальное уравнение прямой L на плоскости представляется следующей формулой:
| xcosφ+ysinφ−r=0, | (1) |
где r− расстояние от начала координат до прямой L, а φ− это угол между нормальным вектором n прямой L и осью Ox. (Если r>0, то нормальный вектор n направлен в сторону прямой L).
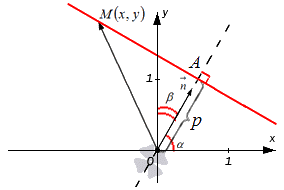
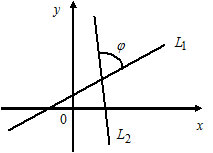
Выведем формулу (1). Пусть на плоскости задана декартова прямоугольная система координат и прямая L (Рис.1). Проведем через начало координат прямую Q, перпендикулярную прямой L, и точку пересечения обозначим через R. На этой прямой выделим единичный вектор n, с направлением, совпадающим с вектором 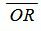
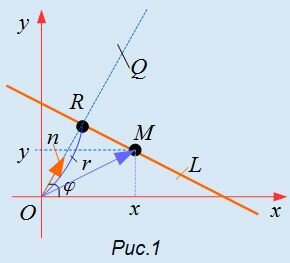 |
Выразим уравнение прямой L через два параметра: длину отрезка 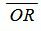
Так как вектор n является единичным вектором, то его проекции на Ox и Oy будут иметь следующие координаты:
| n=<cosφ, sinφ>. | (2) |
Обозначим через r расстояние от начала координат до точки R. Рассмотрим, теперь, точку M(x,y). Точка M лежит на прямой L тогда и только тогда, когда проекция вектора 
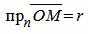 | (3) |
Скалярное произведение векторов n и 
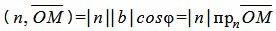 , , | (4) |
где 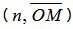


Поскольку n единичный вектор, то (4) можно записать так:
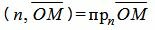 . . | (5) |
Учитывая, что n=<cosφ, sinφ>, 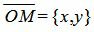
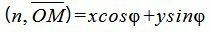 . . | (6) |
Тогда из уравнений (3), (5), (6) следует:
| xcosφ+ysinφ=r |
| xcosφ+ysinφ−r=0. | (7) |
Мы получили нормальное уравнение прямой L. Уравнение (7) (или (1)) называется также нормированным уравнением прямой .
Пример 1. Построить нормальное уравнение прямой, нормальный вектор которого с осью Ox имеет угол φ=60°, а расстояние от начала координат до прямой составляет 4.
Решение. Имеем: φ=60°, r=4. Вычисляем:
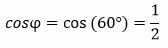 , , 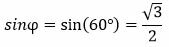 |
Подставляя вычисленные значения в (7) получим:
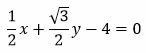 . . |
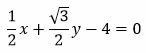 . . |
- Приведение общего уравнения прямой на плоскости к нормальному виду
- Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач
- Нормальное уравнение прямой – описание и пример
- Приведение общего уравнения прямой к нормальному виду
- Математический портал
- Nav view search
- Navigation
- Search
- Аналитическая геометрия.
- Прямая на плоскости, всевозможные уравнения.
- Деление отрезка в заданном отношении (векторный и координатный способы).
- Взаимное расположение плоскостей, угол между плоскостями.
- 📽️ Видео
Видео:Видеоурок "Нормальное уравнение прямой"Скачать

Приведение общего уравнения прямой на плоскости к нормальному виду
Так как уравнения (1) и (8) должны определять одну и ту же прямую (Замечание 1 статьи «Общее уравнение прямой на плоскости»), то существует такое число t, что
| tAx=cosφ, tB=sinφ, tC=−r. | (9) |
Возвышая в квадрат первые два равенства в (9) и складывая их, получим:
| (tA) 2 +(tB) 2 =cos 2 φ+sin 2 φ=1. | (10) |
Упростим выражение и найдем t:
| t 2 A 2 +t 2 B 2 =t 2 (A 2 +B 2 )=1, |
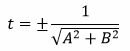 . . | (11) |
Знаменатель в (11) отличен от нуля, т.к. хотя бы один из коэффициентов A, B не равен нулю (в противном случае (8) не представлял бы уравнение прямой).
Выясним, какой знак имеет t. Обратим внимание на третье равенство в (9). Так как r−это расстояние от начала координат до прямой, то r≥0. Тогда произведение tC должна иметь отрицательный знак. Т.е. знак t в (11) должен быть противоположным знаку C.
Подставляя в (1) вместо cosφ, sinφ, и −r значения из (9), получим tAx+tBy+tC=0. Т.е. для приведения общего уравенения прямой к нормальному виду, нужно заданное уравнение умножить на множитель (11). Множитель (11) называется нормирующим множителем .
Пример 2. Задано общее уравнение прямой
Построить нормальное уравнение прямой.
Решение. Из уравнения (12) можно записать: A=2, B=−3, C=4. Вычислим t из равенства (11):
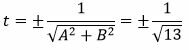 |
Так как C>0, то знак t отрицательный:
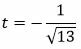 |
Умножим уравнение (12) на t:
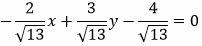 |
Ответ. Нормальное уравнение прямой (12) имеет следующий вид:
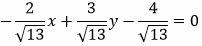 |
Отметим, что число 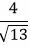
Видео:Геометрия. 9 класс. Уравнение прямой. Направляющий вектор и вектор нормали прямой /22.10.2020/Скачать

Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач
В данной статье рассмотрим нормальное уравнение прямой на заданной плоскости. Получим нормальное уравнение, покажем не примере, дадим определение нормирующего множителя и разберем приведение общего уравнения к нормальному виду. Заключительной части посвятим основному приложению нормального уравнения прямой, то есть нахождение расстояние от точки до прямой на плоскости.
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Нормальное уравнение прямой – описание и пример
Рассмотрим выведение нормального уравнения.
Фиксируем на плоскости систему координат О х у , где задаем прямую с точкой, через которую она проходит с нормальным вектором прямой. Нормальному вектору прямой дадим обозначение n → . Его начало обозначено точкой O . координатами являются cos α и cos β , углы которых расположены между вектором n → и положительными осями О x и O y . Это запишется так: n → = ( cos α , cos β ) . Прямая проходит через точку A с расстоянием равным p , где p ≥ 0 от начальной точки O при положительном направлении вектора n → . Если р = 0 , тогда A считается совпадающей с точкой координат. Отсюда имеем, что O A = p . Получаем уравнение, при помощи которого задается прямая.
Имеем, что точка с координатами M ( x , y ) расположена на прямой тогда и только тогда, когда числовая проекция вектора O M → по направлению вектора n → равняется p , значит при выполнении условия n p n → O M → = p .
O M → является радиус-вектором точки с координатами M ( x , y ) , значит O M → = ( x , y ) .
Применив определение скалярного произведения векторов, получим равенство вида: n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → = p
Тогда это же произведение будет иметь вид в координатной форме: n → , O M → = cos α · x + cos β · y
Отсюда cos α · x + cos β · y = p или cos α · x + cos β · y — p = 0 . Было выведено нормальное уравнение прямой.
Уравнение вида cos α · x + cos β · y — p = 0 называется нормальным уравнением прямой или нормированным уравнением прямой. Иначе говоря, уравнение прямой в нормальном виде.
Понятно, что такое уравнение представляет собой общее уравнение прямой A x + B y + C = 0 , где A и B имеют значения, при которых длина вектора n → = ( A , B ) равна 1 , а C является неотрицательным числом.
Теперь рассмотрим его геометрический смысл. Нормальное уравнение прямой вида cos α · x + cos β · y — p = 0 задает в системе координат О х у на плоскости прямую с наличием нормального вектора единичной длины n → = ( cos α , cos β ) , которая располагается на расстоянии равном p от начала координат по положительному направлению вектора n → .
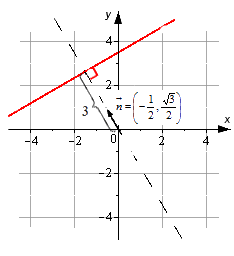
Если дано уравнение прямой вида — 1 2 · x + 3 2 · y — 3 = 0 , то на плоскости задается прямая, у которой нормальный вектор с координатами — 1 2 , 3 2 . Удаление прямой от начала координат идет по направлению, совпадающему с направлением нормального вектора n → = — 1 2 , 3 2 .
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Приведение общего уравнения прямой к нормальному виду
Часто решение задач подразумевает использование нормального уравнения прямой, но само оно не дается в нормальном виде, поэтому необходимо для начала приводить к нормальному виду, после чего выполнять необходимые вычисления.
Нормальное уравнение получают из общего уравнения прямой. Когда на плоскости задается другим уравнением, то необходимо привести его к общему виду, после чего возможно приведение к нормальному. Если рассмотреть на примере, то это будет выглядеть так.
Для приведения общего уравнения прямой A x + B x + C = 0 к нормальному необходимо обе части умножить на нормирующий множитель, который имеет значение ± 1 A 2 + B 2 . Его знак определяется при помощи противоположности знака слагаемого C . При С = 0 знак выбирается произвольно.
Привести уравнение прямой 3 x — 4 y — 16 = 0 к нормальному виду.
Из общего уравнения видно, что А = 3 , В = — 4 , С = — 16 . Так как значение C отрицательное, необходимо брать положительный знак для формулы. Перейдем к вычислению нормирующего множителя:
1 A 2 + B 2 = 1 3 2 + ( — 4 ) 2 = 1 5
Теперь необходимо умножить обе части уравнения на одну пятую. Получим, что 1 5 · ( 3 x — 4 y — 16 ) = 0 ⇔ 3 5 · x — 4 5 · y — 16 5 = 0 .
Нормальное уравнение по заданной прямой найдено.
Ответ: 3 5 · x — 4 5 · y — 16 5 = 0 .
Видео:Направляющий и нормальный вектор прямой на плоскости | Векторная алгебраСкачать

Математический портал
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Nav view search
Navigation
Search
- Вы здесь:
- Home
- Векторная алгебра
- Высшая математика.
- Аналитическая геометрия.
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Аналитическая геометрия.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Прямая на плоскости, всевозможные уравнения.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Существуют такие формы записи уравнения прямой:
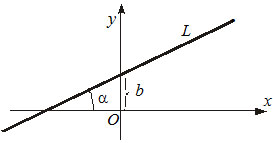
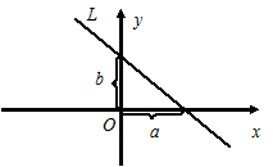
1) $y=kx+b,$ где $k -$ угловой коэффициент, $b-$ отрезок, который прямая отсекает на оси $OY.$
2) $y-y_0=k(x-x_0) $ — уравнение прямой, которая проходит через заданную точку $P(x_0, y_0)$ под заданным углом $alpha$ к оси $OX$ $(k=tgalpha).$
3) $frac=frac $ — уравнение прямой, которая проходит через две точки $M(x_1, y_1)$ и $N(x_2, y_2).$
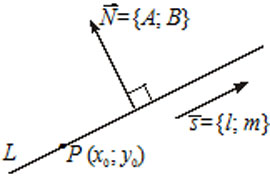
5) $frac=frac $ — каноническое уравнение прямой, где $overline=(l, m) -$ направляющий вектор прямой, то есть вектор параллельный прямой $(overlineparallel L),$ точка $P(x_0, y_0)in L.$
6) $A(x-x_0)+B(y-y_0)=0$ — уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0)$ перпендикулярно вектору $overline=(A, B).$ Вектор $overline N$ называется нормальным вектором прямой.
7) $Ax+By+C=0 -$ общее уравнение прямой $L,$ где $overline=(A, B) -$ нормальный вектор прямой $L.$
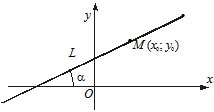
8) $xcosalpha+ycosbeta-p=0 -$ нормальное уравнение прямой, где $cosalpha$ и $cosbeta -$ направляющие косинусы нормального вектора $n,$ направленного из начала координат в сторону прямой, а $p>0 -$ расстояние от начала координат до прямой.
Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $mu=-frac<sqrt>.$
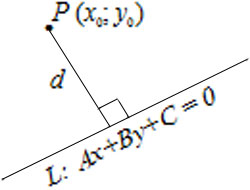
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$
Расположение двух прямых на плоскости.
Условия параллельности двух прямых:
1) Пусть $L_1: k_1x+b_1,$ $k_1=tgalpha_1;$
$L_2: k_2x+b_2,$ $k_2=tgalpha_2.$
Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $k_1=k_2.$
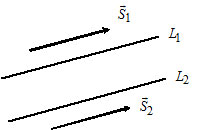
2) Пусть $L_1:$ $frac=frac,$ $overline_1=(l_1, m_1);$
Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $overline_1paralleloverline_2Leftrightarrow$ $frac=frac.$
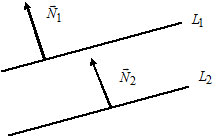
3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $overline_1=(A_1, B_1);$
$L_2: A_2x+B_2y+C_2=0,$ $overline_2=(A_2, B_2).$
Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $overline_1paralleloverline_2Leftrightarrow$ $frac=frac.$
Условия перпендикулярности двух прямых:
1) Пусть $L_1: k_1x+b_1,$ $k_1=tgalpha_1;$
$L_2: k_2x+b_2,$ $k_2=tgalpha_2.$
$L_1perp L_2Leftrightarrow$ $k_1cdot k_2=-1.$
2) Пусть $L_1:$ $frac=frac,$ $overline_1=(l_1, m_1);$
$L_1perp L_2Leftrightarrow$ $overline_1perpoverline_2Leftrightarrow$ $cdot+cdot=0.$
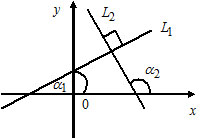
3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $overline_1=(A_1, B_1);$
$L_2: A_2x+B_2y+C_2=0,$ $overline_2=(A_2, B_2).$
$L_1perp L_2Leftrightarrow$ $overline_1perpoverline_2Leftrightarrow$ $cdot+cdot=0.$
Угол между прямыми:
1) Пусть $L_1: k_1x+b_1,$ $k_1=tgalpha_1;$
$L_2: k_2x+b_2,$ $k_2=tgalpha_2.$
2) Пусть $L_1:$ $frac=frac,$ $overline_1=(l_1, m_1);$
3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $overline_1=(A_1, B_1);$
$L_2: A_2x+B_2y+C_2=0,$ $overline_2=(A_2, B_2).$
Примеры:
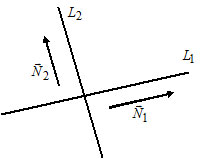
2.141.
а) Прямая $L$ задана точкой $M_0(-1; 2)in L$ и нормальным вектором $overline N(2; 2).$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.
Решение.
Подставим в формулу 6) для уравнения прямых ( $A(x-x_0)+B(y-y_0)=0$ ) соответственно координаты точки $(x_0; y_0)=M_0(-1; 2)$ и вектора $(A; B)=overline N(2; 2):$
$2(x+1)+2(y-2)=0.$ Далее, приведем это уравнение к общему виду:
Нормальное уравнение прямой имеет вид $xcosalpha+ycosbeta-p=0,$ где $cosalpha$ и $cosbeta -$ направляющие косинусы нормального вектора $n,$ направленного из начала координат в сторону прямой, а $p>0 -$ расстояние от начала координат до прямой.
Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $mu=-frac<sqrt>.$
Для нашей прямой имеем $A=1; B=1; C=-1 Rightarrow sgn C=-1.$ Таким образом, $mu=-frac<sqrt>=frac.$
Запишем нормальное уравнение прямой:
Расстояние от начала координат $p=frac.$
Ответ: $2(x+1)+2(y-2)=0;$ общее уравнение $x+y-1=0;$ нормальное уравнение прямой $fracx+fracy-frac=0;$ $p=frac.$
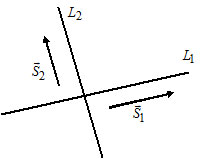
2.142.
а) Прямая $L$ задана точкой $M_0(-1; 2)in L$ и направляющим вектором $overline S(3; -1).$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.
Решение.
Подставим в формулу 5) для уравнения прямых ( $frac=frac$ ) соответственно координаты точки $(x_0; y_0)=M_0(-1; 2)$ и вектора $(l; m)=overline S(3; -1):$ $frac=frac$
Далее, приведем это уравнение к общему виду:
Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $mu=-frac<sqrt>.$
Для нашей прямой имеем $A=1; B=3; C=-5 Rightarrow sgn C=-1.$ Таким образом, $mu=-frac<sqrt>=frac<sqrt>.$
Запишем нормальное уравнение прямой:
Расстояние от начала координат $p=frac<sqrt >.$
Ответ: $frac=frac;$ общее уравнение $x+3y-5=0;$ нормальное уравнение прямой $frac<sqrt >x+frac<sqrt >y-frac<sqrt >=0;$ $p=frac<sqrt >.$
2.143.
а) Прямая $L$ задана двумя своими точками $M_1(1; 2)in L$ и $M_2(-1; 0)in L.$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.
Решение.
Подставим в формулу 3) для уравнения прямых ($frac=frac$ ) соответственно координаты точек $M_1(1; 2)= (x_1; y_1) $ и $M_2(-1; 0)=(x_2; y_2):$ $frac=fracRightarrow frac=frac.$
Далее, приведем это уравнение к общему виду:
Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $mu=-frac<sqrt>.$
Для нашей прямой имеем $A=1; B=-1; C=1 Rightarrow sgn C=1.$ Таким образом, $mu=-frac<sqrt>=-frac<sqrt>.$
Запишем нормальное уравнение прямой:
Расстояние от начала координат $p=frac<sqrt >.$
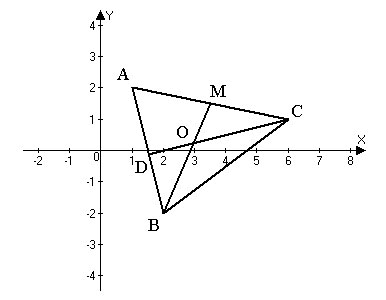
2.150. Треугольник $ABC$ задан координатами своих вершин $A(1; 2), B(2; -2), C(6; 1).$ Требуется:
1) Найти уравнение стороны $AB;$
2) найти уравнение высоты $CD$ и вычислить ее длину $h=|CD|;$
3) найти угол между высотой $CD$ и медианой $BM.$
Решение.
1) Уравнение прямой $AB$ найдем по формуле уравнения прямой, проходящей через две точки $frac=frac. $
В нашем случае $(x_1; y_1)=A(1; 2);$ $(x_2; y_2)=B(2; -2).$
Подставляем координаты точек в уравнение прямой. Получаем $$frac=fracRightarrow x-1=frac.$$ Запишем общее уравнение прямой $AB$:
$-4(x-1)=y-2Rightarrow$ $-4x+4=y-2Rightarrow$ $4x+y-6=0.$
2) Уравнение прямой $CD$ найдем, пользуясь уравнением ( 6): $A(x-x_0)+B(y-y_0)=0$ — уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0)$ перпендикулярно вектору $overline=(A, B).$
В нашем случае, высота $CD$ это прямая, которая проходит через точку $C$ перпендикулярно вектору $AB.$
Таким образом, $$(x_0; y_0)=C=(6; 1);quadoverline=overline=(2-1; -2-2)=(1; -4).$$
Подставляем эти координаты в уравнение прямой:
$1(x-6)-4(y-1)=0Rightarrow x-6-4y+4=0 Rightarrow x-4y-2=0.$
То есть, уравнение прямой $CD:$ $x-4y-2=0.$
Чтобы найти длину высоты $h=|CD|,$ найдем координаты точки $D,$ как точки пересечения прямых $CD$ и $AB:$
Решим систему методом исключений:
Следовательно имеем $D(26/17; -2/17).$ Теперь можем найти длину высоты $CD:$
3) Уравнение высоты $CD$ мы уже нашли в пункте 2). Найдем уравнение медианы $BM.$ Будем его искать, используя форумулу уравнения прямой, проходящей через две точки.
Координаты точки $B=(2, -2); $ координаты точки $M$ найдем как середину стороны $AC:$ $x_M=frac; y_M=frac.$
Подставляем координаты точек $B(2; -2)$ и $M(3.5; 1.5)$ в уравнение прямой
$3.5(x-2)=1.5(y+2)Rightarrow 3.5x-7=1.5y+3 Rightarrow 3.5x-1.5y-10=0.$
Далее, зная общие уравнения двух прямых $CD: x-4y-2=0$ и $BM: 3.5x-1.5y-10=0$ можно найти угол между ними по формуле
где $L_1: A_1x+B_1y+C_1=0,$ $overline_1=(A_1, B_1);$
$L_2: A_2x+B_2y+C_2=0,$ $overline_2=(A_2, B_2).$
Для наших прямых имеем: $(A_1, B_1)=(1; -4);$ $(A_2; B_2)=(3.5; -1.5).$
Ответ: 1) $AB: 4x+y-6=0.$
2.160. В равнобедренном треугольнике $ABC$ заданы вершина $C(4; 3),$ уравнение $2x-y-5=0$ основания $AC$ и уравнение $x-y=0$ боковой стороны $AB.$ Найти уравнение стороны $BC.$
Решение.
Найдем координаты вершины треугольника $A,$ как точки пересечения прямых $AB$ и $AC:$
Таким образом, мы имеем координаты вершин при основании равнобедренного треугольника $A(5; 5)$ и $C(4; 3).$ Найдем координаты вершины $B(x, y).$ Мы знаем, что эта точка принадлежит прямой $AB: x-y=0$ и что $AB=BC.$ Запишем формулы для длин сторон $AB$ и $BC:$
Далее, чтобы найти координаты точки $B,$ решим систему уравнений:
$$Rightarrowleft<beginx=y\y=frac.endright.$$ Мы нашли координаты точки $Bleft(frac, fracright).$
Зная координаты точек $B$ и $C$ можно записать уравнение прямой $BC,$ как прямой проходящей через две точки $left(frac=frac right):$
$$Rightarrowfrac=fracRightarrow 7x-28=y-3Rightarrow 7x-y-25=0.$$
Ответ: $7x-y-25=0.$
2.165. Даны две противоположные вершины квадрата $A(1; 3)$ и $C(-1; 1).$ Найти координаты двух его других вершин и написать уравнения его сторон.
Решение:
Найдем уравнение диагонали $AC:$
Далее, найдем уравнение второй диагонали квадрата — прямой, проходящей через точку $O$ перпендикулярно прямой $AC.$ Для прямой $AC$ нормальный вектор имеет координаты $overline=(1; -1).$ Прямая, перпендикулярная прямой $AC$ является параллельной нормальному вектору $overline$. Таким образом, уравнение прямой $BD$ запишем по формуле 5) $left(frac=fracright),$ где $(x_0, y_0)=O(0; 2),$ $(l, m)=overline=(1, -1):$
$$frac=fracRightarrow x=-y+2 Rightarrow x+y-2=0.$$
Ясно, что $AO=CO=BO=DO.$ Найдем длину отрезка $AO:$ $AO=sqrt=sqrt.$
Далее, будем искать координаты точек $B$ и $D,$ принадлежащих прямой $BD$ и таких, что $BO=DO=AO.$
Таким образом, мы нашли координаты вершин $B(1; 1)$ и $D(-1; 3).$ Зная координаты вершин квадрата, запишем уравнения его сторон, пользуясь формулой ( 3) — $frac=frac $ — уравнение прямой, которая проходит через две точки $M(x_1, y_1)$ и $N(x_2, y_2).$
Ответ: $A(1; 3),$ $B(1; 1),$ $C(-1; 1),$ $D(-1; 3);$ $AB:$ $x=1;$ $BC:$ $y=1;$ $CD:$ $x=-1;$ $DA:$ $y=3.$
Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Деление отрезка в заданном отношении (векторный и координатный способы).
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Зная координаты точек $M_1(x_1, y_1, z_1)$ и $M_2(x_2, y_2, z_2)$ и отношение $lambda,$ в котором точка $M$ делит направленный отрезок $overline,$ найдем координаты точки $M.$
Пусть $O -$ начало координат. Обозначим $overline=r_1,$ $overline=r_2,$ $overline=r.$ Так как, $$overline=r-r_1, overline=r_2-r,$$ то $r-r_1=lambda(r_2-r),$ откуда (так как $lambdaneq -1$) $$r=frac.$$ Полученная форма и дает решение задачи в векторной форме. Переходя в этой формуле к координатам, получим $$x=frac, y=frac, z=frac.$$
Примеры.
2.57. Отрезок с концами в точках $A(3, -2)$ и $B(6, 4)$ разделен на три равные части. Найти координаты точек деления.
Решение.
Пусть $C(x_C, y_C)$ и $D(x_D, y_D) -$ точки, которые делят отрезок $AB$ на три равные части. Тогда $$lambda_1=frac=frac;$$ $$x_C=frac=frac<3+fraccdot 6><1+frac>=4;$$
Далее находим координаты точки $D:$
Ответ: $(4, 0)$ и $(5, 2).$
2.58. Определить координаты концов отрезка, который точками $C(2, 0, 2)$ и $D(5, -2, 0)$ разделен на три равные части.
Решение.
Пусть $A(x_A, y_A, z_A)$ и $B(x_B, y_B, z_B) -$ концы заданного отрезка.
Выпишем формулы для нахождения координат точки $C$ и подставим известные координаты:
Аналогичные равенства запишем для точки $D:$
Далее запишем полученные уравнения относительно $x_A, x_B;$ $y_A, y_B$ и $z_A, z_B$ попарно в виде систем и решим их:
Таким образом, получили координаты концов отрезка $A(-1, 2, 4)$ и $B(8, -4, -2).$
Ответ: $A(-1, 2, 4),$ $B(8, -4, -2).$
Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать

Взаимное расположение плоскостей, угол между плоскостями.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Условие параллельности двух плоскостей:
Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline_1=(A_1, B_1, C_1);$
$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline_2=(A_2, B_2, C_2).$
Плоскости $P_1$ и $P_2$ параллельны тогда и только тогда, когда $overline_1paralleloverline_2Leftrightarrow$ $frac=frac=frac.$
Условия перпендикулярности двух плоскостей:
Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline_1=(A_1, B_1, C_1);$
$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline_2=(A_2, B_2, C_2).$
$P_1perp P_2Leftrightarrow$ $overline_1perpoverline_2Leftrightarrow$ $cdot+cdot+C_1cdot C_2=0.$
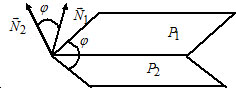
Угол между плоскостями:
Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline_1=(A_1, B_1, C_1);$
$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline_2=(A_2, B_2, C_2).$
Примеры.
В задачах исследовать взаимное расположение заданных плоскостей. При этом, в случае $P_1parallel P_2$ то найти расстояние между плоскостями, а в случае — косинус угла между ними.
2.185. $P_1: -x+2y-z+1=0;$ $P_2: y+3z-1=0.$
Решение.
Вычислим угол между заданными плоскостями.
$P_1: -x+2y-z+1=0, Rightarrowoverline_1=(-1, 2, -1);$
$P_2: y+3z-1=0, Rightarrowoverline_2=(0, 1, 3).$
Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями
Ответ: Плоскости пересекаются. $coswidehat=frac<2sqrt>.$
Решение.
Вычислим угол между заданными плоскостями.
$P_1: x-y+1=0, Rightarrowoverline_1=(1, -1, 0);$
$P_2: y-z+1=0, Rightarrowoverline_2=(0, 1, -1).$
Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями
Ответ: Плоскости пересекаются. $coswidehat=frac.$
2.196. Составить уравнение плоскости $P,$ проходящей через точку $A(1, 1, -1)$ и перпендикулярной к плоскостям $P_1: 2x-y+5z+3=0$ и $P_2: x+3y-z-7=0.$
Решение.
Для того, чтобы плоскость $P$ была перпендикулярно плоскостям $P_1$ и $P_2,$ достаточно, чтобы она была параллельна их нормалям $N_1$ и $N_2.$ Или, что тоже самое, перпендикулярна векторному произведению $[N_1, N_2]$
$P_1: 2x-y+5z+3=0, Rightarrowoverline_1=(2, -1, 5);$
$P_2: x+3y-z-7=0, Rightarrowoverline_2=(1, 3, -1).$
Теперь выпишем уравнение плоскости, проходящей через заданную точку $A(1, 1, -1)$ и перпендикулярной вектору $[N_1, N_2]=(-14, 7, 7):$
Ответ: $-2x+y+z+2=0.$
Домашнее задание.
В задачах исследовать взаимное расположение заданных плоскостей. При этом, в случае $P_1parallel P_2$ то найти расстояние между плоскостями, а в случае — косинус угла между ними.
📽️ Видео
Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Видеоурок "Общее уравнение прямой"Скачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Видеоурок "Общие уравнения прямой"Скачать

11. Прямая в пространстве и ее уравненияСкачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

12. Уравнения прямой в пространстве Решение задачСкачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

Видеоурок "Параметрические уравнения прямой"Скачать