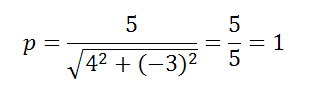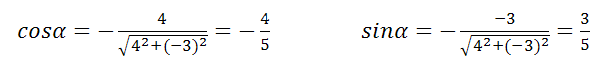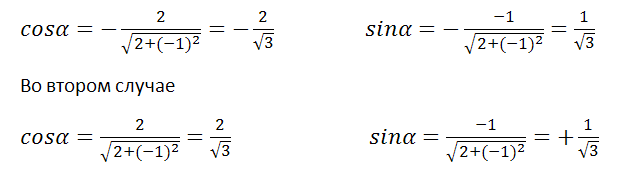Уравнение прямой в полярной системе координат имеет вид (2 видео)

Содержание

Прямая в полярных координатах
Прямая в полярных координатах вне полюса
Прямая в полярных координатах проходящая через полюс
Полярное уравнение и параметры прямой
4.4. Уравнение линии в полярных координатах
🔍 Видео

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Прямая в полярных координатах

Видео:Полярная система координатСкачать

Прямая в полярных координатах вне полюса

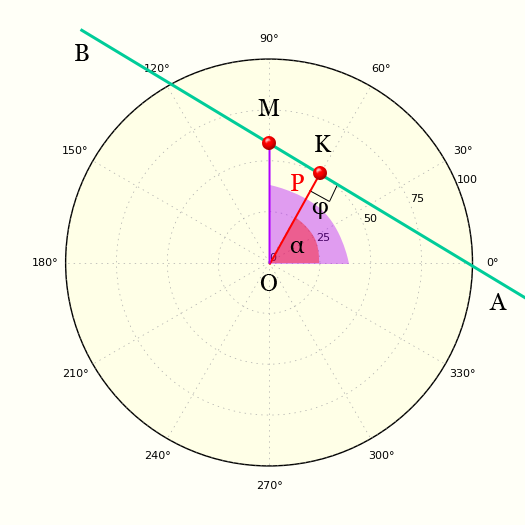
Для получения уравнения прямой в полярных координатах рассмотрим рисунок, на котором полюс лежит вне прямой.

Согласно этого рисунка прямую в полярных координатах можно представить следующим уравнением:

ρ, φ	полярные координаты,
P, α	Константы — полярные параметры прямой,
P	Длина нормали опущенной из полюса на прямую,
α	Угол между полярной осью и нормалью к прямой.

Это уравнение получается если рассмотреть треугольник OKM и посмотреть определение косинуса

Видео:§12 Полярное уравнение прямойСкачать

Прямая в полярных координатах проходящая через полюс

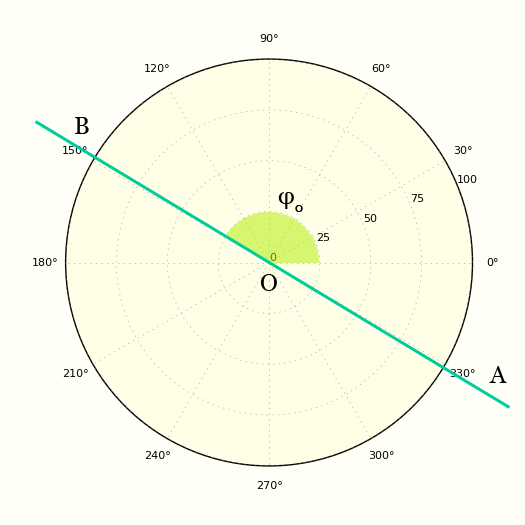
Однако когда P = 0, то прямая проходит через полюс и уравнение (1) больше не описывает прямую. Для описания прямой проходящей через полюс достаточно угла между прямой и полярной осью.

Видео:Построение кривой в полярной системе координатСкачать

Полярное уравнение и параметры прямой

Прямая AB (рисунок ниже)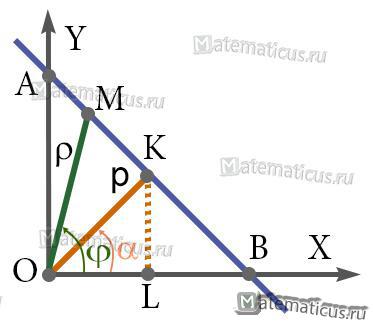

не проходящая через полюс, представляется в полярных координатах уравнением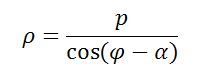

p = OK и α = ∠XOK — полярные параметры прямой AB.

Полярным расстоянием прямой AB называется длина p перпендикуляра OK , проведённого к прямой из начала О . Полярное расстояние положительно или равно нулю.
Полярным углом прямой AB называется угол α=∠XOK между лучами OX и OK (взятым в данном порядке).
Полярное расстояние и полярный угол называются полярными параметрами прямой.

Если прямая представлена уравнением Ax+By+C=0 , то её полярное расстояние определяется по формуле

а полярный угол

где верхние знаки берутся, когда C>0 , а нижние – когда C ; если же С=0 , то произвольно берутся либо только верхние, либо только нижние знаки.

Пример 1
Найти полярные параметры прямой 4x-3y+5=0

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Затем нужно взять верхние знаки, так как С=+1 , следовательно

Видео:Видеоурок "Полярная система координат"Скачать

Пример 2
Найти полярные параметры прямой 2x-y+9=0

Решение
p=0
Можно взять только верхние знаки, либо только нижние. В первом случае

Видео:Полярная система координат.Скачать

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

4.4. Уравнение линии в полярных координатах

По существу, уравнение линии в полярной системе координат представляет собой функцию полярного радиуса от полярного угла (аргумента). При этом полярный угол учитывается в радианах (!) и непрерывно принимает значения от до (иногда следует рассмотреть до бесконечности, или же в ряде задач для удобства от до ). Каждому значению угла «фи», которое входит в область определения функции , соответствует единственное значение полярного радиуса.

Полярную функцию можно сравнить со своеобразным радаром – когда луч света, исходящий из полюса, вращается против часовой стрелки и «прорисовывает» линию.

«Дежурным» примером полярной кривой является Архимедова спираль . На следующем рисунке изображен её первый виток – когда полярный радиус вслед за полярным углом принимает значения от 0 до :
Далее, пересекая полярную ось в точке , спираль продолжит раскручиваться, бесконечно далеко удаляясь от полюса. Но подобные случаи на практике встречаются довольно редко; более типичная ситуация, когда на всех последующих оборотах мы «пройдёмся по той же самой линии», которая получена в диапазоне .
В первом же примере мы сталкиваемся и с понятием области определения полярной функции: поскольку полярный радиус неотрицателен , то отрицательные углы у функции рассматривать нельзя.

! Примечание: в ряде случаев принято использовать обобщённые полярные координаты, где радиус может быть отрицательным, и такой подход мы вкратце изучим чуть позже

Кроме спирали Архимеда, есть множество других известных кривых, но искусством, как говорится, сыт не будешь, поэтому я подобрал примеры, которые очень часто встречаются в реальных практических заданиях.

Сначала простейшие уравнения и простейшие линии:

Уравнение вида задаёт луч, исходящий из полюса. Действительно, вдумайтесь, если значение угла всегда (каким бы ни было «эр») постоянно, то какая это линия?

Примечание: в обобщённой полярной системе координат данное уравнение задаёт прямую, проходящую через полюс.

Уравнение вида определяет… догадайтесь с первого раза – если для любого угла «фи» радиус остаётся постоянным? Фактически это определение окружности с центром в полюсе радиуса .

Например, . Для наглядности найдём уравнение этой линии в прямоугольной системе координат. Используя полученную ранее формулу , проведём замену:

Возведём обе части в квадрат:
– уравнение окружности с центром в начале координат радиуса 2, что и требовалось проверить.

А теперь оценИте удобство – с окружностью значительно выгоднее работать именно в полярных координатах по причине предельной простоты уравнения .

Рассмотрим более содержательные задачи на построение:

Задача 116

Построить линию

Решение: в первую очередь найдём область определения. Так как полярный радиус неотрицателен, то должно выполняться неравенство . Можно вспомнить школьные правила решения тригонометрических неравенств, но в простых случаях как этот,
я советую более быстрый графический метод решения:

– Посмотрим на график функции (см. Приложение Тригонометрия). Что означает неравенство ? Оно означает, что нас устраивает тот кусок графика, который не ниже оси абсцисс , а именно, его часть на отрезке . И, соответственно, интервал не подходит. Таким образом, область определения нашей функции: , то есть график расположен справа от полюса (по терминологии декартовой системы – в правой полуплоскости).

В полярных координатах часто бывает смутное представление о том, какую линию определяет то или уравнение, поэтому чтобы её построить, необходимо найти принадлежащие ей точки – и чем больше, тем лучше. Обычно ограничиваются десятком-другим (а то и меньшим количеством). Проще всего, конечно же, взять табличные значения угла.

Для бОльшей ясности к отрицательным значениям угла я буду «прикручивать» один оборот (левая колонка), и в силу чётности косинуса соответствующие положительные значения можно заново не считать (справа):

Изобразим полярную систему координат и отложим найденные точки, при этом одинаковые значения «эр» удобно откладывать за один раз, делая парные засечки циркулем по рассмотренной ранее технологии:

В принципе, линия отчётливо прорисовывается, но чтобы стопроцентно подтвердить догадку, давайте найдём её уравнение в декартовой системе координат. Можно применить недавно выведенные формулы , но я расскажу вам о более хитром приёме.

Обе части уравнения искусственно домножаем на «эр»: и используем более компактные формулы перехода:

Выделяя полный квадрат, приводим уравнение к понятному виду:

– уравнение окружности с центром в точке , радиуса 2.

Коль скоро по условию требовалось просто выполнить построение и всё, плавно соединяем найденные точки линией. Ничего страшного, если получится немного неровно, вы же не обязаны были знать, что это окружность 😉

Почему мы не рассмотрели значения угла вне промежутка ?

Ответ прост: нет смысла. Ввиду периодичности функции нас ждёт бесконечный «бег» по построенной окружности.

Несложно провести нехитрый анализ и прийти к выводу, что уравнение вида задаёт окружность диаметра с центром в точке .

Образно говоря, все такие окружности «сидят» на полярной оси и обязательно проходят через полюс. Если же , то весёлая компания перекочует налево – на продолжение полярной оси (подумайте, почему).

Похожая задача для самостоятельного решения:

Задача 117

Построить линию и найти её уравнение в декартовой системе координат.

Систематизируем порядок решения задачи:

Находим область определения функции, для этого удобно посмотреть на синусоиду (Приложение Тригонометрия), чтобы сразу же понять, где синус неотрицателен.

На втором шаге рассчитываем полярные координаты точек, используя табличные значения углов; проанализируйте, нельзя ли сократить количество вычислений?

На третьем шаге откладываем точки в полярной системе координат и аккуратно соединяем их линией.

И, наконец, находим уравнение линии в декартовой системе координат.

Примерный образец решения в конце книги.

Общий алгоритм и технику построения в полярных координатах мы детализируем и существенно ускорим совсем скоро, но перед этим познакомимся ещё с одной распространённой линией: