Уравнение прямой в геометрии лобачевского (3 видео)

Геометрия Лобачевского

Пятой аксиомой Евклида была аксиома о параллельных прямых, так называемый постулат о параллельных линиях, который гласит: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны. То есть эта аксиома утверждает, что существует только одна прямая, проходящая через данную точку вне данной прямой и параллельной этой данной прямой.

Сложная формулировка пятого постулата Евклида о параллельных линиях породила множество гипотез и предположений о возможной зависимости его от других постулатов. Были предприняты многочисленные попытки вывести его из остальных аксиом геометрии, но, к сожалению, они оказались тщетны. Усилия доказать пятый постулат от противного также не увенчались успехом.

И все же, в начале XX века почти одновременно несколько выдающихся математиков того времени — Карл Гаусс из Германии, Я. Больяи из Венгрии и Николай Иванович Лобачевский из России пришли к мысли о существовании другой, неевклидовой геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную.

Поскольку Н. И. Лобачевский первым высказал эту идею в 1826 году, новая неевклидова геометрия была названа в его именем.

Геометрия Лобачевского имеет лишь одно отличие от евклидовой — аксиома параллельности заменяется на ее отрицание — аксиому параллельности Лобачевского.

Аксиома параллельности Лобачевского выглядит следующим образом:

Найдутся такая прямая a и такая не лежащая на ней точка A, что через A проходят по крайней мере две прямые, не пересекающие a.

Непротиворечивость аксиомы доказывается представлением модели, в которой реализуются данные аксиомы.

Основы аналитической геометрии, заложенные Лобачевским, практически наметили необходимую для доказательства модель. Лобачевский заметил, что орисфера в пространстве изометрична евклидовой плоскости. Полностью реализовать модель смогли работы Клейна, Пуанкаре и других ученых.

Геометрия Лобачевского нашла широчайшее применение в современной науке. Сам Николай Иванович Лобачевский использовал свою геометрию для вычисления определенных интегралов.

В теории функций комплексного переменного геометрия Лобачевского способствовала успешному построению теории автоморфных функций. В этой теории связь с геометрией Лобачевского была основой для исследований Пуанкаре. По словам Анри Пуанкаре, «неевклидова геометрия есть ключ к решению всей задачи».

Кроме того, геометрия Лобачевского стала использоваться в теории чисел, а именно, в ее геометрических методах, так называемой «геометрии чисел».

Ученые также установили тесную связь геометрии Лобачевского с кинематикой — специальной теорией относительности. В основе этой связи лежит равенство, выражающее закон распространения света:

x 2 + y 2 + z 2 = c 2 t 2 ,

при делении на t 2 , то есть для скорости света, даёт уравнение сферы в пространстве с координатами v_x, v_y, v_z, которые являются составляющими скорости света по осям х, у, z.

Преобразование Лоренца сохраняет эту сферу, а поскольку они линейны, переводят прямые пространства скоростей в прямые. Из этого следует, (согласно модели Клейна) что в пространстве скоростей внутри сферы радиуса с , значит есть для скоростей, меньших скорости света, имеет место геометрия Лобачевского.

В общей теории относительности геометрия Лобачевского также нашла свое место. Допуская возможным тот факт, что распределение масс материи во Вселенной равномерно (это приближение в космических масштабах допустимо), то при определенных условиях пространство имеет геометрию Лобачевского. Тем самым было доказано предположение Лобачевского о новой геометрии как возможной теории пространства.

Содержание

ЛОБАЧЕ́ВСКОГО ГЕОМЕ́ТРИЯ
Модели геометрии Лобачевского
Задача
Подсказка 1
Подсказка 2
Решение
Послесловие
💡 Видео

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

ЛОБАЧЕ́ВСКОГО ГЕОМЕ́ТРИЯ

В книжной версии

Том 17. Москва, 2010, стр. 712-714

Скопировать библиографическую ссылку:

ЛОБАЧЕ́ВСКОГО ГЕОМЕ́ТРИЯ, одна из неевклидовых геометрий, основана на тех же посылках, что и обычная – евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на иную. Евклидова аксиома о параллельных состоит в том, что через точку, не лежащую на данной прямой, проходит не более чем одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её (в евклидовой геометрии такие прямые называют параллельными). В Л. г. эта аксиома заменяется следующей: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её (достаточно, чтобы это было выполнено для одной точки и одной прямой). Начало Л. г. было положено Н. И. Лобачевским , который впервые сообщил о ней в 1826. Несколько позднее эту же теорию предложил Я. Больяй ; поэтому Л. г. иногда называют геометрией Лобачевского – Больяя. Её также называют неевклидовой геометрией, хотя обычно термину «неевклидова геометрия» придают более широкий смысл, включая сюда и др. теории, возникшие вслед за Л. г., а также теории, основанные на изменении посылок евклидовой геометрии. Л. г. иногда называют гиперболич. неевклидовой геометрией в противоположность эллиптич. геометрии Римана (см. Неевклидовы геометрии , Римана геометрия ).

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Модели геометрии Лобачевского

Видео:1. Лобачевский и его наследие. Основные постулаты геометрии.Скачать

Задача

Геометрия Лобачевского — это такая геометрия, в которой не выполняется пятый постулат Евклида, аксиома параллельных. Вместо него принимается, что существует бесконечно много прямых, проходящих через не лежащую на прямой l точку и не пересекающих l. Геометрию Лобачевского можно реализовать на обычной евклидовой плоскости.

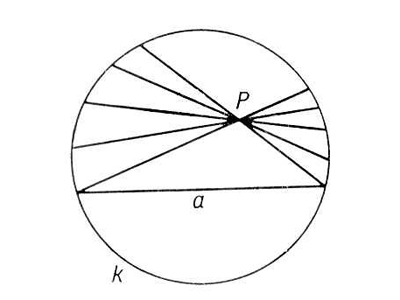
Примером служит модель Пуанкаре в круге. «Плоскостью» в этой модели называется внутренность обычного круга радиуса 1, а «прямыми» — дуги окружностей, перпендикулярных границе этого круга (окружности называются перпендикулярными, если перпендикулярны их касательные в точках пересечения). Граница круга называется абсолютом и считается не принадлежащей плоскости. Легко видеть, что через точку A, не лежащую на прямой l, действительно можно провести множество прямых, не пересекающих l. Все они находятся внутри угла, образованного прямыми a и b. Параллельными в смысле Лобачевского называются прямые, имеющие общую точку на абсолюте. Например, прямые l и a параллельны между собой. Прямые l и b тоже параллельны между собой (но при этом прямые a и b не параллельны).

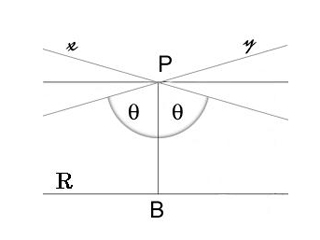
Между точками плоскости Лобачевского можно вычислить расстояние. Если Q, R — точки на плоскости, а P, S — точки, в которых прямая, проходящая через Q и R, пересекает абсолют, то расстояние на плоскости Лобачевского между Q и R равно

где PR и т. д. — обычные расстояния между двумя точками.

Впрочем, эта страшная формула для решения задачи не понадобится. Однако важно представлять себе в общих чертах, как устроены расстояния в геометрии Лобачевского. Параллельные прямые, как хорошо видно на рисунке, бесконечно сближаются друг с другом с одного конца и бесконечно отдаляются с другого. Если же прямые не пересекаются и не параллельны, то точки, двигающиеся по этим прямым к абсолюту, всегда бесконечно отдаляются друг от друга. Вообще, при приближении к абсолюту точка бесконечно удаляется от центра круга.

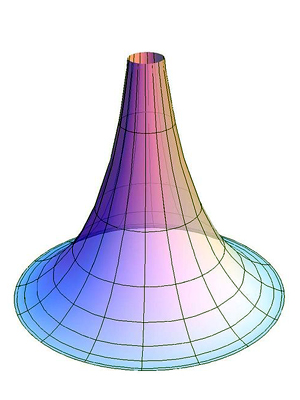
Другая реализация геометрии Лобачевского возможна на специальной поверхности в трехмерном пространстве — псевдосфере. Псевдосфера — поверхность вращения кривой ( z = ln left( text,frac t2 right) + cos t ), ( x = sin t ) вокруг оси Oz (впрочем, эта формула тоже не понадобится, нужно лишь представлять, что псевдосфера похожа на граммофонную трубу). Прямыми Лобачевского на этой поверхности являются геодезические, то есть линии кратчайшей длины, соединяющие две точки. Геодезическую можно получить, натянув по поверхности нить. Большая часть геодезических на псевдосфере — это спирали, навивающиеся на граммофонную трубу. Но геодезическими также являются сечения псевдосферы плоскостями, проходящими через ее ось вращения. Расстояния в этой модели — обычные евклидовы длины геодезических (поскольку псевдосфера вложена в обычное трехмерное пространство, то эти длины можно найти).

Псевдосфера, однако, не находится в однозначном соответствии со всей плоскостью Лобачевского в модели Пуанкаре. Во-первых, у псевдосферы есть граница, проходящая по плоскости z = 0. Во-вторых, у псевдосферы не такая топология, как у плоскости Лобачевского в модели Пуанкаре. Чтобы пояснить это утверждение, рассмотрим замкнутую кривую, делающую один оборот по псевдосфере вокруг оси Oz. Ясно, что никакими деформациями эта кривая не может быть стянута в точку: что бы мы ни делали, кривая всегда будет делать один оборот вокруг Oz (то есть кривую можно как угодно двигать по псевдосфере, можно изгибать ее, но нельзя допускать разрывов). Однако в модели Пуанкаре любая замкнутая кривая может быть непрерывно деформирована в точку! Разгадка состоит в том, что геометрия на псевдосфере лишь локально реализует геометрию Лобачевского. Это значит, что если вырезать кусок псевдосферы, в котором не будет отверстий, то ему можно будет однозначно сопоставить кусок плоскости Лобачевского из модели Пуанкаре, причем расстояние Лобачевского между любыми точками будет сохраняться. (Между евклидовой плоскостью и плоскостью Лобачевского нельзя построить даже локального соответствия, сохраняющего расстояния.)

Таким образом, псевдосфера состоит из кусков плоскости Лобачевского, гладко переходящих друг в друга. Как выполнить явное построение псевдосферы на основе модели Пуанкаре в круге? Другими словами, как склеить псевдосферу из одной или нескольких областей плоскости Лобачевского?

Видео:Уравнение прямой.Скачать

Подсказка 1

Конус и цилиндр — поверхности, на которых локально реализуется евклидова геометрия. Однако, разумеется, ни конус, ни цилиндр не являются целой евклидовой плоскостью. Как, имея в распоряжении лист бумаги (евклидову плоскость), построить цилиндр или конус?

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Подсказка 2

Как уже было сказано, сечения псевдосферы плоскостями, проходящими через ее ось симметрии, являются геодезическими, то есть прямыми. Обратите внимание: во-первых, псевдосфера бесконечна вверх. Во-вторых, она бесконечно сужается при движении вдоль оси симметрии. Это значит, что все прямые, о которых говорилось двумя строками выше, бесконечно сближаются (но не пересекаются), то есть параллельны. На псевдосфере, таким образом, есть целое семейство параллельных прямых.

Видео:УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Решение

Оказывается, что псевдосфера — аналог конуса, склеенного из евклидовой плоскости. Она получается из области, лежащей между двумя параллельными в смысле Лобачевского прямыми, склеиванием по этим прямым. Действительно, разрежем псевдосферу плоскостью, проходящей через ее ось симметрии. Тогда у каждой из полученных частей границами являются пары прямых, которые, как уже было отмечено в подсказке, параллельны. Если же сделать не два разреза, а один, то получится всего одна область, ограниченная двумя параллельными «лучами» Лобачевского a, b и кривой c, которая в трехмерном пространстве является окружностью. Эта область является разверткой псевдосферы; точно так же как сектор окружности в евклидовой плоскости — развертка конуса.

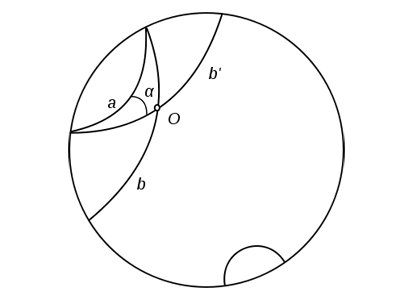
Рис. 3. На обоих рисунках серым цветом выделена одна и та же область плоскости Лобачевского. Слева она изображена в модели Пуанкаре, справа она вложена в трехмерное пространство. Область ограничена линиями a, b и c. a и b — лучи Лобачевского, перпендикулярные c, а c — отрезок орицикла. В модели Пуанкаре орицикл является окружностью, которая касается абсолюта

Из симметрии очевидно, что c перпендикулярна всему семейству параллельных прямых на псевдосфере. Кривая, обладающая таким свойством, носит в геометрии Лобачевского специальное название: орицикл. Чем же орицикл является в модели Пуанкаре? В евклидовой геометрии, разумеется, семейству параллельных прямых перпендикулярно другое семейство параллельных прямых. В геометрии Лобачевского это не так: кривая c, конечно, прямой не является. Впрочем, не составляет труда выяснить вид c в модели Пуанкаре. В этом помогает замечательный факт: евклидовы углы в модели Пуанкаре совпадают с углами плоскости Лобачевского. Поэтому задача сводится к следующей: найти кривую, перпендикулярную семейству касающихся друг друга в одной точке окружностей. У этой кривой нужно будет выбрать отрезок, равный по длине окружности основания псевдосферы.

Такой кривой является любая окружность, перпендикулярная общей касательной семейства и проходящая через точку касания. Отсюда немедленно следует, что эта окружность будет касаться абсолюта.

Таким образом, орицикл в модели Пуанкаре — любая окружность, касающаяся абсолюта, а развертка псевдосферы состоит из двух лучей и части орицикла. В некотором смысле это — «треугольник» с двумя прямыми углами. Следует подчеркнуть: пара «лучей» и отрезок могут быть выбраны произвольным образом, с условием, что лучи параллельны (в смысле Лобачевского) друг другу, перпендикулярны отрезку, а отрезок имеет заданную длину, а именно — 2π.

Интересно посмотреть, что будет, если отрезок c имеет длину, отличную от длины окружности в основании псевдосферы. В модели Пуанкаре это может соответствовать тому, что вместо b берется какая-нибудь другая прямая, параллельная а (например, одна из черных внутри серой области в левой части рис. 3).

Для понимания этого полезен тот факт, что плоскость Лобачевского однородна и изотропна. Из этого немедленно следует, что любую вырезанную часть псевдосферы можно, изгибая, свободно двигать по псевдосфере (возможно, с наложениями). Вырежем наш «прямоугольный треугольник» с конечным отрезком длины, меньшей 2π. Его можно двигать по псевдосфере вверх до тех пор, пока отрезок орицикла не сомкнется в окружность, а две границы не сольются. Таким образом, из такого треугольника получается псевдосфера, у которой отрезана нижняя часть.

Если же длина с больше 2π, то построить из такого треугольника фигуру вращения в евклидовом пространстве нельзя. Однако его можно разрезать на треугольники, у каждого из которых сторона будет меньше 2π, каждый из них разместить на псевдосфере и склеить между собой. Таким образом, треугольник будет «намотан» на псевдосферу. Наконец, саму псевдосферу можно склеить не из одного треугольника, а из нескольких (подумайте, как).

Видео:УРАВНЕНИЕ ПРЯМОЙСкачать

Послесловие

Кроме модели Пуанкаре и псевдосферы существуют и другие модели геометрии Лобачевского. Исторически первой появилась модель Клейна в круге. В ней прямыми называются не дуги окружностей, а хорды, а расстояние вычисляется по точно такой же формуле. Другая модель — тоже Пуанкаре, но в полуплоскости. Ее можно представлять себе как модель Пуанкаре, у которой радиус круга устремлен к бесконечности. Абсолют превращается в границу полуплоскости, прямые Лобачевского — в полуокружности, перпендикулярные абсолюту, либо в прямые, перпендикулярные абсолюту.

Попробуем взглянуть единым взглядом на все эти модели. Каждая модель состоит из нескольких обязательных «ингредиентов». Необходимо определить, во-первых, что такое сама плоскость Лобачевского. Это всегда некоторая двумерная поверхность, возможно вложенная в объемлющее пространство (как псевдосфера). Во-вторых — что такое прямые на этой плоскости Лобачевского. Это некоторые кривые на поверхности (мы каждый раз указывали, какие именно кривые принимаются за «прямые» в разных моделях). И, наконец, всегда должен быть какой-то способ определять расстояния на этой плоскости (так называемая метрика), причем так, чтобы прямая всегда была кратчайшим путем между двумя точками.

Нетрудно заметить, что эти «ингредиенты» немного избыточны в том смысле, что необходимо проверить, что прямая — действительно кратчайшее расстояние между двумя точками. Это вовсе не очевидно для формулы из условия:

Чтобы избавиться от этой избыточности, можно определять геометрию немного по-другому. А именно, будем задавать расстояния не между какими угодно двумя точками, а только между бесконечно близкими. После этого можно естественным образом определить длину кривой, разбив ее на малые части и просуммировав их длины (то есть взяв интеграл по кривой). Наконец, назовем отрезком прямой в этой геометрии линию, соединяющую две точки и имеющую кратчайшую длину.

Метрика полностью определяет внутренние свойства поверхности, в частности, насколько и каким образом эта поверхность искривлена. Таким образом, мы пришли к тому, с чего начали: геометрия Лобачевского — это геометрия искривленной поверхности, а именно — псевдосферы. А все модели геометрии Лобачевского — это разные системы координат, введенные на плоскости Лобачевского. Метрики моделей, разумеется, отличаются между собой, но при этом описывают одну и ту же геометрию.

Чтобы не быть голословными, выпишем явно метрики для евклидового пространства и геометрии Лобачевского. Начнем с модели Пуанкаре в верхней полуплоскости, потому что в ней сразу будут видны все особенности, характерные для искривленных поверхностей. Пусть две точки имеют координаты (x, y) и (x + dx, y + dy). Тогда квадрат расстояния между ними вычисляется по формуле

Для евклидовой плоскости вместо этого есть всем известная формула

[ mathrms^2 = mathrmx^2 + mathrmy^2, ]

которая есть не что иное, как теорема Пифагора.

Метрики для модели Клейна и Пуанкаре можно при желании посмотреть, например, в Википедии (см. Beltrami–Klein model и Poincaré disk model).

Еще более глубокое изучение вопроса приведет нас к такому понятию, как кривизна пространства. Не вдаваясь в подробности, обратим внимание лишь на то, что поверхность может быть искривлена в каждой точке двумя качественно различными способами. В одном случае поверхность напоминает часть эллипсоида, и кривизна считается положительной. В другом случае поверхность похожа на седло, и ее кривизна отрицательна. Псевдосфера, как видно на ее изображении (а значит, и плоскость Лобачевского), имеет отрицательную кривизну, причем оказывается, что эта кривизна постоянна (не зависит от точки поверхности). Это, кстати, проясняет происхождение названия «псевдосфера»: обычная сфера является поверхностью с постоянной положительной кривизной.

Рис. 4. Слева направо: поверхность отрицательной кривизны (однополостный гиперболоид), поверхность нулевой кривизны (цилиндр) и поверхность положительной кривизны (сфера). Рисунок с сайта en.wikipedia.org

Геометрия Лобачевского, созданная в XIX веке, была важнейшей ступенью к созданию области математики, которая сейчас называется дифференциальной геометрией. Она занимается изучением произвольных искривленных пространств, а ее математический аппарат является фундаментом такой важной области современной физики, как общая теория относительности (ОТО). Дело в том, что, согласно ОТО, пространство-время, в котором мы живем, обладает кривизной, причем кривизна пространства соответствует наличию в этой точке пространства гравитационного поля.

ОТО подверглась многочисленным экспериментальным проверкам (см.: Столетие ОТО, или Юбилей Первой ноябрьской революции, «Элементы», 25.11.2015), а поправки, связанные с ней, приходится учитывать для точной спутниковой навигации. Кроме того, ей описывается физика массивных объектов, таких как обычные и нейтронные звезды, сверхновые и черные дыры (список можно продолжать). Наконец, ОТО лежит в основе современной науки о Вселенной — космологии.

Согласно здравому смыслу, а также всем имеющимся наблюдательным данным, Вселенная на больших масштабах однородна и изотропна. Это в любом случае означает, что она является пространством постоянной пространственной кривизны. В связи с этим с самых первых лет космологии рассматривались три возможности: плоская Вселенная, Вселенная положительной кривизны («сферическая Вселенная») и Вселенная отрицательной кривизны («Вселенная Лобачевского»). На данный момент, правда, считается, что кривизна Вселенной нулевая (в пределах современной точности измерений). Это находит объяснение в современной теории инфляции. Согласно последней, Вселенная в начальной стадии своей эволюции испытывала очень быстрое расширение и в результате увеличилась во много раз (это и называется инфляцией). Вполне возможно, что до инфляции Вселенная была сферической, «Вселенной Лобачевского» или имела какую-то другую сложную геометрию. Однако расширение привело к тому, что сейчас наблюдениям доступна лишь очень малая часть всей Вселенной, и ее геометрия должна быть неотличима от плоской.