 Линейная функция Линейная функция |
 График линейной функции График линейной функции |
 Прямые, параллельные оси ординат Прямые, параллельные оси ординат |
 Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые |
- Линейная функция
- График линейной функции
- Прямые, параллельные оси ординат
- Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
- Общее уравнение прямой на плоскости. Неполные уравнения прямой
- Геометрия Расположение прямой относительно системы координат. — презентация
- Похожие презентации
- Презентация на тему: » Геометрия Расположение прямой относительно системы координат.» — Транскрипт:
- 🎥 Видео
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Линейная функция
Линейной функцией называют функцию, заданную формулой
| y = kx + b, | (1) |
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия .
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .
Видео:Уравнение прямой. Видеоурок 6. Геометрия 9 классСкачать

График линейной функции
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.
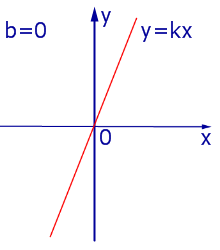 |
| Рис.1 |
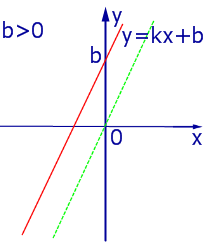 |
| Рис.2 |
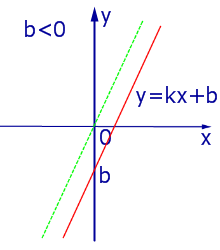 |
| Рис.3 |
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
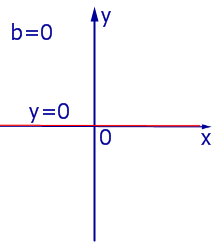 |
| Рис.4 |
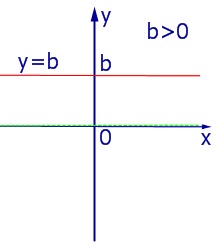 |
| Рис.5 |
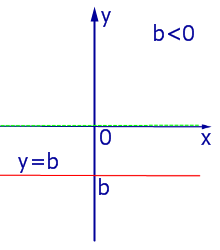 |
| Рис.6 |
При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.
| k y = kx + b1 и y = kx + b2 , имеющие одинаковые угловые коэффициенты и разные свободные члены имеющие разные угловые коэффициенты y = kx + b1 и перпендикулярны при любых значениях свободных членов. Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b . При Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать  Прямые, параллельные оси ординатПрямые, параллельные оси Oy , задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .; Видео:9 класс, 7 урок, Уравнение прямойСкачать  Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
где p, q, r – произвольные числа. В случае, когда что и требовалось. В случае, когда откуда вытекает, что уравнение (4) задает прямую линию вида (3). В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости: В случае, когда Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4) . Замечание 3 . При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4) . Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство Итак, уравнение прямой, параллельной к прямой В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство Видео:Составляем уравнение прямой по точкамСкачать  Общее уравнение прямой на плоскости. Неполные уравнения прямойОбщее уравнение прямой: Ax + By + C = 0. Этим уравнением можно задать любую прямую. Коэффициенты А, В, С при этом определяются не однозначно, а с точностью до пропорциональности. Уравнение Ax + By + C = 0 называется неполным уравнением прямой на плоскости, если хотя бы один из его коэффициентов А, В, С равен нулю. Если коэффициент B = 0, A ≠ 0 ≠ C , то из уравнения Ax + By + C = 0 следует x = — C / A = a. Это уравнение прямой, параллельной оси Оу, отсекающей от оси Ох отрезок величиной а. Если коэффициент A = 0, B ≠ 0 ≠ C то из уравнения Ax + By + C = 0 следует y = — C / B = b. Это уравнение прямой, параллельной оси Ох, отсекающей от оси Оу отрезок величиной b. Если C = 0, то уравнение Ax + By + C = 0 принимает вид Ax + By = 0. Ясно, что эта прямая проходит через начало координат. Если в уравнении Ax + By = 0 коэффициент B ≠ 0 , то отсюда получаем y = — k = — Если в уравнении Ax + By = 0 A ≠ B = 0, то Ax = 0 и, сокращая на А, получаем уравнение оси Оу: x = 0. Если в уравнении Ax + By = 0 B ≠ A = 0, то By = 0 и, сокращая на В, получаем уравнение оси Ох: y = 0. Подведем итог исследования общего уравнения прямой Ax + By + C = 0: 1) Если A ≠ 0, B ≠ 0, C ≠ 0 , то уравнение Ax + By + C = 0 может быть записано в виде уравнения прямой в отрезках: x /a + y / b = 1 – прямая, отсекающая от осей координат отрезки величиной а и b соответственно. 2) Если A = 0, B ≠ 0, C ≠ 0, то уравнение может быть записано в виде: y = b – прямая параллельная оси Ох и отсекающая от оси Оу отрезок величины b. 3) Если A ≠ 0, B = 0, C ≠ 0, то уравнение может быть записано в виде: x = a – прямая параллельная оси Оу и отсекающая от оси Ох отрезок величины а. 4) Если A = 0, B ≠ 0, C = 0, то уравнение прямой имеет вид: y = 0 – прямая совпадает с осью Ох. 5) Если A ≠ 0, B = 0, C = 0, то уравнение прямой имеет вид: x = 0 – прямая совпадает с осью Оу. 6) Если A ≠ 0, B ≠ 0, C = 0, то уравнение может быть записано в виде: y = k * x – уравнение прямой с угловым коэффициентом. 17. Общее уравнение прямой на плоскости. Уравнение прямой в «отрезках» (с выводом) Общее уравнение прямой: Ax + By + C = 0. Этим уравнением можно задать любую прямую. Коэффициенты А, В, С при этом определяются не однозначно, а с точностью до пропорциональности. Уравнение прямой в отрезках: Пусть ни один из коэффициентов А, В, С общего уравнения прямой Ax + By + C = 0, не равен нулю. Перенесем свободный член С в правую часть уравнения и разделим обе части уравнения на (– С): Обозначим Для построения прямой достаточно взять две точки на этой прямой. Для построения прямой в отрезках удобно найти ее точки пересечения с координатными осями: М(а, 0) – точка пересечения прямой : N(0, b) – точка пересечения прямой : Говорят, что прямая отсекает от координатных осей отрезки ОМ и ОN величина которых равна числам а и b соответственно. Под величиной отрезка ОА здесь понимается не его длина Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать  Геометрия Расположение прямой относительно системы координат. — презентацияПрезентация была опубликована 8 лет назад пользователемhot.ee Похожие презентацииВидео:Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать  Презентация на тему: » Геометрия Расположение прямой относительно системы координат.» — Транскрипт:1 Геометрия Расположение прямой относительно системы координат 2 Каноническое уравнение прямой Ax + By + C = 0 Рассмотрим, как расположена прямая относительно осей координат, если её уравнение имеет тот или иной частный вид. 3 1. А=0, В0 В этом случае уравнение прямой : Ву + С = 0 или Все точки прямой имеют одну и туже ординату (-С/В) Следовательно прямая параллельна оси Ох Если С = 0, то прямая совпадает с осью Ох 4 2. В = 0, А 0 В этом случае уравнение выглядит так : Ах + С = 0 или Прямая параллельна оси Оу Если С= 0, то она совпадает с осью Оу 5 3. С= 0 Уравнение приняло вид Ах + Ву = 0 В этом случае прямая проходит через начало координат, т.к. Координаты (0;0) удовлетворяют уравнение прямой 6 Геометрический смысл коэффициента k Если в общем уравнении прямой Ах + Ву+ С = 0 коэффициент при у не равен нулю т.е. В0, то уравнение можно разрешить относительно у. Получим: Обозначая = g, = k, Получим у = kх + g 7 Геометрический смысл коэффициента k Выясним геометрический смысл коеффициента в этом уравнении. Возьмём две точки на прямой А (х1;у1),В(х2;у2) причём х1 8 Геометрический смысл коэффициента k 9 Геометрический смысл коэффициента k В случае, представленном на рис.1, В случае, представленном на рис.2, Таким образом, коэффициент в уравнении прямой равен тангенсу острого угла, который образует прямая с осью Ох. Коэффициент k в уравнении прямой называют угловым коэффициентом прямой 10 конец Составили урок: Наталья Кобелева Мосягина Марина Юхкам Антонина Крылова Елена 🎥 ВидеоМатематика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать  Уравнение прямой по двум точкамСкачать  Угловой коэффициент прямойСкачать  Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  Уравнение параллельной прямойСкачать  11. Прямая в пространстве и ее уравненияСкачать  №972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать  12. Уравнения прямой в пространстве Решение задачСкачать  Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать  §9 Уравнение прямой в отрезкахСкачать 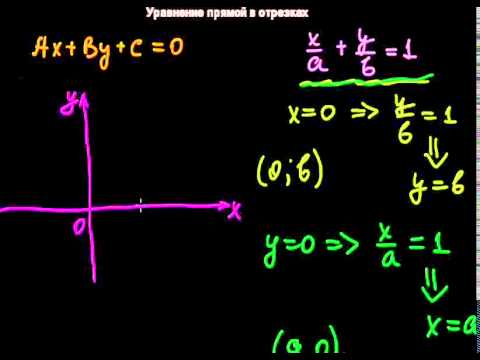 Математика без Ху!ни. Уравнение плоскости.Скачать  УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать  |

 , параллельны .
, параллельны . , пересекаются при любых значениях свободных членов.
, пересекаются при любых значениях свободных членов.



 прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле
прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле



 уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .
уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .

 получаем:
получаем:

 уравнение (5) решений вообще не имеет.
уравнение (5) решений вообще не имеет.
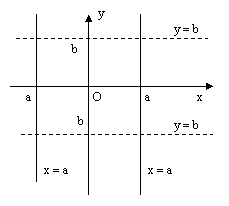
 x. Обозначив через
x. Обозначив через +
+  = 1.Здесь знаменатели а и b – это координаты точек пересечения прямой с соответствующими координатными осями. С помощью такого уравнения невозможно задать прямую, проходящую через начало координат или параллельную одной из осей.
= 1.Здесь знаменатели а и b – это координаты точек пересечения прямой с соответствующими координатными осями. С помощью такого уравнения невозможно задать прямую, проходящую через начало координат или параллельную одной из осей.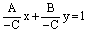 .
. . Тогда последнее уравнение можно записать в виде: :
. Тогда последнее уравнение можно записать в виде: : 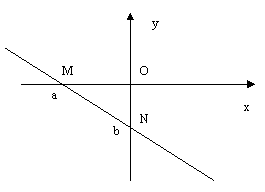
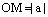 , а координата точки М, т.е. число а. Аналогично, величина отрезка ОN равна числу b.
, а координата точки М, т.е. число а. Аналогично, величина отрезка ОN равна числу b.