Уравнение прямой с угловым коэффициентом и начальной ординатой

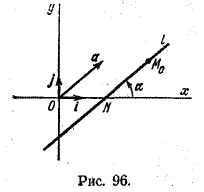
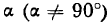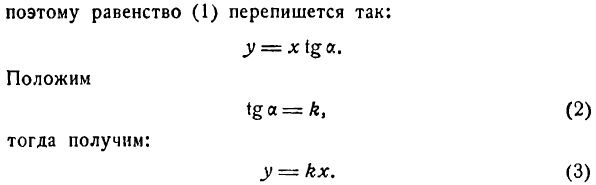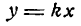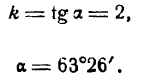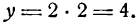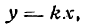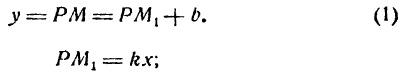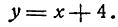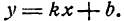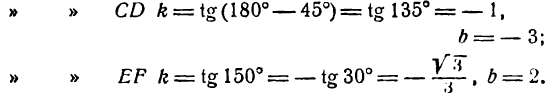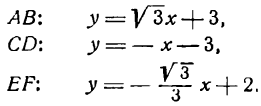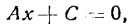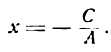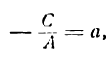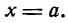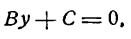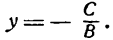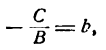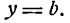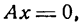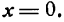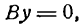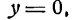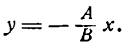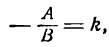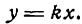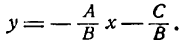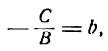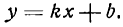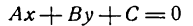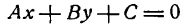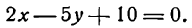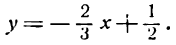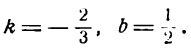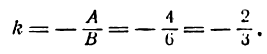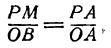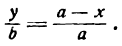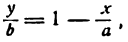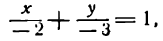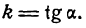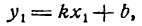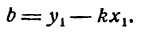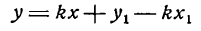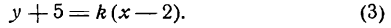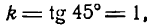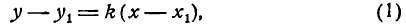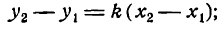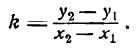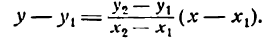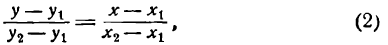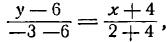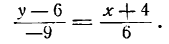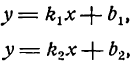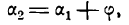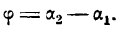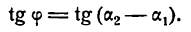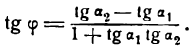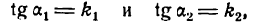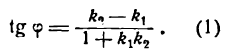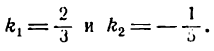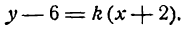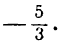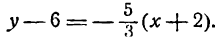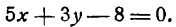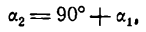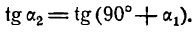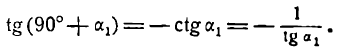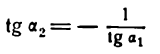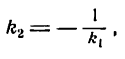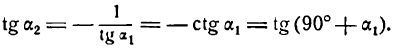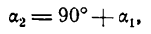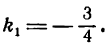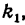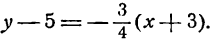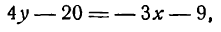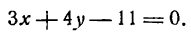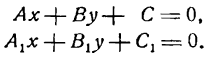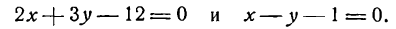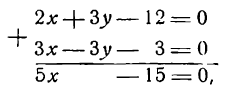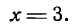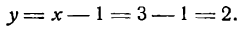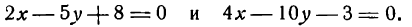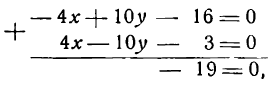Пусть на плоскости, где имеется прямоугольная декартова система координат, прямая l проходит через точку М₀ параллельно направляющему вектору а (рис. 96).

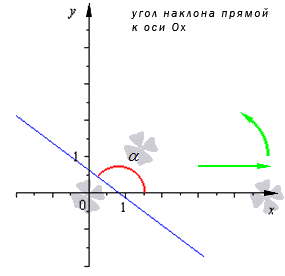
Если прямая l пересекает ось Ох (в точке N), то под углом прямой l с осью Ох будем понимать угол α, на который необходимо повернуть ось Ох вокруг точки N в направлении, обратном вращению часовой стрелки, чтобы ось Ох совпала с прямой l. (Имеется в виду угол, меньший 180°.)

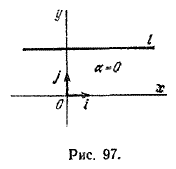
Этот угол называют углом наклона прямой. Если прямая l параллельна оси Ох, то угол наклона принимается равным нулю (рис. 97).

Тангенс угла наклона прямой называется угловым коэффициентом прямой и обычно обозначается буквой k:

Если α = 0, то и k = 0; это означает, что прямая параллельна оси Ох и ее угловой коэффициент равен нулю.

Если α = 90°, то k = tg α не имеет смысла: это означает, что прямая, перпендикулярная оси Ох (т. е. параллельная оси Оу), не имеет углового коэффициента.

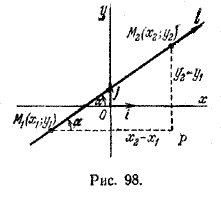
Угловой коэффициент прямой можно вычислить, если известны координаты двух каких-либо точек этой прямой. Пусть даны две точки прямой: M₁(x₁; у₁) и M₂(x₂; у₂) и пусть, например, 0 x₁, у₂ > у₁ (рис. 98).

Тогда из прямоугольного треугольника M₁РM₂ находим

Аналогично доказывается, что формула (2) верна и в случае 90° 3 х + 3у — 7 = 0.

Приведем данное уравнение к виду

Следовательно, k = tg α = — 1 /_{√ 3} , откуда α = 150°

Задача 5. Составить уравнение прямой, проходящей через точку Р(3; -4), с угловым коэффициентом k = 2 /₅

Задача 6. Составить уравнение прямой, проходящей через точку Q (-3; 4) и составляющей с положительным направлением оси Ох угол 30°.

Если α = 30°, то k = tg 30° = √ 3 /₃. Подставив в уравнение (4) значения x₁, y₁ и k, получим

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Прямая линия в математике с примерами решения и образцами выполнения

Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).

Видео:Угловой коэффициент прямойСкачать

Уравнения прямых, параллельных осям координат

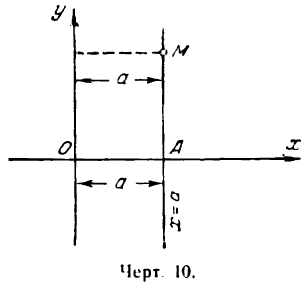
Возьмем прямую линию, параллельную оси Оу и проходящую на расстоянии а от нее (рис. 10).

Все точки этой прямой одинаково удалены от оси ординат на расстояние, равное а. Следовательно, для каждой точки прямой АМ абсцисса одна и та же, а именно:

х = а, (1)

ордината же различна. Таким образом, уравнение (1) вполне определяет прямую, параллельную оси Оу, а потому оно является ее уравнением. Возьмем прямую, параллельную оси Ох, на расстоянии.

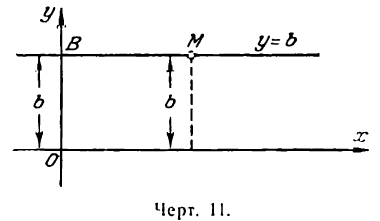
равном b от нее (рис. 11). Все точки этой прямой одинаково удалены от оси Ох на расстояние, равное b , т. е. любая точка прямой ВМ имеет постоянную ординату, а именно:

абсциссу же различную. Как видно, уравнение (2) вполне определяет прямую, параллельную оси Ох, а потому оно является ее уравнением.

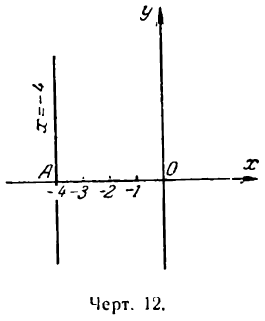
По уравнениям (1) и (2) можно построить соответствующие им прямые. Пусть, например, дана прямая х = — 4. Отложив на оси Ох отрезок ОА = — 4 (рис. 12) и проведя через точку А прямую, параллельную оси Оу, получим искомую прямую.

Уравнения осей координат

Возьмем уравнение прямой, параллельной оси Оу:

х = а

и станем в нем уменьшать абсолютную величину а, тогда прямая, определяемая этим уравнением, будет приближаться к оси Оу, оставаясь все время ей параллельной, и при а = 0 сольется с ней. Уравнение х = 0 является уравнением оси Оу.

Если же в уравнении у = b прямой, параллельной оси Ох, будем уменьшать абсолютную величину b то эта прямая станет приближаться к оси Ох, оставаясь ей параллельной, и при b = 0 с ней совпадет. Таким образом, уравнение у = 0 будет уравнением оси Ох.

Уравнение прямой, проходящей через начало координат

Проведем прямую через начало координат под углом

к оси Ох (рис. 13). Принято положительный угол а отсчитывать от положительного направления оси абсцисс в сторону, противоположную движению часовой стрелки (рис. 13), а отрицательный — по часовой стрелке.

Возьмем на проведенной прямой произвольную точку М (х; у). Опустив перпендикуляр МР на ось Ох, получим прямоугольный треугольник ОМР, из которого найдем:

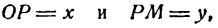
Координаты любой точки прямой ОМ удовлетворяют полученному уравнению; можно показать, что координаты любой точки, не лежащей на прямой ОМ, не удовлетворяют ему; поэтому оно является уравнением прямой ОМ. Итак,

есть уравнение прямой, проходящей через начало координат. В нем х и у — текущие координаты, а — угловой коэффициент.

Определение:

Угловым коэффициентом прямой называется тангенс угла наклона этой прямой к положительному направлению оси Ох.

Величина может быть как положительной, так и отрицательной. Если угол а острый, то тангенс его имеет положительное значение; если же угол а тупой, —то отрицательное. Поэтому величина в уравнении прямой будет положительной, если а — острый угол, и отрицательной, если тупой.

Заметим, что при а = 90° углового коэффициента не существует, так как 90° не имеет числового значения.

Зная угловой коэффициент прямой у = х, можно определить ее положение.

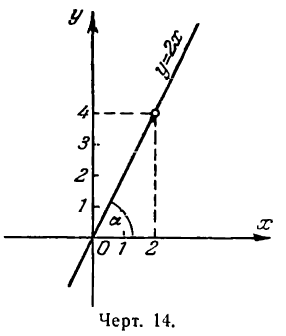
Пусть требуется построить прямую у= 2х.

Для этого найдем угол а из условия

Построив при точке О найденный угол, мы и получим искомую прямую (рис. 14).

Построение этой прямой можно провести и проще.

Известно, что положение прямой определяется двумя точками, поэтому для решения задачи нужно знать их координаты. В нашем же случае достаточно определить координаты одной точки, так как вторая (начало координат) нам известна. Для этого дадим х произвольное значение, например х = 2, тогда из уравнения прямой найдем:

Значения х = 2 и у = 4 и будут координатами точки, лежащей на данной прямой. Построив эту точку, проведем через нее и начало координат прямую линию (рис. 14).

Уравнение прямой с угловым коэффициентом и начальной ординатой

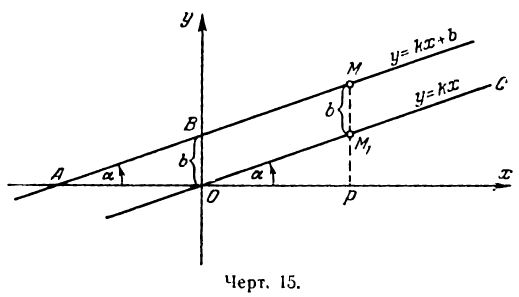
Пусть дана прямая ОС, проходящая через начало координат под углом а к положительному направлению оси Ох (рис. 15)

Ее уравнение имеет вид

где .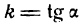

Проведем прямую 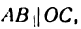отсекающую на оси Оу отрезок ОВ = b. Прямая АВ составляет с положительным направлением оси Ох тот же угол а. Пусть М(х; у)— произвольная точка прямой АВ. Из рис. 15 найдем:

Подставив значение РМ1 в равенство (1), получим уравнение прямой АВ в виде:

где — угловой коэффициент, а b называется начальной ординатой.

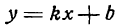
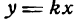
Заметим что прямая получается смещением всех точек прямой (рис. 15) на отрезок b вверх (при положительном b) и вниз при отрицательном b .

Уравнение 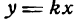определяющее прямую проходящую через начало координат, является частным случаем уравнения (2) при b = 0.

Зная угловой коэффициент и начальную ординату b можно определить положение прямой. Пусть, например, требуется построить прямую

Из данного уравнения имеем:

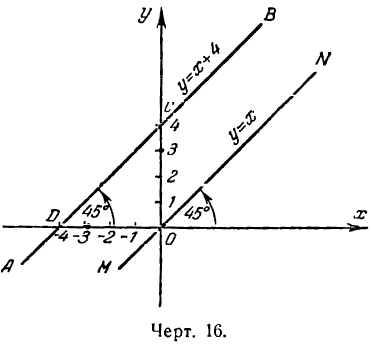
Проведем через начало координат прямую МN под углом в 45 градусов к положительному направлению оси Ох (рис. 16). На прямую

Как видно из уравнения ее пересекает ось Оу на расстоянии ОС, равном 4 единицам масштаба от начала координат.

Поэтому прямая АВ, проведенная через точку С параллельно прямой МN, и будет искомой.

Однако проще построить указанную прямую по двум ее точкам. Удобнее для этого брать точки пересечения прямой с осями координат. Одна из них — точка С пересечения прямой с осью Оу— дается самим уравнением, а именно С(0; 4). Для нахождения точки D пересечения этой прямой с осью Ох положим в данном уравнении y = 0, получим х = — 4; значит, прямая пересекает ось Ох в точке D (-4; 0). Строим точки С и D и проводим через них искомую прямую.

Пример:

Найти уравнения прямых АВ, СD и ЕF, изображенных на рис. 17.

Решение:

Чтобы написать уравнения данных прямых, нужно определить величины и b, а затем подставить их значения в уравнение

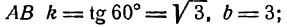
Следовательно, уравнения данных прямых будут:

Общее уравнение прямой

В предыдущей лекции были выведены следующие виды уравнения прямой: уравнение прямой, параллельной оси Оу:

уравнение прямой, параллельной оси Ох:

уравнение оси Оу:

уравнение оси Ох:

уравнение прямой, проходящей через начало координат:

уравнение прямой с угловым коэффициентом и начальной ординатой:

Уравнения (1) — (6) исчерпывают все возможные положения прямой, поэтому можно сказать, что

всякая прямая линия определяется уравнением первой степени относительно текущих координат.

Покажем теперь, что указанные виды уравнения прямой можно получить из уравнения

при некоторых частных значениях коэффициентов А, В и С.

I. Если В = 0, то уравнение (7) обратится в следующее:

Уравнение 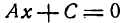есть уравнение прямой, параллельной оси Оу.

II. Если А = 0, то

Уравнение 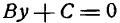определяет прямую, параллельную оси Ох.

III. Если В = 0 и С = 0, то

IV. Если А = 0 и С = 0, то

V. Если С = 0, то

Уравнение 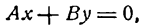определяет прямую, проходящую через начало координат.

VI. Если ни один из коэффициентов уравнения (7) не равен нулю, то и в этом случае его можно преобразовать в знакомую нам форму уравнения прямой. Найдем из уравнения (7) значение у:

включает в себя все рассмотренные нами ранее уравнения прямой; поэтому оно называется общим уравнением прямой. Итак, всякое уравнение первой степени

при любых значениях коэффициентов А, В и С, исключая одновременное равенство А и В нулю, определяет прямую линию.

Пример:

Построить прямую

Решение:

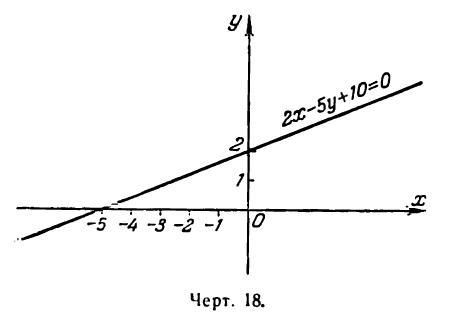
Проще всего построить прямую по двум ее точкам пересечения с осями координат. Положив в данном уравнении у = 0, получим х =- 5; координаты (-5; 0) и будут определять положение точки пересечения прямой с осью Ох. Для нахождения точки пересечения прямой с осью Оу положим в том же уравнении х = 0 тогда найдем у = 2; координаты искомой точки будут (0; 2).

Построив эти точки, проводим через них прямую 2х— 5у —10 = 0 (рис. 18).

Пример:

Найти угловой коэффициент и начальную ординату прямой 4х+ 6у — 3 = 0.

Решение:

Преобразуем это уравнение к виду

для этого находим:

6у = — 4х + 3,

Сравнив полученное уравнение с уравнением 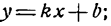найдем:

Угловой коэффициент можно найти и из равенства (8). Для этого, как видно, нужно коэффициент при х общего уравнения прямой разделить на коэффициент при у и частное

взять с противоположным знаком. Таким образом, в данном примере

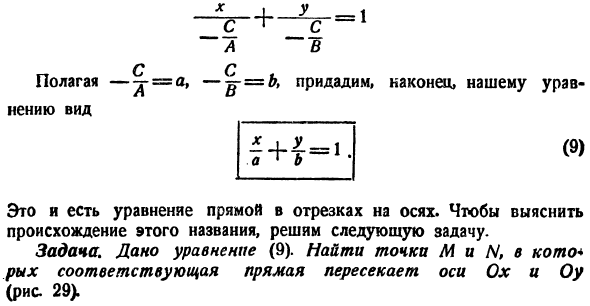
Уравнение прямой в отрезках

Как мы уже знаем, положение прямой определяется или двумя точками или одной точкой и углом наклона прямой к оси Ох. Если прямая не параллельна ни одной из координатных осей и не проходит

через начало координат, то ее положение может быть определено и другими данными, например отрезками, которые она отсекает на осях. Выведем уравнение прямой для этого случая.

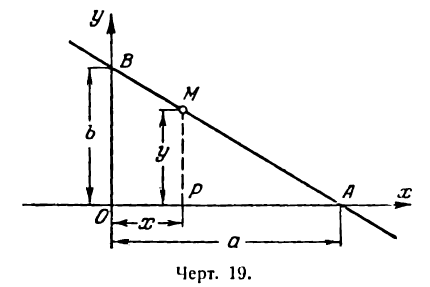
Пусть дана прямая, отсекающая на координатных осях отрезки ОА = а и ОВ = b (рис. 19).

Возьмем на этой прямой произвольную точку M (х; у) и проведем

МР 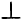Ох. Из подобия треугольников РМА и ОВА имеем:

Разделив а — х почленно на а, будем иметь:

Можно показать, что координаты любой точки нашей прямой будут удовлетворять этому равенству, а потому его нужно рассматривать как уравнение прямой АВ.

В уравнение (1) входят отрезки а и b , отсекаемые прямой на осях; поэтому оно называется уравнением прямой в отрезках.

Величины а и b могут быть как положительными, так и отрицательными в зависимости от того, в какую сторону от начала координат откладываются отрезки а и b .

Пусть, например, дана прямая АВ (рис. 20). Здесь а = — 2, b = — 3; следовательно, уравнение прямой АВ запишется в таком виде:

По уравнению вида (1) Очень просто строится прямая. Для этого нужно только отложить на осях отрезки а и b взятые из уравнения, и через их концы провести прямую.

Заметим, что уравнение в отрезках легко получается из общего уравнения прямой: Ах + Ву + С= 0, если все коэффициенты общего уравнения отличны от нуля (иначе уравнение в отрезках не имеет смысла).

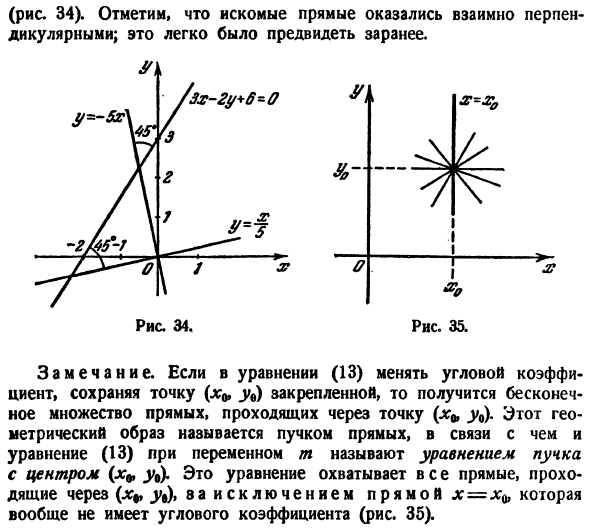
Уравнение пучка прямых

Пусть прямая АВ проходит через точку М(х1; у1) и образует угол а с положительным направлением оси Ох (рис. 21). Составим для прямой АВ уравнение вида

Для этого нужно найти величины и b определяющие прямую АВ, а затем подставить в уравнение (1) их значения. Так как угол а дан, то величина определится из равенства

Для нахождения b воспользуемся тем, что точка М лежит на прямой (1) и, следовательно, ее координаты удовлетворяют уравнению этой прямой.

Подставив в уравнение (1) вместо х и у их значения х1 и у1, а величину полагая известной, получим

Уравнение (1) можем теперь записать в виде

Таково искомое уравнение прямой АВ; в нем имеет одно, вполне определенное значение.

Допустим, что через ту же точку M(х1; у1) проходит несколько прямых; тогда угол а наклона этих прямых к оси Ох, и также множитель в уравнении (2) будут иметь различные значения.

В таком случае уравнение (2) будет определять уже не одну прямую, проходящую через данную точку M, а множество прямых, пересекающихся в эточке.

Совокупность всех прямых, проходящих через одну точку М, называется пучком прямых с центром в точке М. Таким образом, уравнение (2) с переменным можно рассматривать как уравнение пучка прямых, проходящих через данную точку, исключая прямую, параллельную оси ординат (так как tg 90° не имеет числового значения) (рис. 21).

Чтобы выделить из этого пучка прямую, образующую заданный угол с осью Ох, нужно в уравнении (2) вместо подставить его числовое значение. Пусть, например, пучок прямых проходит через точку М(2;—5), тогда его уравнение будет:

Выделим из этого пучка одну прямую, которая наклонена к положительному направлению оси Ох под углом а = 45°;

и уравнение (3) обратится в следующее:

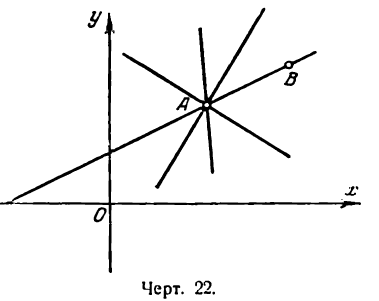
Уравнение прямой, проходящей через две данные точки

Пусть даны две точки A(х1; у1) и В(х2; у2); требуется найти уравнение прямой, проходящей через эти точки.

Если взять одну точку, например А, то через нее можно провести пучок прямых, уравнение которого будет:

где каждому значению отвечает одна прямая.

Выделим из этого пучка прямую, которая проходит и через вторую точку В (рис. 22). Чтобы найти ее уравнение, необходимо определить угловой коэффициент. Для этого примем во внимание, что точка В лежит на искомой прямой, и потому ее координаты должны обращать уравнение (1)

в тождество при равном угловому коэффициенту этой прямой. Подставив в уравнение (1) вместо текущих координат х и у координаты точки В, получим:

отсюда находим угловой коэффициент искомой прямой:

Уравнение (1) можно переписать так:

Преобразуем это уравнение, разделив обе части его на у2 — у1 получим:

гле х и у — текущие координаты. Равенство (2) является уравнением прямой, проходящей через две данные точки. Это, как и уравнение в отрезках, частный случай общего уравнения прямой.

Если х1 = х2 или у1 = у2, то формула (2) теряет смысл, так как делить на нуль нельзя. В этих случаях точки А и В лежат либо на прямой, параллельной оси Оу, либо на прямой, параллельной оси Ох. В первом случае уравнение прямой запишется в виде

х = х1

а во втором — в виде

Пример:

Написать уравнение прямой, проходящей через две точки: А(—4; 6) и В(2; —3).

Решение:

х1 = —- 4, х2 = 2

у1 = 6, у2 = — 3.

Подставим эти значения в уравнение (2); получим:

Умножив обе части последнего уравнения на —18, будем иметь:

2у— 12 = — 3х— 12,

Зх + 2у = 0.

Пример:

Через две точки А( 3; 2) и В (5; 2) проходит прямая. Написать ее уравнение.

Решение:

Так как ординаты данных точек равны, то заключаем, что искомая прямая параллельна оси Ох, а потому ее уравнение будет

Угол между двумя прямыми

Пусть даны уравнения двух прямых:

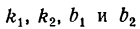
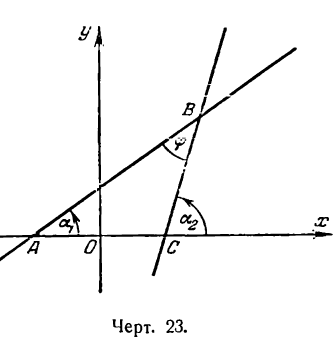
где имеют вполне определенные значения. Выведем формулу для определения угла между этими прямыми.

Обозначим углы, образуемые данными прямыми с положительным направлением оси Ох, через а1 и а2, а угол между этими прямыми через 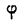(рис. 23).

Угол а2, как внешний угол треугольника ABC, будет равен сумме внутренних, с ним не смежных, т. е.

Если углы равны между собой, то и тангенсы их равны друг другу, поэтому

Применяя формулу для тангенса разности двух углов, получим:

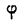
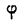
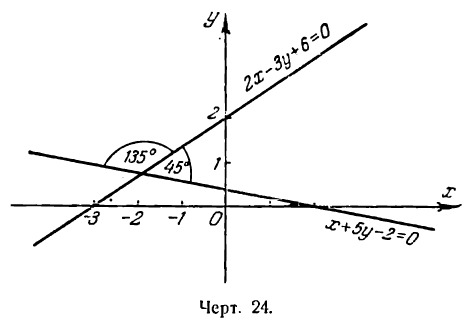
Определив tg по формуле (1), можно найти и самый угол .

Пример:

Определить угол между прямыми:

2х — 3у + 6 =0

х + 5у — 2=0.

Решение:

Из данных уравнений найдем угловые коэффициенты этих прямых :

Согласно формуле (1) имеем:

Полученный угол между прямыми тупой. Но если принять

то вычисляя 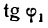по той же формуле (1), получим:

откуда 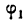= 45°. Получился угол острый, смежный с ранее

найденным тупым углом (рис. 24). Первое и второе значение угла будет ответом на вопрос задачи.

Условие параллельности прямых

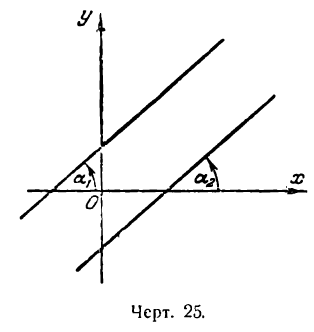
Если прямые параллельны между собой, то они образуют одинаковые углы а1 и а2 с положительным направлением оси Ох (рис. 25).

Из равенства углов а1 и а2 следует

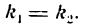
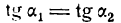
Обратно, если т.е. то а1 = а2, а это значит, что данные прямые параллельны.

Итак, если прямые параллельны между собой, то их угловые коэффициенты равны (и наоборот).

Пример:

Написать уравнение прямой, проходящей через точку А (—2; 6) и параллельной прямой 5х—3у — 7 = 0.

Решение:

Через точку А проходит пучок прямых, среди которых находится искомая прямая. Следовательно, прежде всего пишем уравнение пучка прямых , проходящих через точку А:

Затем находим из данного в задаче уравнения прямой ее угловой коэффициент; применяя равенство (8) , получим:

Согласно условию параллельности угловой коэффициент искомой прямой тоже равен

Подставим найденное значение 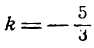в уравнение

Выполнив необходимые преобразования, получим искомое уравнение прямой:

Условие перпендикулярности прямых

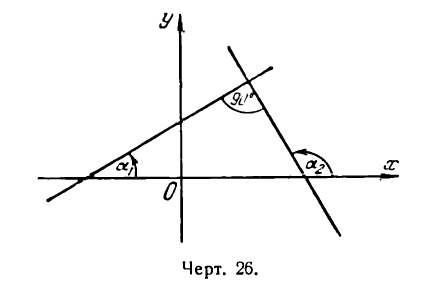
Пусть две прямые взаимно перпендикулярны и образуют с положительным направлением оси Ох углы а1 и а2 (рис. 26). В этом случае

т. е. данные прямые взаимно перпендикулярны.

Таким образом, если прямые взаимно перпендикулярны, то их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку (и наоборот).

Так, например, если у одной прямой угловой коэффициент

равен то у перпендикулярной ей прямой он равен .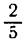

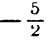
Пример:

Написать уравнение прямой, проходящей через точку А(—3; 5) и перпендикулярной прямой 4х — Зу—10 = 0.

Решение:

Через точку А проходит пучок прямых, среди которых находится и искомая прямая. Поэтому напишем сначала уравнение этого пучка

Чтобы выделить из него нашу прямую, нужно найти ее угловой коэффициент 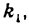связанный с угловым коэффициентом

данной прямой равенством (1). Но 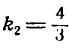следовательно,

Подставив в уравнение (2) вместо 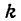найденное его значение

Это и есть искомое уравнение прямой. Преобразовав его, найдем:

Пересечение прямых

Пусть даны две прямые, определяемые уравнениями:

Требуется найти точку их пересечения.

Так как точка пересечения данных прямых есть их общая точка, то ее координаты должны удовлетворять как первому, так и второму уравнению, т. е. эти координаты должны быть общими корнями данных уравнений.

Чтобы найти эти корни, нужно, как известно из алгебры, решить совместно данные уравнения, рассматривая их как систему уравнений.

Пример:

Найти точку пересечения прямых

Решение:

Решим данные уравнения как систему. Умножив второе уравнение на 3 и сложив результат с первым уравнением, получим:

Зная х, находим у, например, из второго уравнения:

Пример:

Найти точку пересечения прямых

Решение:

Умножив все члены первого уравнения на —2 и сложив полученное уравнение со вторым, найдем:

что невозможно. Значит, данная система уравнений решений не имеет, а потому прямые, определяемые этими уравнениями, не имеют общих точек, т. е. данные прямые параллельны.

К этому же заключению можно прийти, сравнивая угловые коэффициенты данных прямых.

Видео:Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Дополнение к прямой линии

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Составление уравнения прямой с угловым коэффициентом по графикуСкачать

Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач

Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.

Видео:Угловой коэффициент прямой. Решение задач.Скачать

Угол наклона прямой и угловой коэффициент прямой

Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.

Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.

Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .

Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.

Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.

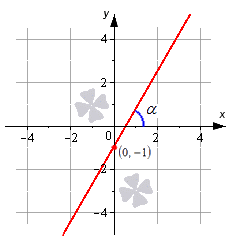
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.

Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.

Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .

Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .

Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .

Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .

Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .

Ответ: α = a r c t g 3 .

Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .

Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:

α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .

Ответ: 5 π 6 .

Видео:Уравнение прямой с угловым коэффициентомСкачать

Уравнение с угловым коэффициентом

Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .

Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.

Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.

Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.

Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.

Ответ: М 1 принадлежит прямой, а М 2 нет.

Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .

Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .

Видео:7 класс - Алгебра - Определение углового коэффициентаСкачать

Уравнение прямой с угловым коэффициентом, проходящей через заданную точку

Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .

Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .

Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .

Решение

По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .

Ответ: y = — 2 x + 7 .

Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .

По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:

y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1

Видео:Уравнение прямой с угловым коэффициентомСкачать

Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно

Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.

Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .

Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.

Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.

Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:

y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3

Ответ: x 1 = y — 12 — 3 .

Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.

Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?

Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:

y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0

Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .

Решим задачу обратную данной.

Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .

Результат и является уравннием с угловым коэффициентом, который равняется — A B .

Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.

Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:

2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .

Ответ: y = 1 6 x + 1 4 .

Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:

x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .

Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1

Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.

Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:

y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .

Ответ: y = 3 2 x — 3 .

Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.

Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:

5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x

Ответ: y = 5 2 x — 6 .

Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.

Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .

Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:

x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .

Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:

x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1

Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .

📹 Видео

УЧИМСЯ ПОНИМАТЬ ЛИНЕЙНУЮ ФУНКЦИЮ. Уравнения прямой с угловым коэффициентом, по точкам и в отрезкахСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Урок 5. Уравнение прямой с угловым коэффициентом. Декартовы координаты. Геометрия 9 класс.Скачать

Угловой коэффициент прямойСкачать

Составление уравнения прямой с угловым коэффициентомСкачать

Уравнение прямых с угловым коэффициентомСкачать

Как найти угловой коэффициент прямой. На что влияет угловой коэффициент. Урок 7. Геометрия 8-9 классСкачать

Угловой коэффициент в уравнении прямой. Геометрический смысл углового коэффициента. Геометрия 8 клСкачать

Уравнение прямой. Видеоурок 6. Геометрия 9 классСкачать

Угловой коэффициент прямой. Пример 1Скачать

Уравнение прямой на плоскостиСкачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать