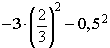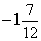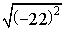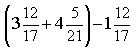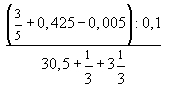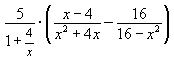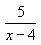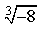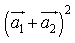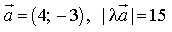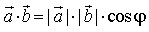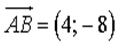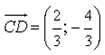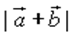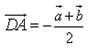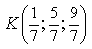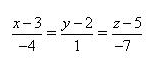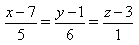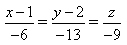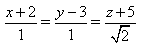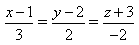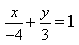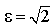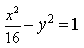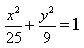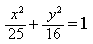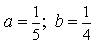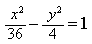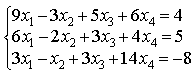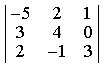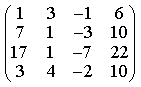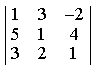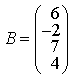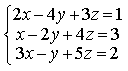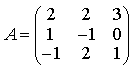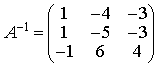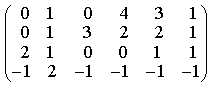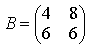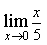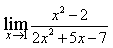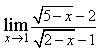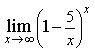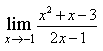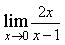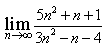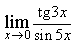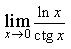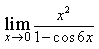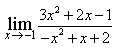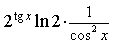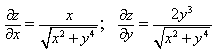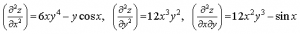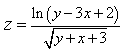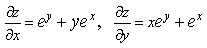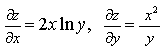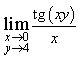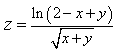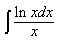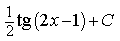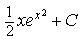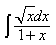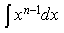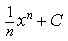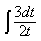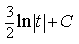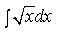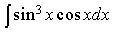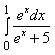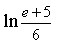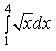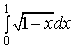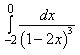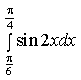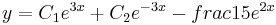Уравнение прямой проходящей через точку пересечения прямых 2x 3y 8 0

Математика | 1 — 4 классы

Найдите уравнение прямой, проходящей через точку пересечения прямых 2x + 3y — 8 = 0 и x — 4y + 5 = 0 и через точку M1( — 2 ; 3) Выберите один ответ :

2x + 3y — 8 = 0 иx — 4y + 5 = 0

2(4у — 5) + 3у — 8 = 0

х = 4 * 18 / 11 — 5 = 72 / 11 — 5 = 17 / 11

M1( — 2 ; 3) и точка(17 / 11 ; 18 / 11)

18 / 11 = 17 / 11k + m, 18 = 17k + 11m

18 = 17k + 11(3 + 2k)

18 = 17k + 33 + 22k

m = 3 + 2 * ( — 15 / 39)

m = 2 9 / 39 = 2 3 / 13

y = — 15 / 39x + 2 3 / 13 — уравнение прямой

у = — 5 / 13х + 2 3 / 13

Ответ : 13у + 5х — 29 = 0

Решением является последнее уравнение.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Составить уравнение прямой, проходящей через точку и начало координат пересечения прямых 2x + 5y — 8 = 0 и 2x + 3y + 4 = 0?

Составить уравнение прямой, проходящей через точку и начало координат пересечения прямых 2x + 5y — 8 = 0 и 2x + 3y + 4 = 0.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Написать уравнение прямой, проходящей через точку M пересечения прямых 2x + y + 6 = 0 и 3x + 5y −15 = 0 и через точку N (1 ; — 2)?

Написать уравнение прямой, проходящей через точку M пересечения прямых 2x + y + 6 = 0 и 3x + 5y −15 = 0 и через точку N (1 ; — 2).

Видео:№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать

Напишите уравнение прямой, проходящей через точку А (2 ; 5) и параллельной прямой, на которой лежат точки В( — 4 ; 3) и С( — 4 ; 1)?

Напишите уравнение прямой, проходящей через точку А (2 ; 5) и параллельной прямой, на которой лежат точки В( — 4 ; 3) и С( — 4 ; 1).

Видео:Видеоурок "Общие уравнения прямой"Скачать

Уравнение прямой проходящее через две точки?

Уравнение прямой проходящее через две точки.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Составить уравнение прямой, проходящей через точки?

Составить уравнение прямой, проходящей через точки.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

На прямую проходящею через точки а(1 ; — 2) и в(0 ; — 7) опущен перпендикуляр из точки с( — 3 ; 4)?

На прямую проходящею через точки а(1 ; — 2) и в(0 ; — 7) опущен перпендикуляр из точки с( — 3 ; 4).

Найти точку пересечения перпендикуляра с прямой ав.

Видео:Составляем уравнение прямой по точкамСкачать

Составьте уравнение прямой проходящей через точку А(1 ; 8) и точку В(0 ; 4)?

Составьте уравнение прямой проходящей через точку А(1 ; 8) и точку В(0 ; 4).

Видео:Часть 10 Уравнения прямой проходящей через точку пересечения прямых и имеющей заданное направлениеСкачать

Написать уравнение прямой, проходящей через начало координат и через точку пересечения прямых 3х + у — 5 = 0 и 2х + у + 1 = 0?

Написать уравнение прямой, проходящей через начало координат и через точку пересечения прямых 3х + у — 5 = 0 и 2х + у + 1 = 0.

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Найдите уравнение прямой параллельной у — 2х + 5 = 0 и проходящей через точку А(3 ; — 1)?

Найдите уравнение прямой параллельной у — 2х + 5 = 0 и проходящей через точку А(3 ; — 1).

Видео:№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать

Прямая параллельная прямой y = 2x + 1 и проходящая через точку (1 ; — 4) задается уравнением?

Прямая параллельная прямой y = 2x + 1 и проходящая через точку (1 ; — 4) задается уравнением.

На этой странице вы найдете ответ на вопрос Найдите уравнение прямой, проходящей через точку пересечения прямых 2x + 3y — 8 = 0 и x — 4y + 5 = 0 и через точку M1( — 2 ; 3) Выберите один ответ :3x + 8y — 18 = 0?. Вопрос соответствует категории Математика и уровню подготовки учащихся 1 — 4 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

5 + х = 5 х = 5 — 5 х = 0. У + 15 = 15 у = 15 — 15 у = 0. Х — 4 = 0 х = — 4. 28 — а = 28 а = 28 + 28 а = 56.

А) x = 5 — 5 = 0 b)y = 15 — 15 = 0 c)x = 0 + 4 = 4 d)a = 28 — 28 = 0.

А) 280, 70, 350, 20 б) 4600, 14000, 800, 3200 в) 3000, 9000, 26000, 25000 г) 5000000, 32000000.

А)280, 70, 350, 20 б)4600, 14000, 800, 3200 в) 3000, 9000, 26000, 25000 г)5000000, 32000000.

Представим, что x — это сколько страниц занимает расскуз, тогда x×3 — это сколько страниц занимает повесть x + (x×3) = 68 x + 3x = 68 4x = 68 x = 68 : 4 x = 17 — рассказ 17×3 = 51 — повесть.

Т. к. Собрали всего 61 орех, а вова собрал четное число, то остальные дети в сумме собрали нечетное количество( т. К. 61 — четное число = нечетное) и т. К. они собирали только нечетное количество значит детей было нечетное число( т. К. нечетное п..

1) 33 : 3 = 11 (кусков) картона разрезали 2) 17 — 11 = 6 (кусков) картона Ответ : 6 кусков картона осталось неразрезанными.

1)1000 : 100 = 10 2)904 3)450 : 10 = 45 4)1000 : 10 = 100 5)200 — 100 = 100.

1) 7(х + у) / 21 = х + у / 3 2)4(2m — n) / 4m = 2m — n / m 3)3(3a + 4b) / 3 = 3a + 4b 4)9(5c + 2d) / 27d = 5c + 2d / 3d 5)x(5 — y) / x = 5 — y 6)2m(3n — 2) / 2m = 3n — 2.

Возможно одинакого. Если Аня поймала 4, а Вера — 1 Боря — 3, Гена — 2.

Видео:Видеоурок "Уравнение прямой, проходящей через две точки"Скачать

Задача 22085 2) Найти уравнение прямой, проходящей.

Условие

2) Найти уравнение прямой, проходящей через точку пересечения прямых 2x-y-1=0 и 3x-y+4=0 параллельно прямой 4x+2y-13 = 0.

Решение

Вычитаем из второго уравнения первое
х+5=0
х=-5
тогда
у=2х-1=2*(-5)-1=-11

Переформулируем задачу: написать уравнение прямой, проходящей через точку (-5; -11) параллельно прямой
4х+2у-13=0

Нормальный вектор прямой vector=(4;2)
Если две прямые параллельны, то их нормальные векторы тоже.
Значит у искомой прямой тот же самый нормальный вектор vector=(4;2)
Уравнение прямой с заданным нормальным вектором vector=(A;B)и проходящей через точку (х_(о);у_(о)) имеет вид
A*(x-x_(o))+B*(y-y_(o))=0
4*(x-(-5))+2*(y-(-11))=0
4x+2y+42=0
О т в ет 4х+2у+42=0

Видео:Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Ответы на все модули (для контрольного теста) по предмету математика

Ответы на все модули (для контрольного теста) по предмету математика.

Ответы на модуль 1 (ЧИСЛА) по предмету математика.

1) Найдите значение выражения

2) Упростите иррациональное выражение

22

10000

6) Какое из перечисленных чисел является иррациональным?

3,141592…

7) Вычислите

6*5/21

8) Какая из перечисленных дробей является смешанной периодической дробью?

2,75(12)

9) Вычислите с точностью до десятых

0,3

10) Найдите значение выражения 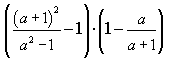при a= 2

2/3

11) Упростите

12) Найдите

-2

13) Какие числа называются целыми?

натуральные числа, числа противоположные натуральным, и число 0

Ответы на модуль 2 (ВЕКТОРНАЯ АЛГЕБРА) по предмету математика.

1) Дано: 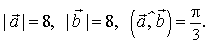Найдите a*b

32

2) Дано: Вычислите

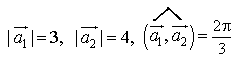
13

3) Найдите l , если

3 или -3

4) Что называется скалярным произведением двух векторов?

число, определяемое по формуле

5) Найдите l , если

2,5 или -2,5

6) Даны векторы 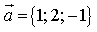и Найдите — проекцию вектора на ось вектора

7) Даны точки M(-5; 7; -6), N(7; -9; 9). Вычислите проекцию вектора 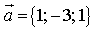на вектор MN

3

8) При каком значении l векторы MP и KD коллинеарны, если M(-3; 2), P(-1; -2), K(2; 1), D(5;l)?

-5

9) Какие векторы называются коллинеарными?

лежащие на одной прямой или параллельных прямых

10) Векторы называются компланарными, если

они лежат в одной плоскости или параллельных плоскостях

11) Какой из перечисленных векторов коллинеарен вектору

12) Векторы a и b взаимно перпендикулярны (ортогональны), причем |a|=5 и |b|=12 . Определите

13

13) Векторы AC=a и BD=d служат диагоналями параллелограмма ABCD. Выразите вектор DA через векторы a и b

Ответы на модуль 3 (АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ) по предмету математика.

1) Найдите координаты точки K пересечения прямой с плоскостью 2x+ 5y- 3z= 0

2) Найдите уравнение прямой, проходящей через точку пересечения прямых 2x + 3y — 8 = 0 и x — 4y + 5 = 0 и через точку M₁(-2; 3)

5x+ 13y— 29 = 0

3) Укажите канонические уравнения прямой, проходящей через точки M₁(3; 2; 5) и M₂(-1; 3; -2)

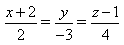
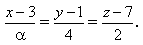
4) Даны прямые и При каком значении a они перпендикулярны?

a= 2

5) Установите взаимное расположение прямых 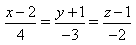и

прямые перпендикулярны

6) Укажите канонические уравнения прямой

7) Найдите острый угол между прямыми 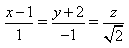и

60°

8) Составьте уравнение плоскости, проходящей через параллельные прямые 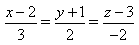и

9) Даны вершины треугольника ABC: A(3; -1),B(4; 2) и C(-2; 0). Напишите уравнения его сторон

10) Уравнение 3x— 4y+ 12 = 0 преобразуйте к уравнению в отрезках

11) Определите уравнение прямой, отсекающей на оси Oy отрезок b = 2 и составляющей с осью Ox угол j= 45°

12) Найдите координаты точки пересечения прямых 2x—y— 3 = 0 и 4x+ 3y— 11 = 0

(2; 1)

13) Найдите уравнение прямой, проходящей через точки M₁(3; 2), M₂(4;-1)

Ответы на модуль 4 (КРИВАЯ 2-ГО ПОРЯДКА) по предмету математика.

1) Определите эксцентриситет равносторонней гиперболы

2) Укажите уравнение окружности, которая проходит через точки А(3;1) и В(-1; 3), а ее центр лежит на прямой 3x—y— 2 = 0

(x— 2) 2 + (y— 4) 2 = 10

3) Укажите уравнение окружности радиуса R= 8 с центром в точке C(2;-5)

(x— 2) 2 + (y+ 5) 2 = 8 2

4) Определите полуоси гиперболы

5) Укажите уравнение окружности, центр которой совпадает с началом координат, а прямая 3x— 4y+ 20 = 0 является касательной к окружности

x 2 +y 2 = 16

6) Укажите уравнение окружности, которая проходит через точку А(2;6) и ее центр совпадает с точкой C(-1; 2)

(x+ 1) 2 + (y— 2) 2 = 25

7) Укажите каноническое уравнение эллипса, расстояние между фокусами которого равно 8, а малая полуось b= 3

8) Напишите уравнение эллипса, если даны его полуоси a= 5 и b= 4

9) Укажите уравнение окружности, проходящей через точку (4; 5) с центром в точке (1; -3)

(x— 1) 2 + (y+ 3) 2 = 73

10) Определите полуоси гиперболы 25x 2 — 16y 2 =1

11) Напишите уравнение гиперболы, фокусы которой лежат на оси Ox, если даны a= 6 и b= 2

12) Укажите уравнение параболы, с вершиной в точке O и фокусом F(4; 0)

13) Укажите уравнение окружности, для которой точки А(3; 2) и В(-1; 6) являются концами одного из диаметров

(x— 1) 2 + (y— 4) 2 = 8

Ответы на модуль 5 (КРИВАЯ 2-ГО ПОРЯДКА) по предмету математика.

1) Найдите общее решение системы

2) Вычислите определитель

-89

3) Найдите ранг и базисные строки матрицы

2. 1-я строка, 2-я строка

4) Вычислите определитель

0

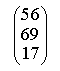
5) Найдите А × В, где ;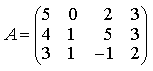

6) Решите систему уравнений методом Крамера

7) Найдите обратную матрицу для матрицы

8) Найдите ранг матрицы

4

9) Определитель системы трех линейных уравнений с тремя неизвестными равен 5. Это означает, что

система имеет единственное решений

11) Метод Гаусса решения системы линейных уравнений предполагает использование

последовательного исключения неизвестных

12) Система линейных уравнений называется совместной, если

она имеет хотя бы одно решение

13) Решите матричное уравнение AX + AXA = B, где ;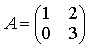

Ответы на модуль 6 (МАТЕМАТИЧЕСКИЙ АНАЛИЗ) по предмету математика.

1) Найдите предел

3

2) Найдите предел

5

3) Найдите предел

5

4) Найдите предел

1/e

5) Найдите предел

0

6) Найдите предел

0

7) Найдите предел

8) Найдите предел

1/2

9) Найдите предел

e — 5

10) Найдите предел

1

11) Найдите предел

0

12) Найдите предел

5/3

13) Найдите предел

3/5

Ответы на модуль 7 (ДИФФЕРЕНЦИРОВАНИЕ) по предмету математика.

1) Вычислите предел по правилу Лопиталя

0

2) Найдите производную функции f(x)=(1+ cos x)sin x

cos x+ cos 2x

3) Вычислите предел по правилу Лопиталя

1/18

4) Вычислите предел по правилу Лопиталя

-4/3

5) Найдите производную функции y= sin(2x 2 + 3)

4xcos(2x 2 + 3)

6) Найдите производную функции y=(3e x +x)× cos x

(3e x + 1) × cos x— (3e x +x) × sin x

7) Для функции 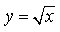найдите y(49)

1/14

8) Найдите производную функции

9) Найдите производную функции y=2 tg x

10) Найдите производную функции

11) Найдите скорость тела, движущего по закону S=3t-5

3

12) Дана функция 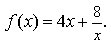Решите уравнение

13) Найдите производную функции y=xe x —e x

xe x

Ответы на модуль 8 (ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНОЙ) по предмету математика.

1) Число f(x₀) называется наибольшим значением функции на отрезке [a;b], если

для всех x из этого отрезка выполняется неравенство f(x) 2 — 3x+ 1

убывает при x 3/2

3) Найдите точки максимума (минимума) функции y=- 5x 2 — 2x+ 2

(-0,2;2,2) — точка максимума

4) Каково необходимое условие возрастания функции?

если функция y=f(x) дифференцируема и возрастает на интервале (a;b), то f(x)>=0 для всех xиз этого интервала

5) Определите поведение функции y= 2x 2 при x= 1

возрастает

6) В каких точках выпукла или вогнута кривая y=x 2 — 3x+ 6

вогнута во всех точках

7) Найдите промежутки возрастания или убывания функции y=- 2x 2 + 8x— 1

(0; 0)

9) Найдите точки перегиба кривой y=x 4 — 12x 3 + 48x 2 — 50

(2; 62) и (4; 206)

10) Найдите точки максимума (минимума) функции y=x 2 — 2x

(1;-1) — точка минимума

11) Вертикальные асимптоты к графику функции 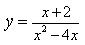имеют вид

12) Найдите наибольшее и наименьшее значения функции y=x 2 на промежутке [-1; 3]

13) В каких точках выпукла или вогнута кривая y= 2 — 3x—x 2

выпукла во всех точках

Ответы на модуль 9 (ФУНКЦИЯ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ) по предмету математика.

1) Найдите частные производные функции двух переменных

2) Найдите частные производные второго порядка функции z=x 3 y 4 +ycos x

3) Найдите предел функции 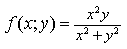при x->0, y->0

0

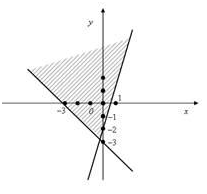
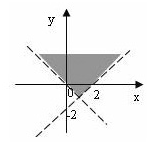
4) На каком из рисунков изображена область определения функции

5) Найдите частные производные функции двух переменных z=xe y +ye x

6) Найдите частные производные функции z=x 2 × ln y

7) Найдите полный дифференциал функции z=x 2 y+xy 2

8) Какая поверхность называется графиком функции n переменных?

9) Укажите полное приращение функции f(x;y)

10) Найдите

4

11) Укажите частное приращение функции f(x;y)по переменной у

12) На каком из рисунков изображена область определения функции

13) Найдите область определения функции

xy 2 не =y 2

Ответы на модуль 10 (НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ) по предмету математика.

1) Найдите

2) Найдите

3) Найдите

4) Найдите

5) Найдите

6) Найдите

7) Найдите

8) Найдите

9) Найдите

10) Найдите 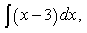если при x= 2 первообразная функция равна 9

11) Найдите

12) Найдите 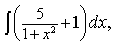если при x=0 первообразная функция равна 0

13) Найдите

Ответы на модуль 11 (ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ) по предмету математика.

1) Скорость точки, движущейся прямолинейно, задана уравнением v=9t 2 -2t-8. Вычислите путь, пройденный точкой за 3 с от начала движения

48 м

2) Вычислите определенный интеграл

9

3) Сила в 6 кГ растягивает пружину на 8 см. Какую работу она производит?

0,24 кГм

4) Вычислите определенный интеграл

5) Вычислите определенный интеграл

e p -1

6) Найдите площадь фигуры, заключенной между прямыми y=4x— 5, x=-3, x=-2 и осью Ox

15

7) Скорость падающего в пустоте тела определяется по формуле v= 9,8t м/сек. Какой путь пройдет тело за первые 10 секунд падения?

490 м

8) Найдите площадь фигуры, ограниченной прямыми y=5x, x=2 и осью Ox

10

9) Вычислите определенный интеграл

2

10) Вычислите определенный интеграл

4*2/3

11) Вычислите определенный интеграл

2/3

12) Вычислите определенный интеграл

0,24

13) Вычислите определенный интеграл

0,25

Ответы на модуль 12 (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ) по предмету математика.

1) Как называется решение, полученное из общего при конкретных значениях произвольных постоянных?

частным решением

2) Найдите общее решение уравнения (x+y)dx+xdy=0

3) При решении каких уравнений используют подстановку

при решении однородных уравнений

4) Найдите общее решение уравнения xy 2 dy=(x 3 +y 3 )dx

5) Среди перечисленных дифференциальных уравнений укажите уравнение Бернулли

6) Найдите общее решение уравнения y — 9y = e 2 x

7) Найдите общее решение уравнения

8) Найдите частное решение уравнения ds=(4t-3)dt, если при t= 0 s= 0

9) Найдите общее решение уравнения y—y= 0

10) Найдите общее решение уравнения

11) Среди перечисленных дифференциальных уравнений укажите однородное уравнение

12) Найдите общее решение уравнения y— 4y+ 3y= 0

13) Найдите общее решение уравнения y = cos x

Ответы на модуль 13 (РЯДЫ) по предмету математика.

1) Исследуйте сходимость ряда

сходится

2) Найдите интервал сходимости ряда x+2x 2 +3x 3 +4x 4 +…+nx n +…, не исследуя концов интервала

(-1; 1)

3) Найдите радиус сходимости ряда

4) Разложите в степенной ряд f(x)= arctg 3x

5) Исследуйте сходимость ряда

расходится

6) Исследуйте сходимость ряда

сходится

7) Найдите интервал сходимости ряда

8) Исследуйте сходимость ряда

расходится

9) Исследуйте сходимость ряда

расходится

10) Исследуйте сходимость ряда

сходится

11) Разложите в степенной ряд f(x)= sin 2x

12) Исследуйте сходимость ряда

расходится

13) Исследуйте сходимость ряда

сходится

Ответы на задачник по предмету математика.

1) Составьте уравнение плоскости, зная, что точка А(1, -1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.

x — y + 3z — 11 = 0

2) Вычислить определитель D, разложив его по элементам второго столбца.

-20

3) Вычислить J= ∫cos(lnx) dx/x

sin(lnx)+ C

4) Найти lim _x—>0 (5 x — cos x)

0

5) Вычислить площадь фигуры, ограниченной линиями 4y = x 2 , y 2 = 4x.

16/3

6) Найти производную функции y =ln sinx

ctg x

7) Найдите угол между векторами a = 2m+4n и b = m-n, где m и n — единичные векторы и угол между m и n равен 120 о

120

8) Найти наименьшее значение функции y = x 2 – 6x + 5 на отрезке (1,2).

-3

X1=2, X2=3, X3=-2.

10) При каком положительном значении параметра t прямые, заданные уравнениями
3tx — 8y + 1 = 0 и (1+t)x — 2ty = 0, параллельны?

🎦 Видео

УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Часть 11 Уравнение прямой проходящей через точку пересечения двух заданных прямых и заданную точкуСкачать

Уравнение прямой, проходящей через данную точку в данном направленииСкачать

Найти точку пересечения прямой и плоскостиСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Уравнение прямой.Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

12. Уравнения прямой в пространстве Решение задачСкачать