Уравнение прямой проходящей через точку и образующей с осью ох угол

Пусть прямая пересекает ось Оу в точке В (0; b) и образует с осью Ох

Итак, мы доказали, что координаты каждой точки прямой удовлетворяют уравнению (4.2). Нетрудно показать, что координаты любой точки, не лежащей на прямой, не удовлетворяют уравнению (4.2).

Уравнение (4.2) называется уравнением прямой с угловым коэффициентом.

Рассмотрим частные случаи уравнения (4.2).

• 1. Если b = 0, то получаем у = кх — уравнение прямой, проходящей через начало координат и образующей при к = tg а > О острый угол а с осью Ох, а при к = tg а ТО прямая перпендикулярна оси Ох (см.

рис. 4.6) и к = tg— не существует, т.е. вертикальная прямая не 2

имеет углового коэффициента. Предположим, что эта прямая отсекает на оси Ох отрезок, равный а. Очевидно, что уравнение такой прямой х = а (так как абсцисса любой точки прямой равна а), а уравнение оси Оу есть х = 0.

Уравнение прямой, проходящей через данную точку в данном направлении. Пусть прямая проходит через точку М_х(х_х ,у_х) и

образует с осью Ох угол а (рис. 4.7).

Так как точка М_х(х_х,у_х) лежит на прямой, то ее координаты удовлетворяют уравнению (4.2), т.е.

Вычитая равенство (4.3) из равенства (4.2), получим уравнение искомой прямой

Уравнение пучка прямых. Если в уравнении (4.4) к — произвольное число, то это уравнение определяет пучок прямых, проходящих через точку М_х(х_х,у_х), кроме прямой, параллельной оси Оу и не имеющей углового коэффициента (рис. 4.8).

О Пример 4.2. 1. Составить уравнение

прямой, проходящей через точку А (3;—2):

а) под углом 135° к оси Ох б) параллельно оси Оу. 2. Найти уравнение пучка прямых.

Решение. 1. а) угловой коэффициент прямой k = tg 135° = — 1.

Уравнение прямой, проходящей через точку А (3; —2) (см. рис. 4.9), по формуле (4.4) имеет вид у + 2 = — 1 (х —3) или у = —х + 1.

• б) Уравнение прямой, параллельной оси Оу, х = 3.
• 2. Уравнение пучка прямых, проходящих через точку А (3; —2),

Для составления уравнения прямой М_х М₂ (рис. 4.10) запишем уравнение пучка прямых, проходящих через точку М_х:

Так как точка М₂ <х₂,у₂) лежит на данной прямой, то чтобы выделить ее из пучка, подставим координаты точки М₂ в уравнение пучка у₂

хj) и найдем угловой коэффициент прямой

Теперь уравнение искомой прямой примет вид или

[> Пример 4.3. Составить уравнение прямой, проходящей через точки А (-5; 4) и В (3; —2).

Р е ш е н и е. По уравнению (4.6): —- = ———, откуда по

сле преобразований у = — х + —. ?

Уравнение прямой в отрезках. Найдем уравнение прямой по заданным отрезкам аФ 0 и b ф 0, отсекаемым на осях координат. Используя (4.6), уравнение прямой, проходящей через точки А <а;0) и В (0; Ь)

(рис. 4.11), примет вид — = —

или после преобразований

О Пример 4.4. Составить уравнение прямой, проходящей через точку А (2; —1), если эта прямая отсекает от положительной полуоси Оу отрезок, вдвое больший, чем на положительной полуоси Ох (рис. 4.12).

Р е ш е н и е. По условию b = 2а (а >0, b > 0). Подставляя это выражение в

уравнение (4.7), получим — + — = 1.

Так как точка А (2; —1) лежит на прямой, то ее координаты удовлетворяют 2 1

этому уравнению, т.е. — — — =1, от- а 2 а

Итак, уравнение искомой прямой имеет вид — + — = 1 или у = —2х + 3. ?

Общее уравнение прямой и его исследование. Рассмотрим уравнение первой степени с двумя переменными в общем виде

в котором коэффициенты А и В не равны одновременно нулю, т.е. А 2 + В 2 ф 0.

1. Пусть В ф 0. Тогда уравнение (4.8) можно записать в виде ₌ А _ С

А/В, b = —С/В. Если А ф 0, С ф 0, то получим у = кх + b (уравнение прямой с угловым коэффициентом); если А ф 0, С = 0, то у = кх (уравнение прямой, проходящей через начало координат); если А = 0, С ф 0, то у = b (уравнение прямой, параллельной оси Оу); если А = 0, С = 0, то у = 0 (уравнение оси Ох).

2. Пусть В = 0, А ф 0. Тогда уравнение (4.8) примет вид С

х =—. Обозначим а = —С/А. Если С ф 0, то получим х = а

(уравнение прямой, параллельной оси Оу); если С = 0, то х = 0 (уравнение оси Оу).

Уравнение (4.8) называется общим уравнением прямой. Заметим, что в отличие от уравнения пучка прямых (4.4) общее уравнение (4.8) включает и уравнение любой вертикальной прямой, параллельной оси Оу.

Видео:Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач

Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.

Видео:Уравнение прямой линии с угловым коэффициентом проходящей через точкуСкачать

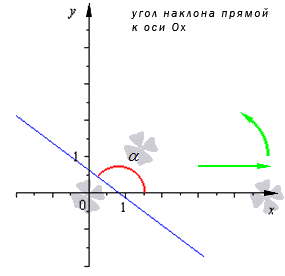
Угол наклона прямой и угловой коэффициент прямой

Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.

Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.

Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .

Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.

Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.

Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.

Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.

Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .

Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .

Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .

Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .

Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .

Ответ: α = a r c t g 3 .

Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .

Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:

α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .

Ответ: 5 π 6 .

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Уравнение с угловым коэффициентом

Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .

Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.

Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.

Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.

Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.

Ответ: М 1 принадлежит прямой, а М 2 нет.

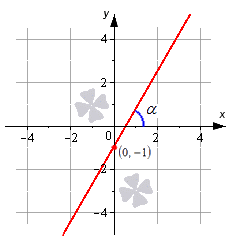
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .

Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .

Видео:Уравнение прямой, проходящей через точку параллельно OX, OY или через начало координат. Урок 5. 8 клСкачать

Уравнение прямой с угловым коэффициентом, проходящей через заданную точку

Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .

Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .

Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .

Решение

По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .

Ответ: y = — 2 x + 7 .

Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .

По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:

y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно

Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.

Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .

Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.

Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.

Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:

y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3

Ответ: x 1 = y — 12 — 3 .

Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.

Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?

Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:

y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0

Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .

Решим задачу обратную данной.

Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .

Результат и является уравннием с угловым коэффициентом, который равняется — A B .

Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.

Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:

2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .

Ответ: y = 1 6 x + 1 4 .

Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:

x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .

Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1

Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.

Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:

y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .

Ответ: y = 3 2 x — 3 .

Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.

Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:

5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x

Ответ: y = 5 2 x — 6 .

Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.

Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .

Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:

x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .

Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:

x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1

Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .

Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Уравнение прямой, проходящей через точку A ( — 2, 3) и образующей с осью Ох угол 45 градусов, 90 и 0?

Математика | 1 — 4 классы

Уравнение прямой, проходящей через точку A ( — 2, 3) и образующей с осью Ох угол 45 градусов, 90 и 0.

Поскольку уравнение прямой образует с осью OX угол в 45⁰, значит.

Угловой коэффициент прямой будет равен :

(угловой коэффициент это коэффициент при х в уравнении графика).

Для 90 градусов :

Видео:Уравнение прямой, проходящей через начало координатСкачать

Уравнение прямой, проходящей через точку?

Уравнение прямой, проходящей через точку.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Срочно помогите?

Cоставить уравнение прямой проходящую через точку (0 ; — 2) и составляющей с положительным направлением оси ОХ такой же угол, что и прямая y = 3 / 7x — 3.

Видео:Видеоурок "Канонические уравнения прямой"Скачать

Напишите уравнение прямой , проходящей через точку N( — 2 ; 3) и параллельно оси х?

Напишите уравнение прямой , проходящей через точку N( — 2 ; 3) и параллельно оси х.

Видео:Угловой коэффициент прямойСкачать

Написать уравнение прямой, проходящей через точку С(1 ; 2 ; 4) и перпендикулярной к оси ОY?

Написать уравнение прямой, проходящей через точку С(1 ; 2 ; 4) и перпендикулярной к оси ОY.

Видео:Видеоурок "Уравнение прямой, проходящей через две точки"Скачать

Опишите на алгеброическом языке : помогите плииииииииз ?

Опишите на алгеброическом языке : помогите плииииииииз !

А)Прямую, проходящую через точку 5 оси координат и параллельную оси абсцисс

Б) прямую проходящую через точку ( — 5 ; 2) и паралельную оси ординат.

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Запишите уравнение прямой параллельной оси х и проходящей через точку (2 ; — 3)?

Запишите уравнение прямой параллельной оси х и проходящей через точку (2 ; — 3).

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Составьте уравнение прямой проходящей через точку A (1 ; — 2) если она параллельна оси абсцисс?

Составьте уравнение прямой проходящей через точку A (1 ; — 2) если она параллельна оси абсцисс.

Видео:12. Уравнения прямой в пространстве Решение задачСкачать

Составьте уравнение прямой, которая проходит через точку A(корень из 3 ; 5) и образует с положительным направлением оси абцисс угол 60 градусов?

Составьте уравнение прямой, которая проходит через точку A(корень из 3 ; 5) и образует с положительным направлением оси абцисс угол 60 градусов.

Видео:Составляем уравнение прямой по точкамСкачать

Составить уравнение прямой, проходящей через начало координат, если она образует с положительным направлением оси Ох угол А — 45°?

Составить уравнение прямой, проходящей через начало координат, если она образует с положительным направлением оси Ох угол А — 45°.

Видео:Часть 8 Уравнение прямой проходящей через точку и перпендикулярную к заданной прямойСкачать

Составьте уравнение прямой, проходящей через точку (5 ; — 7) и образующей с осью Ox угол arctg( — 2)?

Составьте уравнение прямой, проходящей через точку (5 ; — 7) и образующей с осью Ox угол arctg( — 2).

На странице вопроса Уравнение прямой, проходящей через точку A ( — 2, 3) и образующей с осью Ох угол 45 градусов, 90 и 0? из категории Математика вы найдете ответ для уровня учащихся 1 — 4 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

1)30 + 2 = 32 2)32 + 2 = 34 3)34 + 2 = 36 4)36 + 2 = 38 5)38 + 2 = 40 6)40 + 2 = 42 места в 7 ряду.

1 ряд — 30 2 ряд — 32 3 ряд — 34 4 ряд — 36 5 ряд — 38 6 ряд — 40 7 ряд — 42 Следовательно, в 7 ряду 42 мест.

То что угол это угол хDDD.

На каждого токаря приходится 738 : 6 = 123 деталей если одного токаря не будет бригада наточит 738 — 123 = 615 деталей БЕЗОБРАЗИЕ. Срыв плана. Лишение премии. ПОЛНЫЕ УБЫТКИ.

Русский знаеш ? А то я русскй.

За 5 шо спортсмен пробіг 15 м скільки він пробіг за 1 год Скільки м проїхав велосипедист, якщо продуктивність його праці на 1 год на 2 м більша ніж у спортсмена і він їхав 6 год.

3) 12 : 30 4) Футбольный Уроки в школе начинаются матч начинается в 8 часов утра в половине четвёртого.

111 × 11 — 111 + 1 = 1111.

1)48 6 = 8(км) — прошли пешком 2)48 2 = 24(км) — проехали на автобусе 3)48 — (24 + 8) = 16(км) — осталось пройти Ответ : 16 километров осталось пройти.

🔍 Видео

Уравнение прямой, проходящей через данную точку в данном направленииСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать