Уравнение прямой проходящей через точку а4 перпендикулярно плоскости а1а2а3

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через данную точку и перпендикуляной данной плоскости. Дается подробное решение с пояснениями. Для построения уравнения прямой введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости

Наша цель построить уравнение прямой, проходящей через данную точку M₀ и перпендикулярной к данной плоскости Ax+By+Cz+D=0.

Общее уравнение плоскости имеет вид:

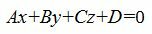(1)

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

(2)

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

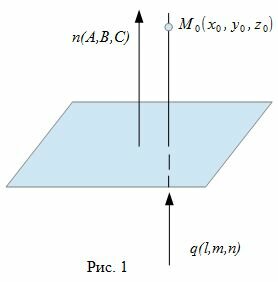Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональный плоскости (1) имеет следующий вид:

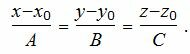(3)

Пример 1. Построить прямую, проходящую через точку M₀(5, -4, 4) и перпендикулярной плоскости

Общее уравнение плоскости имеет вид (1), где :

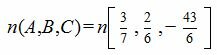(4)

Подставляя координаты точки M₀(5, -4, 4) и координаты нормального вектора плоскости (4) в (3), получим:

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Уравнения прямой, которая проходит через заданную точку и перпендикулярна к заданной плоскости.

В этой статье мы разберемся с нахождением уравнений прямой, которая в прямоугольной системе координат в трехмерном пространстве проходит через заданную точку и перпендикулярна к заданной плоскости. Сначала разберем принцип составления уравнений такой прямой, после чего перейдем к решению задач.

Навигация по странице.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Принцип составления уравнений прямой, проходящей через заданную точку перпендикулярно к заданной плоскости.

Прежде чем приступить к составлению уравнений прямой, которая проходит через заданную точку пространства перпендикулярно к заданной плоскости, освежим в памяти один момент.

В 10 классе на уроках геометрии доказывается теорема: через любую точку трехмерного пространства проходит единственная прямая, перпендикулярная к заданной плоскости. Таким образом, мы можем определить конкретную прямую, указав точку, через которую она проходит, и плоскость, к которой она перпендикулярна.

Сформулируем условие задачи.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , задана точка , плоскость и требуется написать уравнения прямой a , проходящей через точку М₁ перпендикулярно к заданной плоскости .

Решим эту задачу.

Нам известны координаты точки M₁ , через которую проходит прямая a , уравнения которой нам требуется найти. Но этого мало, чтобы записать уравнения прямой a . Если мы будем знать еще координаты направляющего вектора прямой a , то сможем записать канонические уравнения прямой a в пространстве и параметрические уравнения прямой a в пространстве.

Как же определить координаты направляющего вектора прямой a ? Да очень просто. Так как по условию прямая a перпендикулярна к плоскости , то нормальный вектор плоскости является направляющим вектором прямой a . Таким образом, нам остается отыскать координаты нормального вектора плоскости , принять их за соответствующие координаты направляющего вектора прямой a и записать требуемые уравнения прямой a .

В свою очередь координаты нормального вектора плоскости находятся в зависимости от способа задания плоскости в прямоугольной системе координат Oxyz . Если плоскости в прямоугольной системе координат Oxyz отвечает общее уравнение плоскости вида , то нормальным вектором плоскости является вектор . Если плоскость задается уравнением плоскости в отрезках , то от него следует перейти к общему уравнению плоскости , откуда станут видны координаты нормального вектора плоскости : . Если плоскость задана каким-либо другим способом (например, с помощью трех точек, не лежащих на одной прямой, или с помощью уравнений двух пересекающихся прямых, или с помощью уравнений двух параллельных прямых), то на основании этих данных следует определить общее уравнение плоскости , откуда получить координаты ее нормального вектора.

Итак, задача нахождения уравнений прямой, которая проходит через заданную точку пространства и перпендикулярна к заданной плоскости, решена. Осталось лишь рассмотреть несколько решенных примеров.

Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Примеры нахождения уравнений прямой, которая проходит через заданную точку пространства и перпендикулярна к заданной плоскости.

В этом пункте статьи мы приведем подробные решения наиболее характерных задач, в которых находятся уравнения прямой, проходящей через заданную точку пространства перпендикулярно к заданной плоскости.

Начнем с самого простого случая, когда требуется написать уравнения прямой, проходящей через заданную точку перпендикулярно к одной из координатных плоскостей.

Напишите канонические уравнения прямой a , которая проходит через точку и перпендикулярна координатной плоскости Oyz .

Нормальным вектором координатной плоскости Oyz является координатный вектор . Так как прямая a перпендикулярна плоскости Oyz , то является ее направляющим вектором. Итак, мы знаем координаты точки, лежащей на прямой a , и координаты ее направляющего вектора, то есть, можем написать ее канонические уравнения: .

.

Аналогично решается задача, в условии которой даны координаты точки, через которую проходит прямая, и задана плоскость с помощью общего уравнения плоскости.

Составьте параметрические уравнения прямой a , проходящей через точку перпендикулярно к плоскости .

Направляющим вектором прямой a является нормальный вектор плоскости , то есть, . Теперь мы можем записать требуемые уравнения прямой a . Они имеют вид .

.

В заключении рассмотрим пример составления уравнений прямой, которая проходит через заданную точку пространства и перпендикулярна к плоскости, заданной тремя не лежащими на одной прямой точками.

В прямоугольной системе координат Oxyz в трехмерном пространстве заданы три точки . Напишите уравнения прямой a , проходящей через начало координат перпендикулярно к плоскости ABC .

Направляющим вектором прямой, проходящей через начало координат перпендикулярно к плоскости АВС , является нормальный вектор плоскости АВС . Нормальным вектором плоскости АВС является векторное произведение векторов и . Найти указанное векторное произведение мы сможем, если будем знать координаты векторов и . Вычислим координаты векторов и по координатам точек А , В и С (при необходимости смотрите статью нахождение координат вектора по координатам точек его конца и начала): .

Тогда, , а в координатной форме (при необходимости обращайтесь к статье координаты вектора).

Теперь мы можем записать требуемые уравнения прямой a , которая проходит через точку и перпендикулярна к плоскости ABC : .

Приведем второй способ решения этой задачи.

Составим уравнение плоскости, проходящей через три заданные точки А , В и С , , откуда виден нормальный вектор этой плоскости . Далее принимаем этот вектор за направляющий вектор прямой a и записываем ее уравнения.

.

Видео:Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать

Уравнение прямой проходящей через точку а4 перпендикулярно плоскости а1а2а3

Даны четыре точки A1( 5; 3; 7), A2 (-2; 3; 7), A3(4; 2; 10), A4(1; 2; 7).

а) плоскости А1А2А3;

Находим векторы А1А2 и А1А3.

А1А2 = (-2-5; 3-3; 7-7) = (-7; 0; 0).

А1А3 = (4-5; 2-3; 10-7) = (-1; -1; 3).

Нормальный вектор плоскости А1А2А3 находим из векторного произведения векторов А1А2 и А1А3.

-1 -1 3| -1 -1 = 0i + 0j + 7k + 21j + 0i + 0k =

Нормальный вектор плоскости А1А2А3 равен (0; 21; 7).

Подставляем найденные координаты нормального вектора в уравнение плоскости:

21y+7z−112=0 или после сокращения на 7:

Уравнение А1А2А3: 3y + z — 16.

Из этого уравнения можно принять нормальный вектор плоскости А1А2А3 равным (0; 3; 1).

Направляющий вектор найден выше: А1А2 = (-7; 0; 0).

Уравнение А1А2: (x — 5)/(-7) = (y — 3)/0 = (z — 7)/0.

Это уравнение прямой, параллельной оси абсцисс.

в) прямой А4М перпендикулярной к плоскости А1А2А3;

Направляющим вектором прямой А4М является нормальный вектор плоскости А1А2А3, найденный ранее и равный (0; 3; 1).

Уравнение А4М: (x — 1)/0 = (y — 2)/3 = (z — 7)/1.

г) прямой А3 N параллельной прямой А1А2.

У этой прямой направляющий вектор равен вектору А1А2,

Уравнение А3N: (x — 4)/(-7) = (y — 2)/0 = (z — 10)/0.

Это уравнение прямой, параллельной оси абсцисс.

д) плоскости проходящей через точку А4 перпендикулярно к прямой А1 А2.

У этой плоскости нормальный вектор совпадает с вектором А1А2.

после сокращения на -7 получаем

x – 1 = 0.

e) синус угла между прямой A1A4 и плоскостью A1A2A3.

= 21 = 0,23009

Угол равен 0,23217 радиан или 13,3023 градуса.

ж) косинус угла между координатной плоскостью Oxy и плоскостью A1A2A3.

Координатная плоскость Oxy имеет уравнение z = 0.

Уравнение плоскости А1А2А3: 3y + z — 16.

Вычислим угол между плоскостями

z = 0 и 3y + z – 16.

cos α = |A1·A2 + B1·B2 + C1·C2|/(√(A1² + B1² + C1²)* √(A2² + B2² + C2²)).

cos α = |0·0 + 0·3 + 1·1|/(√(0² + 0² + 1²)* √(0² + 3² + 1²)) =

= |0 + 0 + 1|/(√(0 + 0 + 1)* √(0 + 9 + 1)) =

= 1/√1* √10 = 1/√10 = √10/10 ≈ 0,3162.

🎦 Видео

Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать

Часть 8 Уравнение прямой проходящей через точку и перпендикулярную к заданной прямойСкачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

12. Уравнения прямой в пространстве Решение задачСкачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Уравнение параллельной прямойСкачать

9 класс, 7 урок, Уравнение прямойСкачать

2. Уравнение плоскости примеры решения задач #1Скачать

Видеоурок "Уравнение прямой, проходящей через две точки"Скачать