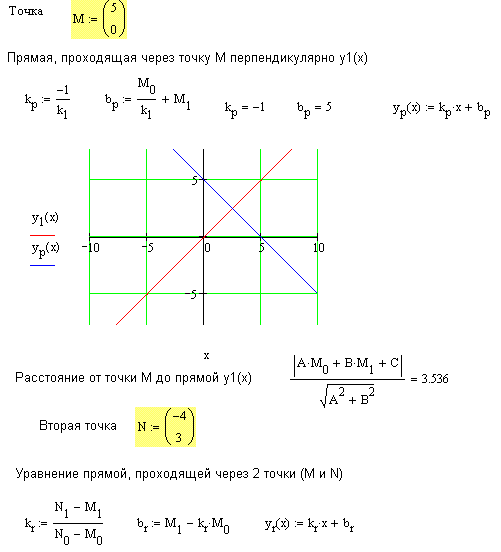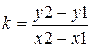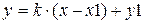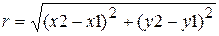Уравнение прямой по двум точкам mathcad (7 видео)

Уравнение прямой по двум точкам mathcad

Pers.narod.ru. Обучение. Прямая на плоскости в MathCAD

В приложенном документе выполняются:

проверка существования прямой и её расположение (параллельна оси 0x, проходит через начало координат и т.д.);
уравнение прямой с угловым коэффициентом;
угол между двумя прямыми в градусах и координаты точки пересечения 2 прямых;
прямая, проходящая через точку M перпендикулярно первой прямой;
расстояние от точки до прямой;
уравнение прямой, проходящей через 2 точки M и N;
строятся соответствующие графики.

Фрагмент документа:

Скачать этот пример в формате MCD (20 Кб)

Содержание

Построение прямой, проходящей через две заданные точки
Лекция 8
Что будем делать с полученным материалом:
Все темы данного раздела:
Осваиваем Mathcad (стр. 10 )
🎥 Видео

Видео:Составляем уравнение прямой по точкамСкачать

Построение прямой, проходящей через две заданные точки

Построение прямой, проходящей через две заданные точки — раздел Образование, Лекция 8 Даны Две Точки A (X1, Y1) И B(X2, Y2). Задано X1=-1, Y1=-1, X2=1, Y2=1. Через.

Даны две точки A (x1, y1) и B(x2, y2). Задано x1=-1, y1=-1, x2=1, y2=1. Через эти точки надо провести прямую линию и найти расстояние между ними.

Уравнение прямой может быть записано так:

Угловой коэффициент определяется формулой:

Уравнение можно записать:

Расстояние между двумя точками вычисляется по формуле:

На рис.8.27 приведено решение этой задачи в системе Mathcad. Обратите внимание на форматирование графика и использование текстового блока для того, чтобы пометить точку A и B.

Рисунок 8.27 — График прямой, проходящей через две заданные точки

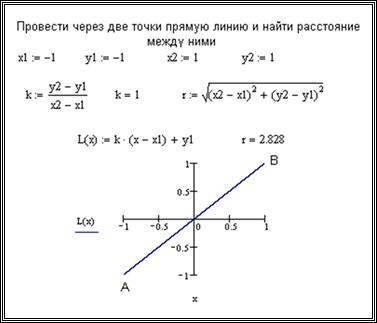
8.5.2 Построение графика функции y = f(x), графика первой и второй производной этой функции

Найти производную первого и второго порядка функции y = f(x) и на одном графике построить график функции y = f(x), график первой и второй производной этой функции. Решение этой задачи приведено на рис.8.28.

Рисунок 8.28 — График функции y = f(x), первой и второй производной этой функции

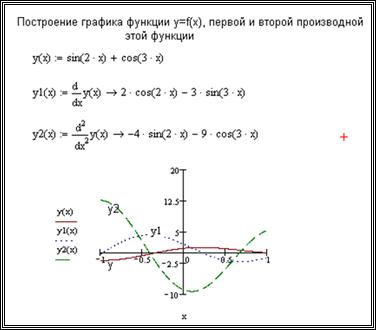
8.5.3. Построение графика касательной и нормали к кривой y = f(x)

Надо построить график касательной и нормали к кривой y = f(x) в точке с абсциссой a. Для этого необходимо найти первую производную функции y = f(x).

Если функция y = f(x) в точке a имеет конечную производную, то уравнение касательной имеет вид:

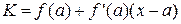
Если f’(a) = ¥, то уравнение касательной имеет вид: x = a.

Если f’(a) ¹ 0, то уравнение нормали имеет вид:

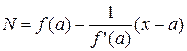
Если f’(a) = 0, то уравнение нормали имеет вид: x = a.

Пример решения данной задачи приведен на рис.8.29. Для правильного представления нормали масштабы по осям должны быть равны.

Рисунок 8.29 — График касательной и нормали к кривой в заданной точке

Эта тема принадлежит разделу:

Лекция 8

Еще одна новинка системы mathcad отсутствующая в предшествующих версиях.. применение новой функции createspace..

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Построение прямой, проходящей через две заданные точки

Видео:Уравнение прямой по двум точкамСкачать

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Лекция 8
графические возможности системы Mathcad Шаблоны для построения графиков. Двухмерные графики. Трехмерные графики. Специальная графика. Построение график

Графики в декартовой системе координат
Для построения графика в декартовой системе координат необходимо: 1. ввести выражение, описывающее некоторую функцию; 2. вывести шаблон X-Y Plot с

Форматирование двухмерных графиков
Подменю Graph меню Format (график) задает формат графиков. Для изменения формата уже построенного графика необходимо его выделить. Выделен

Трассировка и масштабирование
Еще одной возможностью при работе с двухмерными графиками является применение специального графического курсора в виде двух пунктирных линий, пересекающих все окно графика. Они поя

Графики в полярной системе координат
В полярной системе координат каждая точка задается углом fi и модулем радиус-вектора r(fi). График функции обычно строится в виде линии, которую описывает конец радиус-вектора при и

Построение поверхностей по матрице аппликат их точек
До появления Mathcad версии 2000 при построении графика поверхности, представленной функцией z(x, у) двух переменных, приходилось предварительно определять матрицу М аппликат (высот z) ее т

Построение контурных графиков поверхности
Линией уровня функции двух переменных x и y называется геометрическое место точек в плоскости xOy, в которых функция принимает одно и то же значение. Рассматривая линии уровня функции двух

Построение графика поверхности в виде гистограммы
Весьма распространенной формой представления поверхностей является также представление ее рядом трехмерных столбиков, высота которых определяется значением координаты z(x, y). Подобные гра

Построение точечного графика поверхности
Нередко поверхности представляют в виде находящихся в трехмерном пространстве точек, кружочков или иных фигур. Точечные графики позволяют построить произвольную совокупность точек в

Построение векторного графика поверхности
Еще один вид представления поверхности — векторное представление. Оно задается построением коротких стрелочек — векторов. Стрелки обращены острием в сторону нарастания высоты поверх

Применение Мастера построения трехмерных графиков
Форматирование трехмерных графиков в Mathcad 2000 довольно сложный процесс, поскольку число применяемых для этого параметров достигает многих десятков. Для облегчения задания трехмерных граф

Оперативная смена типа графика
Mathcad предусматривает возможность оперативной смены типа графика, отображающего какую-то поверхность. Для этого достаточно вывести на экран окно форматирования, введя в область графика указатель

Трехмерный график типа Patch Plot
Существует возможность построения еще одного типа графика — Patch Plot. Такой команды нет в подменю Graph меню Insert, но соответствующий переключ

Надписи на переднем и заднем плане
Форматирование графиков предусматривает вывод титульной надписи сверху или снизу графиков, а также надписей по осям. Однако такой вид форматирования имеет серьезные недостатки — размер надписей огр

CreateMesh(F, s0, s1, t0, t1, sgrid, tgrid, fmap)
Эта функция возвращает массив из трех матриц, представляющих координаты переменных x, y и z для функции F, определенной в векторной параметрической форме в качестве параметров sgrid и tgrid. Параме

Построение объемных фигур с помощью функции Polyhedron
В Mathcad 2000 Professional появилась новая функция для построения объемных фигур полиэдров: Polyhedron(“name”), где name — имя фигу

CreateSpace(F, t0, t1, tgrid, tmap)
Эта функция отличается oт функции CreateMesh только тем, что заданная в векторном виде функция F задается как функция одной переменной tgrid, причем параметры t0 и t1 устанавливают

Построение графика касательной к кривой, заданной параметрически
Зависимость y от x задается посредством параметра t: x =f(t), y = g(t). Надо построить касательную к кривой в точке A, соответствующей з

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Осваиваем Mathcad (стр. 10 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10

СПРАВОЧНИК КОМАНД И КОНСТРУКТОВ, ИСПОЛЬЗУЕМЫХ ДЛЯ ПРОГРАММИРОВАНИЯ В MATHCAD

1. Команды MathCAD НЕЛЬЗЯ набирать литерами. Их можно либо вводить из окошка «Программирование» (меню View – Toolbars– Programming, Вид – Инструменты – Программирование), либо использовать сочетания клавиш (это быстрее). Сочетания клавиш видны в окошке программирования в форме подсказок, см. рис. П 2.1. Если Вам не приходится программировать часто, запоминать сочетания клавиш нецелесообразно.

Рис. П2.1. Команды и операторы программирования.

2. Зоны охвата программных конструктов (for…, while…, if…) ограничиваются линиями, которые придают программе вид легко читаемой структуры (рис. П 2.2). Линия вводится командой Add Line (добавить линию) или клавишей «закрывающая квадратная скобка». Часто такие линии формирует сам MathCAD. Пример структуры программы:

Рис. П2.2. Структура программы. Линии выделяют зоны действия конструктов.

3. Все MathCAD-программы строятся как программы-функции. Переменные внутри программы являются локальными (действуют только в пределах программы). В конце программы приводится либо скалярная переменная, либо вектор, либо матрица, которые возвращает функция. Например, программа на рис. П 2.2 возвращает вектор из двух значений, которым внутри программы присвоены значения max и number_max.

Команды, конструкты и операторы с примерами их использования.

Оператор присваивания (стрелка справа налево). Пример:

Согласно этому оператору ЭВМ проводит следующие действия:

— Формирует константу 0;

— Находит в основной памяти свободную ячейку;

— Присваивает этой ячейке имя (идентификатор) number_max;

— Заносит в эту ячейку константу 0.

Оператор читается так: ПРИСВОИТЬ значение НУЛЬ переменной с ИДЕНТИФИКАТОРОМ number_max.

Простой оператор if (ЕСЛИ) и otherwise (В ОСТАЛЬНЫХ СЛУЧАЯХ). Пример:

Программа возвращает No, если s = 0. В других случаях (т. е. если s ¹ 0) функция возвращает Yes.

Виды условий: равно (жирный знак равенства + ), не равно ( + ), больше, меньше, больше или равно ( + ), меньше или равно ( + ) или сочетания этих условий через логические функции ИЛИ (обозначается знаком +), И (обозначается знаком умножения, *). Пример:

Программа возвращает No, если [ s = 0 ИЛИ s не равно 5] И [s не равно April]. Во всех других случаях программа возвращает Yes.

Сложный оператор (конструкт) if (ЕСЛИ). Содержит последовательность команд, охваченных действием оператора. Для ввода линии, ограничивающей зону действия, нужно установить курсор в левый слот и ввести команду Add Line (можно клавишей «открывающая квадратная скобка»). Пример приведен слева.

Если g = 4, то функция возвратит:

Если g не равно 4, то функция возвратит, например,

Конструкт for (ДЛЯ КАЖДОГО…). Конструкт for предназначен для повторяющихся (циклических) вычислений. Пример: найти сумму всех элементов массива M. Пусть в этом массиве хранятся следующие значения:

Проследим, как работает программа с циклом for и массивом M.

1. До начала цикла sum = 0.

2. Номер последнего элемента n = 6 –1 = 5

a. Формула внутри цикла читается «по-еврейски» – справа налево. Вначале в процессор поступает значение Mj с j = 0, т. е. нулевой элемент 2.2. Затем на другой регистр процессора вызывается ячейка с идентификатором sum (в ней нуль). Затем процессор складывает оба числа (2.2 + 0) = 2.2 и отсылает в ячейку памяти с идентификатором sum. Теперь там число 2.2.

b. Оператор for увеличивает номер цикла на 1 (получается j = 1) и сравнивает c n (равно 5). Поскольку номер цикла меньше 5, нужен еще один цикл с j = 1.

a. Вначале в процессор поступает значение Mj с j = 1, т. е. первый элемент 1.9. Затем на другой регистр процессора вызывается ячейка с идентификатором sum (в ней 2.2). Затем процессор складывает оба числа (1.9 + 2.2 ) = 4.1 и отсылает в ячейку памяти с идентификатором sum. Теперь там число 4.1.

b. Оператор for увеличивает номер цикла на 1 (получается j = 2) и сравнивает c n (равно 5). Поскольку номер цикла меньше 5, нужен еще один цикл с j = 2.

a. Вначале в процессор поступает значение Mj с j = 2, т. е. второй элемент 0.6. Затем на другой регистр процессора вызывается ячейка с идентификатором sum (в ней 4.1). Затем процессор складывает оба числа (0.6 + 4.1 ) = 4.7 и отсылает в ячейку памяти с идентификатором sum. Теперь там число 4.7.

b. Оператор for увеличивает номер цикла на 1 (получается j = 3) и сравнивает c n (равно 5). Поскольку номер цикла меньше 5, нужен еще один цикл с j = 3.

a. Вначале в процессор поступает значение Mj с j = 3, т. е. третий элемент 2.3. Затем на другой регистр процессора вызывается ячейка с идентификатором sum (в ней 4.7). Затем процессор складывает оба числа (2.3 + 4.7 ) = 7.0 и отсылает в ячейку памяти с идентификатором sum. Теперь там число 7.0.

b. Оператор for увеличивает номер цикла на 1 (получается j = 4) и сравнивает c n (равно 5). Поскольку номер цикла меньше 5, нужен еще один цикл с j = 4.

a. Вначале в процессор поступает значение Mj с j = 4, т. е. четвертый элемент 2.5. Затем на другой регистр процессора вызывается ячейка с идентификатором sum (в ней 7.0). Затем процессор складывает оба числа (7.0 + 2.5 ) = 9.5 и отсылает в ячейку памяти с идентификатором sum. Теперь там число 9.5.

b. Оператор for увеличивает номер цикла на 1 (получается j = 5) и сравнивает c n (равно 5). Поскольку номер цикла равен 5, нужен еще один (последний!) цикл с j = 5.

a. Вначале в процессор поступает значение Mj с j = 5, т. е. пятый элемент 2.1. Затем на другой регистр процессора вызывается ячейка с идентификатором sum (в ней 9.5). Затем процессор складывает оба числа (9.5 + 2.1 ) = 11.6 и отсылает в ячейку памяти с идентификатором sum. Теперь там число 11.6.

b. Оператор for увеличивает номер цикла на 1 (получается j = 6) и сравнивает c n (равно 5). Поскольку номер цикла БОЛЬШЕ 5, циклы прекращаются, и программа возвращает число из ячейки sum (там накопилась сумма всех элементов массива 11.6).

СПРАВОЧНИК ФОРМУЛ, НЕОБХОДИМЫХ ДЛЯ ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ИЗ ЧАСТИ 4

Плоскость, проходящая через три точки M0(x0, y0, z0), M1(x1, y1, z1) и M2(x2, y2, z2), не лежащие на одной прямой. Уравнение плоскости, определяющее ее координаты (x, y, z), получается, если приравнять нулю определитель матрицы P (если определитель равен нулю, то это является признаком того, что все три точки лежат на одной прямой. В этом случае существует бесконечное число плоскостей («пучок плоскостей»), проходящих через одну прямую):

Обозначим det(P) определитель матрицы P. Уравнение плоскости: det(P) = 0. Раскрывая определитель, выразим одну из координат (обычно z) через две другие: z = f(x, y). Получим вектор Plane (x, y) координат для построения плоскости:

Plane(x,y) =

Плоскость, проходящая через данную точку параллельно другой плоскости. Пусть задано уравнение плоскости A×x + B×y + C×z + D = 0 и имеется точка с координатами M1(x1, y1, z1), не лежащая на заданной плоскости. Тогда уравнение плоскости, проходящей через эту точку параллельно заданной плоскости, имеет вид: A×(x—x1) + B×(y—y1) + C×(z—z1) = 0. Из этого уравнения нужно выразить одну из координат (обычно z) через две другие: z = f(x, y) и сформировать вектор Plane (x, y) координат для построения плоскости.

Плоскость, параллельная координатной плоскости и расположенная на заданной высоте h. Вектор Plane (x, y) координат для построения плоскости получается так: x и y могут быть любыми, а координата z должна быть для всей плоскости одной и той же (равной заданной высоте h).

Plane(x,y) =

Плоскость, проходящая через две точки перпендикулярно к данной плоскости. Пусть задано уравнение плоскости A×x + B×y + C×z +D = 0 и две точки (возможно, но не обязательно лежащие на ней). Заданы координаты этих точек M0(x0, y0, z0) и M1(x1, y1, z1). Уравнение, определяющее координаты точек (x, y, z) искомой плоскости, получим, приравнивая нулю определитель матрицы Q:

Координаты точек плоскости находятся из уравнения det(Q) = 0.

2. Прямая линия в пространстве

Вектор координат (X, Y) для построения прямой находится так:

а) назначаем одну из координат свободной (обычно X);

б) из уравнения выразим Y = f1(X);

в) из уравнения выразим Z = f2(X).

Получим координаты для построения линии:

Если нужно показать только отрезок между двумя точками, то следует указать пределы изменения аргументов: x0 £ X £ x1, y0 £ Y £ y1.

Точка пересечения прямой и плоскости находится при решении системы уравнений, описывающей прямую и плоскость. Например, если прямая строится так, чтобы она проходила через две точки с координатами M0(x0, y0, z0) и M1(x1, y1, z1), не лежащие на заданной плоскости A×x + B×y + C×z + D = 0, то координаты (x, y, z) точки пересечения находятся из системы уравнений:

Эта система уравнений может иметь одно решение (точка пересечения единственна), бесконечно много решений (прямая линия лежит на плоскости) и ни одного решения (прямая проходит параллельно плоскости).

При заданном радиусе основания цилиндра R и высоте H положение точки M(j, h) на боковой поверхности цилиндра определяется углом j к оси абсцисс и высотой h над координатной плоскостью XOY.

Вектор Cylinder(j,h) координат для построения цилиндра:

Диапазон изменения аргументов для построения «целого» цилиндра: 0 £ h £ H, 0 £ j £ 2×p. Для построения части цилиндра нужно задать часть угла 2×p, например: 0.5×p £ j £ p.

При заданном радиусе основания конуса R и высоте H положение точки M(h, x) на боковой поверхности цилиндра определяется углом при вершине j (зависящим от соотношения высоты и радиуса основания) и высотой h над координатной плоскостью XOY.

Тангенс угла j при вершине конуса равен:

Вектор Cone(h, x) координат для построения чертежа конуса:

Диапазон изменения аргументов для построения «целого» конуса: 0 £ h £ H, 0 £ x £ 2×p. Для построения части конуса нужно задать часть угла 2×p, например: 0.5×p £ x £ p.

Примечание: функция «тангенс» в MathCAD называется не tg( ), а tan( ).

ЧАСТЬ 1. ПЕРВОЕ ЗНАКОМСТВО С MATHCAD ……………….

Введение. Общие правила работы в среде Mathcad ……………