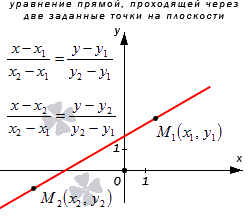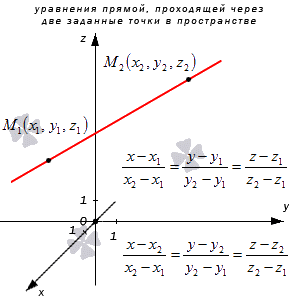Уравнение прямой по 2 точкам в трехмерном пространстве (3 видео)

Уравнение прямой, которая проходит через две заданные точки: примеры, решения

Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.

Содержание

Уравнение прямой, проходящей через две заданные точки на плоскости
Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве
Уравнение прямой проходящей через две точки
Прямая в пространстве – виды уравнения прямой в пространстве
Параметрическое и каноническое уравнение прямой в пространстве
Уравнение прямой в пространстве, которая проходит через две заданные точки
Общее уравнение прямой – переход к каноническому уравнению
Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых
Примеры решения задач
🔥 Видео

Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Уравнение прямой, проходящей через две заданные точки на плоскости

Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.

Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.

Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a , проходящей через две несовпадающие точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , находящиеся в декартовой системе координат.

В каноническом уравнении прямой на плоскости, имеющего вид x — x 1 a x = y — y 1 a y , задается прямоугольная система координат О х у с прямой, которая пересекается с ней в точке с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) .

Необходимо составить каноническое уравнение прямой a , которая пройдет через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) .

Прямая а имеет направляющий вектор M 1 M 2 → с координатами ( x 2 — x 1 , y 2 — y 1 ) , так как пересекает точки М 1 и М 2 . Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 ) и координатами лежащих на них точках M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 .

Рассмотрим рисунок, приведенный ниже.

Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ .

Рассмотрим подробней на решении нескольких примеров.

Записать уравнение прямой, проходящей через 2 заданные точки с координатами M 1 — 5 , 2 3 , M 2 1 , — 1 6 .

Каноническим уравнением для прямой, пересекающейся в двух точках с координатами x 1 , y 1 и x 2 , y 2 принимает вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . По условию задачи имеем, что x 1 = — 5 , y 1 = 2 3 , x 2 = 1 , y 2 = — 1 6 . Необходимо подставить числовые значения в уравнение x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . Отсюда получим, что каноническое уравнение примет вид x — ( — 5 ) 1 — ( — 5 ) = y — 2 3 — 1 6 — 2 3 ⇔ x + 5 6 = y — 2 3 — 5 6 .

Ответ: x + 5 6 = y — 2 3 — 5 6 .

При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.

Составить общее уравнение прямой, проходящей через точки с координатами M 1 ( 1 , 1 ) и M 2 ( 4 , 2 ) в системе координат О х у .

Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки. Получим уравнение вида x — 1 4 — 1 = y — 1 2 — 1 ⇔ x — 1 3 = y — 1 1 .

Приведем каноническое уравнение к искомому виду, тогда получим:

x — 1 3 = y — 1 1 ⇔ 1 · x — 1 = 3 · y — 1 ⇔ x — 3 y + 2 = 0

Ответ: x — 3 y + 2 = 0 .

Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y = k x + b . Если необходимо найти значение углового коэффициента k и числа b , при которых уравнение y = k x + b определяет линию в системе О х у , которая проходит через точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , где x 1 ≠ x 2 . Когда x 1 = x 2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М 1 М 2 определена общим неполным уравнением вида x — x 1 = 0 .

Потому как точки М 1 и М 2 находятся на прямой, тогда их координаты удовлетворяют уравнению y 1 = k x 1 + b и y 2 = k x 2 + b . Следует решить систему уравнений y 1 = k x 1 + b y 2 = k x 2 + b относительно k и b .

Для этого найдем k = y 2 — y 1 x 2 — x 1 b = y 1 — y 2 — y 1 x 2 — x 1 · x 1 или k = y 2 — y 1 x 2 — x 1 b = y 2 — y 2 — y 1 x 2 — x 1 · x 2 .

С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 1 или y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 2 .

Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.

Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами M 2 ( 2 , 1 ) и y = k x + b .

Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид y = k x + b . Коэффициенты k и b должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами M 1 ( — 7 , — 5 ) и M 2 ( 2 , 1 ) .

Точки М 1 и М 2 располагаются на прямой, тогда их координаты должны обращать уравнение y = k x + b верное равенство. Отсюда получаем, что — 5 = k · ( — 7 ) + b и 1 = k · 2 + b . Объединим уравнение в систему — 5 = k · — 7 + b 1 = k · 2 + b и решим.

При подстановке получаем, что

— 5 = k · — 7 + b 1 = k · 2 + b ⇔ b = — 5 + 7 k 2 k + b = 1 ⇔ b = — 5 + 7 k 2 k — 5 + 7 k = 1 ⇔ ⇔ b = — 5 + 7 k k = 2 3 ⇔ b = — 5 + 7 · 2 3 k = 2 3 ⇔ b = — 1 3 k = 2 3

Теперь значения k = 2 3 и b = — 1 3 подвергаются подстановке в уравнение y = k x + b . Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид y = 2 3 x — 1 3 .

Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.

Запишем каноническое уравнение прямой, проходящей через M 2 ( 2 , 1 ) и M 1 ( — 7 , — 5 ) , имеющее вид x — ( — 7 ) 2 — ( — 7 ) = y — ( — 5 ) 1 — ( — 5 ) ⇔ x + 7 9 = y + 5 6 .

Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: x + 7 9 = y + 5 6 ⇔ 6 · ( x + 7 ) = 9 · ( y + 5 ) ⇔ y = 2 3 x — 1 3 .

Ответ: y = 2 3 x — 1 3 .

Видео:Уравнение прямой по двум точкамСкачать

Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве

Если в трехмерном пространстве имеется прямоугольная система координат О х у z с двумя заданными несовпадающими точками с координатами M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , проходящая через них прямая M 1 M 2 , необходимо получить уравнение этой прямой.

Имеем, что канонические уравнения вида x — x 1 a x = y — y 1 a y = z — z 1 a z и параметрические вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ способны задать линию в системе координат О х у z , проходящую через точки, имеющие координаты ( x 1 , y 1 , z 1 ) с направляющим вектором a → = ( a x , a y , a z ) .

Прямая M 1 M 2 имеет направляющий вектор вида M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) , где прямая проходит через точку M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , отсюда каноническое уравнение может быть вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1 , в свою очередь параметрические x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ z = z 1 + ( z 2 — z 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ z = z 2 + ( z 2 — z 1 ) · λ .

Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.

Написать уравнение прямой, определенной в прямоугольной системе координат О х у z трехмерного пространства, проходящей через заданные две точки с координатами M 1 ( 2 , — 3 , 0 ) и M 2 ( 1 , — 3 , — 5 ) .

Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 .

По условию имеем, что x 1 = 2 , y 1 = — 3 , z 1 = 0 , x 2 = 1 , y 2 = — 3 , z 2 = — 5 . Отсюда следует, что необходимые уравнения запишутся таким образом:

x — 2 1 — 2 = y — ( — 3 ) — 3 — ( — 3 ) = z — 0 — 5 — 0 ⇔ x — 2 — 1 = y + 3 0 = z — 5

Ответ: x — 2 — 1 = y + 3 0 = z — 5 .

Видео:§51 Уравнение прямой в пространстве, проходящей через две точкиСкачать

Уравнение прямой проходящей через две точки

Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.

Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнения прямой, проходящей через две точки могут быть следующих видов:

каноническое уравнение,
параметрическое уравнение,
общее уравнение прямой,
уравнение прямой с угловым коэффициентом,
уравнение прямой в полярных координатах и другие.

Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Прямая в пространстве – виды уравнения прямой в пространстве

Прямая в пространстве – это линия, которая проходит от одной точки к другой, а также за пределы этих точек в бесконечность. Есть несколько видов уравнения прямой в пространстве: каноническое, параметрическое, угол между двумя прямыми в пространстве и т. д. Про это расскажем в данной статье и для наглядности предоставим несколько примеров.

Видео:Видеоурок "Уравнение прямой, проходящей через две точки"Скачать

Параметрическое и каноническое уравнение прямой в пространстве

Параметрическое и каноническое уравнение прямой рассматривается практически так, как и для прямой на плоскости. Значит, нужно составить уравнение прямой , которая проходит через данную точку параллельно направляющему вектору .

Пусть, – произвольная точка прямой, тогда векторы и коллинеарные, а это значит, что координаты их пропорциональны, поэтому получаем:

это и есть канонические уравнения прямой.

Приравнивая каждую из дробей (1) к параметру , запишем параметрические уравнения прямой:

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение прямой в пространстве, которая проходит через две заданные точки

Уравнение прямой в пространстве – тема очень лёгкая, так как здесь самое важное – знать нужную формулу. Тогда легко можно решить любую задачу.

Итак, через две точки и можно не только геометрично провести линию, но и сложить её уравнения.

За направляющий вектор возьмём , тогда по формуле (1) у нас получается:

уравнение прямой в пространстве, которые проходят через две заданные точки.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Общее уравнение прямой – переход к каноническому уравнению

Объяснение про общее уравнение прямой начнём с прямой, которая задана двумя плоскостями, что пересекаются по этой прямой.

Пусть известны их уравнения:

Тогда система (4) называется общим уравнением прямой.

Чтобы перейти к каноническим уравнениям вида (1), необходимо найти вектор и точку этой прямой.

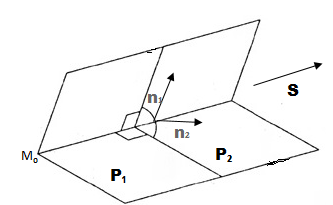
Точку находим, как один из решений системы (4). Например, положив в (4) находим , тогда и точку . Направляющий вектор , который параллелен к каждой из плоскостей и и перпендикулярен к их нормальным векторам и , то есть , . (см. рис. 1). Поэтому вектор можно найти при помощи векторного произведения и

= x =

Найдены координаты и подставим в каноническое уравнение (1).

Например, от общих уравнений прямой:

Перейдём к каноническим, положив в системе (при нём относительно больше коэффициенты). найдём . Нормальные векторы и . Тогда направляющий вектор

x = ,

и канонические уравнения станут:

Видео:11. Прямая в пространстве и ее уравненияСкачать

Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых

Угол между двумя прямыми :

равен углу между их направляющими векторами и , поэтому

Условия параллельности и перпендикулярности прямых соответственно запишутся:

и .

Видео:Видеоурок "Уравнение плоскости по трем точкам"Скачать

Примеры решения задач

Давайте рассмотрим первый пример, где можно двумя способами построить прямую:

Задача

При точке и направляющем векторе необходимо:

составить каноническое уравнение прямой;
построить эту прямую.

Решение

1) По формуле (1) запишем каноническое уравнение прямой :

= .

2) Рассмотрим два способа построения прямой .

Первый способ

В системе координат строим вектор и точку и проводим через точку прямую параллельную вектору .

Второй способ

По формуле (2) запишем каноническое уравнение прямой в параметрическом виде:

На рисунке видно, что при произвольных значениях из системы находим координаты соответствующих точек, которые принадлежат прямой . Так при находим координаты . Через две точки и проводим прямую .

Очевидно, что найти острый угол между прямыми совершенно не сложно при знании темы и определённых формул. Давайте разберём такой пример:

Задача

Найти острый угол между прямыми:

Решение

По формуле (7) получаем:

= = =

Так как , тогда угол тупой, , а острый угол .

Ответ

Рассмотрим последний пример, где нужно составить уравнение. Здесь, как и в каждой задаче, важно знать и понимать, какой формулой нужно воспользоваться.

Задача

Составить уравнение прямой , которая проходит через точку и параллельна прямой .

Решение

От параметрического уравнения переходим к каноническому При условии параллельности прямых то есть направляющим вектором новой прямой может служить известный вектор и по формуле (1) у нас получается: