В этой статье всесторонне раскрыта тема «параллельность прямой и плоскости». Сначала дано определение параллельных прямой и плоскости, приведена графическая иллюстрация и пример. Далее сформулирован признак параллельности прямой и плоскости, а также озвучены необходимые и достаточные условия параллельности прямой и плоскости. В заключении приведены развернутые решения задач, в которых доказывается параллельность прямой и плоскости.
Навигация по странице.
- Параллельные прямая и плоскость – основные сведения.
- Параллельность прямой и плоскости — признак и условия параллельности.
- Уравнение плоскости, проходящей через данную прямую параллельно другой прямой онлайн
- Предупреждение
- Уравнение плоскости, проходящей через данную прямую параллельно другой прямой − теория, примеры и решения
- Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости
- Параллельные прямые и плоскость – основные сведения
- Параллельность прямой и плоскости – признак и условия параллельности
- 💡 Видео
Видео:12. Уравнения прямой в пространстве Решение задачСкачать
Параллельные прямая и плоскость – основные сведения.
Начнем с определения параллельных прямой и плоскости.
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Для обозначения параллельности используется символ «
». То есть, если прямая a и плоскость 
параллельны, то можно кратко записать a .
Заметим, что выражения «прямая a и плоскость параллельны», «прямая a параллельна плоскости » и «плоскость параллельна прямой a » одинаково употребимы.
В качестве примера параллельных прямой и плоскости приведем натянутую гитарную струну и плоскость грифа этой гитары.
Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать
Параллельность прямой и плоскости — признак и условия параллельности.
Параллельность прямой и плоскости далеко не всегда является очевидным фактом. Другими словами, параллельность прямой и плоскости приходится доказывать. Существует достаточное условие, выполнение которого гарантирует параллельность прямой и плоскости. Это условие называют признаком параллельности прямой и плоскости. Прежде чем ознакомиться с формулировкой этого признака, рекомендуем повторить определение параллельных прямых.
Если прямая a , не лежащая в плоскости , параллельна некоторой прямой b , которая лежит в плоскости , то прямая a параллельна плоскости .
Озвучим еще одну теорему, которую можно использовать для установления параллельности прямой и плоскости.
Если одна из двух параллельных прямых параллельна некоторой плоскости, то вторая прямая либо также параллельна этой плоскости, либо лежит в ней.
Доказательство признака параллельности прямой и плоскости и доказательство озвученной теоремы приводятся в учебнике геометрии за 10 — 11 классы, который указан в конце статьи в списке рекомендованной литературы.
Определение направляющего вектора прямой и определение нормального вектора плоскости позволяют записать необходимое и достаточное условие параллельности прямой и плоскости.
Для параллельности прямой a , не лежащей в плоскости , и плоскости необходимо и достаточно, чтобы направляющий вектор прямой a был перпендикулярен нормальному вектору плоскости .
Это условие удобно использовать для доказательства параллельности прямой и плоскости, которые заданы в прямоугольной системе координат в трехмерном пространстве некоторыми уравнениями.
Пусть прямую a в прямоугольной системе координат Oxyz задают канонические уравнения прямой в пространстве вида 
или параметрические уравнения прямой в пространстве вида 
, а плоскости соответствует общее уравнение плоскости 
. Тогда 
— направляющий вектор прямой a , а 
— нормальный вектор плоскости . Для перпендикулярности векторов и необходимо и достаточно, чтобы скалярное произведение 
равнялось нулю (об этом написано в статье условие перпендикулярности двух векторов).
Следовательно, необходимое и достаточное условие параллельности прямой a и плоскости ( a не лежит в плоскости ) примет вид 
, где — направляющий вектор прямой a , — нормальный вектор плоскости .
Разберем решения нескольких примеров.
Являются ли прямая 
и плоскость 
параллельными?
Заданная прямая не лежит в плоскости, так как координаты точки прямой 
не удовлетворяют уравнению плоскости: 
. Проверим выполнение необходимого и достаточного условия параллельности прямой и плоскости. Очевидно, 
— направляющий вектор прямой , 
— нормальный вектор плоскости . Вычислим скалярное произведение векторов 
и 
: 
. Таким образом, векторы и перпендикулярны. Следовательно, заданные прямая и плоскость параллельны.
да, прямая и плоскость параллельны.
Параллельна ли прямая АВ координатной плоскости Oyz , если 
.
Точка 
не лежит в координатной плоскости Oyz , так как абсцисса этой точки отлична от нуля.
Нормальным вектором плоскости Oyz является вектор 
. В качестве направляющего вектора прямой AB возьмем вектор 
. Координаты точек начала и конца вектора позволяют вычислить координаты этого вектора, тогда 
. Проверим выполнение необходимого и достаточного условия перпендикулярности векторов и : 
. Следовательно, прямая AB и координатная плоскость Oyz не параллельны.
нет, не параллельны.
Разобранное условие не совсем удобно для доказательства параллельности прямой a и плоскости , так как отдельно приходится проверять, что прямая a не лежит в плоскости . Поэтому, доказывать параллельность прямой a и плоскости удобнее с помощью следующего необходимого и достаточного условия.
Пусть прямая a задана уравнениями двух пересекающихся плоскостей 
,
а плоскость — общим уравнением плоскости 
.
Для параллельности прямой a и плоскости необходимо и достаточно, чтобы система линейных уравнений вида 
не имела решений.
Действительно, если прямая a параллельна плоскости , то они по определению не имеют общих точек. Следовательно, не существует ни одной точки в прямоугольной системе координат Oxyz , координаты которой удовлетворяли бы одновременно и уравнениям прямой и уравнению плоскости . Значит, система уравнений вида несовместна.
И обратно: если система уравнений вида не имеет решений, то не существует ни одной точки в прямоугольной системе координат Oxyz , координаты которой удовлетворяли бы одновременно всем уравнениям системы. Тогда, не существует точки, координаты которой одновременно удовлетворяют и уравнениям прямой и уравнению плоскости . Следовательно, прямая a и плоскость не имеют общих точек, то есть, они параллельны.
В свою очередь система уравнений не имеет решений, когда ранг основной матрицы системы меньше ранга расширенной матрицы (это следует из теоремы Кронекера-Капелли, при необходимости смотрите статью решение систем линейных уравнений). Несовместность этой системы уравнений можно также показать, используя метод Гаусса для решения систем линейных уравнений.
Докажите параллельность прямой 
и плоскости 
.
Перейдем от канонических уравнений прямой к уравнениям двух пересекающихся плоскостей:
Для доказательства параллельности прямой 
и плоскости покажем, что система уравнений 
не имеет решения. Воспользуемся методом Гаусса:
Действительно, система уравнений несовместна, следовательно, заданные прямая и плоскость не имеют общих точек. Этим доказана параллельность прямой и плоскости .
Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать
Уравнение плоскости, проходящей через данную прямую параллельно другой прямой онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через прямую L1 параллельно другой прямой L2 (прямые L1 и L2 не параллельны). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямых (канонический или параметрический) введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать
Уравнение плоскости, проходящей через данную прямую параллельно другой прямой − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2, которые не параллельны:
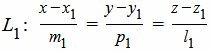 . | (1) |
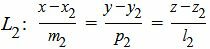 . | (2) |
Задача заключается в построении уравнения плоскости α, проходящей через прямую L1 параллельно прямой L2(Рис.1).
 |
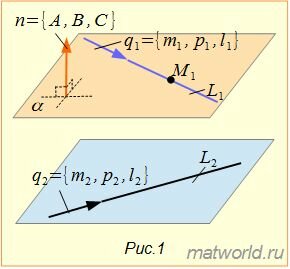Прамая L1 должна лежать на искомой плоскости α, следовательно точка M1 должна нежать на плоскости α.
Уравнение плоскости можно записать формулой
| Ax+By+Cz+D=0. | (3) |
и поскольку M1(x1, y1, z1) принадлежит этой плоскости, то справедливо следующее равенство:
| Ax1+By1+Cz1+D=0. | (4) |
Для того, чтобы плоскость α проходила через прямую L1, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q1 прямой L1, т.е. скалярное произведение этих векторов должен быть равным нулю:
| Am1+Bp1+Cl1=0 | (5) |
Для того, чтобы плоскость α была параллельна прямой L2, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q2 прямой L2, т.е. скалярное произведение этих векторов должен быть равным нулю:
| Am2+Bp2+Cl2=0 | (6) |
Таким образом мы должны решить систему трех уравнений с четыремя неизвестными (4)−(6). Представим систему линейных уравнений (4)−(6) в матричном виде:
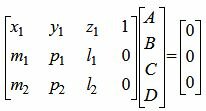 | (7) |
Решив однородную систему линейных уравнений (7) найдем частное решение. (как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн). Подставляя полученные коэффициенты A, B, C и D в уравнение (3), получим уравнение плоскости, проходящей через прямую L1 параллельно прямой L2.
Пример 1. Найти уравнение плоскости α, проходящей через прямую L1:
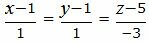 | (8) |
паралленьно другой прямой L2 :
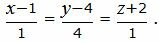 | (9) |
 |
 |
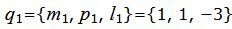Поскольку плоскость проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(1, 1, 5) и нормальный вектор плоскости n=<A, B, C> перпендикулярна направляющему вектору q1=<m1, p1, l1>= прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
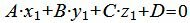 | (10) |
а условие параллельности прямой L1 и искомой плоскости α представляется следующим равенством:
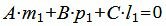 | (11) |
Так как плоскость α должна быть параллельной прямой L2, то должна выполнятся условие:
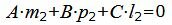 | (12) |
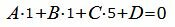 | (13) |
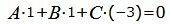 | (14) |
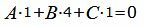 | (15) |
Представим эти уравнения в матричном виде:
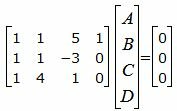 | (16) |
Решим систему линейных уравнений (16) отностительно A, B, C, D:
 | (17) |
Так как искомая плоскость проходит через точку M1 и имеет нормальный вектор n=<A, B, C>= то она может быть представлена формулой:
| Ax+By+Cz+D=0 | (18) |
Подставляя значения A,B,C,D в (17), получим:
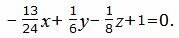 | (18) |
Уравнение плоскости можно представить более упрощенном виде, умножив на число −24:
| 13x−4y+3z−24=0 | (19) |
Ответ: Уравнение плоскости, проходящей через прямую (1) параллельно прямой (2) имеет вид (19).
Пример 2. Найти уравнение плоскости α, проходящей через прямую L1:
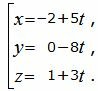 | (20) |
| q1=<m1, p1, l1>= |
| q2=<m2, p2, l2>= |
Поскольку плоскость проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(−2, 0, 1) и нормальный вектор плоскости n=<A, B, C> перпендикулярна направляющему вектору q1=<m1, p1, l1>= прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
| Ax1+By1+Cz1+D=0 | (22) |
а условие параллельности прямой L1 и искомой плоскости α представляется следующим равенством:
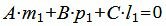| (23) |
Так как плоскость α должна быть параллельной прямой L2, то должна выполнятся условие:
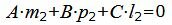| (24) |
| A(−2)+B·0+C·1+D=0, | (25) |
| A·5+B(−8)+C·3=0, | (26) |
| A·1+B·1+C·1=0, | (27) |
Представим эти уравнения в матричном виде:
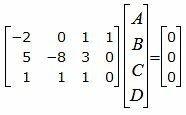 | (28) |
Решим систему линейных уравнений (28) отностительно A, B, C, D:
 | (29) |
Так как искомая плоскость проходит через точку M1 и имеет нормальный вектор n=<A, B, C>= то она может быть представлена формулой:
| Ax+By+Cz+D=0 | (30) |
Подставляя значения A,B,C,D в (30), получим:
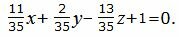 | (31) |
Уравнение плоскости можно представить более упрощенном виде, умножив на число 35:
| 11x+2y−13z+35=0 | (32) |
Ответ: Уравнение плоскости, проходящей через прямую (1) параллельно прямой (2) имеет вид (32).
Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать
Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости
Статья рассматривает понятия параллельность прямой и плоскости. Будут рассмотрены основные определения и приведены примеры. Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.
Видео:9 класс, 7 урок, Уравнение прямойСкачать
Параллельные прямые и плоскость – основные сведения
Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.
Параллельность обозначается « ∥ ». Если в задании по условию прямая a и плоскость α параллельны, тогда обозначение имеет вид a ∥ α . Рассмотрим рисунок, приведенный ниже.
Считается, что прямая a , параллельная плоскости α и плоскость α , параллельная прямой a , равнозначные, то есть прямая и плоскость параллельны друг другу в любом случае.
Видео:Уравнение плоскости через 2 точки параллельно прямойСкачать
Параллельность прямой и плоскости – признак и условия параллельности
Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.
Если заданная прямая a , не лежащая в плоскости α , параллельна прямой b , которая принадлежит плоскости α , тогда прямая a параллельна плоскости α .
Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.
Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.
Подробное доказательство рассмотрено в учебнике 10 — 11 класса по геометрии. Необходимым и достаточным условием параллельности прямой с плоскостью возможно при наличии определения направляющего вектора прямой и нормального вектора плоскости.
Для параллельности прямой a , не принадлежащей плоскости α , и данной плоскости необходимым и достаточным условием является перпендикулярность направляющего вектора прямой с нормальным вектором заданной плоскости.
Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.
Допустим, прямая а в систему координат О х у задается каноническими уравнениями прямой в пространстве , которые имеют вид x — x 1 a x = y — y 1 a y = z — z 1 a z или параметрическими уравнениями прямой в пространстве x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , плоскостью α с общими уравнениями плоскости A x + B y + C z + D = 0 .
Отсюда a → = ( a x , a y , a z ) является направляющим вектором с координатами прямой а, n → = ( A , B , C ) — нормальным вектором заданной плоскости альфа.
Чтобы доказать перпендикулярность n → = ( A , B , C ) и a → = ( a x , a y , a z ) , нужно использовать понятие скалярного произведения. То есть при произведении a → , n → = a x · A + a y · B + a z · C результат должен быть равен нулю из условия перпендикулярности векторов.
Значит, что необходимым и достаточным условием параллельности прямой и плоскости запишется так a → , n → = a x · A + a y · B + a z · C . Отсюда a → = ( a x , a y , a z ) является направляющим вектором прямой a с координатами, а n → = ( A , B , C ) — нормальным вектором плоскости α .
Определить, параллельны ли прямая x = 1 + 2 · λ y = — 2 + 3 · λ z = 2 — 4 · λ с плоскостью x + 6 y + 5 z + 4 = 0 .
Получаем, что предоставленная прямая не принадлежит плоскости, так как координаты прямой M ( 1 , — 2 , 2 ) не подходят. При подстановке получаем, что 1 + 6 · ( — 2 ) + 5 · 2 + 4 = 0 ⇔ 3 = 0 .
Необходимо проверить на выполнимость необходимое и достаточное условие параллельности прямой и плоскости. Получим, что координаты направляющего вектора прямой x = 1 + 2 · λ y = — 2 + 3 · λ z = 2 — 4 · λ имеют значения a → = ( 2 , 3 , — 4 ) .
Нормальным вектором для плоскости x + 6 y + 5 z + 4 = 0 считается n → = ( 1 , 6 , 5 ) . Перейдем к вычислению скалярного произведения векторов a → и n → . Получим, что a → , n → = 2 · 1 + 3 · 6 + ( — 4 ) · 5 = 0 .
Значит, перпендикулярность векторов a → и n → очевидна. Отсюда следует, что прямая с плоскостью являются параллельными.
Ответ: прямая с плоскостью параллельны.
Определить параллельность прямой А В в координатной плоскости О у z , когда даны координаты A ( 2 , 3 , 0 ) , B ( 4 , — 1 , — 7 ) .
По условию видно, что точка A ( 2 , 3 , 0 ) не лежит на оси О х , так как значение x не равно 0 .
Для плоскости O x z вектор с координатами i → = ( 1 , 0 , 0 ) считается нормальным вектором данной плоскости. Обозначим направляющий вектор прямой A B как A B → . Теперь при помощи координат начала и конца рассчитаем координаты вектора A B . Получим, что A B → = ( 2 , — 4 , — 7 ) . Необходимо выполнить проверку на выполнимость необходимого и достаточного условия векторов A B → = ( 2 , — 4 , — 7 ) и i → = ( 1 , 0 , 0 ) , чтобы определить их перпендикулярность.
Запишем A B → , i → = 2 · 1 + ( — 4 ) · 0 + ( — 7 ) · 0 = 2 ≠ 0 .
Отсюда следует, что прямая А В с координатной плоскостью О y z не являются параллельными.
Ответ: не параллельны.
Не всегда заданное условие способствует легкому определению доказательства параллельности прямой и плоскости. Появляется необходимость в проверке принадлежности прямой a плоскости α . Существует еще одно достаточное условие, при помощи которого доказывается параллельность.
При заданной прямой a с помощью уравнения двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 , плоскостью α — общим уравнением плоскости A x + B y + C z + D = 0 .
Необходимым и достаточным условием для параллельности прямой a и плоскости α яляется отсутствие решений системы линейных уравнений, имеющей вид A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 .
Из определения следует, что прямая a с плоскостью α не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат О х у z не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:
A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 , а также уравнению плоскости A x + B y + C z + D = 0 .
Следовательно, система уравнений, имеющая вид A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 , называется несовместной.
Верно обратное: при отсутствии решений системы A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не существует точек в О х у z , удовлетворяющих всем заданным уравнениям одновременно. Получаем, что нет такой точки с координатами, которая могла бы сразу быть решениями всех уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 и уравнения A x + B y + C z + D = 0 . Значит, имеем параллельность прямой и плоскости, так как отсутствуют их точки пересечения.
Система уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.
Доказать , что прямая x — 1 = y + 2 — 1 = z 3 параллельна плоскости 6 x — 5 y + 1 3 z — 2 3 = 0 .
Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:
x — 1 = y + 2 — 1 = z 3 ⇔ — 1 · x = — 1 · ( y + 2 ) 3 · x = — 1 · z 3 · ( y + 2 ) = — 1 · z ⇔ x — y — 2 = 0 3 x + z = 0
Чтобы доказать параллельность заданной прямой x — y — 2 = 0 3 x + z = 0 с плоскостью 6 x — 5 y + 1 3 z — 2 3 = 0 , необходимо уравнения преобразовать в систему уравнений x — y — 2 = 0 3 x + z = 0 6 x — 5 y + 1 3 z — 2 3 = 0 .
Видим, что она не решаема, значит прибегнем к методу Гаусса.
Расписав уравнения, получаем, что 1 — 1 0 2 3 0 1 0 6 — 5 1 3 2 3
1 — 1 0 2 0 3 1 — 6 0 1 1 3 — 11 1 3
1 — 1 0 2 0 3 1 — 6 0 0 0 — 9 1 3 .
Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.
Делаем вывод, что прямая x — 1 = y + 2 — 1 = z 3 и плоскость 6 x — 5 y + 1 3 z — 2 3 = 0 параллельны, так как было выполнено необходимое и достаточное условие для параллельности плоскости с заданной прямой.
Ответ: прямая и плоскость параллельны.
💡 Видео
Математика без Ху!ни. Уравнение плоскости.Скачать
Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать
Уравнение параллельной прямойСкачать
2. Уравнение плоскости примеры решения задач #1Скачать
Параллельность прямой к плоскостиСкачать
Построение параллельной плоскости на расстояние 30 мм.Скачать
10 класс, 18 урок, Теорема о прямой, перпендикулярной к плоскостиСкачать
Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать
4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать
Написать канонические и параметрические уравнения прямой в пространствеСкачать
Лекция 23. Виды уравнений прямой на плоскости.Скачать
