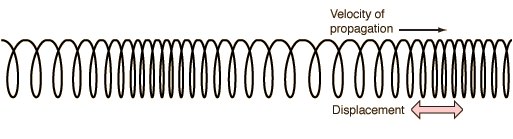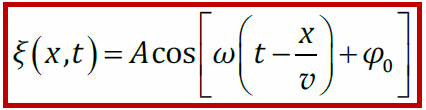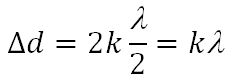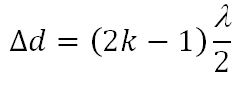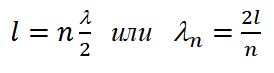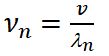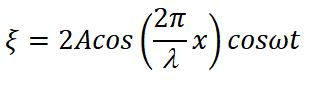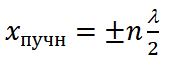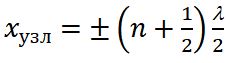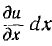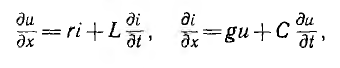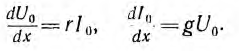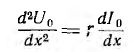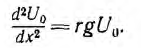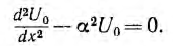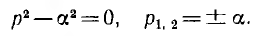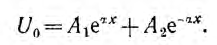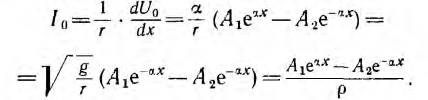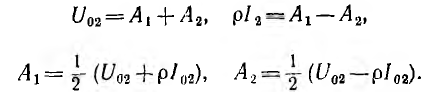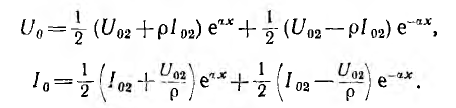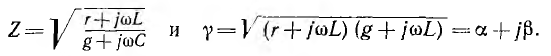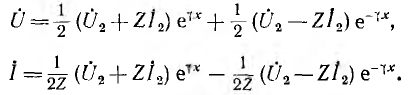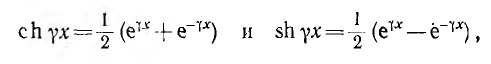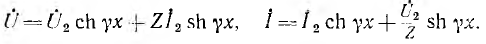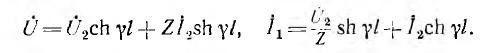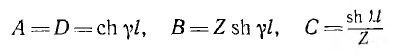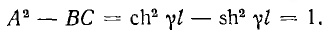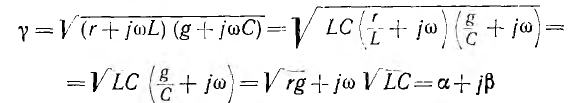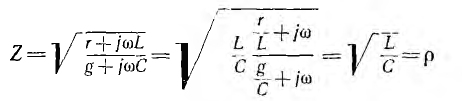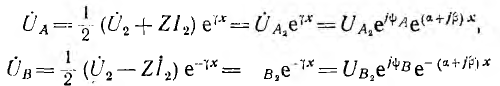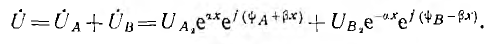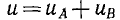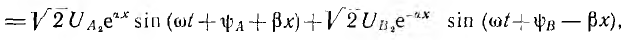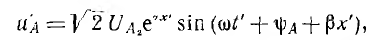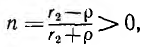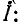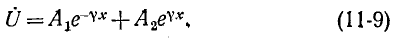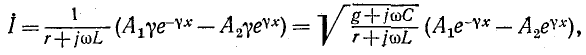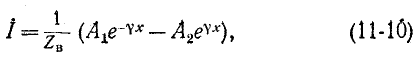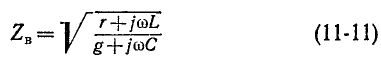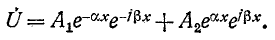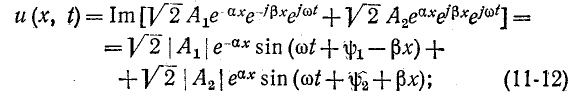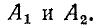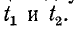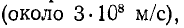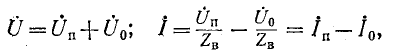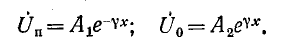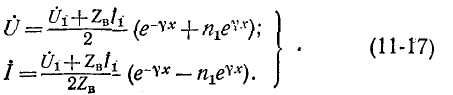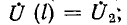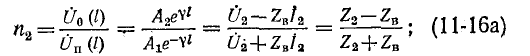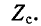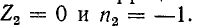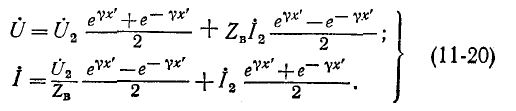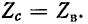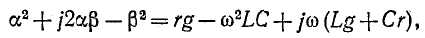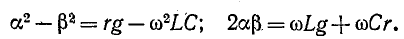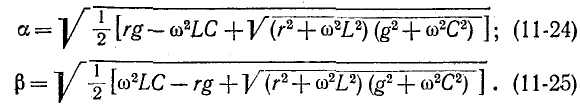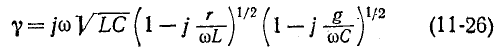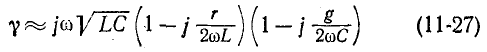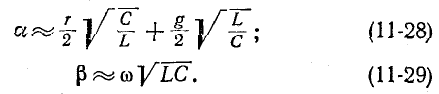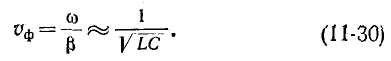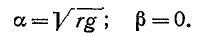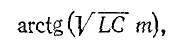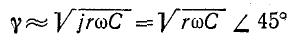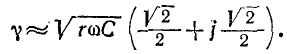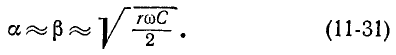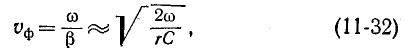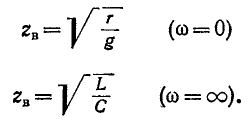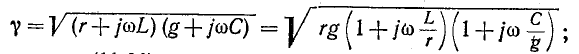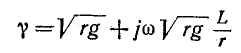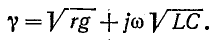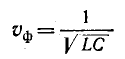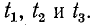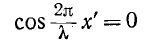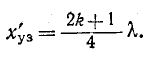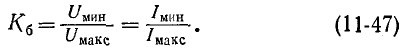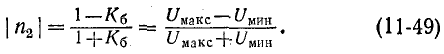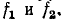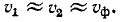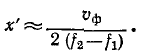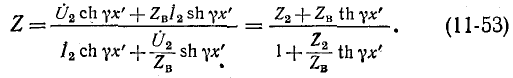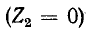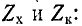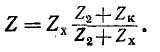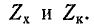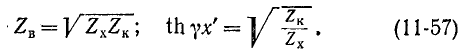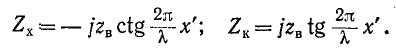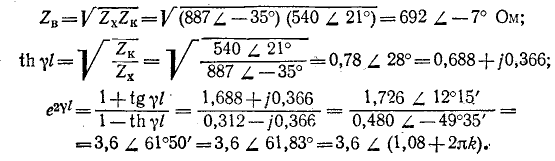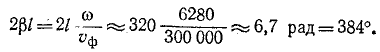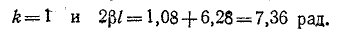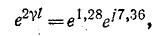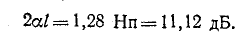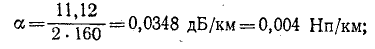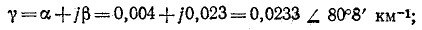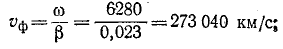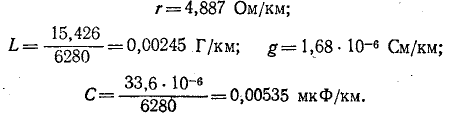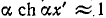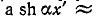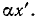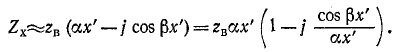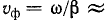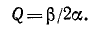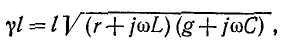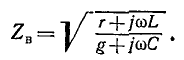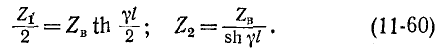Для существования волны необходим источник колебания и материальная среда или поле, в которых эта волна распространяется. Волны бывают самой разнообразной природы, но они подчиняются аналогичным закономерностям.
По физической природе различают:
упругие, звуковые, волны на поверхности жидкости
свет, радиоволны, излучения
По ориентации возмущений различают:
Смещение частиц происходит вдоль направления распространения;
могут распростаняться только в упругих средах;
необходимо наличие в среде силы упругости при сжатии;
могут распространяться в любых средах.
Смещение частиц происходит поперек направления распространения;
могут распростаняться только в упругих средах;
необходимо наличие в среде силы упругости при сдвиге;
могут распространяться только в твердых средах (и на границе двух сред).
Примеры: упругие волны в струне, волны на воде
По характеру зависимости от времени различают:
Упругие волны — механические возмещения (деформации), распространяющиеся в упругой среде. Упругая волна называется гармонической (синусоидальной), если соответствующие ей колебания среды являются гармоническими.
Бегущие волны — волны, переносящие энергию в пространстве.
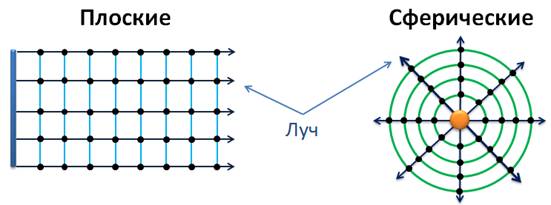
По форме волновой поверхности: плоская, сферическая, цилиндрическая волна.
Волновой фронт — геометрическое место точек, до которых дошли колебания к данному моменту времени.
Волновая поверхность — геометрическое место точек, колеблющихся в одной фазе.
Характеристики волны
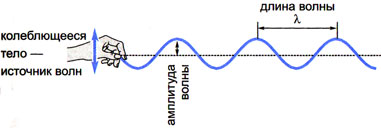
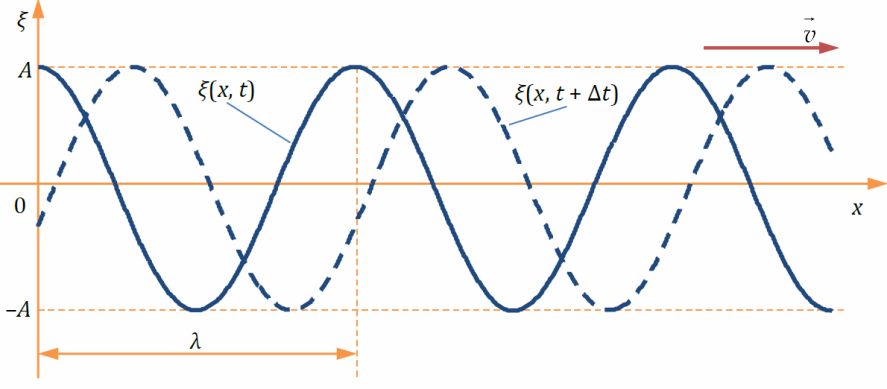
Длина волны λ — расстояние, на которое волна распространяется за время, равное периоду колебаний
Амплитуда волны А — амплитуда колебаний частиц в волне
Скорость волны v — скорость распространения возмущений в среде
Период волны Т — период колебаний
Частота волны ν — величина, обратная периоду
Уравнение бегущей волны
В процессе распространения бегущей волны возмущения среды доходят до следующих точек пространства, при этом волна переносит энергию и импульс, но не переносит вещество (частицы среды продолжают колебаться в том же месте пространства).
где v – скорость, φ0 – начальная фаза, ω – циклическая частота, A – амплитуда
Свойства механических волн
1. Отражение волн – механические волны любого происхождения обладают способностью отражаться от границы раздела двух сред. Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду.
2. Преломление волн – при распространении механических волн можно наблюдать и явление преломления: изменение направления распространения механических волн при переходе из одной среды в другую.
3. Дифракция волн – отклонение волн от прямолинейного распространения, то есть огибание ими препятствий.
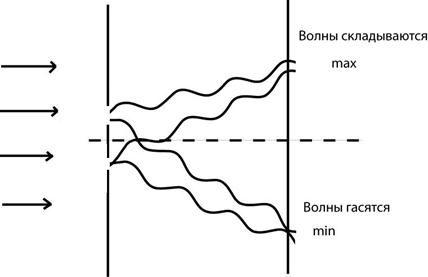
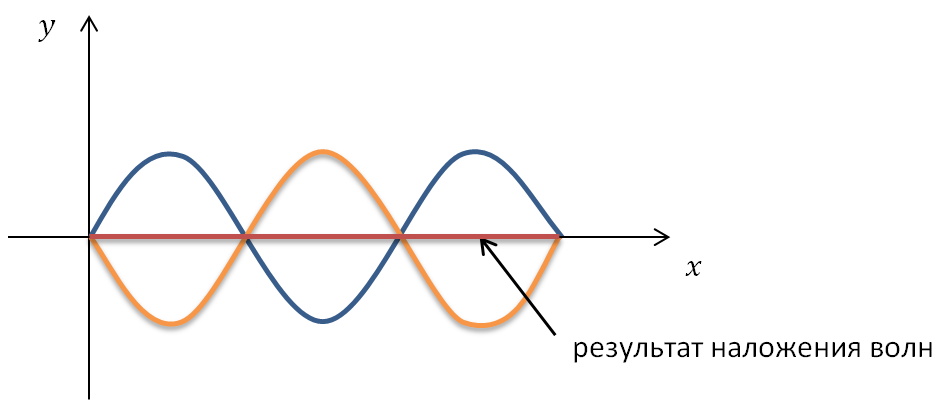
4. Интерференция волн – сложение двух волн. В пространстве, где распространяются несколько волн, их интерференция приводит к возникновению областей с минимальным и максимальным значениями амплитуды колебаний
Интерференция и дифракция механических волн.
Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении.
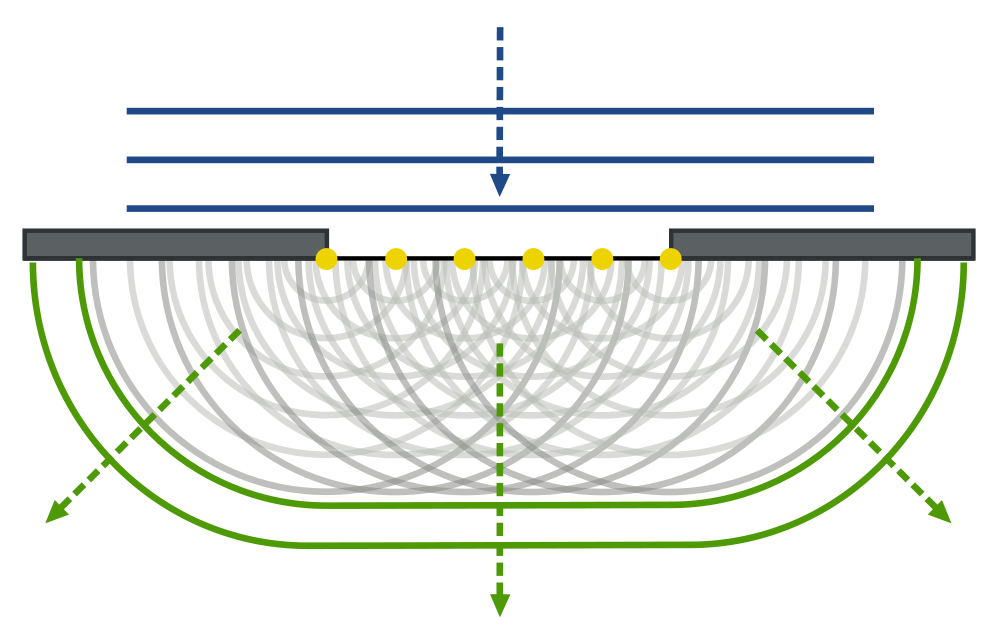
При наложении волн может наблюдаться явление интерференции. Явление интерференции возникает при наложении когерентных волн.
Когерентными называют волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.
Интерференцией называется постоянное во времени явление взаимного усиления и ослабления колебаний в разных точках среды в результате наложения когерентных волн.
Результат суперпозиции волн зависит от того, в каких фазах накладываются друг на друга колебания.
Если волны от источников А и Б придут в точку С в одинаковых фазах, то произойдет усиление колебаний; если же – в противоположных фазах, то наблюдается ослабление колебаний. В результате в пространстве образуется устойчивая картина чередования областей усиленных и ослабленных колебаний.
Условия максимума и минимума
Если колебания точек А и Б совпадают по фазе и имеют равные амплитуды, то очевидно, что результирующее смещение в точке С зависит от разности хода двух волн.
Если разность хода этих волн равна целому числу волн (т. е. четному числу полуволн) Δd = kλ , где k = 0, 1, 2, . то в точке наложения этих волн образуется интерференционный максимум.
Условие максимума:
Амплитуда результирующего колебания А = 2x0.
Если разность хода этих волн равна нечетному числу полуволн, то это означает, что волны от точек А и Б придут в точку С в противофазе и погасят друг друга.
Условие минимума:
Амплитуда результирующего колебания А = 0.
Если Δd не равно целому числу полуволн, то 0
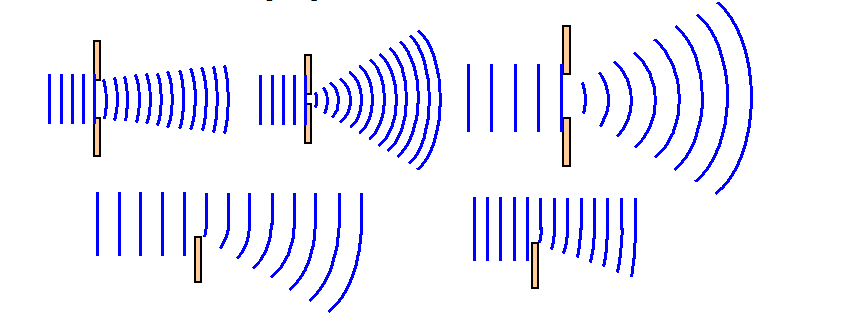
Явление отклонения от прямолинейного распространения и огибание волнами препятствий называется дифракцией.
Соотношение между длиной волны (λ) и размерами препятствия (L) определяет поведение волны. Дифракция наиболее отчетливо проявляется, если длина набегающей волны больше размеров препятствия. Опыты показывают, что дифракция существует всегда, но становится заметной при условии d
Дифракция – общее свойство волн любой природы, которая происходит всегда, но условия её наблюдения разные.
Волна на поверхности воды распространяется в сторону достаточно большого препятствия, за которым образуется тень, т.е. волнового процесса не наблюдается. Такое свойство используется при устройстве волноломов в портах. Если же размеры препятствия сравнимы с длиной волны, то за препятствием будет наблюдаться волнение. Позади него волна распространяется так, как будто препятствия не было вовсе, т.е. наблюдается дифракция волны.
Примеры проявления дифракции. Слышимость громкого разговора за углом дома, звуки в лесу, волны на поверхности воды.
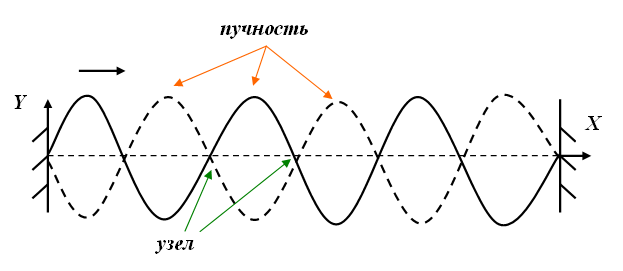
Стоячие волны
Стоячие волны образуются при сложении прямой и отраженной волны, если у них одинаковая частота и амплитуда.
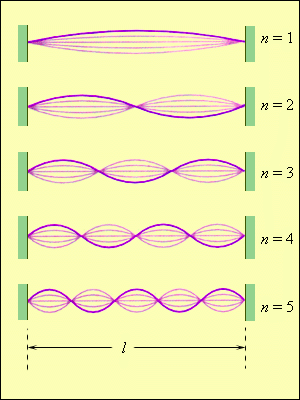
В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.
Колебания струны. В закрепленной с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие волны, причем в местах закрепления струны должны располагаться узлы. Поэтому в струне возбуждаются с заметной интенсивностью только такие колебания, половина длины волны которых укладывается на длине струны целое число раз.
Отсюда вытекает условие
Длинам волн соответствуют частоты
n = 1, 2, 3. Частоты v n называются собственными частотами струны.
Гармонические колебания с частотами v n называются собственными или нормальными колебаниями. Их называют также гармониками. В общем случае колебание струны представляет собой наложение различных гармоник.
Уравнение стоячей волны:
В точках, где координаты удовлетворяют условию 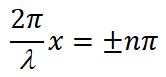
В точках, координаты которых удовлетворяют условию 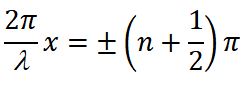
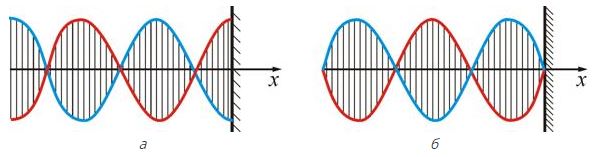
Образование стоячих волн наблюдают при интерференции бегущей и отраженных волн. На границе, где происходит отражение волны, получается пучность, если среда, от которой происходит отражение, менее плотная (a), и узел – если более плотная (б).
Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях.
Стоячие волны возникают, например, в закреплённой с обоих концов натянутой струне при возбуждении в ней поперечных колебаний. Причём в местах закреплений располагаются узлы стоячей волны.
Если стоячая волна устанавливается в воздушном столбе, открытом с одного конца (звуковая волна), то на открытом конце образуется пучность, а на противоположном – узел.
- Цепи с распределенными параметрами
- Уравнения однородной линии
- Решение уравнений однородной линии для установившихся режимов
- Режим синусоидального напряжения
- Бегущие и стоячие волны
- Вторичные параметры однородной линии
- Линия без искажений
- Линия без потерь
- Режимы работы линии без потерь. Стоячие волны
- Входное сопротивление линии
- Линия как элемент резонансной цепи
- Искусственные линии
- Уравнение прямой и обратной волны
- 🎥 Видео
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Цепи с распределенными параметрами
Содержание:
Цепи с распределенными параметрами:
Как было показано в гл. I, электрическое и магнитное поле, а также превращение электромагнитной энергии в тепло, имеют место в каждом элементарном участке любых электрических устройств — индуктивных катушках, обмотках электрических машин и трансформаторов, линиях передачи электрической энергии и т. п. Следовательно, все устройства являются цепями с распределенными индуктивностью, емкостью и сопротивлением.
Однако, когда эти устройства рассматриваются в целом, они обычно заменяются эквивалентными двухполюсниками или четырехполюсниками с сосредоточенными параметрами г, L и С. Если устройство работает при одной частоте, эквивалентные схемы приводятся к простейшим — последовательному или параллельному соединению активного и реактивного сопротивлений для двухполюсника и к Т-образной или П-образной схеме с теми же элементами для четырехполюсника.
Если необходимо провести анализ для некоторого диапазона частот, эквивалентная схема становится тем сложней, чем шире этот диапазон. В общем случае приходится рассматривать цепь такой, какая она есть в действительности, т. е. как цепь с распределенными параметрами.
Необходимость рассмотрения устройств как цепей с распределенными параметрами возникает также в тех случаях, когда анализ должен выявить соотношения внутри устройства, например требуется определить напряжение и ток в разных точках линии передачи.
Далее методы расчета цепей с распределенными параметрами изучаются на примере однородных линий передач, широко применяемых в электроэнергетике и технике электрической связи.
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Уравнения однородной линии
В двухпроводных однородных линиях индуктивность и сопротивление линии, а также емкость и проводимость через несовершенную изоляцию между проводами можно считать распределенными равномерно. Эти параметры на единицу длины двухпроводной линии, подсчитанные для линий различной конфигурации, в дальнейшем обозначены, соответственно, L, г, с, g.
Бесконечно малый элемент двухпроводной линии длиной dx может быть заменен эквивалентной схемой с параметрами Ldx, rdx, Cdx и rdx. На рис. 20.1 эта схема изображена жирными линиями и выбраны управления напряжений и токов. При этом индуктивность и сопротивление являются продольными параметрами линии, а емкость и проводимость — ее поперечными параметрами.
В каждом элементе dx линии происходит падение напряжения
В общем случае переменных напряжений и токов для элемента, расположенного на расстоянии х от конца линии и отмеченного на рис. 20.1 жирными линиями,
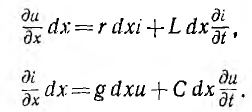
После сокращения на dx получается система уравнений в частных производных для мгновенных значений напряжений и токов:
решение которой при заданных начальных и граничных условиях определит u и i в функции х и t.
При анализе процессов в трехфазной линии каждая ее фаза может рассматриваться, как однофазная двухпроводная линия. Не приводя вывода, можно, например, указать, что для симметричной трехфазной воздушной линии, провода которой расположены в вершинах равностороннего треугольника и удалены от земли, эквивалентная каждой фазе двухпроводная линия имеет индуктивность I, вдвое меньшую, а емкость С, вдвое большую, чем двухпроводная линия с таким же расстоянием между проводами, как и трехфазная линия. Сопротивление г эквивалентной двухпроводной линии равно сопротивлению провода одной фазы, а проводимость g — проводимости одной фазы по отношению к земле.
Решение уравнений однородной линии для установившихся режимов
Режим постоянного напряжения:
Если к началу линии приложено постоянное напряжение U01, npи установившемся режиме напряжения и токи в линии будут также постоянными. При подстановке в уравнения линии вместо переменных мгновенных значений u и i постоянных во времени U0 и I0 в каждой точке линии производные по t будут равны нулю и уравнения станут обыкновенными дифференциальными уравнениями, в которых независимой переменной является x — расстояние от конца линии:
Для получения из приведенной выше системы одного уравнения с одним неизвестным U0 надо взять производную по х от первого уравнения:
и подставить сюда значение 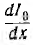
Если положить, что 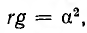
Характеристическое уравнение и его корни имеют вид:
Общее решение для напряжения на расстоянии х от конца линии получает вид:
Следовательно, ток в этой точке
Отсюда видно, что однородную линию характеризуют две величины: 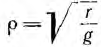
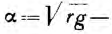
Постоянные интегрирования определяются из граничных условий, которыми могут быть две из четырех величин, например напряжение U01 ток I01 в начале линии или U02, I02 в конце линии. Пусть заданы напряжение U02 и сопротивление r2 нагрузки и тем самым ток 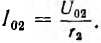
Откуда
Следовательно, напряжение и ток на расстоянии х от конца линии будут:
Таким образом, напряжение и ток в любой точке линии определяются алгебраическими суммами ординат двух экспоненциальных кривых. Ординаты кривой с 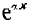
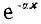
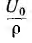
Следовательно, в однородной линии постоянного тока происходит затухание напряжения и тока вдоль линии, определяемое коэффициентом распространения 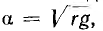
Режим синусоидального напряжения
Если к началу линии приложено синусоидальное напряжение постоянной угловой частоты ω, при установившемся режиме напряжение и ток в каждой точке линии будут также синусоидальными функциями времени той же частоты. Так как синусоидальные напряжение и ток являются частным случаем переменных и и i, в расчетах надо учесть все параметры линии рис. 20.1, т. е. r, L, g и С.
Применяя символический метод, можно использовать результаты расчета для линии постоянного тока (п. 1), заменив продольное сопротивление r комплексным сопротивлением 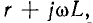
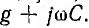
Вещественная часть а коэффициента распространения является коэффициентом затухания, а мнимая 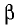
При указанном переходе от постоянного тока к синусоидальному комплексные напряжения и ток на расстоянии х от конца линии получают вид:
Если ввести гиперболические функции
выражения для 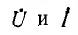
Эти уравнения аналогичны уравнениям для однородных симметричных цепных схем, что и следовало ожидать, так как однородная линия рассматривалась как однородная цепная схема с бесконечно большим числом элементарных звеньев.
Однородная линия в целом является симметричным пассивным четырехполюсником. Его уравнения получают из последних выражений при х =1, где 1 — длина линии:
Параметры этого четырехполюсника
Из уравнений линии видно, что напряжение и ток в любой точке линии являются также функцией частоты ω, так как от нее зависят волновое сопротивление Z, коэффициент распространения у и его составляющие 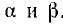
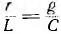
и, следовательно, коэффициент затухания а = 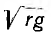
является вещественным числом, т. е. активным сопротивлением, также независящим от частоты. В результате передача будет осуществляться без искажения. Такая линия называемся неискажающей.
Бегущие и стоячие волны
Уравнения линии для режима синусоидального напряжения могут быть преобразованы. После введения значения 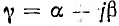
комплекс напряжения в линии получает вид:
Переходя к мгновенному значению напряжения
его можно рассматривать как сумму двух составляющих 
В любой фиксированный момент времени первая составляющая иА распределена вдоль линии по закону синуса с амплитудой, которая и соответствии с множителем е» возрастает от конца линии к ее началу, т. е. затухает от начала линии к ее концу. Если в данный момент времени I’ в точке х’
то в точке х» 2 , прив р, тогда коэффициент отражения n от конца линии равен отношению отраженной волны к падающей, вычисленному в п. 2:
и. волна напряжения U0 отразится от конца линии без перемены знака, а волна тока I0 с переменой знака. На рис. 20.11, а показан напряжение и ток линии после отражения для г2 = 4р, т.е. для = 0,6. Отраженные волны 0,6 U0 и — 0,6 I0 увеличивают напряжение до 1,6 U0 и уменьшают ток до 0,4 I0. После отражения от начала инии волна — 0,6 U0 снизит напряжение линии до U0, а волна — 6 I0 снизит ток до — 0,2 I0 (рис. 20.11, б). В результате второго отра-ения от конца линии напряжение на ней будет 0,64 U0, а ток 0,16 I0 же. 20.11, в) и т. д.
При включении короткозамкнутой линии ее конец, как. и начало, удут отражать волну напряжения с переменой знака, а волну тока — без перемены. При включении такой линии волны напряжения U0 I тока I0 при t 1 Обоснованием высказанного положения является линейность уравнений (11-2) и (11-3), так как только в таких уравнениях сохраняется синусоидальность всех функций.
Применяя комплексную форму записи, перепишем уравнения в комплексном виде: 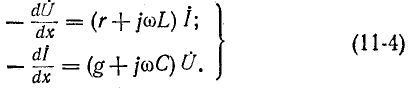
Ввиду того что комплексные значения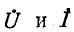
Исключая из системы (11-4) ток 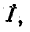
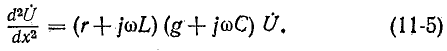
Аналогично, исключая из (11-4) напряжение 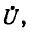
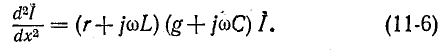
Обозначим квадратный корень из комплексного множителя при 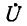
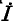
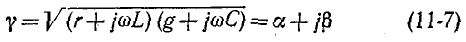
и назовем эту величину коэффициентом распространения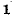
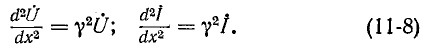
Получились одинаковые однородные линейные дифференциальные уравнения второго порядка. Решение первого из них имеет вид:
Ток 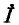
или
где
называется волновым сопротивлением линии
Смысл такого названия объяснен дальше. Подставив (11-7) в (11-9), получим:
Мгновенное значение напряжения в точке х равно мнимой части выражения
здесь 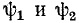
Таким образом, мгновенное значение напряжения в любой точке линии слагается из двух функций.
Рассмотрим вначале первую из этих слагающих функций.
Если считать точку х фиксированной и рассматривать изменение напряжения в данной точке в зависимости от времени, то первая слагающая выражения (11-12) представит собой синусоидальную функцию с постоянной амплитудой.
Если же считать момент времени t фиксированным и рассматривать изменение мгновенного напряжения вдоль линии (т. е. в зависимости от х), то получим затухающую синусоидальную волну напряжения, амплитуда которой 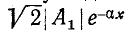
Величина а, характеризующая изменение амплитуды волны на единицу длины линии, называется коэффициентом ослабления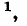
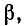
Убывание амплитуды волны вдоль линии обусловливается потерями в линии, а изменение фазы — конечной скоростью распространения электромагнитных колебаний.
Оба эти коэффициента а и 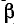
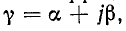
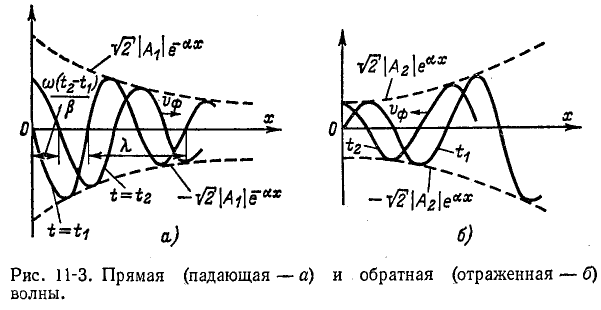
На рис. 11-3, а буквой 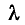
Полученная формула выражает зависимость, существующую между длиной волны и коэффициентом фазы линии.
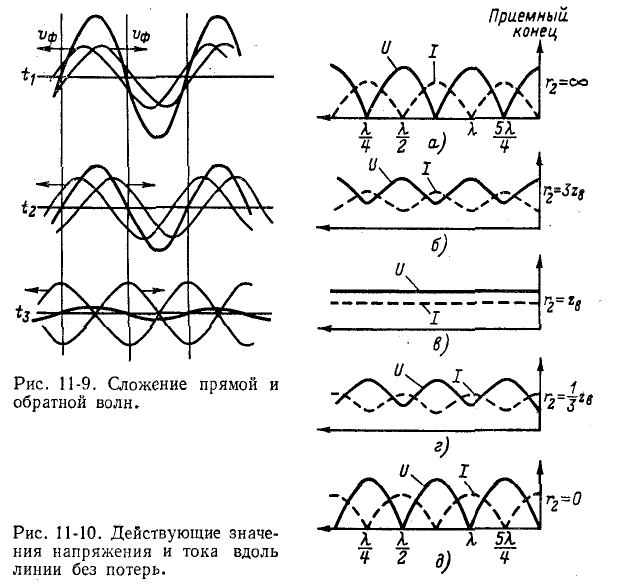
На рис. 11-3, а изображены волны напряжения, соответствующие двум следующим друг за другом моментам времени:
С течением времени волна перемещается от начала линии к ее концу; она носит название прямой, или п а-дающей, волны.
Скорость перемещения падающей волны вдоль линии, называемая фазовой скоростью волны 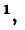
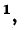
Эго условие записывается для прямой волны в виде
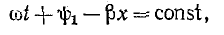
откуда
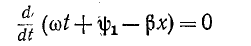
и, следовательно, 
Аналогичное исследование второго слагаемого выражения (11-12) показывает, что для произвольного момента времени оно представляет синусоидальную волну, амплитуда которой 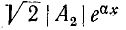
Фазовая скорость обратной волны получается равной
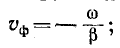
движется в направлении, противоположном направлению прямой волны.
Итак, мгновенное напряжение можно рассматривать как сумму двух волн, движущихся в противоположных направлениях, причем каждая из этих волн затухает в направлении движения.
На основании (11-13) и (11-14) 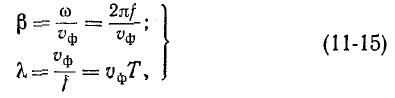
т. е. за время, равное одному периоду, как падающая, так и отраженная волны перемещаются на расстояние, равное длине волны.
Линии, физическая длина которых соизмерима с длиной волны, считаются длинными линиями. При достаточно высоких частотах практически любая протяженная электрическая цепь становится «длинной» по отношению к длине волны.
Как будет показано ниже, фазовая скорость в воздушной линии близка к скорости света
и поэтому частоте 50 Гц будет соответствовать длина волны 6000 км, а частоте 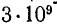
Возвращаясь к уравнениям (11-9) и (11-10) и записывая прямую и обратную волны в комплексной форме, имеем:
Напряжение и ток прямой и соответственно обратной волн связаны законом Ома: 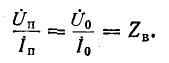
Это соотношение объясняет смысл названия 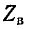
Постоянные интегрирования 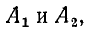
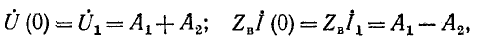
откуда
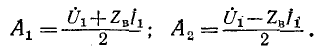
Введем понятие коэффициента отражения волны в начале линии:
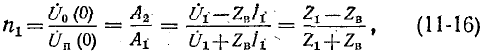
где 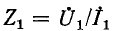
Подстановка выражений для 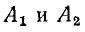
Если заданы граничные условия на конце линии, то удобнее отсчитывать расстояние от конца, приняв координату х’.
Заменяя в уравнениях (11-9) и (11-10) х на (l — х’) и используя заданные граничные условия 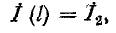
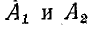
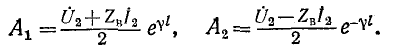
Подставив их в (11-9) и (11-10), получим окончательные выражения для
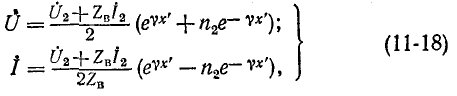
где аналогично предыдущему 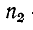
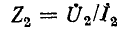
Если сопротивление приемника равно волновому сопротивлению линии 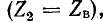
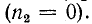
Это важное свойство реализуется в линиях связи, отражения в которых нежелательны по ряду причин.
Во-первых, если затухание в линии невелико, то отраженная волна создает эффект эха в начале линии.
Во-вторых, отражения связаны с потерей энергии. Часть энергии, достигшая приемного конца, не поступает в приемник, а возвращается по линии в виде энергии отраженной волны. При этом возникают дополнительные потери энергии в сопротивлении r и проводимости g линии. Если сопротивление источника, питающего линию, не равно волновому сопротивлению линии, то отраженная волна, достигнув начала линии, претерпевает повторное отражение и т. д. Происходящая вследствие этого потеря энергии в линии понижает общий к. п. д. передачи.
В-третьих, в случае отражений может иметь место нежелательное увеличение напряжения или тока в линии.
Вследствие указанных причин на практике стремятся согласовать сопротивление приемника с волновым сопротивлением линии. При согласовании нагрузки с линией выражения (11-18) упрощаются: с учетом того, что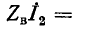
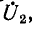
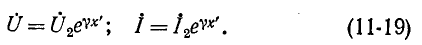
Эти выражения показывают, что при перемещении точки наблюдения вдоль линии, нагруженной согласованно-на конце, в направлении от конца к началу линии, модуль напряжения возрастает в 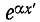
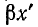
Уравнения (11-19) аналогичны уравнениям симметричного четырехполюсника при согласованной нагрузке. Поэтому показатель распространения на всю длину линии 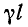
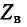
Выражения (11-19) показывают, что при согласованной нагрузке 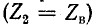
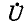
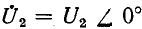
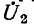
Большой интерес представляет также рассмотрение двух частных случаев нагрузки линии, а именно случаев, когда линия на конце разомкнута (режим холостого хода)
или замкнута (режим короткого замыкания). В первом случае 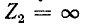

К рассмотрению этих двух случаев мы вернемся несколько позже.
Система уравнений (11-18) может быть переписана в следующем виде:
Уравнения (11-18) и (11-20) представляют собой уравнения линии в показательной (или волновой) форме при отсчете расстояния от конца линии. Они преобразуются с помощью гиперболических функций:
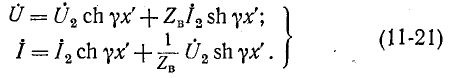
Положив в этих уравнениях х’ = l, получим уравнения линии в гиперболической форме, выражающие напряжение и ток в начале через напряжение и ток в конце линии:
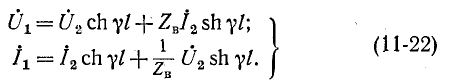
Обращает на себя внимание сходство полученных уравнений с уравнениями симметричного четырехполюсника. Эти уравнения показывают, что однородная линия представляет собой симметричный четырехполюсник с характеристическими параметрами 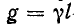
Применяя параметры 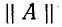
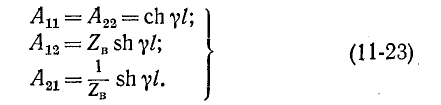
Показательная и гиперболическая формы записи уравнений линии (11-18) и (11-21) дополняют друг друга и применяются в зависимости от условий задачи.
Преимущество показательной формы записи уравнений заключается в большей наглядности рассмотрения физических процессов в линии с помощью прямых и обратных волн и удобстве построения геометрических мест на комплексной плоскости. Поэтому уравнения (11-18) широко использованы в последующих параграфах данной главы.
Гиперболическая форма записи уравнений также представляет в ряде случаев известные удобства с точки зрения исследования и расчета электрических величин в линии и их фазовых соотношений.
Рассмотрение линии как четырехполюсника базируется обычно на гиперболической форме записи уравнений.
Вторичные параметры однородной линии
Вторичными, или характеристическими, параметрами линии являются коэффициент ослабления, коэффициент фазы 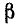
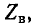
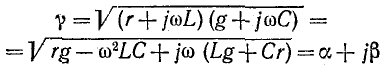
Совместное решение этих уравнений дает:
Из полученных выражений следует, что 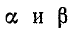
Формула (11-25) позволяет выразить фазовую скорость распространения электромагнитной волны через первичные параметры линии и частоту по формуле (11-14).
Выражения (11-24) и (11-25) неудобны для практического использования ввиду их громоздкости. Существует ряд приближенных расчетных формул для вычисления вторичных параметров линии, учитывающих, что в области высоких частот (порядка 1 МГц и выше) сопротивление r весьма мало по сравнению 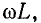
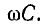
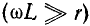
Используя для выражения
бином Ньютона, ограничиваясь первыми двумя членами разложения
и пренебрегая ввиду малости слагаемым — 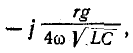
Эти формулы представляют собой пределы, к которым стремятся коэффициент ослабления и коэффициент фазы с ростом частоты.
Выражение (11-28) не следует понимать в том смысле, что а не зависит от частоты; входящие в него параметры r и g сами являются функциями частоты.
Первое слагаемое в правой части выражения (11-28) определяет ту долю ослабления, которая обусловливается продольным активным сопротивлением линии. Второе слагаемое определяет долю ослабления, которая вносится в передачу вследствие наличия поперечной активной проводимости линии.
Для уменьшения потерь при передаче электромагнитной энергии по линии стремятся к тому, чтобы сопротивление линии r и проводимость изоляции g были по возможности малы.
Фазовая скорость согласно (11-14) и (11-29) равна:
Это предельная фазовая скорость распространения волны вдоль линии при бесконечно большой частоте. При постоянном токе 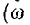
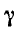
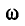
На рис. 11-5 показан характер изменений а и 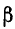
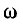
где m — масштабный коэффициент.
Для кабельных линий характерна резко выраженная емкостная проводимость 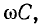
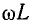
или
Соответственно фазовая скорость распространения волны в кабельной линии равна
т. е. прямо пропорциональна корню квадратному из частоты.
В теории электромагнитного поля доказывается, что произведение удельных значений индуктивности и емкости в линии
где с — скорость света в пустоте (около 3* 108 м/с); 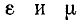
Предел, к которому с ростом частоты стремится фазовая скорость волны, равен на основании (11-30) и (11-33): 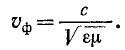
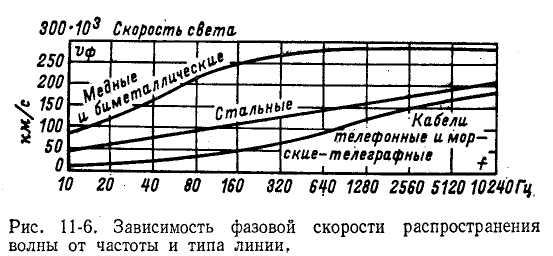
В случае воздушной линии 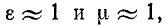
В случае кабельной линии 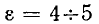
Рисунок 11-6 иллюстрирует зависимость фазовой скорости волны от частоты и типа линии.
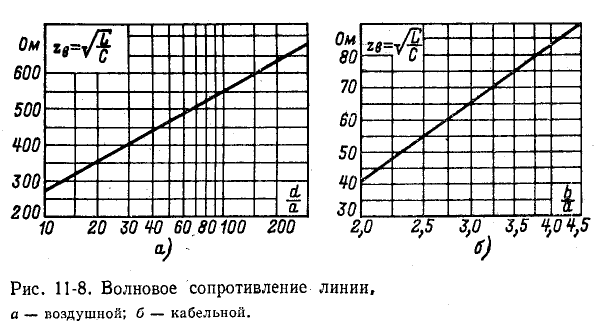
Волновое сопротивление линии
при постоянном токе 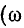
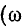
В остальной части диапазона частот волновое сопротивление линии имеет емкостный характер, так как обычно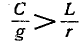
правой части (11-34) больше аргумента числителя].
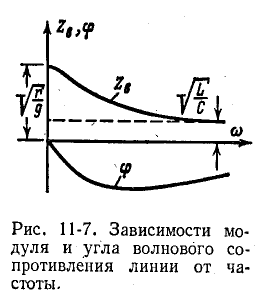
На рис. 11-7 показаны кривые изменения модуля 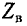
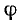
Подставив выражения для L и С в формулу 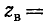
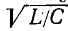
Средние значения 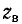
Рисунок 11-8 иллюстрирует графические зависимости 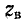
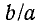
Линия без искажений
Сигналы, передаваемые по линии связи, представляют собой совокупность множества различных частот: дискретных — в случае периодических несинусоидальных сигналов и образующих непрерывный спектр — в случае непериодических сигналов.
Неискаженной передачей сигнала называется такая передача, при которой форма сигнала в начале и конце линии одинакова, т. е. все ординаты кривой напряжения или тока в конце линии прямо пропорциональны соответствующим ординатам кривой в начале линии. Такое явление имеет место в том случае, когда коэффициент ослабления линии, а также фазовая скорость на всех частотах одинаковы.
Неодинаковое затухание на разных частотах создает так называемые амплитудные искажения, а неодинаковая скорость волн на разных частотах — фазовые искажения.
Согласно (П-31) и (11-32) коэффициент ослабления и фазовая скорость в случае кабельных линий пропорциональны квадратному корню из частоты. В случае воздушных линий также существует зависимость а и 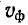
Итак, для неискаженной передачи требуется, чтобы коэффициент ослабления а не зависел от частоты, а коэффициент фазы 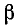
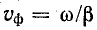
Такое положение имеет место при условии, что
В этом случае коэффициент распространения равен:
Если считать, что первичные параметры линии не зависят от частоты, то коэффициент ослабления в данном случае будет постоянен: 
а коэффициент фазы — прямо пропорционален частоте: 
Линия, параметры которой удовлетворяют условию (11-36), называется линией без искажений, поскольку любые сигналы распространяются по ней с сохранением их формы. Линия без искажений является одновременно и линией с минимальным затуханием, которое только и возможно при заданных параметрах r и g.
Волновое сопротивление линии без искажений — действительное число, что равносильно активному сопротивлению, не зависящему от частоты; в соответствии с (11-34) оно выражается простой формулой 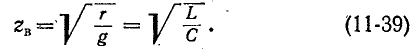
Фазовая скорость в линии без искажений постоянна и совпадает с полученным ранее выражением (11-30) для предельной скорости распространения волны вдоль линии при бесконечно большой частоте: 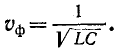
Для устранения искажений, вызываемых несогласованностью сопротивления приемника с сопротивлением линии, т. е. во избежание возникновения отражений на приемном конце, сопротивление приемника должно быть равно 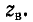
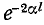
Ввиду того что волновое сопротивление линии без искажений является активным, при согласованной нагрузке напряжение и ток в любой точке линии совпадают по фазе. Отношение мгновенных значений напряжения и тока в любой точке такой линии равно: 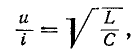
откуда
Следовательно, на любом отрезке линии без искажений, нагруженной согласованно, энергия магнитного поля в каждый момент времени равна энергии электрического поля.
Следует заметить, что на практике условие (11-36), как правило, не выполняется; отношение 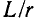
Чтобы линия наиболее соответствовала условию (11-36), следовало бы изменить какой-либо первичный параметр, например уменьшить r или С либо увеличить g или L.
Уменьшение активного сопротивления r возможно за счет применения проводов большего диаметра, что, однако, значительно удорожало бы линию. Увеличение проводимости изоляции g невыгодно, так как при этом возросло бы затухание линии.
Наилучшим средством для приближения первичных электрических параметров к оптимальному соотношению (11-36) является искусственное увеличение индуктивности включением в линию через определенное расстояние индуктивных катушек или применением кабеля, проводящие жилы которого обмотаны тонкой лентой из материала с высокой магнитной проницаемостью.
Линия без потерь
Независимо от того, соблюдается ли оптимальное соотношение первичных параметров (11-36) или не соблюдается, во всех случаях желательно, чтобы активное сопротивление r и проводимость изоляции g были по возможности малы (для уменьшения потерь энергии).
В воздушных линиях обычно индуктивное сопротивление линии 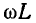
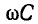
В ряде случаев оказывается полезным в первом приближении рассматривать линию, не имеющую потерь, т. е. пренебрегать активными сопротивлением и проводимостью по сравнению с соответствующими реактивными составляющими. Такая идеализация допускается для приближенной качественной и количественной оценки исследуемых явлений. При этом весьма упрощаются расчетные выражения и гиперболические уравнения линии переходят в тригонометрические.
Итак, основным исходным предложением, которое делают при рассмотрении линии без потерь, .является приближенное условие, что 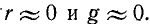
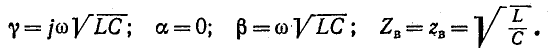
Саедовательно, в линии без потерь ослабление отсутствует. Ввиду постоянства фазовой скорости
отсутствуют также фазовые искажения.
Выражения для коэффициента фазы, фазовой скорости и волнового сопротивления линии без потерь совпадают с выражениями, полученными для линии без искажений. Следовательно, все сказанное о линии без искажений полностью относится и к линии без потерь.
Ввиду того, что гиперболические функции с мнимым аргументом преобразуются в тригонометрические функции, гиперболические уравнения линии (11-21) принимают тригонометрическую форму: 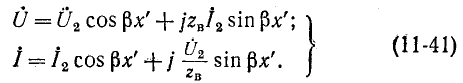
Эти уравнения используются ниже при рассмотрении стоячих волн в линии без потерь.
Энергия, передаваемая по линии, складывается из энергии электрического и магнитного полей.
В том случае, когда к концу линии без потерь присоединено сопротивление, равное волновому, на любом отрезке линии соблюдается условие (11-40), полученное для линии без искажении. При этом вся энергия, доставляемая падающей волной, поглощается в сопротивлении нагрузки.
Если сопротивление нагрузки отлично от волнового, то в месте присоединения нагрузки энергия перераспределяется между полями, в результате чего возникают отражения.
В предельном случае, когда линия на конце разомкнута, падающая волна встречает бесконечно большое сопротивление; ток в конце линии обращается в нуль, и соответственно энергия магнитного поля переходит в энергию электрического поля. Напряжение на разомкнутом конце линии удваивается, и возникает отраженная волна того же знака, что и падающая 
В другом предельном случае, когда линия на конце замкнута накоротко,, падающая волна встречает сопротивление, равное нулю, напряжение в конце линии обращается в нуль и соответственно энергия электрического поля переходит в энергию магнитного поля. Ток на короткозамкнутом конце линии удваивается, и возникает отраженная волна, знак которой противоположен знаку падающей волны 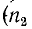
При активной нагрузке 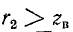
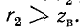
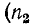
Режимы работы линии без потерь. Стоячие волны
Исследуем закон распределения действующих напряжения и тока вдоль линии без потерь. С этой целью воспользуемся уравнениями линии (11-18) и (11-41) в комплексной и гиперболической формах.
Приняв в (11-18) мнимый коэффициент распространения 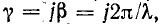
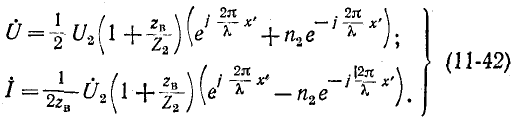
Входящий в эти уравнения коэффициент отражения
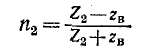
представляет собой в общем случае комплексную величину.
Выражения (11-42) наглядно свидетельствуют о том, что комплексное напряжение в любой точке х’ слагается
из падающей и отраженной волн напряжения, амплитуды которых находятся в соотношении 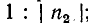
Точкам 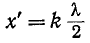
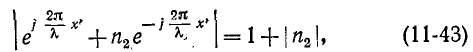
соответствует максимальное действующее значение U, так как при этом фазы падающей и отраженной волн напряжения совпадают. На расстоянии 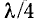
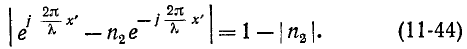
Координаты максимумов и минимумов U, являющиеся многозначными функциями 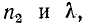
Таким образом, кривая действующих значений напряжения вдоль линии без потерь представляет собой волнообразную кривую, максимумы и минимумы которой чередуются (см. дальше рис. 11-10, б и г).
Аналогичные рассуждения приводят к выводу, что и кривая действующих значений тока вдоль линии без потерь представляет собой волнообразную кривую, смещенную относительно кривой действующих значений напряжения на четверть длины волны. Места максимумов напряжения совпадают с местами минимумов тока и, наоборот, минимумы U совпадают с максимумами I.
При отсутствии отраженной волны 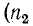
Чем больше приближается коэффициент отражения 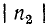
При 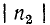
Из сказанного выше следует, что узлы напряжения совпадают с пучностями тока и, наоборот, узлы тока сов-
падают с пучностями напряжения. Соответственно узлы (или пучности) напряжения и тока сдвинуты на четверть длины волны друг относительно друга.
На рис. 11-9 в виде примера показано сложение прямой и обратной волн напряжения, имеющих одинаковые амплитуды, для трех моментов времени: 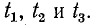
Из этого рисунка видно, что на протяжении всего участка между двумя соседними узлами стоячей волны синусоидальное изменение напряжения во времени происходит с одинаковой начальной фазой: при прохождении узла начальная фаза синусоидальных колебаний изменяется скачкообразно на величину 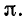
На основании приведенного выше выражения для коэффициента отражения 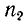
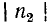
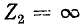
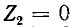
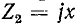
Распределение действующих значений напряжения и тока вдоль линии для холостого хода и короткого замыкания иллюстрируется на рис. 11-10, а и д.
Для сравнения на рис. 11-10 показано распределение напряжения и тока для других режимов работы линии.
При активной нагрузке 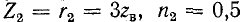
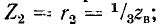
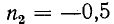
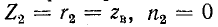
Стоячие волны легко исследуются с помощью уравнений (11-41).линии без потерь.
При холостом ходе 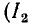
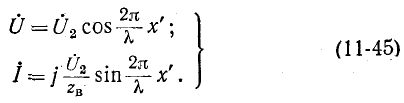
Узлы напряжения находятся в точках, для которых
или 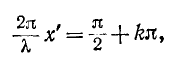
откуда
Пучности напряжения находятся в точках, для которых
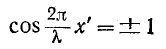
или 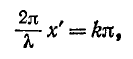
откуда
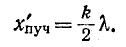
Разомкнутый конец линии совпадает с узлом тока и пучностью напряжения (рис. 11-10, а).
Как видно из (11-45), ток опережает по фазе напряжение на 90°, когда 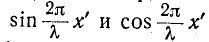
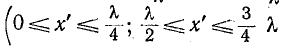
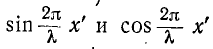
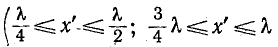
При коротком замыкании, положив в (11-41) 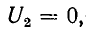
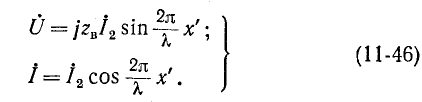
На замкнутом конце линии х’ = 0 и в точках, удаленных от него на целое число полуволн х’ 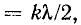
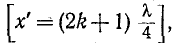
Как видно из (11-46), ток отстает по фазе от напряжения на 90°, когда 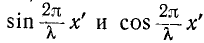
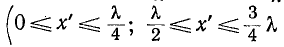
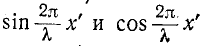
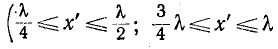
Следует заметить, что наличие хотя бы самых малых потерь в реальных линиях приводит к тому, что действующие значения U и I не снижаются до нуля, а достигают некоторых минимальных значений в точках, соответствующих узлам.
В случае стоячих волн мощность в узлах напряжения и тока равна нулю. В остальных точках линии имеет место только реактивная мощность, так как напряжение и ток сдвинуты по фазе на 90°. В этом случае энергия не передается вдоль линии, а происходит лишь обмен энергией между электрическим и магнитным нолями на участках линии, ограниченных узлами напряжения и тока.
Если в линии имеются потери или приемник потребляет активную мощность, то узлы исчезают; амплитуда падающей волны превышает амплитуду отраженной волны, н за счет разности амплитуд происходит процесс передачи энергии вдоль линии.
Для количественной оценки степени согласования линии с нагрузкой в радиотехнике используется коэффициент бегущей волны, под которым понимается отношение минимума кривой распределения U или I к максимуму той же величины:
С учетом (11-43) и (11-44) имеем:
откуда
В случае активной нагрузки выражение (Н-48) упрощается. При 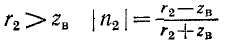
при 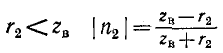
В реальных условиях коэффициент бегущей волны обычно не ниже 0,5—0,6.
Кривую распределения действующих значений напря* жения вдоль линии используют на практике для измерения длины волны или частоты. Длина волны определяется удвоенным расстоянием между соседними максимумами или минимумами кривой распределения, а частота вычисляется по длине волны на основании (11-15).
Входное сопротивление линии
Входное сопротивление линии, измеренное в произвольной точке на _ расстоянии х’ от конца, определяется отношением 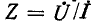
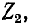
Комплексная форма выражения для входного сопротивления линии получается на основании (11-18): 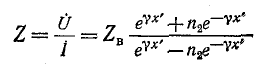
или 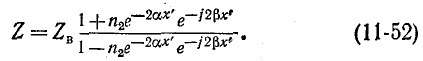
Данное выражение показывает, что с изменением координаты х’ модуль входного сопротивления линии колеблется между некоторыми максимумами и минимумами (которые в общем случае отличаются друг от друга).
Допустим, что модуль Z достигает некоторого максимума в точке 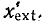
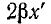
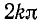
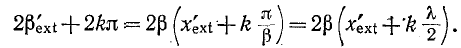
Следовательно, максимумы чередуются через каждые полволны. Посредине между максимумами будут минимумы, которые также чередуются через каждые полволны.
Если вместо координаты 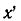

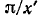
В этом случае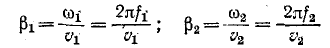
и, следовательно,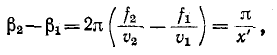
откуда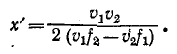
При малом расхождении частот 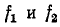
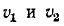
Данная формула позволяет определить расстояние от точки наблюдения до ближайшей точки линии, в которой имеет место отражение (например, при коротком замыкании на линии), производя измерение только в одной точке.
Волнообразный характер кривой z подчиняется в общем случае закону изменения модуля гиперболического тангенса с комплексным аргументом, что видно из следующего вывода.
Непосредственно из (11-21) следует:
Обозначив 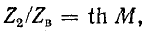
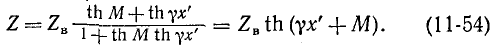
При холостом ходе 

а при коротком замыкании
С учетом (11-55) и (11-56) входное сопротивление Z легко выразить через
Этой формулой пользуются в том случае, когда из опытов холостого хода и короткого замыкания известны
Данные опытов холостого хода и короткого замыкания используются также для вычисления характеристических параметров линии.
На основании (11-55) и (11-56)
Эти формулы совпадают с (9-35). Ввиду того что коэффициент фазы р определяется по (11-57) неоднозначно, при вычислении производится проверка на основании (11-14), причем первоначально фазовая скорость 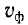
Вычисление характеристических параметров по формулам (11-57) иллюстрировано ниже примером 11-1.
На рис. 11-11 показаны кривые изменения модулей 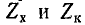
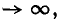
Входные сопротивления линии без потерь при холостом ходе и коротком замыкании могут быть получены из (11-55) и (11-56) заменой
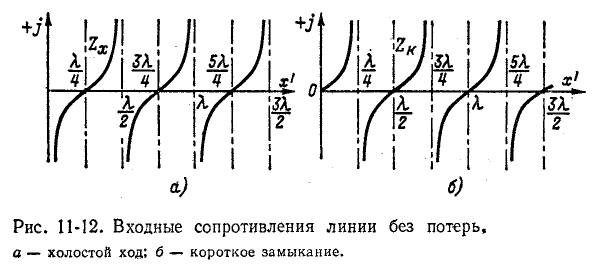
Эти реактивные входные сопротивления с учетом их знака изображаются котангенсоидами и тангенсоидами (рис. 11-12). Аргументом может служить также величина 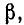
Сопоставляя эти графики с частотными характеристиками сопротивлений реактивных двухполюсников, легко убедиться в их сходстве: резонансы напряжений и токов чередуются, однако в отличие от двухполюсников, имеющих ограниченное число резонансов, линия без потерь имеет бесконечное число резонансных точек, что соответствует представлению линии как цепочки из бесконечного числа индуктивностей и емкостей.
Входное сопротивление линии без потерь при 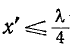
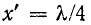
Следует отметить, что в реальных условиях вследствие наличия потерь входное сопротивление линии никогда не снижается до нуля и никогда не достигает бесконечного значения.
При этом короткозамкнутая линия при 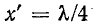
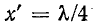
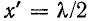
Пример 11-1.
Даны результаты измерения входных сопротивлений линии длиной 160 км на частоте 1000 Гц при холостом ходе и коротком замыкании: 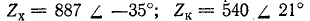
Расчет начинается с вычисления волнового сопротивления и коэффициента распространения:
Целое число к находится на основании ориентировочного расчета величины 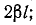
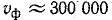
Следовательно, надо принять
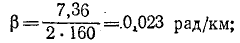
коэффициент распространения
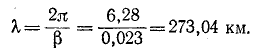
Первичные параметры линии находятся на основании выражений:
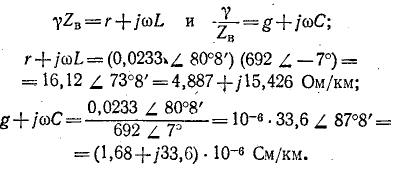
Таким образом,
Линия как элемент резонансной цепи
Четвертьволновая линия с малыми потерями, разомкнутая на конце, обладает свойствами резонансной цепи, состоящей из последовательно соединенных r, L и С. При частоте, при которой на линии укладывается четверть волны (такую частоту условимся называть резонансной), входное сопротивление линии будет активным и притом минимальным.
При малом отклонении частоты от резонансной модуль входного сопротивления линии резко возрастает: входное сопротивление приобретает емкостный характер при понижении частоты и индуктивный характер — при повышении.
Входное сопротивление линии с малыми потерями, разомкнутой на конце, можно получить из (11-21), разлагая 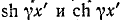
Выражение примет вид: 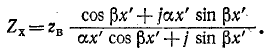
Вблизи резонансной частоты 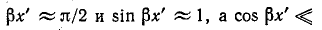
Если через 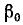
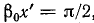
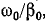
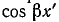
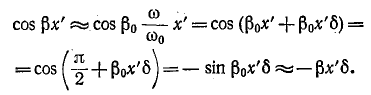
Здесь, так же как и 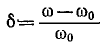
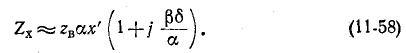
Было показано, что при частоте, близкой к резонансной, когда 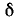

Рассматривая четвертьволновую линию как резонансную цепь, можно в силу одинаковой структуры выражений (11-58) и (11-59) считать, что добротность линии равна:
При этом резонансные характеристики, приведенные, применимы и к рассматриваемой линии.
Соответственно полоса пропускания, представляющая собой величину, обратную добротности, равна: 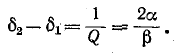
Здесь под полосой пропускания, подразумевается отнесенная к резонансной частоте ширина резонансной кривой между точками, соответствующими половине максимальной мощности (когда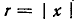
При малых значениях коэффициента а добротность получается высокой, достигая примерно 1000—4000, что намного превышает добротность контуров r, L и С, В связи с этим возрастает и острота настройки.
Искусственные линии
Искусственной линией называется цепь с сосредоточенными параметрами, приближающаяся по своим частотным характеристикам (в заданном диапазоне частот) к цепи с распределенными параметрами.
Искусственные линии находят широкое применение в лабораторных условиях и в особенности в современной импульсной радиотехнике для получения требуемого запаздывания сигналов.
Отмечалось, что всякая однородная линия представляет собой симметричный четырехполюсник с. мерой передачи, равной
и характеристическим сопротивлением, равным волновому:
Заменяя линию эквивалентным Т-образным четырехполюсником, согласно рис. 9-17, а получаем на основании формул (11-23) расчетные выражения:
Для какой-либо фиксированной частоты такой Т-образный четырехполюсник может быть осуществлен. Однако при передаче сигналов в некоторой заданной полосе частот величины 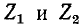
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Электрическая энергия, ее свойства и применение
- Электрическая цепь
- Электрический ток
- Электрические цепи постоянного тока
- Анализ переходных и установившихся процессов методом интеграла свертки
- Операторный метод расчета переходных процессов
- Метод пространства состояний электрических цепей
- Синтез электрических цепей
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Уравнение прямой и обратной волны
Физика
Как происходит распространение колебаний? Необходима среда для передачи колебаний или они могут передаваться без нее? Как звук от звучащего камертона доходит до слушателя? Каким образом быстропеременный ток в антенне радиопередатчика вызывает появление тока в антенне приемника? Как свет от далеких звезд достигает нашего глаза? Для рассмотрения подобного рода явлений необходимо ввести новое физическое понятие – волна . Волновые процессы представляют общий класс явлений, несмотря на их разную природу.
Процесс распространения колебаний в пространстве называется волной .
Волны, образованные внешним воздействием, приложенным к упругой среде, называются бегущими волнами : они “бегут” от создающего их источника. Важное свойство бегущих волн заключается в том, что они переносят энергию и импульс. Если внешняя сила совершает гармонические колебания, то вызванные ею волны называются гармоническими бегущими волнами .
Волновой процесс обусловлен наличием связей между отдельными частями системы, в зависимости от которых, мы имеем упругую волну той или иной природы.
Глава 1. Упругие волны.
1. Упругими или механическими волнами называются механические возмущения (деформации), распространяющиеся в упругой среде.
Деформации в теле или среде называются упругими, если они полностью исчезают после прекращения внешних воздействий.
Тела, которые воздействуют на среду, вызывая колебания, называются источниками волн . Распространение упругих волн не связано с переносом вещества , но волны переносят энергию, которой обеспечивает волновой процесс источник колебаний.
2. Среда называется однородной , если ее физические свойства, рассматриваемые в данной задаче, не изменяются от точки к точке.
Среда называется изотропной , если ее физические свойства, рассматриваемые в задаче, одинаковы по всем направлениям.
Среда называется линейной, если между величинами, характеризующими внешнее воздействие на среду, которое и вызывает ее изменение, существует прямо пропорциональная связь. Например, выполнение закона Гука означает, что среда линейна по своим механическим свойствам.
§ 1.1. Упругие продольные и поперечные волны.
1. Все волны делятся на продольные и поперечные.
Поперечные волны – упругие волны, при распространении которых частицы среды совершают колебания в направлении, перпендикулярном направлению распространения волны.
Продольные волны – упругие волны, при распространении которых частицы среды совершают колебания вдоль направления распространения волны.
Поперечные упругие волны возникают только в твердых телах, в которых возможны упругие деформации сдвига . Продольные волны могут распространяться в жидкостях или газах, где возможны объемные деформации среды , или в твердых телах, где возникают деформации удлинения или сжатия . Исключение составляют поперечные поверхностные волны. Простые продольные колебания – это процесс распространения в пространстве областей сжатий и растяжений среды. Сжатия и растяжения среды образуются при колебаниях ее точек (частиц) около своих положений равновесия.
§ 1.2. Характеристики бегущих волн.
Минимальное расстояние , на которое распространяется волна за время, равное периоду колебания точки среды около положения равновесия, называется длиной волны .
Длиной волны называется наименьшее расстояние между двумя точками среды, совершающими колебания в фазе (т.е. разность их фаз равна ) .
Если точки разделены расстоянием , их колебания происходят в противофазе.
2. Фазовая скорость волны.
Из повседневного опыта известно, что бегущие по воде волны распространяются с постоянной скоростью, пока свойства среды, например, глубина воды, не меняется, что говорит о том, что скорость распространения волнового процесса в пространстве остается постоянной. В случае гармонических бегущих волн (см. определение выше) эта скорость называется фазовой .
Фазовая скорость — это скорость распространения данной фазы колебаний, т.е. скорость волны.
Связь длины волны , фазовой скорости и периода колебаний Т задается соотношением:
Учитывая, что , где — линейная частота волны , — период, а циклическая частота волны , получим разные формулы для фазовой скорости:
Для волнового процесса характерна периодичность по времени и по пространству.
Т – период колебаний точек среды. Роль пространственного периода играет длина волны . Соотношение между периодом и циклической частотой задается формулой: . Аналогичное соотношение можно записать для длины волны и величиной k, называемой волновым числом : .
Таким образом. Можно добавить еще одно уравнение для фазовой скорости:
3. Фазовая скорость различна для разных сред. В случае упругих поперечных волн (в твердом теле) фазовая скорость равна:
где — модуль сдвига среды, -ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).
Фазовая скорость упругих продольных волн в твердом теле равна
где Е — модуль Юнга, — плотность невозмущенной среды (твердого тела до момента распространения по нему волны).
Фазовая скорость продольных волн в жидкости и газе определяется соотношением:
где К – модуль объемной упругости среды – величина, характеризующая способность среды сопротивляться изменению ее объема, — плотность невозмущенной среды.
Фазовая скорость продольных волн в идеальном газе задается формулой:
— показатель адиабаты, — молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа ( ) и от его термодинамического состояния (Т).
4. Фронт волны. Волновая поверхность.
При прохождении волны по среде ее точки вовлекаются в колебательный процесс последовательно друг за другом.
Геометрическое место точек, до которого к некоторому моменту времени дошел колебательный процесс, называется волновым фронтом .
Геометрическое место точек, колеблющихся в фазе, называется волновой поверхностью .
Волновой фронт – частный случай волновой поверхности. Волновой фронт все время перемещается. Волновые поверхности остаются неподвижными. Они проходят через положения равновесия частиц среды, которые колеблются в одинаковой фазе.
При описании распространения волн широко используют понятие луча. Направления, в которых распространяются колебания, называются лучами . В изотропной среде (см. определение выше) лучи перпендикулярны волновым поверхностям (фронту) и имеют вид прямых линий. В анизотропной среде, а также при дифракции волн, лучи могут искривляться.
Форма волнового фронта определяет вид волны: сферические (от точечного источника в изотропной среде), эллиптические (в анизотропной среде), цилиндрические (от протяженных источников), плоские и другие. На достаточно большом расстоянии от источника небольшой участок любого фронта можно считать плоским .
Если известно положение фронта волны в некоторый момент времени и скорость волны , то его положение в последующий момент времени можно определить на основе принципа Гюйгенса . Согласно этому принципу все точки поверхности волнового фронта являются источниками вторичных волн . Искомое положение волнового фронта совпадает с поверхностью, огибающей фронты вторичных волн.
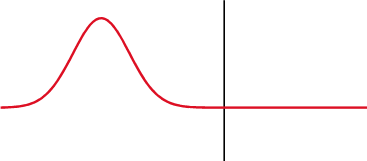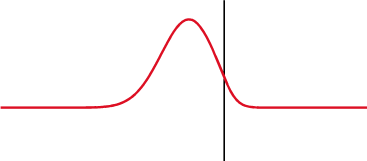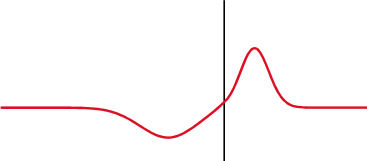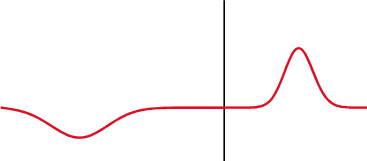
5. Уравнение бегущей волны.
Уравнением упругой волны называется зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при прохождении по ней волны.
Так, для волн в твердом теле такой величиной является смещение от положения равновесия любой точки тела в произвольный момент времени. Для характеристики продольных волн в жидкости или газе используют понятие избыточного давления . Избыточное давление равно разности между давлением в данный момент времени, когда по среде проходит волна, и равновесным, когда возмущений в среде нет.
Получим уравнение бегущей волны в одномерном пространстве, которое предполагаем изотропным и однородным (см. определения выше). Кроме того, силы сопротивления в среде считаем пренебрежимо малыми (т.е. нет затухания колебаний). Пусть точка О — центр (источник) колебаний, она колеблется по закону:
где — смещение точки О от положения равновесия, — частота, А – амплитуда колебаний. Часы или секундомер №1 включаются сразу, как только начинаются колебаний точки О, и отсчитывают время t (Рисунок 2.1.1). Ось ОУ совпадает с направлением распространения волны.
Через промежуток времени процесс колебаний дойдет до точки В, и она будет колебаться по закону:
Амплитуда колебаний в случае отсутствия затухания процесса будет такой же как и амплитуда точки О. Часы или секундомер №2 включаются тогда, когда колебательный процесс дойдет до точки В (т.е. когда начинает колебаться точка В), и отсчитывают время . Моменты времени t и связаны между собой соотношением или . Расстояние между точками О и В обозначим . Фазовая скорость волны равна , тогда . Учитывая соотношения для и и формулы и , можно записать уравнение колебаний точки В в разных видах:
Аналогично уравнению колебаний точки В запишем уравнение колебаний любой точки среды, расположенной на расстоянии y от источника колебаний:
где — волновое число (см. определение выше).
Это уравнение и есть уравнение для смещения любой точки пространства в любой момент времени, т.е. уравнение бегущей волны, где А – амплитуда, величина — фаза волны, которая в отличии от фазы колебаний зависит и от времени “t”, и от расстояния “y” колеблющейся точки от источника колебаний.
Вернемся к разделению волн по форме фронта волны и к понятию луча, как направления распространения колебательного процесса. Учтем, что в изотропной среде лучи перпендикулярны фронту и имеют вид прямых линий. Тогда уравнение бегущей волны, полученное выше, есть уравнение плоской бегущей волны , т.е. когда фронт волны – плоскость.
Уравнение плоской отраженной волны в одномерном пространстве легко получить, если представить ее как бегущую волну в отрицательном направлении оси ОУ, что приведет к замене в уравнении бегущей волны координаты “y” на “-y”:
Упругая волна называется синусоидальной или гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Так, рассмотренные выше бегущая и отраженная волны являются гармоническими волнами.
6. Волновое уравнение.
Когда мы рассматривали колебания, то для любой колебательной системы получали дифференциальное уравнение, для которого соответствующее уравнение колебаний являлось решением. Аналогично уравнение бегущей и отраженной волны являются решениями дифференциального уравнения второго порядка в частных производных, называемого волновым уравнением и имеющего вид:
где — фазовая скорость волны.
Уравнения бегущей и отраженной волн и волновое уравнение представлены для случая одного измерения, т.е. распространения волны вдоль оси ОУ. В волновое уравнение входят вторые частные производные по времени и координате от смещения потому, что есть функция двух переменных t и y.
7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды.
Если смещение любой точки среды с координатой y в момент времени t задано уравнением:
то скорость этой точки есть величина , а ускорение — :
§ 1.3. Энергия упругих волн.
В среде распространяется плоская упругая волна и переносит энергию, величина которой в объеме равна:
где — объемная плотность среды.
Если выбранный объем записать как , где S – площадь его поперечного сечения, а — его длина, то среднее количество энергии, переносимое волной за единицу времени через поперечное сечение S, называется потоком через его поверхность:
Количество энергии, переносимое волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно направлению распространения волны, называется плотностью потока энергии волны.
Эта величина определяется соотношением:
где -объемная плотность энергии волны, — фазовая скорость волны. Так как фазовая скорость волны — вектор, направление которого совпадает с направлением распространения волны, то можно величине плотности потока энергии I придать смысл векторной величины:
Величина , вектор плотности энергии волны , впервые была введена Н.А. Умовым в 1984 году и получила название вектора Умова. Подобная величина для электромагнитных волн называется вектором Умова — Пойнтинга.
Интенсивностью волны называется модуль среднего значения вектора Умова .
§ 1.4. Принцип суперпозиции волн. Групповая скорость.
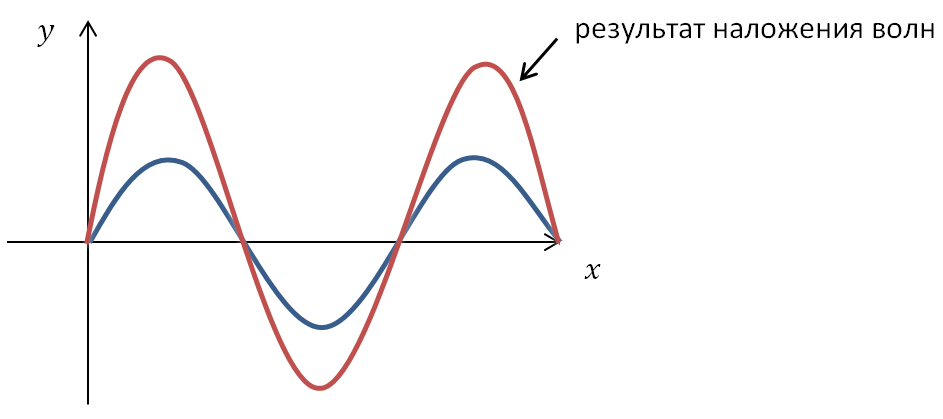
Принцип суперпозиции (наложения) волн установлен на опыте. Он состоит в том, что в линейной среде волны от разных источников распространяются независимо, и накладываясь, не изменяют друг друга. Результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений , которые частица получит, участвуя в каждом из слагаемых волновых процессов.
Согласно принципу суперпозиции накладываться друг на друга без взаимного искажения могут волны любой формы. В результате наложения волн результирующее колебание каждой частицы среды может происходить по любому сложному закону. Такое образование волн называется волновым пакетом. Скорость движения волнового пакета не совпадает со скоростью ни с одной из слагаемых волн. В этом случае говорят о скорости волнового пакета. Скорость перемещения максимума группы волн (волнового пакета) называется групповой скоростью. Она равна скорости переноса энергии волнового пакета.
На практике мы всегда имеем дело с группой волн, так как синусоидальных волн, бесконечных в пространстве и во времени, не существует. Любая ограниченная во времени и пространстве синусоидальная волна есть волновой пакет (его называют цуг волны). Групповая скорость такого пакета совпадает с фазовой скоростью бесконечных синусоидальных волн, результатом сложения которых он является.
В общем виде связь между групповой и фазовой скоростями имеет вид:
§ 1.5. Интерференция волн. Стоячие волны.
1 . Интерференцией волн называется явление наложение двух и более волн, при котором в зависимости от соотношения между фазами этих волн происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других.
В пространстве всегда найдутся такие точки, в которых разность фаз складываемых колебаний равна величине , где k – целое число, т.е. волны (от разных источников) приходят в такие точки в фазе . В них будет наблюдаться устойчивое, неизменно продолжающееся все время усиление колебаний частиц. Найдутся в пространстве, где распространяется несколько волн, и такие точки, где разность фаз будет равна , т.е. волны приходят в эти точки в противофазе . В таких точках пространства будет наблюдаться устойчивое ослабление колебаний частиц.
Устойчивая интерференционная картина возникает только при наложении таких волн, которые имеют одинаковую частоту, постоянную во времени разность фаз в каждой точке пространства. Волны, удовлетворяющие этим условиям и источники, создающие такие волны, называются когерентными. Плоские синусоидальные волны, частоты которых одинаковы, когерентны всегда.
2. Запишем условия максимумов и минимумов при интерференции. Когерентные точечные источники и испускают волны по всем направлениям. До точки наблюдения М расстояние от первого источника , а от второго — .
Колебания точки М под действием волн от двух источников и описываются уравнениями:
Амплитуда результирующего колебания в точке М определится следующим образом (см. раздел “Сложение колебаний”):
Амплитуда колебаний точки М максимальна ( ), если
Величина называется разностью хода двух волн.
Условие максимума при интерференции имеет вид:
Если целое число волн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный максимум.
Амплитуда колебаний точки М минимальна ( ), если
Условие минимума при интерференции имеет вид:
Если нечетное число полуволн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный минимум.
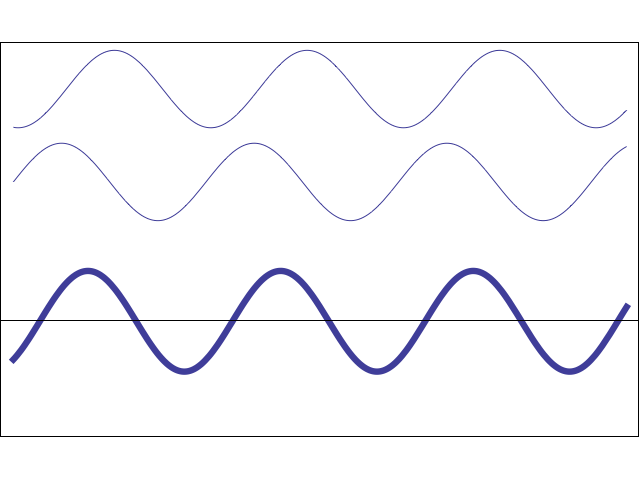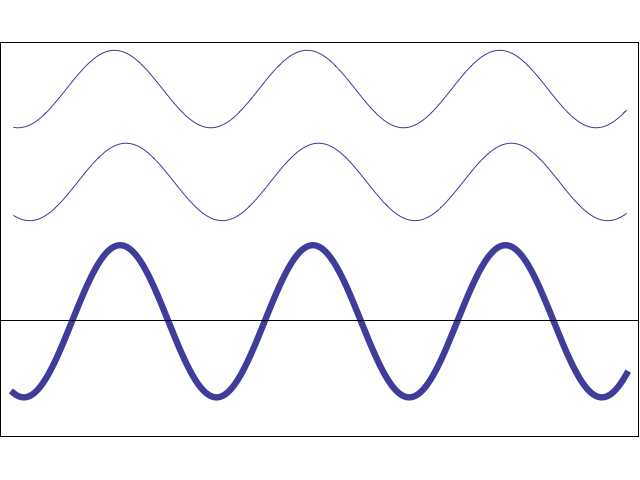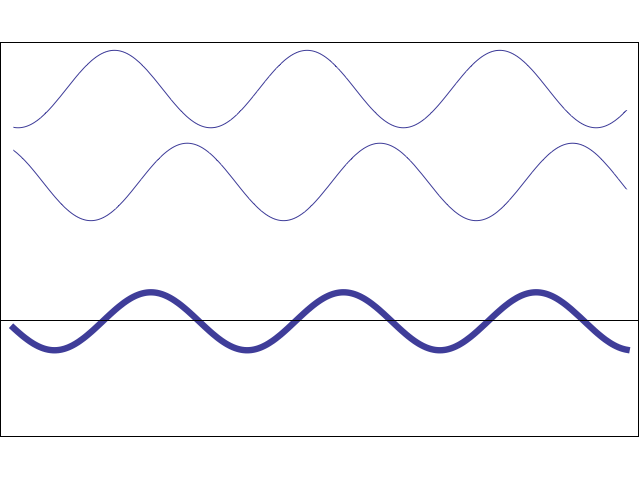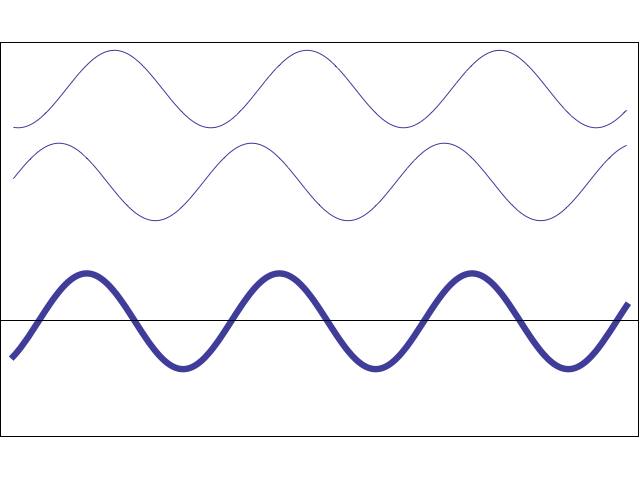
3. Простейший случай интерференции наблюдается при наложении бегущей и отраженной волн, что приводит к образованию стоячей волны. Уравнения бегущей и отраженной волны имеют вид:
Суммарное смещение частицы среды, находящейся на расстоянии y от источника колебаний, равно сумме смещений и :
Это и есть уравнение стоячей волны. Величина — амплитуда, а ( ) — фаза стоячей волны. Можно сказать, что частицы в стоячей волне имеют одну фазу колебаний. Амплитуда колебаний частиц в стоячей волне зависит от их координат (расстояний до источника колебаний), но не зависит от времени. Знак модуля поставлен в формуле для амплитуды стоячей волны, потому что амплитуда – величина положительная.
В стоячей волне есть точки, которые все время остаются неподвижными. Такие точки называются узлами смещения , их положение определяется из условия:
, отсюда следует . Выполнение этого соотношения будет при условии для Итак, координаты узлов задаются формулой:
Расстояние между двумя соседними узлами равно .
Точки среды, колеблющиеся с наибольшей амплитудой, называются пучностями стоячей волны , их положение (координаты) определяются соотношением:
Это уравнение можно получить из условия максимума амплитуды
, т.е. . Последнее соотношение выполняется при значениях аргумента ( ).
Расстояние между двумя соседними пучностями равно .
4. Изменение фазы волны при ее отражении.
Как отмечалось ранее, стоячая волна образуется при сложении бегущей и отраженной волн. Отраженную волну можно рассматривать как бегущую волну, распространяющуюся в обратном направлении и ее можно получить при отражении бегущей волны от границы двух сред. Для синусоидальных волн это означает, что при отражении от более плотной среды фаза волны скачком изменяется на радиан , а при отражении от менее плотной среды фаза волны не изменяется . Изменение фазы на радиан соответствует появлению дополнительного хода луча, равного .
Глава 2. Звуковые волны.
1.Важным видом продольных волн являются звуковые волны . Так называются волны с частотами 17 – 20000 Гц. Учение о звуке называется акустикой. В акустике изучаются волны, которые распространяются не только в воздухе, но и в любой другой среде. Упругие волны с частотой ниже 17 Гц называются инфразвуком, а с частотой выше 20000 Гц – ультразвуком.
Звуковые волны – упругие колебания, распространяющиеся в виде волнового процесса в газах, жидкостях, твердых телах.
2. Избыточное звуковое давление. Уравнение звуковой волны.
Уравнение упругой волны позволяет вычислить смещение любой точки пространства, по которому проходит волна, в любой момент времени. Но как говорить о смещении частиц воздуха или жидкости от положения равновесия? Звук, распространяясь в жидкости или газе, создает области сжатия и разряжение среды, в которых давление соответственно повышается или понижается по сравнению с давлением невозмущенной среды.
Если — давление и плотность невозмущенной среды (среды, по которой не проходит волна), а — давление и плотность среды при распространении в ней волнового процесса, то величина называется избыточным давлением. Величина есть максимальное значение избыточное давление ( амплитуда избыточного давления ).
Изменение избыточного давления для плоской звуковой волны (т.е. уравнение плоской звуковой волны) имеет вид:
где y – расстояние от источника колебаний точки, избыточное давление в которой мы определяем в момент времени t.
Если ввести величину избыточной плотности и ее амплитуды так же, как мы вводили величину избыточного звукового давления, то уравнение плоской звуковой волны можно было бы записать так:
3. Объективные и субъективные характеристики звука.
Само слово “звук” отражает два различных, но взаимосвязанных понятия: 1)звук как физическое явление; 2)звук – то восприятие, которое испытывает слуховой аппарат (человеческое ухо) и ощущения, возникающие у него при этом. Соответственно характеристики звука делятся на объективные , которые могут быть измерены физической аппаратурой, и с убъективные , определяемые восприятием данного звука человеком.
К объективным (физическим) характеристикам звука относятся характеристики, которые описывают любой волновой процесс: частота, интенсивность и спектральный состав. В таблицу 3 включены сравнительные данные объективных и субъективных характеристик.
Характеристики
Объективные характеристики
Высота звука
Высота звука определяется частотой
волны
Тембр (окраска звука)
Тембр звука определяется его спектром
Громкость (сила звука)
Сила звука определяется нтенсивностью волны (или квадратом ее амплитуды)
Остановимся на некоторых определениях.
Частота звука измеряется числом колебаний частиц среды, участвующих в волновом процессе, в 1 секунду.
Интенсивность волны измеряется энергией, переносимой волной в единицу времени через единичную площадь (расположенную перпендикулярно направлению распространению волны).
Спектральный состав (спектр) звука указывает из каких колебаний состоит данный звук и как распределены амплитуды между отдельными его составляющими.
Различают сплошные и линейчатые спектры. Для субъективной оценки громкости используются величины, называемые уровнем силы звука и уровнем громкости. Все акустические величины и их размерности в СИ приведены в приложении.
Глава 3. Электромагнитные волны.
1 . Электромагнитными волнами называются возмущения электромагнитного поля (т.е. переменное электромагнитное поле), распространяющиеся в пространстве.
Утверждение о существовании электромагнитных волн является непосредственным следствием решения системы уравнений Максвелла. Согласно этой теории следует, что переменное электромагнитное поле распространяется в пространстве в виде волн, фазовая скорость которых равна:
где — скорость света в вакууме, , — электрическая и магнитная постоянные, , — соответственно диэлектрическая и магнитная проницаемость среды.
2. Электромагнитные волны — поперечные волны . Векторы Е и Н поля электромагнитной волны взаимно перпендикулярны друг другу. Вектор скорости волны и векторы Е и Н образуют правую тройку векторов (Рисунок 2.1.4).
Для сравнения ориентации тройки векторов , Е и Н на рисунке приведено расположение осей декартовой системы координат. Такое сопоставление уместно и в дальнейшем будет использовано для определения проекций векторов Е и Н на координатные оси.
Взаимно перпендикулярные векторы Е и Н колеблются в одной фазе (их колебания синфазные ). Модули этих векторов связаны соотношением:
которое справедливо для любой бегущей электромагнитной волны независимо от формы ее волновых поверхностей.
3.По форме волновых поверхностей волны могут быть плоские, эллиптические, сферические и т.д..
Монохроматической волной называется электромагнитная волна одной определенной частоты. Монохроматическая волна не ограничена в пространстве и во времени. В каждой точке электромагнитного поля монохроматической волны проекции векторов Е и Н на оси координат совершают гармонические колебания одинаковой частоты . Например, для плоской монохроматической волны, распространяющейся вдоль положительного направления оси ОУ, как показано на рисунке 2.1.3.,ее уравнение имеет вид:
Такие волны называются плоско (или линейно ) поляризованными волнами.
Плоскость, в которой происходит колебание вектора Е называют плоскостью поляризации линейно поляризованной волны, а плоскость колебаний вектора Н – плоскостью колебаний . Ранее эти названия были обратными (см. [1]).
6. Все сказанное о стоячих волнах в упругих средах относится и к электромагнитным волнам. В этом случае, однако, волна характеризуется не одним вектором, а двумя взаимно перпендикулярными векторами Е и Н .
Стоячая электромагнитная волна состоит из двух стоячих волн — магнитной и электрической, колебания которых сдвинуты по фазе на .
7. Энергия электромагнитных волн.
Объемная плотность энергии электромагнитного поля в линейной изотропной среде задается соотношением:
с — скорость света в вакууме.
В случае плоской линейно поляризованной монохроматической волны, распространяющейся вдоль положительного направления ОY, напряженность электрического поля задается уравнением:
соответственно объемная плотность энергии этой волны
Значение объемной плотности энергии волны меняется за период от 0 до .Среднее за период значение энергии равно:
8. Вектор плотности потока энергии электромагнитной волны называется вектором Умова — Пойнтинга:
Для линейно поляризованной монохроматической волны вектор Пойнтинга направлен в сторону распространения волны и численно равен:
Интенсивность электромагнитной волны равна модулю среднего значения вектора Пойнтинга за период его полного колебания:
Интенсивностью электромагнитной волны называется физическая величина, численно равная энергии, переносимая волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны.
Интенсивность бегущей монохроматической волны: — фазовая скорость волны, среднее значение объемной плотности энергии поля волны.
Интенсивность света (электромагнитных волн, рассматриваемых в оптике ) прямо пропорциональна квадрату амплитуды колебаний вектора напряженности Е поля световой волны.
🎥 Видео
Билет №34 "Электромагнитные волны"Скачать

Математика это не ИсламСкачать

Видеоурок "Общее уравнение прямой"Скачать

Лекция 2 ВолныСкачать

Получение уравнения плоской бегущей волны.Скачать

15. Взаимное расположение прямых в пространствеСкачать

Билеты №1 и №2 "Монохроматические волны"Скачать

Лампа обратной волныСкачать

§8.1 Общее уравнение прямой на плоскостиСкачать

Раскрытие тайн электромагнитной волныСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Уравнение прямой в пространстве. 11 класс.Скачать

УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

образование стоячих волнСкачать
Уравнение параллельной прямойСкачать