- Урок 6
- Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач
- Угол наклона прямой и угловой коэффициент прямой
- Уравнение с угловым коэффициентом
- Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
- Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
- Love Soft
- Инструменты пользователя
- Инструменты сайта
- Боковая панель
- Навигация
- Связь
- Содержание
- Уравнение прямой
- (I) Общее уравнение прямой на плоскости
- (II) Уравнение прямой с угловым коэффициентом
- (III) Уравнение прямой в отрезках на осях
- (IV) Уравнение прямой, проходящей через две точки
- (V) Каноническое уравнение прямой
- (VI) Параметрическое уравнение прямой
- (VII) Уравнение прямой в полярных координатах
- Калькулятор
- Переход к другой форме записи
- От общего уравнения к уравнению с угловым коэффициентом
- От уравнения с угловым коэффициентом к общему уравнению
- Угловой коэффициент прямой
- Угол между двумя прямыми
- Условие параллельности двух прямых
- Задача
- Задача
- Условие перпендикулярности двух прямых
- Задача
- Задача
- Сводная таблица
- Задачи — угловой коэффициент на бумаге в клетку
- Расстояние от точки до прямой
- 🌟 Видео
Урок 6
уравнение Прямой с угловым коэффициентом.
уравнение Прямой, Проходящей через данную точку и имеющей данный угловой коэффициент.
уравнение Прямой, Проходящей через две данные точки.
Уравнение Прямой с угловым коэффициентом.
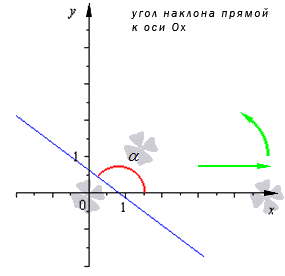
Пусть дана некоторая Прямая, не ПерПендикулярная оси ох. назовем углом наклона данной Прямой к оси ох угол а, на который нужно Повернуть ось ох, чтобы Положительное наПравление совПало с одним из наПравлений Прямой. угол а может Принимать различные значения, которые отличаются друг от друга на величину ± NП, где N — натуральное число. как Правило, в качестве угла наклона берут наименьшее неотрицательное значение угла а, на который нужно Повернуть (Против часовой стрелки) ось ох, чтобы ее Положительное наПравление совПало с одним из наПравлений Прямой. в этом случае 0
Тангенс угла наклона Прямой к оси ох называют угловым коэффициентом этой Прямой и обозначают буквой k: k= tgа (1) . из данного равенства следует, что если а=0, т.е. Прямая Параллельна оси ох, то k=0. если а=П/2, т.е. Прямая ПерПендикулярна к оси ох, то выражение k= tgа теряет смысл. в таком случае говорят, что угловой коэффициент «обращается в бесконечность».
Выведем уравнение данной Прямой, если известны ее угловой коэффициент k и величина b отрезка ов, который она отсекает на оси оу.
Пусть м — Произвольная точка Плоскости с координатами х и у. Проведем Прямые вN и Nм, Параллельные координатным осям, и Получим Прямоугольный треугольник вNм.
точка м лежит на Прямой тогда и только тогда, когда величины Nм и вN удовлетворяют условию: Nм / вN =tgа .
но Nм=см-сN=см-ов=у-b, вN=х. отсюда, учитывая формулу (1), Получаем, что точка м(х;у) лежит на данной Прямой тогда и только тогда, когда ее координаты удовлетворяют уравнению (у-b) / х=k, которое После Преобразований Примет вид у=kх+b (2) .
уравнение (2) называют уравнением Прямой с угловым коэффициентом . если k=0, то Прямая Параллельна оси ох и ее уравнение имеет вид у=b.
итак, уравнение любой Прямой, не ПерПендикулярной оси ох, имеет вид (2). очевидно, верно и обратное: любое уравнение вида (2) оПределяет Прямую, имеющую угловой коэффициент k и отсекающую на оси оу отрезок, величина которого b.
Пример 1 . составить уравнение Прямой, отсекающей на оси оу отрезок b=3 и образующий с осью ох угол а=п/4.
Решение. находим угловой коэффициент: k= tgа = tgа/ 4=1. Подставив k и b в равенство (2), Получим искомое уравнение Прямой: у=1х+3 или у-х-3=0.
Пример 2. Построить Прямую, заданную уравнением у=0,75х+2.
решение. отложим на оси оу отрезок ов, величина которого равна 2, Проведем через точку в Параллельно оси ох отрезок, величина которого вN=4, и через точку N Параллельно оси оу отрезок, величина которого Nм=3 (т.к. 0,75=3 / 4).
После этого Проводим Прямую вм, которая и является искомой. она имеет данный угловой коэффициент k=0,75=3 /4 и отсекает на оси оу отрезок величины b=2.
Уравнение Прямой, Проходящей через данную точку и имеющей данный угловой коэффициент.
в ряде случаев возникает необходимость составить уравнение Прямой, зная одну ее точку м 1 (х 1 ;у 1 ) и угловой коэффициент k . заПишем уравнение Прямой в виде (2), где b – Пока не известное число. так как Прямая Проходит через точку м 1 (х 1 ;у 1 ), то координаты этой точки удовлетворяют уравнению (2): у 1 = k х 1 + b . выразим из этого равенства b и Подставим его в уравнение (2), Получим искомое уравнение: у-у 1 = k (х – х 1 ) (3).
замечание. если Прямая Проходит ПерПендикулярно оси ох, т.е. ее угловой коэффициент обращается в бесконечность, то уравнение имеет вид х – х 1 =0. формально это уравнение можно Получить из уравнения (3), если разделить обе части уравнения (3) на k и затем устремить k к бесконечности.
Пример 3. составить уравнение Прямой, Проходящей через точку м(2;1) и образующий с осью ох угол а=45 0 .
решение. найдем угловой коэффициент: k = tgа = tg 45 0 =1. Подставим координаты точки м и значение углового коэффициента k в равенство (3), Получим уравнение Прямой: у-1=х-2 или у-х+1=0.
уравнение Прямой, Проходящей через две данные точки.
Пусть даны две точки м 1 (х 1 ;у 1 ) и м 2 (х 2 ;у 2 ). Приняв в уравнении (3) точку м(х;у) за м 2 (х 2 ;у 2 ), имеем у 2 – у 1 = k (х 2 – х 1 ). выразим из Последнего равенства k и Подставим его в уравнение (3), Получаем искомое уравнение:
это уравнение При условии, что у 1 не равен у 2 , можно заПисать так: (4)
если у 1 =у 2 , то уравнение искомой Прямой имеет вид у=у 1 . в этом случае Прямая Параллельна оси ох. если х 1 =х 2 , то Прямая Параллельна оси оу и ее уравнение имеет вид х=х 1 .
Пример 4. составить уравнение Прямой, Проходящей через точки а(3;1) и в(5;4).
решение. Подставив координаты точек а и в в равенство (4), Получаем искомое уравнение Прямой: = или 3х – 2у – 7 =0.
Автор: Вяликова Мария Владимировна — учитель математики и информатики высшей квалификационной категории МАОУ Пролетарская СОШ Новгородского района Новгородской области
Видео:Коэффициент угла наклона прямойСкачать
Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач
Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Видео:Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Угол наклона прямой и угловой коэффициент прямой
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.
Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.
Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.
Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .
Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .
Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .
Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .
Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .
Ответ: α = a r c t g 3 .
Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .
Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:
α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .
Ответ: 5 π 6 .
Видео:Угловой коэффициент прямойСкачать

Уравнение с угловым коэффициентом
Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .
Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.
Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.
Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.
Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.
Ответ: М 1 принадлежит прямой, а М 2 нет.
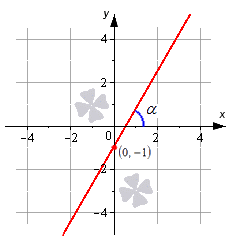
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .
Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .
Видео:Уравнение прямой по рисунку. #математика #уравнение #прямая #алгебра #наклон #точка #simplemathСкачать

Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .
Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .
Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .
Решение
По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .
Ответ: y = — 2 x + 7 .
Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .
По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:
y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3
Ответ: x 1 = y — 12 — 3 .
Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.
Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0
Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .
Решим задачу обратную данной.
Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .
Результат и является уравннием с угловым коэффициентом, который равняется — A B .
Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .
Ответ: y = 1 6 x + 1 4 .
Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:
x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1
Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.
Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:
y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .
Ответ: y = 3 2 x — 3 .
Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.
Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:
5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x
Ответ: y = 5 2 x — 6 .
Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .
Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:
x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1
Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Love Soft
Инструменты пользователя
Инструменты сайта
Боковая панель
Навигация

Связь
Содержание
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Уравнение прямой
Прямая — ГМТ, равноудаленных от двух точек.
(I) Общее уравнение прямой на плоскости
Уравнение прямой имеет вид $Ax + By + C = 0$, где $A$, $B$ и $C$ — некоторые числа, причем $A$ и $B$ не равны 0 одновременно.
При $A=0$ прямая параллельна оси oX, при $B=0$ — параллельна оси oY.
При $C=0$ прямая проходит через начало координат.
Вектор с координатами $(A;B)$ называется нормальным вектором, он перпендикулярен прямой.
Также уравнение можно переписать в виде $$A(x-x_0) + B(y-y_0) = 0$$
(II) Уравнение прямой с угловым коэффициентом
Уравнением вида $y = kx + b$ можно задать не любую прямую — а именно, нельзя задать прямую, перпендикулярную оси абсцисс.
(III) Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках $$frac x a + frac = 1$$
В этом виде невозможно представить прямую, проходящую через начало координат.
(IV) Уравнение прямой, проходящей через две точки
Пусть даны две несовпадающие точки A(x1;y1) и B(x2;y2). Уравнение прямой, проходящей через точки A(x1;y1) и B(x2;y2) имеет вид:
(V) Каноническое уравнение прямой
Если известны координаты точки $P(x_0, y_0)$ лежащей на прямой и направляющего вектора $ vec v = (a; b)$, то уравнение прямой можно записать в каноническом виде, используя следующую формулу:
(VI) Параметрическое уравнение прямой
Параметрические уравнения прямой могут быть записаны следующим образом $$ x = a t + x_0, y = b t + y_0$$ где $(x_0, y_0)$ — координаты точки лежащей на прямой, $(a, b)$ — координаты направляющего вектора прямой.
(VII) Уравнение прямой в полярных координатах
Уравнение прямой с углом наклона $alpha$ в полярных координатах $r$ и $phi$: $$r cos(phi-alpha)=p$$
Калькулятор

Видео:Как найти тангенс угла наклона?Скачать

Переход к другой форме записи
От общего уравнения к уравнению с угловым коэффициентом
Выразить переменную y: $Ax + By + C = 0$
$y = -frac A B x- frac C B$
От уравнения с угловым коэффициентом к общему уравнению
Перенести все члены в левую часть уравнения
Видео:Углы наклона прямой к плоскостям (метод дополнительных плоскостей)Скачать

Угловой коэффициент прямой
Угловой коэффициент прямой $k$ = численно равен тангенсу угла между прямой и положительным направлением оси абсцисс.
Тангенс угла может рассчитываться как отношение противолежащего катета к прилежащему.
Slope — угловой коэффициент — наклон, склон холма, показатель насколько крутой холм или гора.
Чтобы найти наклон между двумя точками на плоскости используется формула:
Иногда горизонтальное изменение называют «пробег», а вертикальное изменение — «подъем» или «снижение, спад».
Наклон биссектрисы первого координатного угла равен 1, так как скорость изменения по оси X и по оси Y одинаковы.
Например, найдем наклон между точками (2, 1) и (-9, 7)
Найдем наклон между точками (-1, -3) и (1, 1)
Чем больше модуль числа, чем круче склон. Положительное число означает, что наклон идет вверх при движении слева направо (прямая возрастает). Отрицательное число означает, что наклон идет вниз при движении слева направо (прямая убывает).
Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Угол между двумя прямыми
Пусть две неперпендикулярные прямые представляются уравнениями $$y= a_1 x+ b_1 \ y= a_2 x+ b_2$$ Тогда угол между двумя прямыми найдется по формуле $$tg(θ)=frac$$
Условие параллельности двух прямых
Две прямые параллельны (или совпадают), если равны их угловые коэффициенты.
Теорема. Прямые $y = k_1 x + b_1$ и $y = k_2 x + b_2$ параллельны тогда и только тогда, когда $k_1 = k_2$ и $b_1 ne b_2$.
Задача
Проверить, выполняется ли условие параллельности прямых $2x-3y+1=0$ и $4x-6y-5=0$.
Задача
Составить уравнение прямой линии, проходящей через точку $(1;2)$ параллельно прямой $2x-3y+1=0$.
Условие перпендикулярности двух прямых
Условие перпендикулярности прямых заключается в том, что произведение их угловых коэффициентов равно –1: $$k_1 cdot k_2=-1$$
Задача
При каком значении $k$ уравнение $y=kx+1$ определяет прямую, перпендикулярную к прямой $y=2x-1$?
Задача
Составить уравнение прямой линии, проходящей через точку $(-1;1)$ перпендикулярно к прямой $3x-y+2=0$.
Сводная таблица
| угловые коэффициенты | прямые |
|---|---|
| Если угловые коэффициенты двух линейных функций равны, то прямые, являющиеся их графиками, параллельны | Параллельные прямые имеют одинаковый наклон. |
| Если угловые коэффициенты двух линейных функций не равны, то прямые, являющиеся их графиками, пересекаются | Если прямые пересекаются, то их наклоны не равны |
| Если произведение угловых коэффициентов равно (-1), то прямые, являющиеся их графиками, перпендикулярны. | Если прямые перпендикулярны, то произведение их наклонов всегда = -1. |
| — | Если прямая параллельна оси ординат, то формула не применима (возникает деление на 0), и для таких прямых угловой коэффициент не определён. |
Видео:Уравнение прямой с угловым коэффициентомСкачать

Задачи — угловой коэффициент на бумаге в клетку
Определить угловой коэффициент прямой:
Видео:Угловой коэффициент прямойСкачать

Расстояние от точки до прямой
Когда прямая на плоскости задана уравнением $ax + by + c = 0$, где a, b и c — такие вещественные константы, что a и b не равны нулю одновременно, и расстояние от прямой до точки $(x_0,y_0)$ равно
Точка на прямой, наиболее близкая к $(x_0,y_0)$, имеет координаты
🌟 Видео
Составляем уравнение прямой по точкамСкачать

Тангенс угла наклона касательной к графику функции в точкеСкачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Математика без Ху!ни. Уравнение касательной.Скачать

Прямая и уравнение прямойСкачать

Уравнение прямой линии с угловым коэффициентом проходящей через точкуСкачать

Видеоурок "Параметрические уравнения прямой"Скачать