Продолжаем изучение раздела «Уравнение прямой на плоскости» и в этой статье разберем тему «Уравнение прямой в отрезках». Последовательно рассмотрим вид уравнения прямой в отрезках, построение прямой линии, которая задается этим уравнением, переход от общего уравнения прямой к уравнению прямой в отрезках. Все это будет сопровождаться примерами и разбором решения задач.
- Уравнение прямой в отрезках – описание и примеры
- Приведение общего уравнения прямой к уравнению прямой в отрезках
- Уравнение прямой
- Уравнение прямой на плоскости
- Уравнение прямой с угловым коэффициентом
- Уравнение прямой в отрезках на осях
- Уравнение прямой, проходящей через две различные точки на плоскости
- Параметрическое уравнение прямой на плоскости
- Каноническое уравнение прямой на плоскости
- Уравнение прямой в пространстве
- Уравнение прямой, проходящей через две различные точки в пространстве
- Параметрическое уравнение прямой в пространстве
- Каноническое уравнение прямой в пространстве
- Прямая как линия пересечения двух плоскостей
- аписать уравнение прямой, проходящей через точку А (-2;8) и середину отрезка MN, где М (6; -5), N (-2; 1), используя каноническое уравнение.
- 🎬 Видео
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Уравнение прямой в отрезках – описание и примеры
Пусть на плоскости расположена прямоугольная система координат O x y .
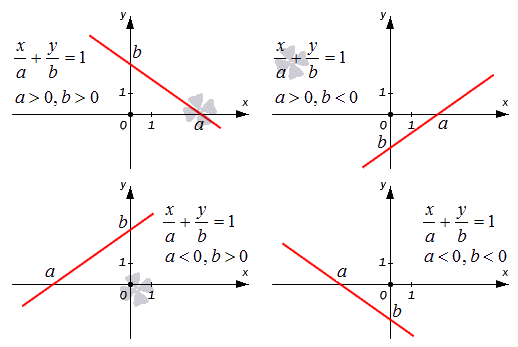
Прямая линия на плоскости в декартовой системе координат O x y задается уравнением вида x a + y b = 1 , где a и b – это некоторые действительные числа, отличные от нуля, величины которых равны длинам отрезков, отсекаемых прямой линией на осях O x и O y . Длины отрезков считаются от начала координат.
Как мы знаем, координаты любой из точек, принадлежащих прямой линии, заданной уравнением прямой, удовлетворяют уравнению этой прямой. Точки a , 0 и 0 , b принадлежат данной прямой линии, так как a a + 0 b = 1 ⇔ 1 ≡ 1 и 0 a + b b = 1 ⇔ 1 ≡ 1 . Точки a , 0 и b , 0 расположены на осях координат O x и O y и удалены от начала координат на a и b единиц. Направление, в котором нужно откладывать длину отрезка, определяется знаком, который стоит перед числами a и b . Знак « — » обозначает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.
Поясним все вышесказанное, расположив прямые относительно фиксированной декартовой системы координат O x y на схематическом чертеже. Уравнение прямой в отрезках x a + y b = 1 применяется для построения прямой линии в декартовой системе координат O x y . Для этого нам необходимо отметить на осях точки a , 0 и b , 0 , а затем соединить эти точки линией при помощи линейки.
На чертеже показаны случаи, когда числа a и b имеют различные знаки, и, следовательно, длины отрезков откладываются в разных направлениях координатных осей.
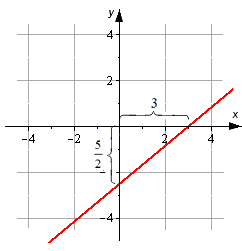
Прямая линия задана уравнением прямой в отрезках вида x 3 + y — 5 2 = 1 . Необходимо построить эту прямую на плоскости в декартовой системе координат O x y .
Решение
Используя уравнение прямой в отрезках, определим точки, через которые проходит прямая линия. Это 3 , 0 , 0 , — 5 2 . Отметим их и проведем линию.
Видео:Координаты середины отрезкаСкачать
Приведение общего уравнения прямой к уравнению прямой в отрезках
Переход от заданного уравнения прямой к уравнению прямой в отрезках облегчает нам решение различных задач. Имея полное общее уравнение прямой, мы можем получить уравнение прямой в отрезках.
Полное общее уравнение прямой линии на плоскости имеет вид A x + B y + C = 0 , где А , В и C не равны нулю. Мы переносим число C в правую часть равенства, делим обе части полученного равенства на – С . При этом, коэффициенты при x и y мы отправляем в знаменатели:
A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1
Для осуществления последнего перехода мы воспользовались равенством p q = 1 q p , p ≠ 0 , q ≠ 0 .
В результате, мы осуществили переход от общего уравнения прямой A x + B y + C = 0 к уравнению прямой в отрезках x a + y b = 1 , где a = — C A , b = — C B .
Разберем следующий пример.
Осуществим переход к уравнению прямой в отрезках, имея общее уравнение прямой x — 7 y + 1 2 = 0 .
Решение
Переносим одну вторую в правую часть равенства x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .
Делим обе части равенства на — 1 2 : x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .
Преобразуем полученное равенство к нужному виду: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .
Мы получили уравнение прямой в отрезках.
Ответ: x — 1 2 + y 1 14 = 1
В тех случаях, когда прямая линия задана каноническим или параметрическим уравнением прямой на плоскости, то сначала мы переходим к общему уравнению прямой, а затем уже к уравнению прямой в отрезках.
Перейти от уравнения прямой в отрезках и общему уравнению прямой осуществляется просто: мы переносим единицу из правой части уравнения прямой в отрезках вида x a + y b = 1 в левую часть с противоположным знаком, выделяем коэффициенты перед неизвестными x и y .
x a + y b = 1 ⇔ x a + y b — 1 = 0 ⇔ 1 a · x + 1 b · y — 1 = 0
Получаем общее уравнение прямой, от которого можно перейти к любому другому виду уравнения прямой на плоскости. Процесс перехода мы подробно разобрали в теме «Приведение общего уравнения прямой к другим видам уравнения прямой».
Уравнение прямой в отрезках имеет вид x 2 3 + y — 12 = 1 . Необходимо написать общее уравнение прямой на плоскости.
Решение
Действует по заранее описанному алгоритму:
x 2 3 + y — 12 = 1 ⇔ 1 2 3 · x + 1 — 12 · y — 1 = 0 ⇔ ⇔ 3 2 · x — 1 12 · y — 1 = 0
Ответ: 3 2 · x — 1 12 · y — 1 = 0
Видео:9 класс, 7 урок, Уравнение прямойСкачать
Уравнение прямой
Видео:№160. Прямая а проходит через середину отрезка АВ и перпендикулярна к нему. Докажите, что: а) каждаяСкачать
Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках
| x | + | y | = 1 |
| a | b |
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
| x — x 1 | = | y — y 1 |
| x 2 — x 1 | y 2 — y 1 |
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x 0 y = m t + y 0
где N( x 0, y 0) — координаты точки лежащей на прямой, a = — координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a = ( l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x — x 0 | = | y — y 0 |
| l | m |
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x — 1 2 — 1 = y — 7 3 — 7
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
x = t + 1 y = -4 t + 7
Решение. Так как M y — N y = 0, то невозможно записать уравнение прямой проходящей через две точки.
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Видео:Расстояние между двумя точками. Координаты середины отрезка.Скачать
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
| x — x 1 | = | y — y 1 | = | z — z 1 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
 | x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
где ( x 0, y 0, z 0) — координаты точки лежащей на прямой, — координаты направляющего вектора прямой.
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n = , то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x — x 0 | = | y — y 0 | = | z — z 0 |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
Видео:Построение середины отрезкаСкачать
аписать уравнение прямой, проходящей через точку А (-2;8) и середину отрезка MN, где М (6; -5), N (-2; 1), используя каноническое уравнение.
Координаты середины векторов вычисляются по формуле:
— где C — координата середины, К — конца, Н — начала:
Пусть середина MN — С, тогда:
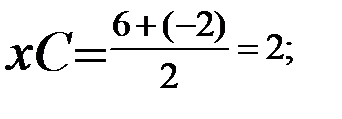
Данные точки лежат на одной прямой. Через систему уравнений найдём коэффициенты k и b данной прямой y=kx+b, подставив в неё координаты точек:
8 = -2k+b 8 = -2k-2-2k 4k =-10 k = -2,5
-2 = 2k+b b = -2-2k b =-2-2k b = 3
Для полученной прямой y = -2,5x+3 приведём уравнение:
2. Найти пределы:
а) 
б) 
а) 
= 
= 
=
= 
= 
= 2
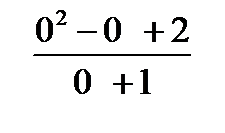
б) =
Разделим числитель и знаменатель на х 3
= 
=
Сделаем замену: u=1/x
= 
= 
= — 
3. Найти интегралы:
а) 
; б) 
; в) 
.
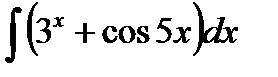
а) = 
— 
+ 
= 
— 
+ 3x + C
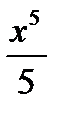
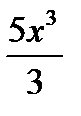
б) = 8 
= 8 ln x + C
в) =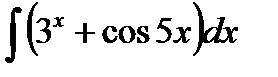 
+ 
= 
+
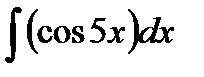
Тогда пусть du=5dx и подставим dx=du/5:
+ = + 
= + sin(u)+C= + sin(5x)+C
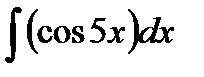
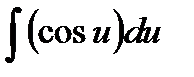
4. Исследовать функцию и построить график: у = 3х 3 – х
Точки пересечения с осью координат Y
График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в 3х 3 – х.
3⋅ 0 3 − 0=0
Точки пересечения с осью координат X
График пересекает ось X, когда y равняется 0:
подставляем y = 0 в y=3x 3 — x.
3 x 3 −x =0
x2= 
x3=- 
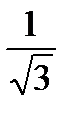
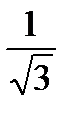
Точки: (0, 0); ( ,0); ( — ,0).
Для того, чтобы найти экстремумы, нужно решить уравнение
f ′(x)=0 (производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
f ′(x)=( 3 x 3 −x)′ = 9x 2 – 1
9x 2 – 1 = 0
Решаем это уравнение, получаем:
x1=−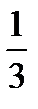 
;
x2= 
.
Значит экстремумы в точках: (− ; 
); ( ; — 
)
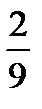
Интервалы возрастания и убывания функции.
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимум функции в точке x1= ;
Максимум функции в точке x2=− .
Убывает на промежутках ( — ∞; − ] U [∞; )
Возрастает на промежутке [− ; ]
Найдем точки перегибов, для этого надо решить уравнение
f ′′(x)=0 (вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции,
f ′′(x)= (3 x 3 −x)′′= (9x 2 – 1)′ = 18x
Решаем это уравнение, получаем:
Интервалы выпуклости и вогнутости.
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках
[0, ∞)
Выпуклая на промежутках
(-∞, 0]
Горизонтальные асимптоты найдём с помощью пределов данной функции при x→∞ и x→ — ∞
(3x 3 -x)= — ∞ значит,
горизонтальной асимптоты слева не существует.
(3x 3 -x)= ∞ значит,
горизонтальной асимптоты справа не существует.
Наклонную асимптоту можно найти, подсчитав предел функции 3x 3 -x, делённой на x при x→∞ и x→ — ∞
= ∞ значит,
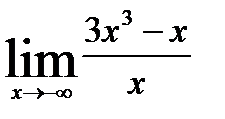
наклонной асимптоты слева не существует.
= ∞ значит,
наклонной асимптоты справа не существует.
Чётность и нечётность функции
Проверим чётность и нечётность функции с помощью соотношений
f = f(-x) и f = -f(-x).
Итак, проверяем:
3x 3 -x = -3x 3 +x Нет
3x 3 -x = -(-3x 3 +x) Нет
значит, функция не является ни чётной, ни нечётной.
5.Решить дифференциальное уравнение:
у(0)=5
Представим исходное дифференциальное уравнение в виде:
или 
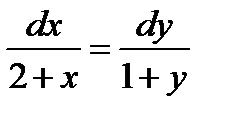
Интегрируя обе части, получаем:
Тогда решением дифференциального уравнения будет
🎬 Видео
Координаты середины отрезка. Формула. Геометрия 9 класс.Скачать
Построение середины отрезкаСкачать
Видеоурок "Уравнение прямой в отрезках"Скачать
Аналитическая геометрия, 6 урок, Уравнение прямойСкачать
Записать уравнение прямой параллельной или перпендикулярной данной.Скачать
Длина отрезкаСкачать
Координаты середины отрезка. Уравнение средней линии или диагонали. Урок 4. Геометрия 8 класс.Скачать
УРАВНЕНИЕ ПРЯМОЙСкачать
№276. Через середину отрезка проведена прямая. Докажите, что концы отрезка равноудалены от этойСкачать
Уравнения стороны треугольника и медианыСкачать
8 класс. Координаты середины отрезка. Расстояние между точками. Уравнение окружности. КонтрольнаяСкачать
Координаты середины отрезка. Практическая часть. 11 класс.Скачать
Геометрия Задача- Ловушка Help Найти середину отрезка циркулемСкачать
Геометрия 9 класс. Тема: "Уравнение прямой".Скачать
