Видео:§28 Эксцентриситет эллипсаСкачать

Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:

где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Видео:165. Найти фокусы и эксцентриситет эллипса.Скачать

Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как 

Каноническое уравнение эллипса имеет вид:

где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка 

Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид 
Пример 1. Проверить, является ли линия, заданная общим уравнением 
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:

Точки 


называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет 
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением 
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

Получаем фокусы эллипса:
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет 
Видео:Эллипс (часть 8). Решение задач. Высшая математика.Скачать

Продолжаем решать задачи на эллипс вместе
Если 



Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями

называются директрисами эллипса (на чертеже — красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса

где 



Пример 7. Дан эллипс 
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. 

Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки 

Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:

Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка 

Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:

Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.

так как из исходного уравнения эллипса 
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Видео:Фокусы эллипсаСкачать

Кривые второго порядка на плоскости
Уравнение вида Ах 2 +2Вху+Су 2 +2Dх+2Еу+F=0 называется общим уравнением кривой второго порядка. Коэффициенты уравнения – действительные числа, причем хотя бы одно из чисел А,В,С отлично от нуля. Такое уравнение определяет на плоскости окружность, эллипс, гиперболу или параболу.
В табл. 2 приведены уравнения кривых второго порядка и определен смысл входящих в них коэффициентов.
| № п/п | Определение кривой | Вид уравнения | Примечание | |||||
 Эллипс – множество всех точек плоскости, сумма расстояний от которых до двух точек, называемых фокусами, есть величина постоянная (рис.4) Эллипс – множество всех точек плоскости, сумма расстояний от которых до двух точек, называемых фокусами, есть величина постоянная (рис.4) |  — каноническое уравнение эллипса — каноническое уравнение эллипса | 2а – большая ось; 2b – малая ось 2с–межфокус-ное расстояние с 2 =а 2 -b 2 ; 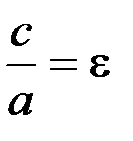 — эксцентриси-тет, 0 2 =а 2 +b 2 ; — эксцентриси-тет, 0 2 =а 2 +b 2 ; 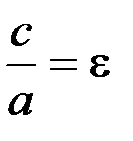 — эксцентри-ситет, e>1. Точки А1,А2 – вершины гиперболы. Прямые — эксцентри-ситет, e>1. Точки А1,А2 – вершины гиперболы. Прямые 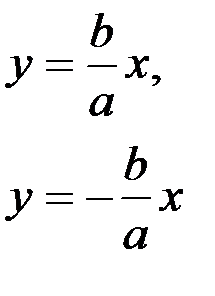 — асимптоты — асимптоты | ||||||
| 3. | Парабола — множество точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директриссой.
| у 2 =2px – каноническое уравнение параболы, симметричной относительно оси ОХ x 2 =2pу – каноническое уравнение параболы, симметричной относительно оси ОY (рис.6б) | F  — фокус, — фокус, 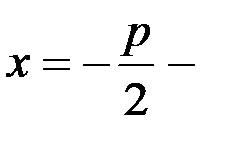 ди-ректриса. Точка (0;0) – вершина параболы (рис.6а) F ди-ректриса. Точка (0;0) – вершина параболы (рис.6а) F  — фокус, — фокус,  ди-ректриса. Точка (0;0) – вершина параболы (рис.6б) ди-ректриса. Точка (0;0) – вершина параболы (рис.6б) |
1. Найти координаты фокусов и эксцентриситет эллипса 36х 2 +100у 2 =3600.
Приведем уравнение эллипса к каноническому виду:
36х 2 +100у 2 =3600, поделим обе части уравнения на 3600:

С= 
Эксцентриситет: 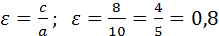
Ответ: Fл(-8,0); Fп(8,0); 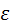
2.Написать уравнение прямой, проходящей через левую вершину эллипса 16х 2 +25у 2 =400 и точку М0(1;-3) (рис.7).
| у |
Решение:
| -4 |
| -5 |
| М |
| х |
| М0 |
| Рис. 7 |
Приведем уравнение 16х 2 +25у 2 =400 к каноническому виду.
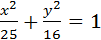
Левая вершина эллипса (-а,0)Þ(-5,0). Обозначим М(-5,0). Составим уравнение прямой, проходящей через точки М0 и М:
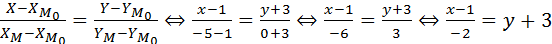
Ответ: 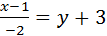
3. Написать уравнение прямой, проходящей через правый фокус гиперболы 9х 2 -16у 2 =144 и параллельно прямой 3х-2у+6=0 (рис.8).
| -3 |
| -4 |
| FП |
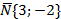 |
| х |
| у |
| Рис.8 |
Приведем уравнение 9х 2 -16у 2 =144 к каноническому виду 
Правый фокус гиперболы Fп(с,0);
С= 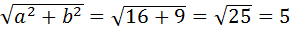
Пусть уравнение искомой прямой имеет вид y=k2x+b2;
Значит, y=(3/2)x+b2 проходит через точку Fп(5,0), то 0=(3/2)5+b2Þb2=-15/2. Итак, 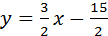
Искомая прямая проходит через точку Fл(5,0) параллельно прямой 3х-2у+6=0. Из общего уравнения заданной прямой определяем вектор нормали 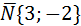
4. Написать уравнение прямой l, проходящей через нижнюю вершину эллипса 4х 2 +20у 2 =80, перпендикулярно прямой 2х—у+1=0 (рис.9).
| М |
 |
| -2 |
| y |
 |
| l |
| х |
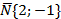 |
| Рис. 9 |
Приведем уравнение к каноническому виду 4х 2 +20у 2 =80,
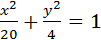
Нижняя вершина имеет вид: М(0;-b)=М(0;-2).
Условие перпендикулярности двух прямых: k1k3=-1.
k2=-1: k1Þk2=-1/2,
Так как прямая 

Итак, 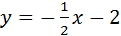
По условию задачи требуется написать уравнение прямой l, проходящей через точку М(0;-2) перпендикулярно прямой 2х—у+1=0. Из общего уравнения прямой определяем координаты вектора нормали 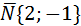
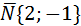
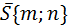

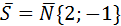

5. Написать уравнение прямой, проходящей через правый фокус эллипса 
Правый фокус эллипса имеет вид Fп(с,0);
С= 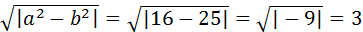
Так как прямая проходит под углом 45˚ к оси Ох, то k=tgα=tg45˚=1.
Пусть уравнение искомой прямой имеет вид: y=kx+b;
Так как прямая проходит через точку Fп(3,0), то 0=3+bÞb=-3.
Плоскость в пространстве
Любое уравнение первой степени в трехмерном пространстве определяет какую-либо плоскость.
Разным способам задания плоскости соответствуют различные виды уравнений (табл. 3.)
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечание |
| Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору А(х-х0)+В(у-у0)+С(z-z0)=0 | (x0,y0,z0) – координаты заданной точки; АВС – координаты заданного вектора | Вектор N(А,В,С) называется нормальным вектором плоскости | |
| Общее уравнение плоскости Ах+Ву+Сz+D=0 | D=-Ax0-By0-Cz0, АВС – нормальный вектор плоскости; | Это уравнение получается из уравнения (1) эле-ментарными | |
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечание |
| х0,y0,z0 – координаты данной точки | преобразованиями | ||
Уравнение плоскости, проходящей через три заданные точки 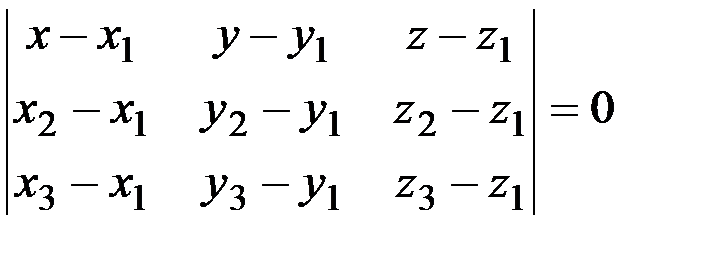 | М1(х1,y1,z1), М2(х2,y2,z2), М3(х3,y3,z3) – три точки, заданные своими координатами | Точки М1, М2, М3 не должны лежать на одной прямой | |
Уравнение плоскости в отрезках на осях 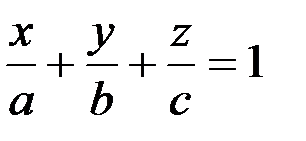 | а,b,c – отрезки, отсекаемые плоскостью от осей координат | аbc≠0 |
Пусть даны две плоскости a1 и a2:
Угол между двумя плоскостями определяется как 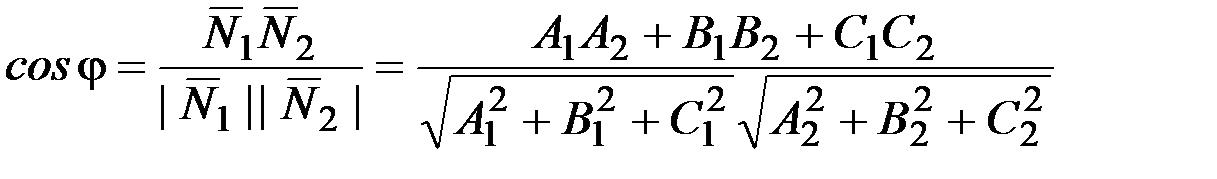
Условие перпендикулярности двух плоскостей:
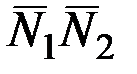
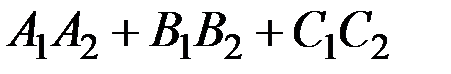
Условие параллельности двух плоскостей:


Расстояние от точки до плоскости:
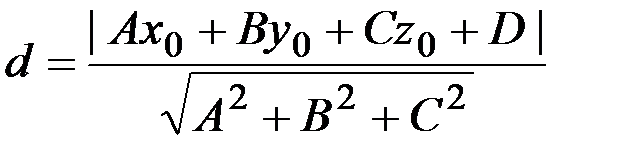
Видео:213. Фокус и директриса параболы.Скачать

Курс высшей математики (стр. 4 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 |

Теорема. Для того, чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.
Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением:
1) Координаты нижней вершины: x = 0; y2 = 16; y = -4.
2) Координаты левого фокуса: c2 = a2 – b2 = 25 – 16 = 9; c = 3; F2(-3; 0).
3) Уравнение прямой, проходящей через две точки:
Пример. Составить уравнение эллипса, если его фокусы F1(0; 0), F2(1; 1), большая ось равна 2.
Уравнение эллипса имеет вид: 
2c = 
по условию 2а = 2, следовательно а = 1, b =
Итого: 
Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.

По определению ïr1 – r2ï= 2a. F1, F2 – фокусы гиперболы. F1F2 = 2c.
Выберем на гиперболе произвольную точку М(х, у). Тогда:
обозначим с2 – а2 = b2 (геометрически эта величина – меньшая полуось)
Получили каноническое уравнение гиперболы.
Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.
Ось 2а называется действительной осью гиперболы.

Гипербола имеет две асимптоты, уравнения которых
Определение. Отношение 
С учетом того, что с2 – а2 = b2:
Если а = b, e = 


Теорема. Если r – расстояние от произвольной точки М гиперболы до какого — либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.
Доказательство. Изобразим схематично гиперболу.

Из очевидных геометрических соотношений можно записать:
a/e + d = x, следовательно d = x – a/e.
Из канонического уравнения: 
Тогда т. к. с/a = e, то r = ex – a.
Итого: 
Для левой ветви гиперболы доказательство аналогично. Теорема доказана.
Пример. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса 
Для эллипса: c2 = a2 – b2.
Для гиперболы: c2 = a2 + b2.
 |
Уравнение гиперболы: 
Пример. Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением
Находим фокусное расстояние c2 = 25 – 9 = 16.
Для гиперболы: c2 = a2 + b2 = 16, e = c/a = 2; c = 2a; c2 = 4a2; a2 = 4;
Итого: 
Определение. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.
Расположим начало координат посередине между фокусом и директрисой.


 |
 |
Величина р (расстояние от фокуса до директрисы) называется параметром параболы. Выведем каноническое уравнение параболы.
Из геометрических соотношений: AM = MF; AM = x + p/2;
MF2 = y2 + (x – p/2)2
(x + p/2)2 = y2 + (x – p/2)2
x2 +xp + p2/4 = y2 + x2 – xp + p2/4
Уравнение директрисы: x = — p/2.
Пример. На параболе у2 = 8х найти точку, расстояние которой от директрисы равно 4.
Из уравнения параболы получаем, что р = 4.
r = x + p/2 = 4; следовательно:
x = 2; y2 = 16; y = ±4. Искомые точки: M1(2; 4), M2(2; -4).
Любая точка на плоскости может быть однозначно определена при помощи различных координатных систем, выбор которых определяется различными факторами. Способ задания начальных условий для решения какой – либо конкретной технической задачи может определить выбор той или иной системы координат. Для удобства проведения вычислений часто предпочтительнее использовать системы координат, отличные от декартовой прямоугольной системы. Кроме того, наглядность представления окончательного ответа зачастую тоже сильно зависит от выбора системы координат. Ниже рассмотрим некоторые наиболее часто используемые системы координат.
Полярная система координат.
Определение. Точка О называется полюсом, а луч l – полярной осью.
Суть задания какой — либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. В случае полярной системы координат роль этих чисел играют расстояние точки от полюса и угол между полярной осью и радиус– вектором этой точки. Этот угол j называется полярным углом.
 |
r =
Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси Ох.
Тогда координаты произвольной точки в двух различных системах координат связываются соотношениями:
Пример. Уравнение кривой в полярной системе координат имеет вид:

Воспользуемся связью декартовой прямоугольной и полярной системы координат: 
Получили каноническое уравнение эллипса. Из уравнения видно, что центр эллипса сдвинут вдоль оси Ох на 1/2 вправо, большая полуось a равна 3/2, меньшая полуось b равна 

—
Пример. Уравнение кривой в полярной системе координат имеет вид:

Подставим в заданное уравнение формулы, связывающие полярную и декартову прямоугольную системы координат.
Получили каноническое уравнение гиперболы. Из уравнения видно, что гипербола сдвинута вдоль оси Ох на 5 влево, большая полуось а равна 4, меньшая полуось b равна 3, откуда получаем c2 = a2 + b2 ; c = 5; e = c/a = 5/4.
Фокусы F1(-10; 0), F2(0; 0).
Построим график этой гиперболы.
 |
Аналитическая геометрия в пространстве.
Уравнение линии в пространстве.
Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:
Это уравнение называется уравнением линии в пространстве.
Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана каким — либо уравнением.
Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 – уравнения поверхностей, пересекающихся по линии L.
Тогда пару уравнений
назовем уравнением линии в пространстве.
Уравнение прямой в пространстве по точке и
Возьмем произвольную прямую и вектор 

На прямой возьмем две произвольные точки М0(x0, y0, z0) и M(x, y, z).


Обозначим радиус — векторы этих точек как 









Итого, можно записать: 


Т. к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.
Это векторное уравнение может быть представлено в координатной форме:
Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве:

Определение. Направляющими косинусами прямой называются направляющие косинусы вектора 


Отсюда получим: m : n : p = cosa : cosb : cosg.
Числа m, n, p называются угловыми коэффициентами прямой. Т. к. 
Уравнение прямой в пространстве, проходящей
через две точки.
Если на прямой в пространстве отметить две произвольные точки M1(x1, y1, z1) и M2(x2, y2, z2), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:

Кроме того, для точки М1 можно записать:



Это уравнение прямой, проходящей через две точки в пространстве.
Общие уравнения прямой в пространстве.
Уравнение прямой может быть рассмотрено как уравнение линии пересечения двух плоскостей.
Как было рассмотрено выше, плоскость в векторной форме может быть задана уравнением:




Пусть в пространстве заданы две плоскости: 






Тогда общие уравнения прямой в векторной форме:
Общие уравнения прямой в координатной форме:
Практическая задача часто состоит в приведении уравнений прямых в общем виде к каноническому виду.
Для этого надо найти произвольную точку прямой и числа m, n, p.
При этом направляющий вектор прямой может быть найден как векторное произведение векторов нормали к заданным плоскостям.
Пример. Найти каноническое уравнение, если прямая задана в виде:
Для нахождения произвольной точки прямой, примем ее координату х = 0, а затем подставим это значение в заданную систему уравнений.

Находим компоненты направляющего вектора прямой.
Тогда канонические уравнения прямой:
Пример. Привести к каноническому виду уравнение прямой, заданное в виде:
Для нахождения произвольной точки прямой, являющейся линией пересечения указанных выше плоскостей, примем z = 0. Тогда:

Получаем: A(-1; 3; 0).
Направляющий вектор прямой: 
Итого:
Угол между плоскостями.
 |
Угол между двумя плоскостями в пространстве j связан с углом между нормалями к этим плоскостям j1 соотношением: j = j1 или j = 1800 — j1, т. е.
Определим угол j1. Известно, что плоскости могут быть заданы соотношениями:




Таким образом, угол между плоскостями находится по формуле:
Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.
Условия параллельности и перпендикулярности
На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей.






Угол между прямыми в пространстве.
Пусть в пространстве заданы две прямые. Их параметрические уравнения:
l1:
l2:
Угол между прямыми j и угол между направляющими векторами j этих прямых связаны соотношением: j = j1 или j = 1800 — j1. Угол между направляющими векторами находится из скалярного произведения. Таким образом:

Условия параллельности и перпендикулярности
прямых в пространстве.
Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т. е. их соответствующие координаты были пропорциональны.
Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т. е. косинус угла между ними равен нулю.
Угол между прямой и плоскостью.
Определение. Углом между прямой и плоскостью называется любой угол между прямой и ее проекцией на эту плоскость.

Пусть плоскость задана уравнением 



В координатной форме:
Условия параллельности и перпендикулярности
прямой и плоскости в пространстве.
Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.
Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарны. Это условие выполняется, если векторное произведение этих векторов было равно нулю.
Поверхности второго порядка.
Определение. Поверхности второго порядка – это поверхности, уравнения которых в прямоугольной системе координат являются уравнениями второго порядка.
Определение. Цилиндрическими поверхностями называются поверхности, образованные линиями, параллельными какой — либо фиксированной прямой.
Рассмотрим поверхности, в уравнении которых отсутствует составляющая z, т. е. направляющие параллельны оси Оz. Тип линии на плоскости ХOY (эта линия называется направляющей поверхности) определяет характер цилиндрической поверхности. Рассмотрим некоторые частные случаи в зависимости от уравнения направляющих:
1) 
2) 
 |
2) x2 = 2py – параболический цилиндр.
 |
Определение. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращения с осью вращения d.
Если уравнение поверхности в прямоугольной системе координат имеет вид:
F(x2 + y2, z) = 0, то эта поверхность – поверхность вращения с осью вращения Оz.
Аналогично: F(x2 + z2, y) = 0 – поверхность вращения с осью вращения Оу,
F(z2 + y2, x) = 0 – поверхность вращения с осью вращения Ох.
Запишем уравнения поверхностей вращения для некоторых частных случаев:
1) 
2) 
3) 
4) 
Аналогично могут быть записаны уравнения для рассмотренных выше поверхностей вращения, если осью вращения являются оси Ох или Оу.
Однако, перечисленные выше поверхности являются всего лишь частными случаями поверхностей второго порядка общего вида, некоторые типы которых рассмотрены ниже:
Сфера:
 |
Трехосный эллипсоид:
В сечении эллипсоида плоскостями, параллельными координатным плоскостям, получаются эллипсы с различными осями.
 |
Однополостный гиперболоид:
 |
Двуполостный гиперболоид:
 |
Эллиптический параболоид:
 |
Гиперболический параболоид:
 |
Конус второго порядка:
📹 Видео
ЭллипсСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

11 класс, 52 урок, ЭллипсСкачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Фокус и директриса параболы 1Скачать

Овчинников А. В. - Аналитическая геометрия - Эллипс, гипербола, параболаСкачать

Аналитическая геометрия: окружность и эллипсСкачать
Определить тип кривой (эллипс)Скачать

Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Эллипс. Гипербола. Их вырожденияСкачать

169. Фокальные расстояния точки эллипса.Скачать

































































































