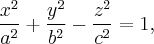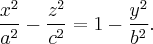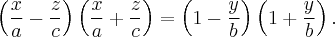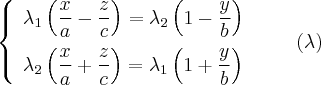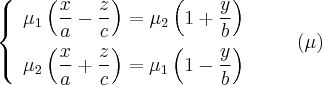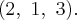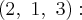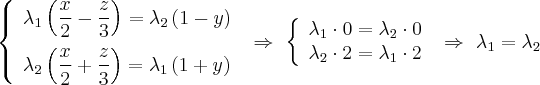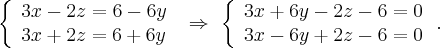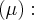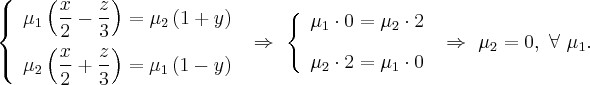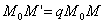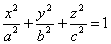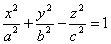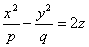Уравнение прямолинейных образующих однополостного гиперболоида через точку (7 видео)

Прямолинейные образующие на поверхности однополостного гиперболоида

Уравнение однополостного гиперболоида имеет вид:

Разложим на множители:

Рассмотрим следующую систему линейных уравнений:

Каждое линейное уравнение задает в пространстве плоскость. Данные плоскости не параллельны, следовательно эта система из двух линейных уравнений задает прямую. Покажем, что эта прямая лежит на Однополостный гиперболоид. Действительно, если точка принадлежит этой прямой, то она удовлетворяет каждое из линейных уравнений системы, следовательно удовлетворяет произведения этих уравнений, то есть уравнению однополостного гиперболоида.

Это утверждение справедливо для любых 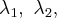которые не равны нулю одновременно. Итак, мы получили уравнение одной семьи прямолинейных образующих на Однополостный гиперболоид.

Уравнение второй семьи :

Теорема. Однополостный гиперболоид несет на себе две семьи прямолинейных образующих, имеющих следующие свойства:

· через любую точку проходит ровно одна прямая с каждой семьи ;

· любые две образующие из разных семей лежат в одной плоскости;

· любые две образующие с одной семьи является скрещивающимися;

· любые три образующие с одной семьи не параллельны одной плоскости.

Доказательство можно посмотреть в методичке.

Пример. Найти прямолинейные образующие поверхности 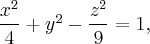которые проходят через точку

Запишем уравнение первой семьи прямолинейных образующих 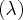и подставим координаты точки

Можем взять любые числа, удовлетворяющие этому равенства, например: 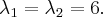Получаем уравнение прямолинейной образующей с первой семьи :

Уравнение второй семьи

Возьмем, 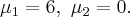получаем уравнение прямолинейной образующей с другойсемье :

Содержание

121. Однополостные гиперболоиды и его прямолинейные образующие
Уравнение прямолинейных образующих однополостного гиперболоида через точку
Глава 46. Поверхности второго порядка
📹 Видео

Видео:Лекция. Гиперболоиды, параболоиды, конус. Исследование методом сечений.Скачать

121. Однополостные гиперболоиды и его прямолинейные образующие

Определение 1. Поверхность, которая в некоторой прямоугольной системе координат имеет уравнение

, (10)

Называется Однополостным гиперболоидом, A > 0, B > 0, C > 0. Числа A, B, C называются Полуосями однополостным гиперболоидом.

Исследуем поверхность однополостного гиперболоида по уравнению (10). Так как все переменные входят в уравнение (10) в четной степени, то вместе с точкой (X, Y, Z) однополостному гиперболоиду принадлежат все восемь точек (±X, ±Y, ±Z) (с произвольными комбинациями знаков). Таким образом, однополостной гиперболоид симметричен относительно, всех трех координатных плоскостей и начала координат. Он пересекает координатные оси OX, OY соответственно в точках (±A, 0, 0), (0, ±B, 0), которые называются Вершинами Однополостного гиперболоида.

Видео:Образование поверхностей перемещением кривых, 1973Скачать

Уравнение прямолинейных образующих однополостного гиперболоида через точку

Видео:Поверхности 2-го порядка | Лекция 14 | ЛинАл | СтримСкачать

Глава 46. Поверхности второго порядка

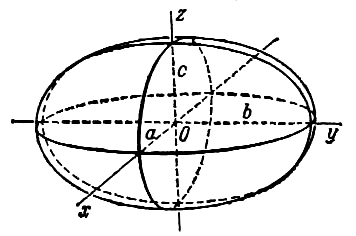
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

(1).

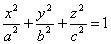
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.

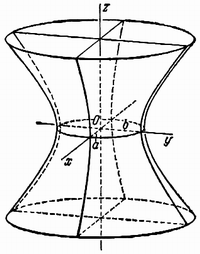
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (2)

. (3)

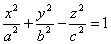
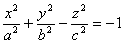
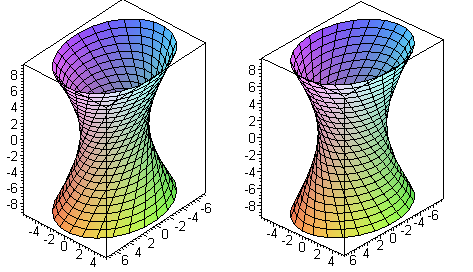
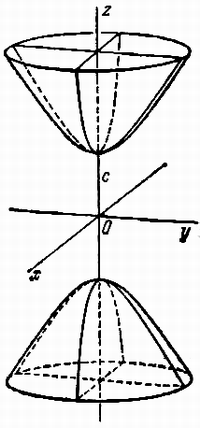
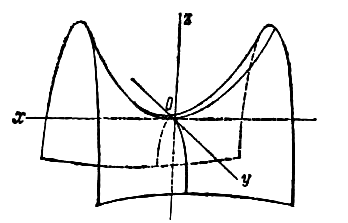
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

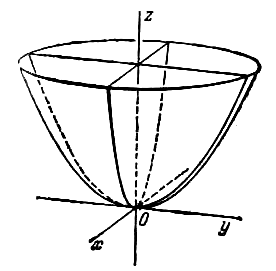
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (4)

, (5)

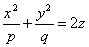
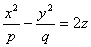
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

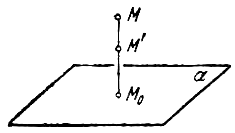
Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).

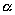
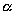
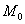
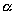
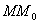
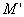
Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости , — основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство

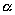
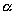
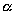
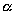
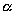
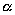
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.

Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).

ПРИМЕР. Доказать, что произвольный трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .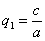

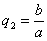
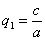
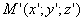
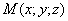
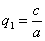
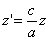
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть — точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .

Таким образом, мы получаем искомые выражения:

, , (6)

, , (7)

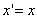
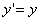
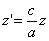
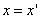
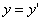
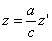
Предположим, что M(x; y; z ) — произвольная точка сферы

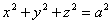
Заменим здесь x, y, z их выражениями (7); получим

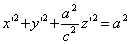
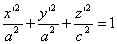
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам

, , ;

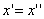
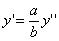
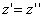
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.

Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.

имеет две системы прямолинейных образующих, которые определяются уравнениями:

, ;

, ,

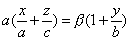
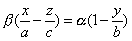
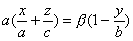
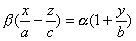
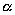
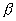
где и — некоторые числа, не равные одновременно нулю. Гиперболический параболоид

также имеет две системы прямолинейных образующих, которые определяются уравнениями

, ;

, .

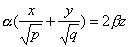
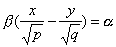
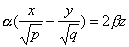
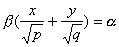
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.

Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).