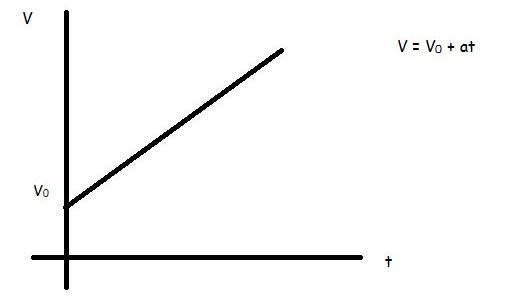Уравнение прямолинейного движения с постоянным ускорением (4 видео)

Уравнение прямолинейного движения с постоянным ускорением

§ 5. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ С ПОСТОЯННЫМ УСКОРЕНИЕМ: УРАВНЕНИЕ ДЛЯ СКОРОСТИ И ПРОЙДЕННОГО ПУТИ

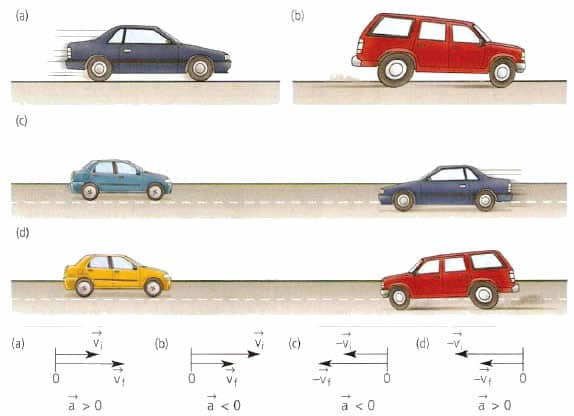
Прямолинейное движение с постоянным ускорением называют равноускоренным, если модуль скорости увеличивается со временем, или равнозамедленным, если он уменьшается.

Примером ускоренного движения может быть падение цветочного горшка с балкона невысокого дома. В начале падения скорость горшка равна нулю, но за несколько секунд она успевает вырасти до десятков м/с. Примером замедленного движения является движение камня, брошенного вертикально вверх, скорость которого сначала большая, но потом постепенно уменьшается до нуля в верхней точке траектории. Если пренебречь силой сопротивления воздуха, то ускорение в обоих этих случаях будет одинаково и равно ускорению свободного падения, которое всегда направлено вертикально вниз, обозначается буквой g и равно примерно 9,8 м/с 2 .

Ускорение свободного падения, g вызвано силой притяжения Земли. Эта сила ускоряет все тела, движущиеся по направлению к земле, и замедляет те, которые движутся от неё.

Чтобы найти уравнение для скорости при прямолинейном движении с постоянным ускорением, будем считать, что в момент времени t =0 тело имело начальную скорость v ₀ . Так как ускорение a постоянно, то для любого момента времени t справедливо следующее уравнение:

Уравнение прямолинейного движения с постоянным ускорением

где v – скорость тела в момент времени t , откуда после нетрудных преобразований получаем уравнение для скорости при движении с постоянным ускорением:

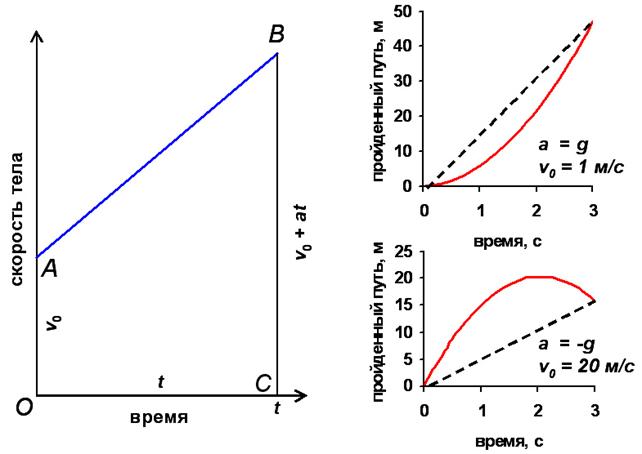
Чтобы вывести уравнение для пути, пройденного при прямолинейном движении с постоянным ускорением, построим сначала график зависимости скорости от времени (5.1). Для a >0 график этой зависимости изображён слева на рис.5 (синяя прямая). Как мы установили в §3, перемещение, совершённое за время t , можно определить, если вычислить площадь под кривой зависимости скорости от времени между моментами t =0 и t . В нашем случае фигура под кривой, ограниченная двумя вертикальными линиями t =0 и t , представляет собой трапецию OABC , площадь которой S , как известно, равна произведению полусуммы длин оснований OA и CB на высоту OC :

Как видно на рис.5, OA = v ₀ , CB = v ₀ + at , а OC = t . Подставляя эти значения в (5.2), получаем следующее уравнение для перемещения S , совершённого за время t при прямолинейном движении с постоянным ускорением a при начальной скорости v ₀ :

Легко показать, что формула (5.3) справедлива не только для движения с ускорением a >0, для которого она была выведена, но и в тех случаях, когда a S при положительных (верх) и отрицательных (низ) значениях a , построенные по формуле (5.3) для различных величин v ₀ . Видно, что в отличие от равномерного движения (см. рис. 3), график зависимости перемещения от времени является параболой, а не прямой, показанной для сравнения пунктирной линией.

Вопросы для повторения:

· Является ли движение с постоянным ускорением равномерным?

· Дайте определение равноускоренного и равнозамедленного движения.

· Чему равно ускорение свободного падения, и чем оно вызвано?

· По какому закону изменяется скорость при равноускоренном или равнозамедленном движении?

· Как зависит перемещение при равноускоренном движении от времени, ускорения и начальной скорости?

Рис. 5. Слева – зависимость скорости от времени (синяя прямая) при равноускоренном движении; справа – зависимости перемещения от времени (красные кривые) при равноускоренном (верх) и равнозамедленном движении (низ).

Содержание

Уравнение прямолинейного движения с постоянным ускорением
Примеры решения задач на движение с постоянным ускорением
Понятие об ускорении. Движение с постоянным ускорением по прямой линии. Формулы и решение задачи
Понятие об ускорении
Скорость при движении с постоянным ускорением
Формулы пройденного пути
Решение задачи
📸 Видео

Видео:Уравнение движения с постоянным ускорением | Физика 10 класс #6 | ИнфоурокСкачать

Уравнение прямолинейного движения с постоянным ускорением

Кинематика — это просто!

В общем случае движение может быть криволинейным и неравномерным.
Тогда вектор скорости будет меняться и по направлению, и по величине, а это значит, что тело движется с ускорением.
Ускорение показывает быстроту изменения скорости.

Ускорение — это векторная величина, которая характеризуется модулем и направлением.

Единица измерения ускорения в системе СИ:

Частным случаем такого движения является прямолинейное движение с постоянным ускорением.
Постоянное ускорение — это когда ускорение не меняется ни по модулю, ни по направлению.

Прямолинейное движение с постоянным ускорением подразделяется на:
1. равноускоренное, когда при движении модуль скорости тела увеличивается (тело разгоняется).
Здесь векторы скорости и ускорения совпадают по направлению.

2. равнозамедленное, когда при движении модуль скорости тела уменьшается (тело тормозит).
Здесь векторы скорости и ускорения направлены противоположно друг другу.

Формула ускорения:
1. в векторном виде

2. расчетная формула в координатной форме (для решения задач)

Отсюда «вытекает» уравнение скорости, которое выражает мгновенную скорость тела в любой момент времени:
1. в векторном виде

2. расчетная формула в координатной форме

Графики ускорения

Перемещение

1. формула перемещения в векторном виде

2. Расчетная формула в координатной форме

Графики перемещения

Уравнение движения (или иначе уравнение координаты)

1. в векторном виде

2. расчетная формула в координатной форме

Примеры решения задач на движение с постоянным ускорением

Задача 1

Тело движется согласно уравнению х=2-4t-2t 2 .
Дать описание движения тела.
Составить уравнение скорости движущегося тела.
Определить скорость тела и координату через 10 секунд после начала движения.

Решение

Сравниваем заданное уравнение движения х=2-4t-2t 2 с формулой:

По полученным данным даем описание движения тела:

— тело движется из точки с координатами 2 метра относительно начала координат с начальной скоростью 4 м/с противоположно направлению координатной оси ОХ с постоянным ускорением 4 м/с 2 , разгоняется, т.к. направление вектора скорости и вектора ускорения совпадают.

Составляем уравнение скорости, глядя на расчетную формулу для скорости:

Расчитываем скорость и координату тела через 10 секунд после начала движения:

Задача 2

Уравнение движения тела x=-3+t+t 2
Дать описание движения тела.
Определить скорость и координату тела через 2 секунды после начала движения.

Решение

Рассуждаем аналогично вышерассмотренной задаче:

Тело движется из точки с координатами -3 метра относительно начала координат с начальной скоростью 1 м/с в направлении координатной оси ОХ с постоянным ускорением 2м/с 2 , разгоняется, т.к. проекции вектора скорости и ускорения имеют одинаковые знаки, значит оба векторв направлены одинаково.

Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Понятие об ускорении. Движение с постоянным ускорением по прямой линии. Формулы и решение задачи

Изучением классического механического движения в физике занимается кинематика. В отличие от динамики, наука изучает, почему движутся тела. Она отвечает на вопрос, как они это делают. В данной статье рассмотрим, что такое ускорение и движение с постоянным ускорением.

Видео:Ускорение. Движение с постоянным ускорением. Единица ускорения | Физика 10 класс #5 | ИнфоурокСкачать

Понятие об ускорении

Когда тело движется в пространстве, за некоторое время оно преодолевает определенный путь, который является длиной траектории. Чтобы рассчитать этот путь, пользуются понятиями скорости и ускорения.

Скорость как физическая величина характеризует быстроту во времени изменения пройденного пути. Скорость направлена по касательной к траектории в сторону перемещения тела.

Вам будет интересно: Что такое «пис», где возникло, как употребляется?

Ускорение — это несколько более сложная величина. Говоря кратко, она описывает изменение скорости в рассматриваемый момент времени. Математическое определение ускорения выглядит так:

Чтобы яснее понять эту формулу, приведем простой пример: предположим, что за 1 секунду движения скорость тела увеличилась на 1 м/с. Эти цифры, подставленные в выражение выше, приводят к результату: ускорение тела в течение этой секунды было равно 1 м/с2.

Направление ускорения совершенно не зависит от направления скорости. Его вектор совпадает с вектором результирующей силы, которая вызывает это ускорение.

Следует отметить важный момент в приведенном определении ускорения. Эта величина характеризует не только изменение скорости по модулю, но и по направлению. Последний факт следует учитывать в случае криволинейного движения. Далее в статье будет рассматриваться только прямолинейное движение.

Видео:(16.09) §10 Движение с постоянным ускорениемСкачать

Скорость при движении с постоянным ускорением

Ускорение является постоянным, если оно в процессе движения сохраняет свой модуль и направление. Такое движение называют равноускоренным или равнозамедленным — все зависит от того, приводит ли ускорение к увеличению скорости или к ее уменьшению.

В случае движения тела с постоянным ускорением определить скорость можно по одной из следующих формул:

Первые два уравнения характеризуют равноускоренное перемещение. Отличие между ними заключается в том, что второе выражение применимо для случая ненулевой начальной скорости.

Третье уравнение — это выражение для скорости при равнозамедленном движении с постоянным ускорением. Ускорение при этом направлено против скорости.

Графиками всех трех функций v(t) являются прямые. В первых двух случаях прямые имеют положительный наклон относительно оси абсцисс, в третьем случае этот наклон является отрицательным.

Видео:Урок 24. Мгновенная скорость. Равноускоренное движение. УскорениеСкачать

Формулы пройденного пути

Для пути в случае движения с ускорением постоянным (ускорение a = const) получить формулы несложно, если вычислить интеграл от скорости по времени. Проделав эту математическую операцию для записанных выше трех уравнений, мы получим следующие выражения для пути L:

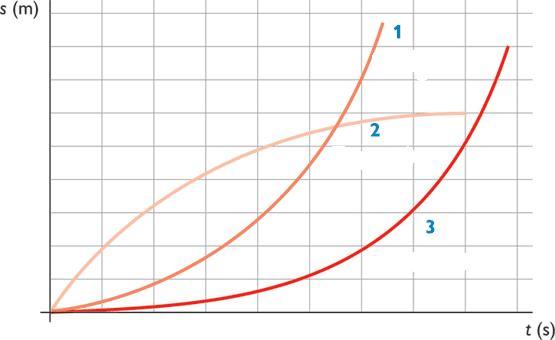
Графиками всех трех функций пути от времени являются параболы. В первых двух случаях правая ветвь параболы возрастает, а для третьей функции она постепенно выходит на некоторую константу, которая соответствует пройденному пути до полной остановки тела.

Видео:Прямолинейное равноускоренное движение. Ускорение | Физика 9 класс #5 | ИнфоурокСкачать

Решение задачи

Двигаясь со скоростью 30 км/ч, автомобиль начал ускоряться. За 30 секунд он прошел расстояние 600 метров. Чему было равно ускорение автомобиля?

В первую очередь переведем начальную скорость из км/ч в м/с:

v0 = 30 км/ч = 30000/3600 = 8,333 м/с.

Теперь запишем уравнение движения:

Из этого равенства выразим ускорение, получим:

Все физические величины в этом уравнении известны из условия задачи. Подставляем их в формулу и получаем ответ: a ≈ 0,78 м/с2. Таким образом, двигаясь с ускорением постоянным, автомобиль за каждую секунду увеличивал свою скорость на 0,78 м/с.

Рассчитаем также (для интереса), какую скорость он приобрел через 30 секунд ускоренного движения, получаем:

v = v0 + a*t = 8,333 + 0,78*30 = 31,733 м/с.