Уравнение процессов и их графиков (6 видео)

Изопроцессы — виды графиков, формулы законов и уравнения

Содержание

Трактовка понятий
Уравнение процессов и их графиков
А теперь к задачам!
Блог об энергетике
энергетика простыми словами
Основные термодинамические процессы
Изохорный процесс
Изобарный процесс
Изотермический процесс
Адиабатный процесс
Политропный процесс
📹 Видео

Видео:Решение графических задач на тему Газовые законыСкачать

Трактовка понятий

Газ является одним из существующих агрегатных состояний вещества, для которого характерна слабая связь между компонентами и большая подвижность частиц. Последние передвигатся хаотично и свободно. При их столкновения изменяется характер движения.

Реальный газ считается высоко перегретым паром. Его свойства несколько отличаются от идеального компонента. В термодинамики различаются два состояния:

насыщенные пары либо системы с двумя фазами;
перегретые пары либо однофазовые системы.

Газы, как и жидкости, обладают текучестью. Они хорошо сопротивляются деформации. В отличие от воды, газ не имеет фиксированного объёма. Он стремится заполнить весь сосуд. Изопроцессы в газах подчиняются законам, которые определяют зависимость между двумя параметрами вещества при постоянном значении третьего. Так как уравнение справедливо для любой смеси, поэтому формула изотермического процесса (ИЗ) выражается следующим образом: T=const.

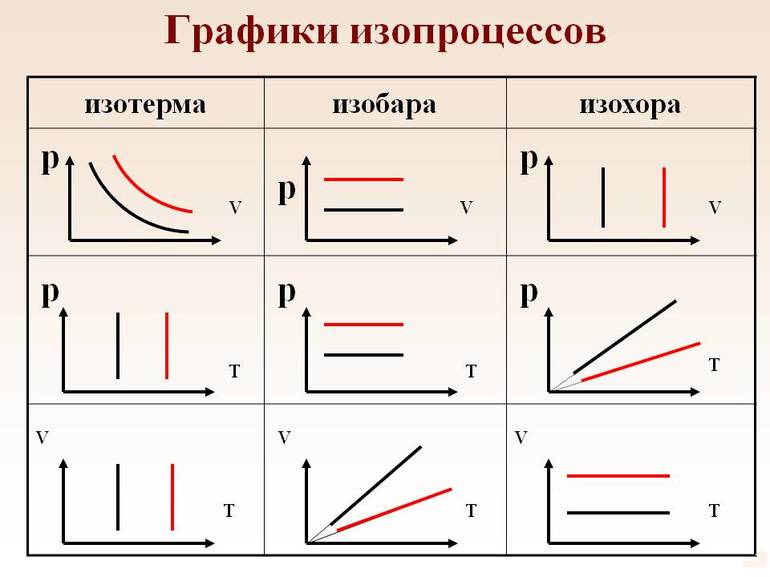
Само понятие ИЗ трактуется как новое состояние вещества, которое протекает при неизменной температуре. Процесс соответствует закону Бойля — Мариотта: для газа определённой массы произведение объёма на давление постоянно, если не изменяется температура. Равенство отображается на графике изопроцессов с помощью гиперболы и координат. Отдельно отмечаются изотермы при разных значениях температуры. В последнем случае соблюдается неравенство: Т1 23 молекул. Это считается числом Авогадро.

По закону Дальтона, давление смеси равно сумме парциальных P, входящих в состав. Выражение записывается следующим образом: P cm=P1+P2+…Pn. Последний показатель Pn является давлением газа, который бы занимал весь объёмом сосуда.

Чаще в старших классах физике рассматриваются изохорические процессы, когда переходит идеальный газ из одного состояния в другое, при этом не изменяется его объёмом. Явление впервые рассмотрел француз Жак Шарль. Закон записывается следующим образом: PV=vRT. Так как v= const и V=const, поэтому для любых разных состояний веществ используется равенство: P1/T1=P2/T2=….Pn/Tn. Закон Шарля математически записывается так: P/T=const.

Из выражения следует, что между температурой и давлением наблюдается прямо пропорциональная связь. Если увеличивается P, тогда повышается T, и наоборот. График зависимости данных величин называется изохорой. На промежутке абсолютного нуля для кривых предусмотрена условная зависимость. Прямая доводится до начала координат с помощью пунктирных линий.

Подобная зависимость T от P и V при изобарных и изохорных процессах определяет точность и эффективность измерения температуры газовыми термометрами. Первыми ученые открыли эти явления, которые считаются частными случаями уравнения состояния. Позже физики утвердили закон Клапейрона и Менделеева.

Если следовать хронологии, сначала изучались процессы, которые протекали при постоянной температуре, а затем при одном объеме. Последними рассматривались изобарические процессы. Редким и интересным явлением считается изоэнтропия, когда изменяется термодинамическая система при условии постоянной энтропии. Последнее записывается как S=const.

Примером подобного считается адиабатический обратимый процесс. Чтобы вычислить идеальный газ, используется уравнение: pV γ = const, где γ — показатель адиабаты (определяется типом газа). Для адиабатического явления характерно отсутствие теплоприёма и теплоотдачи. Физики считают такие процессы быстро протекающими.

Видео:Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

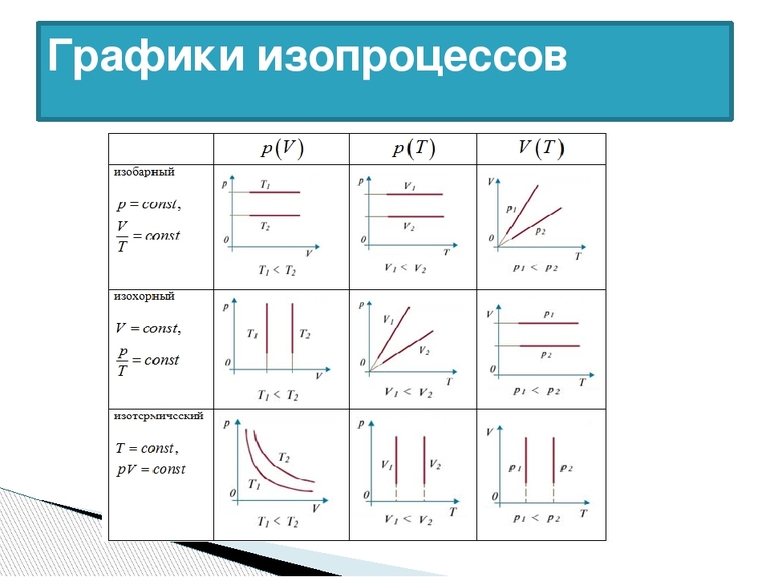
Уравнение процессов и их графиков

Задачи по физике — это просто!

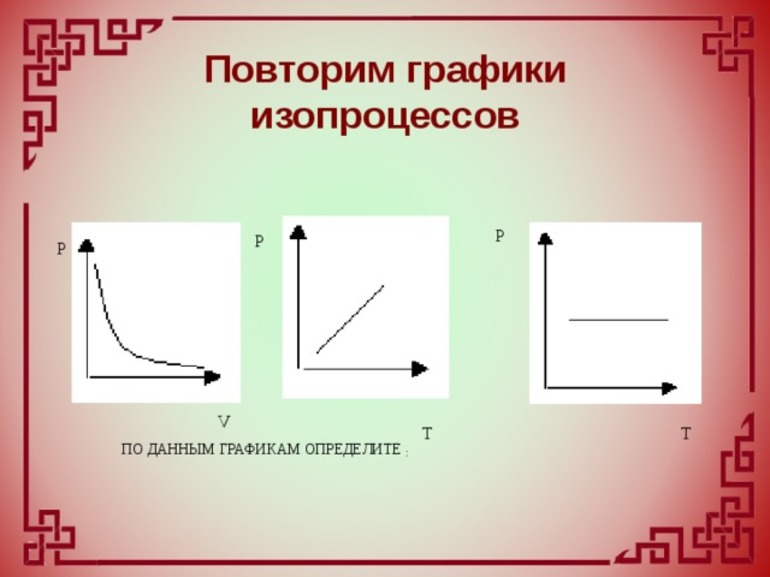
Вспомним

Изопроцессы — это термодинамические процессы при неизменной массе и постоянном значении одного из параметров.
1. Изотерический процесс описывается законом Бойля-Мариотта.

Выше представлены изотермы (графики изменения параметров газа при изотермическом процессе) в разных координатных осях.
(х)1 — начальное состояние газа
(х)2 — последующее состояние газа
Стрелочкой на графике показывают направление перехода из состояния 1 в состояние 2.

2. Изобарный процесс описывается законом Гей-Люсака.
Ниже представлены изобары в разных координатных осях.

3. Изохорный процесс описывается законом Шарля.
Ниже представлены изохоры в разных координатных осях.

Не забываем
Решать задачи надо всегда в системе СИ!

А теперь к задачам!

Элементарные задачи из курса школьной физики по теродинамике на процессы в газах.

Задача 1

Задан процесс изменения состояния газа в координатах VОТ.
На каждом участке
1). Назвать процессы и указать законы, их описывающие, показать изенения макропарамметров газа.
2). Начертить графики изменения состояния газа в координатах pOT и pOV.

Задача 2

Задан процесс изменения состояния газа в координатах рОТ.
На каждом участке
1). Назвать процессы и указать законы, их описывающие, показать изменения макропараметров газа.
2). Начертить графики изменения состояния газа в координатах pOV и VOT.

Задача 3

Задан процесс изменения состояния газа в координатах VОТ.
На каждом участке
1). Назвать процессы и указать законы, их описывающие, показать изменения макропараметров газа.
2). Начертить графики изменения состояния газа в координатах pOT и pOV.

Задача 4

Видео:Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать

Блог об энергетике

Видео:10 класс, 16 урок, Функции y=sinx, y=cosx, их свойства и графикиСкачать

энергетика простыми словами

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Основные термодинамические процессы

Основными процессами в термодинамике являются:

изохорный, протекающий при постоянном объеме;
изобарный, протекающий при постоянном давлении;
изотермический, происходящий при постоянной температуре;
адиабатный, при котором теплообмен с окружающей средой отсутствует;
политропный, удовлетворяющий уравнению pv n = const.

Изохорный, изобарный, изотермический и адиабатный процессы являются частными случаями политропного процесса.

При исследовании термодинамических процессов определяют:

уравнение процесса в p—v иT—s координатах;
связь между параметрами состояния газа;
изменение внутренней энергии;
величину внешней работы;
количество подведенной теплоты на осуществление процесса или количество отведенной теплоты.

Изохорный процесс

При изохорном процессе выполняется условие v = const.

Из уравнения состояния идеального газа (pv = RT) следует:

т. е. давление газа прямо пропорционально его абсолютной температуре:

Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).

Количество теплоты, подведенной к рабочему телу в процессе 1-2 при c_v = const определяется по формуле:

Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:

Изменение энтропии в изохорном процессе определяется по формуле:

Изобарный процесс

Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует:

т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.

Работа будет равна:

Количество теплоты при c_p = const определяется по формуле:

Изменение энтропии будет равно:

Изотермический процесс

При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно:

т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.

Работа процесса будет равна:

Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:

При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.

Изменение энтропии равно:

Адиабатный процесс

Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как dq = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:

В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.

Обозначим теплоемкость в адиабатном процессе через c_ад, и условие dq = 0 выразим следующим образом:

Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (c_ад = 0).

и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид:

В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона).

k_{выхлопных газов ДВС} = 1,33

Из предыдущих формул следует:

Техническая работа адиабатного процесса (l_техн) равна разности энтальпий начала и конца процесса (i₁ – i₂).

Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. В T, s-диаграмме он изображается вертикальной линией.

Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае ds > 0, и процесс называется реальным адиабатным процессом.

Политропный процесс

Политропным называется процесс, который описывается уравнением:

Показатель политропы n может принимать любые значения в пределах от -∞ до +∞, но для данного процесса он является постоянной величиной.

Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p, vи Tв любых двух точках на политропе:

Работа расширения газа в политропном процессе равна:

В случае идеального газа эту формулу можно преобразовать:

Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики:

представляет собой теплоемкость идеального газа в политропном процессе.

При c_v, k и n = const c_n = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью.

Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.

Графическое представление политропа в p, v координатах в зависимости от показателя политропа n.

pv 0 = const (n = 0) – изобара;

pv = const (n = 1) – изотерма;

p 0 v = const, p 1/∞ v = const, pv ∞ = const – изохора;

n > 0 – гиперболические кривые,

n По материалам моего конспекта лекций по термодинамике и учебника «Основы энергетики». Автор Г. Ф. Быстрицкий. 2-е изд., испр. и доп. — М. :КНОРУС, 2011. — 352 с.