Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
- Уравнение состояния идеального газа
- Уравнение Клапейрона
- Изопроцессы
- Какой процесс называют изотермическим. Закон Бойля — Мариотта
- Какой процесс называют изобарным. Закон Гей-Люссака
- Закон Гей-Люссака
- Изохорный процесс. Закон Шарля
- Закон Шарля
- Пример №1
- Пример №2
- Уравнение произвольного процесса в идеальном газе массой m формула
- Тесты по теме «Уравнение Менделеева-Клапейрона»
- Краткое описание документа:
- Дистанционное обучение как современный формат преподавания
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Физика: теория и методика преподавания в образовательной организации
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 💥 Видео
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 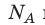
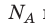
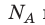
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
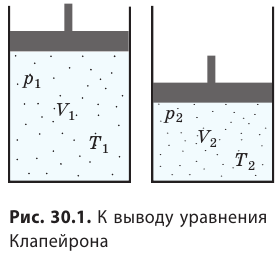
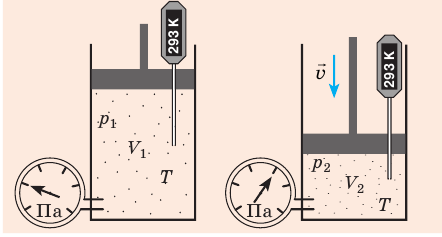
Уравнение Клапейрона
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (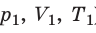
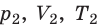
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 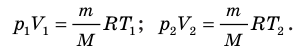
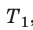
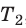
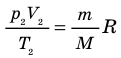
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (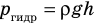
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (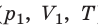
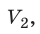
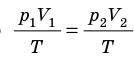
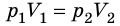
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 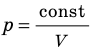
Какой процесс называют изобарным. Закон Гей-Люссака
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (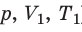
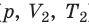
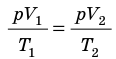
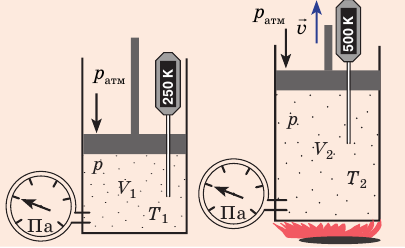
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
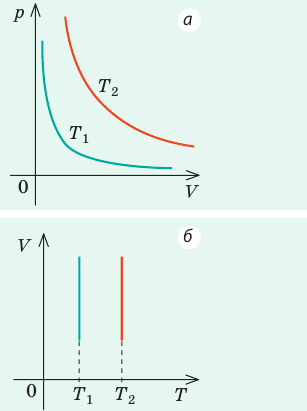
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (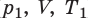
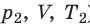
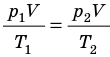
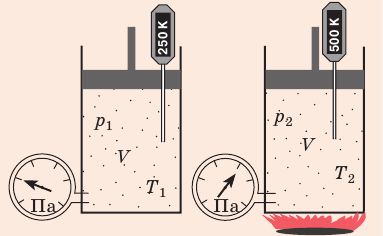
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
Пример №1
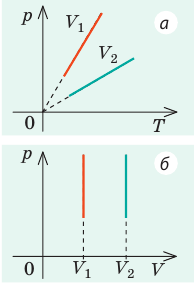
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 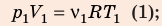
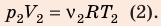

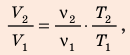
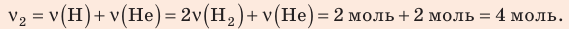
Ответ: примерно в 2,7 раза.
Пример №2
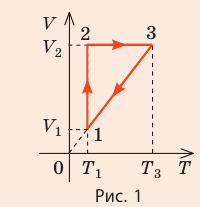
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
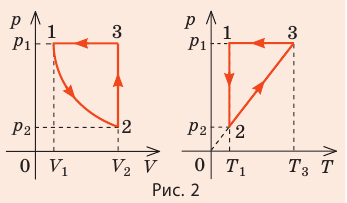
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
— универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Уравнение произвольного процесса в идеальном газе массой m формула
Уравнение Менделеева-Клапейрона — уравнение состояния для идеального газа, отнесенное к 1 молю газа. В 1874 г. Д. И. Менделеев на основе уравнения Клапейрона объединив его с законом Авогадро, используя молярный объем Vm и отнеся его к 1 молю, вывел уравнение состояния для 1 моля идеального газа:
pV = RT , где R — универсальная газовая постоянная,
R = 8,31 Дж/(моль . К)
Уравнение Клапейрона-Менделеева показывает, что для данной массы газа возможно одновременно изменение трех параметров, характеризующих состояние идеального газа. Для произвольной массы газа М, молярная масса которого m: pV = (М/m) . RT. или pV = NАkT,
где NА — число Авогадро, k — постоянная Больцмана.
С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из параметров — давление, объем или температура — остается постоянным, а изменяются только остальные два и получить теоретически газовые законы для этих условий изменения состояния газа.
Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.
Изотермический процесс — процесс изменения состояния системы при постоянной температуре. Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется. Это закон Бойля — Мариотта.
Для того, чтобы температура газа оставалась в процессе неизменной, необходимо, чтобы газ мог обмениваться теплотой с внешней большой системой — термостатом. Роль термостата может играть внешняя среда (воздух атмосферы). Согласно закону Бойля-Мариотта, давление газа обратно пропорционально его объему: P1V1=P2V2=const. Графическая зависимость давления газа от объема изображается в виде кривой (гиперболы), которая носит название изотермы. Разным температурам соответствуют разные изотермы.
Изобарный процесс — процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется. Это закон Гей-Люссака. Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const. Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные изобары. Закон Гей-Люссака не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.
Изохорный процесс — процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля. Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const. Графически эта зависимость в координатах P-Т изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изохорой. Разным объемам соответствуют разные изохоры. Закон Шарля не соблюдается в области низких температур, близких и температуре сжижения (конденсации) газов.
Итак, из закона pV = (М/m) . RT выводятся следующие законы:
p = const => V/T = const — закон Гей — Люссака .
V= const => p/T = const — закон Шарля
Если идеальный газ является смесью нескольких газов, то согласно закону Дальтона, давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов. Парциальное давление — это такое давление, которое производил бы газ, если бы он один занимал весь объем, равный объему смеси.
Некоторых, возможно, интересует вопрос, каким образом удалось определить постоянную Авогадро NA = 6,02·10 23 ? Значение числа Авогадро было экспериментально установлено только в конце XIX – начале XX века. Опишем один из таких экспериментов.
В откачанный до глубокого вакуума сосуд объемом V = 30 мл поместили навеску элемента радия массой 0,5 г и выдержали там в течение одного года. Было известно, что за секунду 1 г радия испускает 3,7·10 10 альфа-частиц. Эти частицы представляют собой ядра гелия, которые тут же принимают электроны из стенок сосуда и превращаются в атомы гелия. За год давление в сосуде выросло до 7,95·10 -4 атм (при температуре 27 о С). Изменением массы радия за год можно пренебречь. Итак, чему равна NA?
Сначала найдем, сколько альфа-частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:
N = 3,7·10 10 · 0,5 г · 60 сек · 60 мин · 24 час · 365 дней = 5,83·10 17 атомов.
Запишем уравнение Клапейрона-Менделеева PV = nRT и заметим, что число молей гелия n = N/NA. Отсюда:
NA = NRT = 5,83 . 10 17 . 0,0821 . 300 = 6,02 . 10 23
PV 7,95 . 10 -4 . 3 . 10 -2
В начале XX века этот способ определения постоянной Авогадро был самым точным. Но почему так долго (в течение года) длился эксперимент? Дело в том, что радий добывается очень трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое количество гелия может образоваться из радия только за достаточно долгое время.
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Тесты по теме «Уравнение Менделеева-Клапейрона»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
Уравнение Менделеева- Клапейрона. Газовые законы.
1. На рисунке точки 1 и 2 соответствуют термодинамическому состоянию одной и той же массы идеального газа. Каково соотношение (больше, меньше или равно) между давлениями, объемами и температурами газа в этих состояниях?
2. На рисунке точки 1 и 2 соответствуют состояниям одной и той же массы идеального газа. Установить, в каком из указанных состояний больше давление, объем, температура.
3. Воздух под поршнем насоса имел давление 10 5 Па и объем 200 см 3 . Если температура газа не изменится, то объем 130 см 3 он займет при давлении
A ) 1,5·10 4 Па B ) 1,3·10 4 Па C ) 2·10 5 Па D ) 1,5·10 5 Па E ) 2·10 4 Па
4. Состояние макроскопических тел определяется макроскопическими параметрами. К их числу относятся:
A ) Давление, объем и температура. B ) Давление, объем и молярная масса. C ) Давление, объем и универсальная газовая постоянная. D ) Масса газа, объем и температура. E ) Универсальная газовая постоянная.
5. Изобара идеального газа представлена на графике
A ) 1 B ) 2 С ) 3 D ) 4 E ) 5
6. Выражение для вычисления плотности газа
A ) pV / T B ) Mp / RT C ) pV / kT D ) pV / RT E ) pV / T
7. На рисунке показаны процесс изменения состояния идеального газа. Укажите на графике изобару
A ) на графике изобары нет
8. Чтобы давление газа увеличилось в 3 раза при постоянном объеме, его температуру надо
A ) увеличить в 4 раза B ) увеличить в 3 раза C ) уменьшить в 4 раза D ) увеличить в 
9. Газ занимает объем 2 м 3 при температуре 273ºС. Объем этого газа при температуре 546ºС и прежнем давлении равен
A) 1 м 3 B) 2 м 3 C) 3 м 3 D) 4 м 3 E) 5 м 3
10. На рисунке приведены графики изменения состояния газа. Назовите их (по порядку 1-2-3)
A 
B ) изобара, изохора, изотерма
C ) изохора, изотерма, изобара
D ) изотерма, изобара, изохора
E ) изотерма, изохора, изобара
Уравнение Менделеева- Клапейрона. Газовые законы.
1. На рисунке точки 1 и 2 соответствуют термодинамическому состоянию одной и той же массы идеального газа. Каково соотношение (больше, меньше или равно) между давлениями, объемами и температурами газа в этих состояниях?
2. На рисунке точки 1 и 2 соответствуют состояниям одной и той же массы идеального газа. Установить, в каком из указанных состояний больше давление, объем, температура.
3. Масса водорода, находящегося в баллоне вместимостью 20 литров при температуре 27ºС под давлением 831 кПа, равна (Мн2=2·10 -3 кг/моль; R =8,31 Дж/моль·К)
A ) ≈ 1,33·10 2 кг B ) ≈ 13,3·10 -3 кг C ) ≈ 0,133·10 -3 кг D ) ≈ 1,33 кг E ) ≈ 1,33·10 -3 кг
4. Процесс изменения состояния термодинамической системы при постоянном давлении
A ) не существует B ) изохорный C ) адиабатный D ) изотермический E ) изобарный
5. Изотерма идеального газа представлена на графике
1 B ) 2 С ) 3 D ) 4 E ) 5
6. В сосуде объемом V при давлении р и температуре Т может находиться ν молей идеального газа, равное
( k -постоянная Больцмана, R — газовая постоянная)
A ) 



7. На рисунке показаны процессы изменения состояния идеального газа. График изотермы
8. Если давление газа уменьшилось в 4 раза при постоянной температуре, то его объем
A ) увеличился в 2 раза B ) увеличился в 4 раза C ) уменьшился в 2 раза D ) уменьшился в 4 раза E ) не изменился
9. В цилиндре под поршнем изобарически охлаждают 10 л газа от 127 ºС до 7ºС. Объем охлажденного газа равен
A) 7 л B) 5 л C) 12 л D) 9 л E) 2 л
10. Каким процессам соответствуют графики 1-2, 2-3, 3-1
A ) изобарный, изохорный, изотермический B ) изохорный, изобарный, изотермический
С ) изотермический, изобарный, изохорный D ) изохорный, изотермический, изобарный
E ) изобарный, изотермический, изохорный
Уравнение Менделеева- Клапейрона. Газовые законы.
1. На рисунке точки 1 и 2 соответствуют термодинамическому состоянию одной и той же массы идеального газа. Каково соотношение (больше, меньше или равно) между давлениями, объемами и температурами газа в этих состояниях?
2. На рисунке точки 1 и 2 соответствуют состояниям одной и той же массы идеального газа. Установить, в каком из указанных состояний больше давление, объем, температура.
3. Температура 2 моль газа, при объеме 44,8 л и давлении 1 атм. Равна (1 атм.= 10 5 Па; R =8,31 Дж/моль·К)
A ) 100ºС B ) -3,4ºС C ) 146ºС D ) 46ºС E ) 273ºС
4. При изотермическом процессе изменяются параметры
A ) P , V , T , m B ) P , V C ) P , T D ) P , V , T E ) V , T
5. Укажите график изотермического расширения идеального газа
4 B ) 3 C ) 5 D ) 1 E ) 2
6. Укажите уравнение произвольного процесса в идеальном газе массой m (уравнение Клапейрона)
A ) 



7. На рисунке показаны процессы изменения состояния идеального газа. График изохоры
8. Чтобы при постоянном давлении газа объем газа увеличился в 2 раза, его температуру нужно
A ) увеличить в 2 раза B ) увеличить в 4 раз C ) уменьшить в 2 раза D ) оставить неизменной E ) уменьшить в 4 раза
9. При температуре 27 ºС давление газа в закрытом сосуде равнялось 75 кПа. При температуре t = -13ºС давление газа будет
A ) 20 кПа B ) 65 кПа C ) 15 кПа D ) 40 кПа E ) 35 кПа
10. На диаграмме V — T переведен график, описывающий 2 процесса в идеальном газе при переходе 1-2-3. Это процессы
A ) изобарического охлаждения и изотермического сжатия B ) изотермического нагревания и изохорического расширения C ) изобарического нагревания и изотермического расширения
D ) изобарического нагревания и изотермического сжатия E ) изобарического охлаждения и изотермического сжатия
Уравнение Менделеева- Клапейрона. Газовые законы.
1. На рисунке точки 1 и 2 соответствуют термодинамическому состоянию одной и той же массы идеального газа. Каково соотношение (больше, меньше или равно) между давлениями, объемами и температурами газа в этих состояниях?
2. На рисунке точки 1 и 2 соответствуют состояниям одной и той же массы идеального газа. Установить, в каком из указанных состояний больше давление, объем, температура.
3. Молярная масса газа 4·10 -3 кг/моль. 5 кг этого газа при температуре 500 К занимает объем 34,6 м 3 . Давление газа равно ( R =8,31 Дж/моль·К)
A ) 1400 кПа B ) 150 кПа C ) 16 кПа D ) 255 кПа E ) 1,45 кПа
4. Процессы, протекающие при неизменном значении одного из параметров, характеризующих состояние идеального газа, называются
A ) конвекционными B ) диффузными C ) равновесными D ) дифракционными E ) изопроцессами
5. Укажите график изохорного нагревания идеального газа
A ) 4 B ) 3 C ) 5 D ) 1 E ) 2
6. В сосуде емкостью V при давлении p и температуре T находится идеальный газ . Число молекул газа можно вычислитьпо формуле
A ) 



7. На рисунке показаны процессы изменения состояния идеального газа. График изобары
8. Чтобы при постоянном давлении газа его температура уменьшилась в 3 раза, объем газа нужно
A ) увеличить в 3 раза B ) увеличить в 6 раз C ) уменьшить в 3 раза D ) не изменять E ) уменьшить в 6 раз
9
A ) 350 К B ) 210 К C ) 280 К D ) 300 К E ) 140 К
10. На рисунке приведены графики. Назовите их (в порядке 1-2-3)
A ) 1- изохора, 2- изобара, 3- изотерма B ) 1- изохора, 2- изотерма, 3- изобара
C ) 1- изотерма, 2- изохора, 3- изобара D ) 1- изобара, 2- изотерма, 3- изохора
E ) 1- изотерма, 2- изобара, 3- изохора
Краткое описание документа:
Тесты по теме «Уравнение Менделеева-Клапейрона» составлены для учащихся 10 классов физико-математического профиля обучения. Тесты составлены в соответствии с требования государственного стандарта и требованиями к знаниям, умениям и навыкам, предъявляемым учащимся 10 классов.Будут полезны учащимся в качестве самостоятельной подготовки к сдаче итоговой аттестации за 11 класс. Рекомендуется использовать при кратковременной проверке на уроках при изучении темы «Уравнение Менделеева- Клапейровна», а также в качестве проверочной итоговой работы при изучении раздела «Термодинамика». Ко всем вопросам приведены правильные ответы, что поможет учителю быстро проверить выполненную работу.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 860 человек из 78 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 47 человек из 21 региона
Курс профессиональной переподготовки
Физика: теория и методика преподавания в образовательной организации
- Сейчас обучается 364 человека из 72 регионов
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 845 491 материал в базе
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 08.02.2013
- 2853
- 3
- 07.02.2013
- 8452
- 3
- 07.02.2013
- 1379
- 0
- 06.02.2013
- 16713
- 15
- 06.02.2013
- 2430
- 0
- 06.02.2013
- 10235
- 4
- 05.02.2013
- 1927
- 0
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 09.02.2013 18853
- DOCX 1.2 мбайт
- 73 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Макарова Елена Геннадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 7 лет и 5 месяцев
- Подписчики: 0
- Всего просмотров: 173194
- Всего материалов: 69
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
Путин объявил 2022-2031 годы Десятилетием науки и технологий
Время чтения: 1 минута
Роспотребнадзор сообщил об опасности размещения вышек сотовой связи на территории школ
Время чтения: 1 минута
В России выросло число детей с ОВЗ, поступающих в колледжи
Время чтения: 1 минута
Минобрнауки отменило плановые и внеплановые проверки вузов в 2022 году
Время чтения: 1 минута
Инфофорум о буллинге в школе: итоги и ключевые идеи
Время чтения: 6 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
💥 Видео
Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Уравнение состояния идеального газаСкачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

29. Адиабатический процесс. Уравнение ПуассонаСкачать

Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Урок 146. Основное уравнение МКТ идеального газа - 2Скачать

Физика 10 Идеальный газ Основное уравнение МКТ идеального газа Решение задачСкачать

Уравнение состояния идеального газаСкачать

идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать

Идеальный газ в молекулярно-кинетической теории | Физика 10 класс #28 | ИнфоурокСкачать

Задачи на уравнение Менделеева-Клапейрона. Ч.1. Краткая теория + решение задачиСкачать

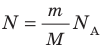
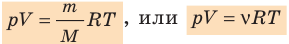
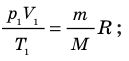
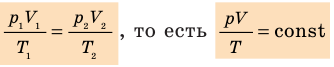
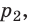
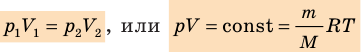

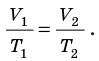
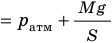
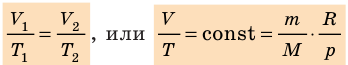
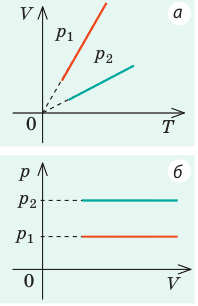

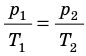
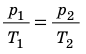
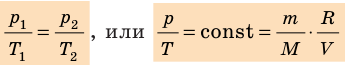

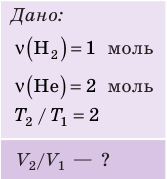
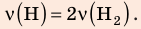

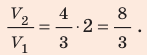
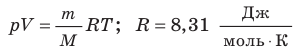 — универсальная газовая постоянная.
— универсальная газовая постоянная.