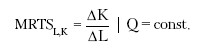Уравнение производственной функции и отдача от масштаба

ИЗОКВАНТА – кривая, демонстрирующая различные варианты комбинаций факторов производства, которые могут быть использованы для выпуска данного объема продукта. Изокванты иначе называют кривыми равных продуктов, или линиями равного выпуска.

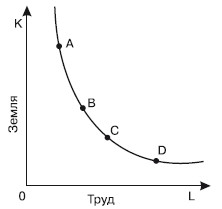
Наклон изокванты выражает зависимость одного фактора от другого в производственном процессе. При этом увеличение одного фактора и уменьшение другого не вызывают изменений в объеме выпускаемой продукции. Данная зависимость изображена на рис. 21.1.

Положительный наклон изокванты означает, что увеличение применения одного фактора потребует увеличения применения другого фактора, чтобы не сократить выпуск продукции. Отрицательный наклон изокванты показывает, что сокращение одного фактора (при определенном объеме производства) всегда будет вызывать увеличение другого фактора.

Изокванты выпуклы в направлении начала координат, поскольку хотя факторы могут быть заменяемы один другим, однако они не являются абсолютными заменителями.

Кривизна изокванты иллюстрирует эластичность замещения факторов при выпуске заданного объема продукта и отражает то, насколько легко один фактор может быть заменен другим. В том случае, когда изокванта похожа на прямой угол, вероятность замещения одного фактора другим крайне невелика. Если же изокванта имеет вид прямой линии с наклоном вниз, то вероятность замены одного фактора другим значительна.

Изокванты схожи с кривыми безразличия с той лишь разницей, что кривые безразличия выражают положение в сфере потребления, а изокванты – в сфере производства. Другими словами, кривые безразличия характеризуют замену одного блага другим (MRS), а изокванты – замену одного фактора другим (MRTS).

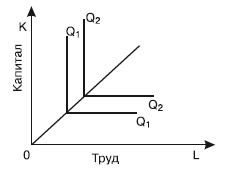
Чем дальше от начала координат расположена изокванта, тем больший объем выпуска она представляет. Крутизна наклона изокванты выражает предельную норму технического замещения (MRTS), которая измеряется соотношением изменения объема выпуска продукции. Предельная норма технического замещения трудом капитала (MRTS_LK) определяется величиной капитала, которую может заменить каждая единица труда, не вызывая изменения объема выпуска продукции. Предельная норма технического замещения в любой точке изокванты равна наклону касательной в этой точке, умноженному на -1:

Изокванты могут иметь различную конфигурацию: линейную, жесткой дополняемости, непрерывной замещаемости, ломаной изокванты. Здесь выделим две первые.

Линейная изокванта – изокванта, выражающая совершенную замещаемость факторов производства (MRTS_LK = const) (рис. 21.2).

Рис. 21.2. Линейная изокванта

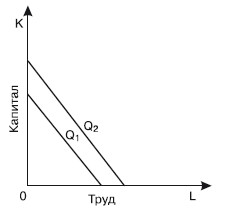
Жесткая дополняемость факторов производства представляет такую ситуацию, при которой труд и капитал сочетаются в единственно возможном соотношении, когда предельная норма технического замещения равна нулю (MRTS_LK = 0), так называемая изокванта леонтьевского типа (рис. 21.3).

Рис. 21.3. Жесткая изокванта

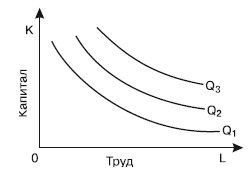
Карта изоквант представляет собой набор изоквант, каждая из которых иллюстрирует максимально допустимый объем производства продукции при любом данном наборе факторов производства. Карта изоквант является альтернативным способом изображения производственной функции.

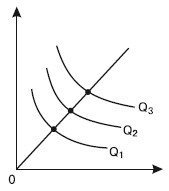
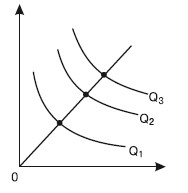
Смысл карты изоквант аналогичен смыслу карты кривых безразличия для потребителей. Карта изоквант схожа с контурной картой горы: все большие высоты показаны посредством кривых (рис. 21.4).

Карта изоквант может быть использована для того, чтобы показать возможности выбора среди множества вариантов организации производства в рамках короткого периода, когда, например, капитал является постоянным фактором, а труд – переменным фактором.

Рис. 21.4. Карта изоквант

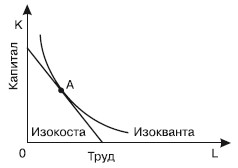
ИЗОКОСТА – линия, демонстрирующая комбинации факторов производства, которые можно купить за одинаковую общую сумму денег. Изокосту иначе называют линией равных издержек. Изокосты являются параллельными прямыми, поскольку допускается, что фирма может приобрести любое желаемое количество факторов производства по неизменным ценам. Наклон изокосты выражает относительные цены факторов производства (рис. 21.5). На рис. 21.5 каждая точка на линии изокосты характеризуется одними и теми же общими издержками. Эти линии прямые, поскольку факторные цены имеют отрицательный наклон и параллельны.

Рис. 21.5. Изокоста и изокванта

Совместив изокванты и изокосты, можно определить оптимальную позицию фирмы. Точка, в которой изокванта касается (но не пересекает) изокосты, означает наиболее дешевую по стоимости комбинацию факторов, необходимых для выпуска определенного объема продукта (рис. 21.5). На рис. 21.5 показан метод определения точки, в которой минимизируются издержки производства заданного объема производства продукта. Эта точка расположена на самой нижней изокосте, где изокванта соприкасается с ней.

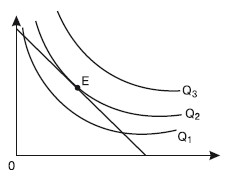
РАВНОВЕСИЕ ПРОИЗВОДИТЕЛЯ – состояние производства, при котором использование факторов производства позволяет получить максимальный объем продукции, т. е. когда изокванта занимает самую отдаленную от начала координат точку. Чтобы определить равновесие производителя, необходимо совместить карты изоквант с картой изокост. Максимальный объем выпуска будет в точке касания изокванты с изокостой (рис. 21.6).

Рис. 21.6. Равновесие производителя

Из рис. 21.6 видно, что изокванта, расположенная ближе к началу координат, дает меньшее количество производимой продукции (изокванта 1). Изокванты, расположенные выше и правее изокванты 2, вызовут изменение большего объема факторов производства, нежели позволяет бюджетное ограничение производителя.

Таким образом, точка касания изокванты и изокосты (на рис. 21.6 точка Е) является оптимальной, поскольку в этом случае производитель получает максимальный результат.

ОТДАЧА ОТ МАСШТАБА выражает реакцию объема производства продукции на пропорциональное изменение количества всех факторов производства.

Различают три положения отдачи от масштаба.

Возрастающая отдача от масштаба – положение, при котором пропорциональное увеличение всех факторов произволства приводит ко все большему увеличению объема выпуска продукта (рис. 21.7). Предположим, что все факторы производства увеличились в два раза, а объем выпуска продукта увеличился в три раза. Возрастающая отдача от масштаба обусловлена двумя основными причинами. Во-первых, повышением производительности факторов вследствие специализации и разделения труда при росте масштаба производства. Во-вторых, увеличение масштаба производства зачастую не требует пропорционального увеличения всех факторов производства. Например, увеличение вдвое производства цилиндрического оборудования (такого, как трубы) потребует увеличения металла меньше чем вдвое.

Постоянная отдача от масштаба – это изменение количества всех факторов производства, которое вызывает пропорциональное изменение объема выпуска продукта. Так, вдвое большее количество факторов ровно вдвое увеличивает объем выпуска продукта (рис. 21.8).

Убывающая отдача от масштаба – это ситуация, при которой сбалансированный рост объема всех факторов производства приводит ко все меньшему росту объема выпуска продукта. Иначе говоря, объем выпускаемой продукции увеличивается в меньшей степени, чем затраты факторов производства (рис. 21.9). Например, все факторы производства увеличились в три раза, а объем производства продукции – только в два раза.

Рис. 21.7. Возрастающая отдача от масштаба

Рис. 21.8. Постоянная отдача от масштаба

Рис. 21.9. Убывающая отдача от масштаба

Таким образом, в производственном процессе имеют место возрастающая, постоянная и убывающая отдачи от масштаба производства, когда пропорциональное увеличение количества всех факторов приводит к увеличившемуся, постоянному или убывающему приросту объема выпуска продукта.

Западные экономисты считают, что в настоящее время в большинстве видов производственной деятельности достигается постоянная отдача от масштаба. Во многих отраслях экономики возрастающая отдача от масштаба потенциально значима, однако с некоторого момента она может смениться убывающей отдачей, если не будет преодолен процесс увеличения числа гигантских фирм, что затрудняет управление и контроль, несмотря на то что технология производства стимулирует создание таких фирм.

Видео:Концепция отдачи от масштаба. Вывод издержек в долгосрочном периодеСкачать

Отдача от масштаба: понятие, ее увеличение и уменьшение

Отдача от масштаба показывает нам, как изменяется производство в ответ на увеличение всех вводимых ресурсов в долгосрочной перспективе. Отрасль может демонстрировать постоянную отдачу от масштаба, увеличивая отдачу от масштаба или уменьшая отдачу от масштаба.

Изучение того, растет ли эффективность с увеличением всех факторов производства, важно как для бизнеса, так и для политиков.

Оно дает возможность предприятиям определить оптимальный уровень производства и позволяет директивным органам определить, будет ли отрасль состоять из большого числа мелких производителей или из небольшого числа крупных производителей.

Закон убывающей отдачи говорит нам, что происходит, когда один параметр увеличивается, а другие остаются прежними.

Такая отдача наиболее актуальна в краткосрочном периоде, то есть во временном масштабе, в котором по крайней мере один фактор производства является постоянным.

В долгосрочной перспективе все факторы производства могут быть изменены, и именно тогда отдача от масштаба становится актуальной.

Существует три возможности для общей производственной функции, когда все вводимые ресурсы увеличиваются: а) увеличиваются с возрастающей скоростью, б) увеличиваются с фиксированной скоростью или в) увеличиваются с убывающей скоростью.

Эти три возможности приводят к трем формам отдачи от масштаба.

Прежде чем мы определим каждый тип, давайте рассмотрим производственную функцию Кобба-Дугласа:

Q = A × L a × K b , где

Q — общий продукт,

L и K — соответственно единицы труда и капитала, а

A, a и b — константы.

Видео:6.2.1. Производственная функцияСкачать

Постоянная отдача от масштаба

Постоянная отдача от масштаба означает, что общий продукт изменяется пропорционально увеличению всех вводимых ресурсов.

Процентное увеличение общего продукта при постоянной отдаче от масштаба совпадает с процентным увеличением всех вводимых ресурсов.

Если сумма a и b в производственной функции Кобба-Дугласа равна 1, то она представляет собой постоянную отдачу от масштабу.

Видео:Концепция отдачи от масштабаСкачать

Примеры

Постоянная отдача от масштаба преобладает в очень малых предприятиях. Например, давайте рассмотрим автомойку, в которой мойка одной автомашины занимает 30 минут.

Если есть одно моечное пространство (гидравлический домкрат) и два рабочих, работающих в две 8-часовые смены, общий продукт составит 32.

Если есть два моечных пространства и четыре рабочих, то есть когда входы удваиваются, общее количество моек может увеличиться до 64 (=4 × 8 × 60/30) и так далее.

Видео:7.2.3. Связь эффекта масштаба с производственными функциямиСкачать

Увеличение отдачи от масштаба

В отраслях, где наблюдается увеличение отдачи от масштаба, увеличение общего объема вводимых ресурсов на 1 % приведет к увеличению общего объема продукции более чем на 1 %.

Другими словами, общий объем продукции увеличивается со скоростью, превышающей скорость увеличения всех вводимых ресурсов. Увеличение отдачи от масштаба также называют эффектом масштаба.

Не противоречит ли это закону убывающей отдачи? Нет, не противоречит.

Так происходит не потому, что закон убывающей отдачи применим только в краткосрочной перспективе для изменения только одного входного сигнала, а потому, что отдача от масштаба определяет изменение общего продукта в ответ на изменения всех входных данных.

Причины увеличения отдачи от масштаба включают специализацию труда, синергию и так далее. Сумма a и b в производственной функции Кобба-Дугласа выше 1 в случае увеличения отдачи от масштаба.

Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Примеры

Отрасли промышленности, которые демонстрируют растущую отдачу от масштаба, как правило, имеют небольшое число крупных фирм.

Поскольку производство на высоком уровне имеет свои преимущества, крупные компании имеют значительное преимущество по сравнению с мелкими фирмами.

Производители самолетов, крупные компании экспресс-доставки, телекоммуникационные компании и так далее демонстрируют возрастающую отдачу от масштаба.

Видео:Производная функции. 10 класс.Скачать

Уменьшение отдачи от масштаба

В случае уменьшения отдачи от масштаба общий продукт увеличивается со скоростью, меньшей, чем скорость увеличения вводимых ресурсов.

Другими словами, дополнительные инвестиции постепенно порождают все меньше и меньше дополнительного производства.

Если сумма a и b в производственной функции Кобба-Дугласа меньше 1, то это означает уменьшение отдачи от масштаба. Снижение отдачи от масштаба также называют отрицательным эффектом масштаба.

Видео:Граница производственных возможностей. Оптимум по ПаретоСкачать

Примеры

Примерами отраслей, которые демонстрируют снижение отдачи от масштаба, являются компании, занимающиеся разведкой природных ресурсов (поскольку добыча становится все более трудной по мере того, как добываются более легкие низко висящие полезные ископаемые), компании, где сложность приводит к более высокому риску отказа, такие как распределение электроэнергии и тому подобные.

Эффект масштаба может быть графически с использованием изоквант.

Видео:Эффект масштаба - просто о сложномСкачать

Отдача от масштаба производства (эффект масштаба): постоянная, возрастающая и убывающая

12.11.2021 No Comments Posted in

Что такое “отдача от масштаба производства” или “эффект масштаба”

Фирмы, испытывающие эффект масштаба производства, замечают, что изменение их средних общих издержек в долгосрочном периоде очень сильно зависит от количества выпускаемой продукции.

Таким образом, отдача от масштаба (эффект масштаба) выражает реакцию объема производства продукции на пропорциональное изменение всех факторов производства.

Создавайте презентации, запоминающиеся публикации, фотоколлажи, инфографику, открытки, плакаты, визитки, оформляйте документы в визуальном редакторе Canva. После регистрации по ссылке каждый подписчик получит 30-дневный бесплатный пробный период Canva Pro.

Видео:Экономика. Альтернативные издержки. Построение КПВ, уравнение КПВ, сложение линейных КПВСкачать

Какие факторы влияют на отдачу от масштаба производства

Чаще всего эффект масштаба возникает в случае изменения технологии производства. Например, в результате развития специализации отдельные работники могут концентрироваться на выполнении специализированных задач, при этом они получают больше опыта и знаний в своей области, что позволяет им эффективнее выполнять свои задачи.

Кроме того, на отдачу от масштаба производства влияют высокие издержки, которые возникают у фирмы в момент вступления в отрасль. В таких отраслях, как автомобилестроение или нефтепереработка, первоначальные издержки очень высокие. Производство даже небольшого количества продукции требует вложения огромной суммы денег, необходимой для строительства предприятий и закупки оборудования. Эффект масштаба в данном случае имеет решающее значение на монопольном и олигопольном рынках.

Отрицательный эффект масштаба зачастую возникает из-за проблем коммуникации и координации: с ростом размеров предприятия все труднее и дороже становится осуществлять взаимосвязи и организовывать деятельность компании.

Видео:14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

Возрастающая, убывающая и постоянная отдача от масштаба производства

Различают 3 положения отдачи от масштаба:

• возрастающая (положительный эффект масштаба)— положение, при котором пропорциональное увеличение всех факторов производства приводит ко все большему увеличению объемов выпуска продукции. Зачастую, рост масштаба производства не требует пропорционального увеличения всех факторов производства. Например, для увеличения производства минеральных удобрений в 2 раза понадобится увеличить количество используемой селитры меньше, чем вдвое.
• убывающая (отрицательный эффект масштаба) — положение, при котором рост объема всех факторов производства приводит ко все меньшему росту объема выпуска продукции. То есть, объем производства увеличивается в меньшей степени, чем затраты факторов производства. Например, увеличили количество работников в 3 раза и закупили оборудование, а объем выпуска продукции увеличился только в 2 раза.
• постоянная (нейтральный эффект масштаба) — положение, при котором изменение количества всех факторов производства вызывает пропорциональное изменение объема выпуска продукции. Например, увеличили количество оборудования в 2 раза, и в 2 раза увеличился объем производства.

Видео:Производственная функция Задачи с решениями и без.Скачать

Как определить тип отдачи от масштаба производства

Если выбран технически эффективный способ производства, то увеличение выпуска возможно за счет пропорционального увеличения использования всех производственных ресурсов. Это и есть изменение масштаба производства.

Пусть первоначальное соотношение между выпуском и применяемыми ресурсами описывается производственной функцией:

Если мы увеличим объемы применяемых ресурсов (масштаб производства) в k раз, то новый объем выпуска, очевидно, составит:

Если в результате данного увеличения ресурсов выпуск увеличится также в k раз (Q₁=kQ₀), то наблюдается постоянная отдача от масштаба:

Если выпуск увеличится менее, чем в k раз (Q₁ Убывающая отдача от масштаба производства (отрицательный эффект масштаба)

Если выпуск увеличится более, чем в k раз (Q₁>kQ₀), то имеет место возрастающая отдача от масштаба:

Видео:4.3 Закон убывающей предельной производительностиСкачать

Степень однородности производственной функции

Введем еще одну характеристику производственной функции – однородность.

Производственная функция называется однородной, если при увеличении количества всех производственных ресурсов в k раз выпуск увеличивается в k t раз, так что:

Показатель t характеризует степень однородности функции. Если же равенство Q₁(kK,kL) = K t Q₀(К,L) для данной производственной функции не выполняется, то такая производственная функция называется неоднородной.

Степень однородности может использоваться для характеристики типа отдачи от масштаба:

• Если t = 1, то отдача от масштаба постоянна, а производственная функция в этом случае обычно называется линейно-однородной.
• Если t 1 — возрастающая отдача от масштаба.

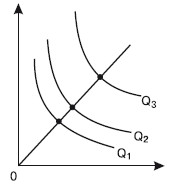
Для однородной производственной функции отдача от масштаба может быть представлена графически. Показателем отдачи может служить расстояние вдоль луча, проведенного из начала координат, между изоквантами, представляющими кратные Q объемы выпуска – Q, 2Q, 3Q и т.д.

В случае неоднородности производственной функции оценка отдачи от масштаба и ее графическое отображение могут представить значительные трудности.

Лучи, проведенные из начала координат на графиках, называют линиями роста. Они характеризуют технически возможные пути расширения производства, перехода с более низкой на более высокую изокванту. Среди возможных линий роста представляют интерес изоклинали, вдоль которых предельно технического замещения ресурсов при любом объеме выпуска постоянна. Для однородной производственной функции изоклиналь представляется лучом, проведенным из начала координат, вдоль которого предельная норма технического замещения и соотношение К/L имеют одно и то же значение.

Видео:Производственная функция | Эффективное комбинирование факторов производстваСкачать

Отдача от масштаба: примеры

Постоянная отдача от масштаба наблюдается в тех производствах, где ресурсы однородны (в техническом смысле) и их количество можно изменять пропорционально. В таких производствах увеличение выпуска может быть достигнуто путем кратного увеличения объема применения всех производственных ресурсов.

Убывающая отдача, как правило, связана с ограниченными возможностями управления крупным производством. Концентрация управления (на неизменной технической базе) сверх определенного предела ведет к нарушению координации потоков ресурсы—выпуск.

Во многих случаях характер отдачи от масштаба изменяется при достижении определенных пределов выпуска. До определенных пределов рост производства может сопровождаться постоянной и даже возрастающей отдачей от масштаба, которая затем сменяется убывающей.

Например, в некоторых производствах возрастающая отдача является следствием геометрического закона соответствия поверхностей и объемов. Так, поверхности шаров растут как квадраты, а их объемы — как кубы радиусов. Поскольку производительность установок, имеющих подобную форму, зависит от их объемов, а расход металла на их сооружение — от площади поверхности, рост производительности таких установок опережает рост их металлоемкости. Однако увеличение объемов ведет и к повышению давления внутри установки, что требует увеличения толщины ее стенок, а это значит, что расход металла на ее сооружение увеличивается в большей степени, чем растет ее поверхность. В итоге возрастающая отдача от масштаба сменяется постоянной или убывающей.

Другой пример. Расход металла на сооружение трубопровода прямо пропорционален его окружности (при данной длине), тогда как его пропускная способность зависит от площади сечения (при данной скорости потока жидкости или газа). Окружность трубопровода равна 2πR, а площадь сечения πR 2 , где R — длина радиуса. Значит, при увеличении радиуса вдвое окружность трубопровода удвоится, тогда как площадь сечения увеличится в 4 раза (4 πR 2 ). В результате при удвоении расхода металла на сооружение трубопровода его производительность учетверится. Но при этом будет возрастать и давление внутри трубопровода, что потребует увеличения толщины труб и, значит, расхода металла. Таким образом, и в этом случае возрастающая отдача сменится при достижении определенного уровня постоянной, а затем и убывающей.

Заключение

Таким образом, в производственном процессе встречается возрастающая, убывающая и постоянная отдача от масштаба производства, когда пропорциональное увеличение количества всех факторов производства приводит к увеличивающемуся, убывающему или постоянному приросту объема выпуска продукции.

В настоящее время в большинстве видов производственной деятельности наблюдается постоянная отдача от масштаба производства.

💥 Видео

"Производство" Интенсив к региону УмбрияСкачать

4. Вычисление производных примеры. Самое начало.Скачать

Построение производственной функции Кобба-ДугласаСкачать

КПВ для возрастающих, убывающих и постоянных альтернативных издержек | МакроэкономикаСкачать

11. Производная неявной функции примерыСкачать

Олимпиадная Экономика 2020. Кривая торговых возможностей (КТВ), построение.Скачать

4.2 Производственная деятельность фирмыСкачать