Уравнение проходящего через середину отрезка

Видео:Координаты середины отрезкаСкачать

Уравнение прямой проходящей через середину отрезка параллельно прямой

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Составить уравнение прямой проходящей через середину отрезка АВ, параллельно прямой y = 2x + 5 , если А (2, — 1) и В (0, 7)?

Геометрия | 5 — 9 классы

Составить уравнение прямой проходящей через середину отрезка АВ, параллельно прямой y = 2x + 5 , если А (2, — 1) и В (0, 7).

Прямая — график линейной функции, то есть y = kx + b.

Так как искомаяпрямая проходит параллельно прямой y = 2x + 5, то их угловые коэфициенты равны.

Середина отрезка AB — точка O.

Найдем ее координаты :

x = (xA + xB) / 2 = (2 + 0) / 2 = 1

y = (yA + yB) / 2 = ( — 1 + 7) / 2 = 3

Найдем b, для этого подставим координаты точки O :

значит искомое уравнение прямой — y = 2x + 1.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Отрезки АВ и CD пересекаются в их общей середине?

Отрезки АВ и CD пересекаются в их общей середине.

Докажите, что прямые АС и BD параллельны.

Видео:Построение середины отрезкаСкачать

) Вершины В и С треугольника АВС лежат в плоскости beta ?

) Вершины В и С треугольника АВС лежат в плоскости beta .

Вершина А ей не принадлежит.

Докажите, что прямая, проходящая через середины отрезков АВ и АС, параллельна плоскости beta .

Видео:Координаты середины отрезка. Уравнение средней линии или диагонали. Урок 4. Геометрия 8 класс.Скачать

1) Вершины В и С треугольника АВС лежат в плоскости ?

1) Вершины В и С треугольника АВС лежат в плоскости .

Вершина А ей не принадлежит.

Докажите, что прямая, проходящая через середины отрезков АВ и АС, параллельна плоскости .

Видео:Уравнения стороны треугольника и медианыСкачать

Концы отрезка АВ лежат на параллельных прямых a и b?

Концы отрезка АВ лежат на параллельных прямых a и b.

Прямая, проходящая через середину О этого отрезка , пересекает прямые a и b в точках С и D.

Докажите что СО = ОD.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Отрезки АВ и СD пересекаются в их общей середине?

Отрезки АВ и СD пересекаются в их общей середине.

Докажите, что прямые AC и BD параллельны.

Видео:№276. Через середину отрезка проведена прямая. Докажите, что концы отрезка равноудалены от этойСкачать

Отрезки АВ и CD пересекаются в точке О, являющейся их серединой?

Отрезки АВ и CD пересекаются в точке О, являющейся их серединой.

Докажите параллельность прямых АС и ВD.

Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Докажите, что середина отрезка прямой, заключенного между двумя параллельными прямыми, является серединой отрезков прямых, проходящих через эту точку и заключенных между теми же параллельными прямыми?

Докажите, что середина отрезка прямой, заключенного между двумя параллельными прямыми, является серединой отрезков прямых, проходящих через эту точку и заключенных между теми же параллельными прямыми.

Видео:Геометрия Задача- Ловушка Help Найти середину отрезка циркулемСкачать

Перпендикулярные отрезки KN и PM пересекаются в их общей середине?

Перпендикулярные отрезки KN и PM пересекаются в их общей середине.

Начертите прямую, проходящую через точку К, параллельную прямой, содержащей отрезок PM.

Видео:Координаты середины отрезка. Формула. Геометрия 9 класс.Скачать

⦁Отрезки АС и BD пересекаются в их общей середине точке О?

⦁Отрезки АС и BD пересекаются в их общей середине точке О.

Докажите, что прямые АВ и CD параллельны.

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Постройте прямую, проходящую через середину О отрезка АВ и перпендикулярную этому отрезку?

Постройте прямую, проходящую через середину О отрезка АВ и перпендикулярную этому отрезку.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Составить уравнение прямой проходящей через середину отрезка АВ, параллельно прямой y = 2x + 5 , если А (2, — 1) и В (0, 7)?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

С) т. К. у ромба перпендикулярные диагонали, а не у прямоугольника.

Периметр равен 4см * 2 + 15 + 14.

6. 68 дм / 4 стороны = 17 дм. 7. треугольник BCD является прямоугольным, в нем прямой угол DCB равен 90° градусов. В другом таком же треугольнике этот угол равен тоже 90°. Сумма углов треугольника равна 180° градусов. Прямой угол 90°, нужно ещё н..

272(2) = а * b = 38 м2 274(3, 4) = 3. = б * с = 17 м2 4. = а * с = 4, 8 м2.

Вот так, если что — то ещё, то пишите).

По теореме об отрезках хорд AM * BM = CM * DM. По условию AM = 3, CM = DM, так что 3BM = CM². BM = AB — AM = 15 — 3 = 12, так что 3 * 12 = CM². 36 = CM² CM = 6 DM = CM = 6 CD = CM + DM = 6 + 6 = 12 Ответ : CD = 12 см .

Прошу прощения, не ту формулу взял. Вот формула V = Число пи * r ^ 2 * h тогда 3. 1415 * 12. 5 * 12. 5 * 40 = 19634, 375 см ^ 3, отсюда примерно 19, 63 литра.

Схематически нарисуйте окружность и касательную AB. OA является радиусом = > OA = 2 см. Так как OA = AB, то AB = 2 см. Угол при вершине A = 90 градусов = > Треугольник прямоугольный. По теореме Пифагора находим OB : OB = корень из ( 2 ^ 2 + 2 ^ 2..

— 4sina — 7cos * ( — tga) + sina = — 3sina — 7cos * ( — tga).

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Уравнение прямой в отрезках: описание, примеры, решение задач

Продолжаем изучение раздела «Уравнение прямой на плоскости» и в этой статье разберем тему «Уравнение прямой в отрезках». Последовательно рассмотрим вид уравнения прямой в отрезках, построение прямой линии, которая задается этим уравнением, переход от общего уравнения прямой к уравнению прямой в отрезках. Все это будет сопровождаться примерами и разбором решения задач.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Уравнение прямой в отрезках – описание и примеры

Пусть на плоскости расположена прямоугольная система координат O x y .

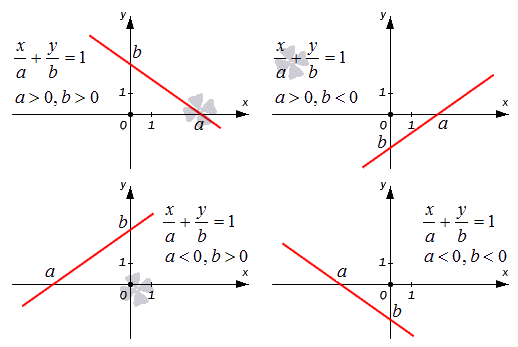
Прямая линия на плоскости в декартовой системе координат O x y задается уравнением вида x a + y b = 1 , где a и b – это некоторые действительные числа, отличные от нуля, величины которых равны длинам отрезков, отсекаемых прямой линией на осях O x и O y . Длины отрезков считаются от начала координат.

Как мы знаем, координаты любой из точек, принадлежащих прямой линии, заданной уравнением прямой, удовлетворяют уравнению этой прямой. Точки a , 0 и 0 , b принадлежат данной прямой линии, так как a a + 0 b = 1 ⇔ 1 ≡ 1 и 0 a + b b = 1 ⇔ 1 ≡ 1 . Точки a , 0 и b , 0 расположены на осях координат O x и O y и удалены от начала координат на a и b единиц. Направление, в котором нужно откладывать длину отрезка, определяется знаком, который стоит перед числами a и b . Знак « — » обозначает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.

Поясним все вышесказанное, расположив прямые относительно фиксированной декартовой системы координат O x y на схематическом чертеже. Уравнение прямой в отрезках x a + y b = 1 применяется для построения прямой линии в декартовой системе координат O x y . Для этого нам необходимо отметить на осях точки a , 0 и b , 0 , а затем соединить эти точки линией при помощи линейки.

На чертеже показаны случаи, когда числа a и b имеют различные знаки, и, следовательно, длины отрезков откладываются в разных направлениях координатных осей.

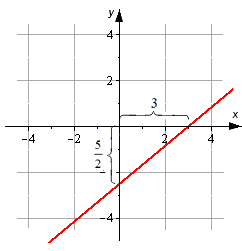
Прямая линия задана уравнением прямой в отрезках вида x 3 + y — 5 2 = 1 . Необходимо построить эту прямую на плоскости в декартовой системе координат O x y .

Решение

Используя уравнение прямой в отрезках, определим точки, через которые проходит прямая линия. Это 3 , 0 , 0 , — 5 2 . Отметим их и проведем линию.

Видео:Расстояние между двумя точками. Координаты середины отрезка.Скачать

Приведение общего уравнения прямой к уравнению прямой в отрезках

Переход от заданного уравнения прямой к уравнению прямой в отрезках облегчает нам решение различных задач. Имея полное общее уравнение прямой, мы можем получить уравнение прямой в отрезках.

Полное общее уравнение прямой линии на плоскости имеет вид A x + B y + C = 0 , где А , В и C не равны нулю. Мы переносим число C в правую часть равенства, делим обе части полученного равенства на – С . При этом, коэффициенты при x и y мы отправляем в знаменатели:

A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1

Для осуществления последнего перехода мы воспользовались равенством p q = 1 q p , p ≠ 0 , q ≠ 0 .

В результате, мы осуществили переход от общего уравнения прямой A x + B y + C = 0 к уравнению прямой в отрезках x a + y b = 1 , где a = — C A , b = — C B .

Разберем следующий пример.

Осуществим переход к уравнению прямой в отрезках, имея общее уравнение прямой x — 7 y + 1 2 = 0 .

Решение

Переносим одну вторую в правую часть равенства x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .

Делим обе части равенства на — 1 2 : x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .

Преобразуем полученное равенство к нужному виду: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .

Мы получили уравнение прямой в отрезках.

Ответ: x — 1 2 + y 1 14 = 1

В тех случаях, когда прямая линия задана каноническим или параметрическим уравнением прямой на плоскости, то сначала мы переходим к общему уравнению прямой, а затем уже к уравнению прямой в отрезках.

Перейти от уравнения прямой в отрезках и общему уравнению прямой осуществляется просто: мы переносим единицу из правой части уравнения прямой в отрезках вида x a + y b = 1 в левую часть с противоположным знаком, выделяем коэффициенты перед неизвестными x и y .

x a + y b = 1 ⇔ x a + y b — 1 = 0 ⇔ 1 a · x + 1 b · y — 1 = 0

Получаем общее уравнение прямой, от которого можно перейти к любому другому виду уравнения прямой на плоскости. Процесс перехода мы подробно разобрали в теме «Приведение общего уравнения прямой к другим видам уравнения прямой».

Уравнение прямой в отрезках имеет вид x 2 3 + y — 12 = 1 . Необходимо написать общее уравнение прямой на плоскости.

Решение

Действует по заранее описанному алгоритму:

x 2 3 + y — 12 = 1 ⇔ 1 2 3 · x + 1 — 12 · y — 1 = 0 ⇔ ⇔ 3 2 · x — 1 12 · y — 1 = 0

Ответ: 3 2 · x — 1 12 · y — 1 = 0

Видео:Длина отрезкаСкачать

Прямая на плоскости. Примеры решений

Решение проводим с помощью калькулятора.
Даны координаты треугольника: A(2,1), B(1,-2), C(-1,0).
1) Координаты векторов
Координаты векторов находим по формуле:
X = x_j — x_i; Y = y_j — y_i
здесь X,Y координаты вектора; x_i, y_i — координаты точки А_i; x_j, y_j — координаты точки А_j
Например, для вектора AB
X = x₂ — x₁; Y = y₂ — y₁
X = 1-2 = -1; Y = -2-1 = -3
AB(-1;-3)
AC(-3;-1)
BC(-2;2)
2) Модули векторов
Длина вектора a(X;Y) выражается через его координаты формулой:




3) Угол между прямыми
Угол между векторами a₁(X₁;Y₁), a₂(X₂;Y₂) можно найти по формуле:

где a₁a₂ = X₁X₂ + Y₁Y₂
Найдем угол между сторонами AB и AC

γ = arccos(0.6) = 53.13 0
4) Проекция вектора
Проекцию вектора b на вектор a можно найти по формуле:

Найдем проекцию вектора AB на вектор AC

5) Площадь треугольника
Пусть точки A₁(x₁; y₁), A₂(x₂; y₂), A₃(x₃; y₃) — вершины треугольника, тогда его площадь выражается формулой:

В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Решение. Принимая A за первую вершину, находим:

Пример. Даны координаты вершин треугольника АВС: А(–3; –1), В(4; 6), С(8; –2).
Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

Задание. Даны координаты вершин треугольника ABC: A(7;4), B(-9;-8), C(-2;16). Требуется:

1. составить уравнение медианы, проведенной из вершины B, и вычислить ее длину.
2. составить уравнение высоты, проведенной из вершины A, и вычислить ее длину.
3. найти косинус внутреннего угла B треугольника ABC.

Пример №3. Даны вершины A(1;1), B(7;4), C(4;5) треугольника. Найти: 1) длину стороны AB ; 2) внутренний угол A в радианах с точностью до 0,001. Сделать чертеж.
Скачать

Пример №4. Даны вершины A(1;1), B(7;4), C(4;5) треугольника. Найти: 1) уравнение высоты, проведенной через вершину C ; 2) уравнение медианы, проведенной через вершину C ; 3) точку пересечения высот треугольника; 4) длину высоты, опущенной из вершины C. Сделать чертеж.
Скачать

Пример №5. Даны вершины треугольника ABC: A(-5;0), B(7;-9), C(11;13). Определите: 1) длину стороны AB ; 2) уравнение сторон AB и AC и их угловые коэффициенты; 3) площадь треугольника.

Задание. Найти острый угол между прямыми x + y -5 = 0 и x + 4y — 8 = 0 .
Рекомендации к решению. Задача решается посредством сервиса Угол между двумя прямыми.
Ответ: 30.96 o

Пример №1. Даны координаты точек А1(1;0;2), A2(2;1;1), А3(-1;2;0), A4(-2;-1;-1). Найти длину ребра А1А2. Составить уравнение ребра А1А4 и грани А1А2А3. Составить уравнение высоты опущенной из точки А4 на плоскость А1А2А3. Найти площадь треугольника А1A2A3. Найти объем треугольной пирамиды А1A2А3A4.

Задание. По координатам вершин пирамиды А1,А2,А3,А4 найти: 1) длины ребер А1А2 и А1А3; 2) угол между ребрами А1А2 и А1А3; 3) площадь грани А1А2А3;4) объем пирамиды А1А2А3А4
A₁(3;5;4,0,0), A₂(8;7;4,0,0), A₃(5;10;4,0,0), A₄(4;7;9,0,0):Пример №10

Пример. В декартовой прямоугольной системе координат даны вершины пирамиды A, B, C, D. Найдите длину ребра AB, косинус угла между векторами, уравнение ребра, уравнение грани, уравнение высоты.
Решение

Пример. Даны вершины треугольника А(1, –1, -3), В(2, 0, -10), С(3, 0, -2).
а) Найти уравнение биссектрисы и высоты данного треугольника, проведенных из вершины A .
б) Найти уравнения всех его медиан и координаты точки их пересечения.
см. также Как найти периметр треугольника

Видео:Построение середины отрезкаСкачать

Составьте уравнение серединного перпендикуляра отрезка АВ, если А (3; 2) и В (-2; 1).

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Ваш ответ

Видео:Нахождение координаты середины отрезка.Скачать

решение вопроса

Видео:8 класс. Геометрия. Нахождение координат середины отрезка. 10.04.2020Скачать

Похожие вопросы

• Все категории
• экономические 43,293
• гуманитарные 33,622
• юридические 17,900
• школьный раздел 607,176
• разное 16,830

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Составить уравнение прямой проходящей через середину отрезка АВ, параллельно прямой y = 2x + 5 , если А (2, — 1) и В (0, 7)?

Геометрия | 5 — 9 классы

Составить уравнение прямой проходящей через середину отрезка АВ, параллельно прямой y = 2x + 5 , если А (2, — 1) и В (0, 7).

Прямая — график линейной функции, то есть y = kx + b.

Так как искомаяпрямая проходит параллельно прямой y = 2x + 5, то их угловые коэфициенты равны.

Середина отрезка AB — точка O.

Найдем ее координаты :

x = (xA + xB) / 2 = (2 + 0) / 2 = 1

y = (yA + yB) / 2 = ( — 1 + 7) / 2 = 3

Найдем b, для этого подставим координаты точки O :

значит искомое уравнение прямой — y = 2x + 1.

Отрезки АВ и CD пересекаются в их общей середине?

Отрезки АВ и CD пересекаются в их общей середине.

Докажите, что прямые АС и BD параллельны.

) Вершины В и С треугольника АВС лежат в плоскости beta ?

) Вершины В и С треугольника АВС лежат в плоскости beta .

Вершина А ей не принадлежит.

Докажите, что прямая, проходящая через середины отрезков АВ и АС, параллельна плоскости beta .

1) Вершины В и С треугольника АВС лежат в плоскости ?

1) Вершины В и С треугольника АВС лежат в плоскости .

Вершина А ей не принадлежит.

Докажите, что прямая, проходящая через середины отрезков АВ и АС, параллельна плоскости .

Концы отрезка АВ лежат на параллельных прямых a и b?

Концы отрезка АВ лежат на параллельных прямых a и b.

Прямая, проходящая через середину О этого отрезка , пересекает прямые a и b в точках С и D.

Докажите что СО = ОD.

Отрезки АВ и СD пересекаются в их общей середине?

Отрезки АВ и СD пересекаются в их общей середине.

Докажите, что прямые AC и BD параллельны.

Отрезки АВ и CD пересекаются в точке О, являющейся их серединой?

Отрезки АВ и CD пересекаются в точке О, являющейся их серединой.

Докажите параллельность прямых АС и ВD.

Докажите, что середина отрезка прямой, заключенного между двумя параллельными прямыми, является серединой отрезков прямых, проходящих через эту точку и заключенных между теми же параллельными прямыми?

Докажите, что середина отрезка прямой, заключенного между двумя параллельными прямыми, является серединой отрезков прямых, проходящих через эту точку и заключенных между теми же параллельными прямыми.

Перпендикулярные отрезки KN и PM пересекаются в их общей середине?

Перпендикулярные отрезки KN и PM пересекаются в их общей середине.

Начертите прямую, проходящую через точку К, параллельную прямой, содержащей отрезок PM.

⦁Отрезки АС и BD пересекаются в их общей середине точке О?

⦁Отрезки АС и BD пересекаются в их общей середине точке О.

Докажите, что прямые АВ и CD параллельны.

Постройте прямую, проходящую через середину О отрезка АВ и перпендикулярную этому отрезку?

Постройте прямую, проходящую через середину О отрезка АВ и перпендикулярную этому отрезку.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Составить уравнение прямой проходящей через середину отрезка АВ, параллельно прямой y = 2x + 5 , если А (2, — 1) и В (0, 7)?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.