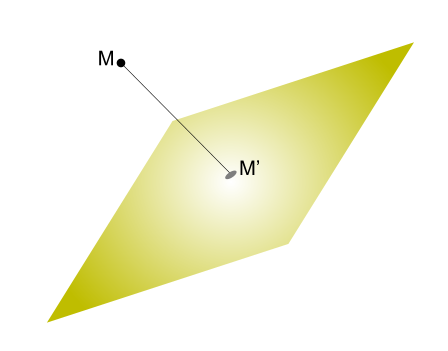
С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
- Предупреждение
- Проекция точки на плоскость − теория, примеры и решения
- Проекция точки на плоскость онлайн
- Как найти проекцию точки на плоскость: методика определения и пример решения задачи
- Уравнение для описания плоскости
- Понятие о проекции точки и ее вычисление
- Вычисление расстояния от плоскости до точки
- Пример задачи
- 📹 Видео
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Проекция точки на плоскость, проекция прямой на плоскость. Параллельные прямые.Скачать

Проекция точки на плоскость − теория, примеры и решения
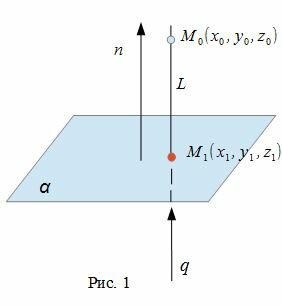
Для нахождения проекции точки M0 на плоскость α, необходимо:
- построить прямую L, проходящую через точку M0 и ортогональной плоскости α.
- найти пересечение данной плоскости α с прямой L(Рис.1).
 |
Общее уравнение плоскости имеет вид:
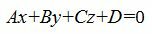 | (1) |
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
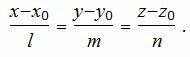 | (2) |
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональной плоскости (1) имеет следующий вид:
 | (3) |
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
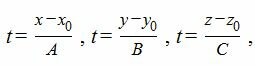 |
Выразим переменные x, y, z через рараметр t.
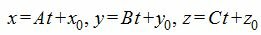 | (4) |
Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
| A(At+x0)+B(Bt+y0)+C(At+z0)+D=0, |
| A 2 t+Ax0+B 2 t+By0+C 2 t+Cz0+D=0, |
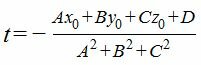 | (5) |
Подставляя значение параметра t в выражения (4), находим проекцию M1 точки M0 на плоскость (1).
Пример 1. Найти проекцию M1 точки M0(4, -3, 2) на плоскость
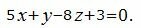 | (6) |
Нормальный вектор плоскости имеет вид:
Подставляя координаты точки M0 и нормального вектора плоскости в (5), получим:
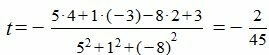 | (7) |
Из выражений (7) находим:
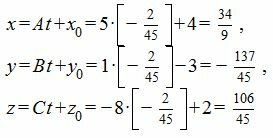 |
Проекцией точки M0(4, -3, 2) на плоскость (6) является точка:
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Проекция точки на плоскость онлайн
| Коэффициенты плоскости |
| Координаты точки разделенные хотя бы одним пробелом |
| Координаты проекции точки |
В данном материале мы рассмотрим решение задачи нахождения координат проекции точки на какую либо плоскость в пространстве.
Теории практически не будет и думаю для тех кто интересуется могут понять это все из ниже разобранного примера
Найти проекцию точки M(1,-3,2) на плоскость 2x+5y-3z-19=0
Проекция точки М на данную поверхность — есть точка пересечения с данной плоскостью прямой, проходящей через точку М перпендикулярно к данной плоскости.
Уравнение прямой, проходящей через точку M(1,-3,2) перпедикулярно к плоскости 2x+5y-3z-19=0 имеет вид
или в виде системы
Добавив сюда исходное уравнение плоскости получим полноценную систему линейных уравнений которая легко решается
В данном примере проекция точки имеет координаты (3,2,-1)
Видео:23. Точка пересечения прямой и плоскости / Проекция точки на плоскость / Проекция точки на прямуюСкачать

Как найти проекцию точки на плоскость: методика определения и пример решения задачи
При решении геометрических задач в пространстве часто возникает проблема определения расстояния между плоскостью и точкой. В некоторых случаях это необходимо для комплексного решения. Эту величину можно вычислить, если найти проекцию на плоскость точки. Рассмотрим этот вопрос подробнее в статье.
Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Уравнение для описания плоскости
Перед тем как перейти к рассмотрению вопроса касательно того, как найти проекцию точки на плоскость, следует познакомиться с видами уравнений, которые задают последнюю в трехмерном пространстве. Подробнее — ниже.

Уравнением общего вида, определяющим все точки, которые принадлежат данной плоскости, является следующее:
A*x + B*y + C*z + D = 0.
Первые три коэффициента — это координаты вектора, который называется направляющим для плоскости. Он совпадает с нормалью для нее, то есть является перпендикулярным. Этот вектор обозначают n¯(A; B; C). Свободный коэффициент D однозначно определяется из знания координат любой точки, принадлежащей плоскости.
Далее в статье будем использовать записанное уравнение. Оно требуется, чтобы найти проекцию точки на плоскость.
Видео:Прямая на плоскости. Проекция точки на прямуюСкачать

Понятие о проекции точки и ее вычисление
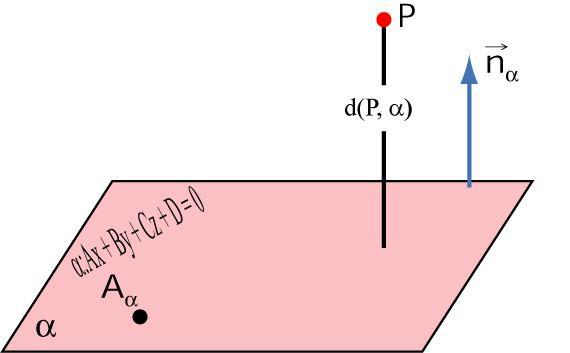
Предположим, что задана некоторая точка P(x1; y1; z1) и плоскость. Она определена уравнением в общем виде. Если провести перпендикулярную прямую из P к заданной плоскости, то очевидно, что она пересечет последнюю в одной определенной точке Q (x2; y2; z2). Q называется проекцией P на рассматриваемую плоскость. Длина отрезка PQ называется расстоянием от точки P до плоскости. Таким образом, сам PQ является перпендикулярным плоскости.
Как можно найти координаты проекции точки на плоскость? Сделать это не сложно. Для начала следует составить уравнение прямой, которая будет перпендикулярна плоскости. Ей будет принадлежать точка P. Поскольку вектор нормали n¯(A; B; C) этой прямой должен быть параллелен, то уравнение для нее в соответствующей форме запишется так:
(x; y; z) = (x1; y1; z1) + λ*(A; B; C).
Где λ — действительное число, которое принято называть параметром уравнения. Изменяя его, можно получить любую точку прямой.
После того как записано векторное уравнение для перпендикулярной плоскости линии, необходимо найти общую точку пересечения для рассматриваемых геометрических объектов. Ее координаты и будут проекцией P. Поскольку они должны удовлетворять обоим равенствам (для прямой и для плоскости), то задача сводится к решению соответствующей системы линейных уравнений.
Понятие проекции часто используется при изучении чертежей. На них изображаются боковые и горизонтальные проекции детали на плоскости zy, zx, и xy.
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Вычисление расстояния от плоскости до точки
Как выше было отмечено, знание координат проекции на плоскость точки позволяет определить дистанцию между ними. Используя обозначения, введенные в предыдущем пункте, получаем, что искомое расстояние равно длине отрезка PQ. Для его вычисления достаточно найти координаты вектора PQ¯, а затем рассчитать его модуль по известной формуле. Конечное выражение для d расстояния между P точкой и плоскостью принимает вид:
d = |PQ¯| = √((x2 — x1)2 + (y2 — y1)2 + (z2 — z1)2).
Полученное значение d представлено в единицах, в которых задается текущая декартова координатная система xyz.
Видео:Проецирование точки на 3 плоскости проекцийСкачать

Пример задачи
Допустим, имеется точка N(0; -2; 3) и плоскость, которая описывается следующим уравнением:
Следует найти точки проекцию на плоскость и вычислить между ними расстояние.
В первую очередь составим уравнение прямой, которая пересекает плоскость под углом 90o. Имеем:
(x; y; z) = (0; -2; 3) + λ*(2; -1; 1).
Записывая это равенство в явном виде, приходим к следующей системе уравнений:
Подставляя значения координат из первых трех равенств в четвертое, получим значение λ, определяющее координаты общей точки прямой и плоскости:
2*(2*λ) — (-2 — λ) + λ + 3 + 4 = 0 =>
Подставим найденный параметр в уравнение прямой и найдем координаты проекции исходной точки на плоскость:
(x; y; z) = (0; -2; 3) + 1,5*(2; -1; 1) = (3; -3,5; 4,5).
Для вычисления дистанции между заданными в условии задачи геометрическими объектами применим формулу для d:
d = √((3 — 0 )2 + (-3,5 + 2 )2 + (4,5 — 3 )2) = 3,674.
В данной задаче мы показали, как находить проекцию точки на произвольную плоскость и как вычислять между ними расстояние.
📹 Видео
Как найти проекцию точки на прямую. Линейная алгебраСкачать

проекции точкиСкачать

Математика это не ИсламСкачать

Прямоугольная система координат. Координатная плоскость. 6 класс.Скачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Координаты на плоскости и в пространстве. Вебинар | МатематикаСкачать

Космическая граница, способная запечатать нас на Земле на долгие поколенияСкачать

Уравнение плоскости. 11 класс.Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Лекция 2. Плоскость. Точка и прямая в плоскости.Скачать