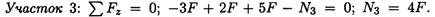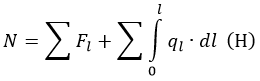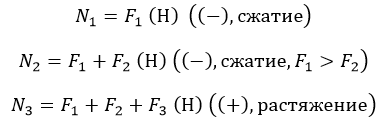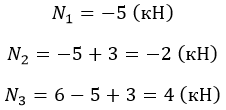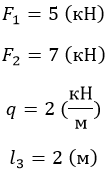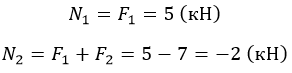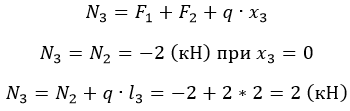Уравнение продольной силы в сечении методом (8 видео)

Продольная сила — внутренний силовой фактор

Приветствую тебя, читатель портала о сопромате и не только – SoproMats. В сегодняшней статье поговорим о таком важном внутреннем силовом факторе как продольная сила. Расскажем, что это за сила, зачем нужна и все в таком духе. Обещаем максимально подробно раскрыть данную тему, а также дать ссылки на смежные статьи, которые касаются продольной силы. Например, укажем ссылку, где можно почитать о построении эпюры распределения продольных сил и т.д.

Содержание

Что такое продольная сила?
Зачем нужна?
Как определяется?
Как обозначается?
В чем измеряется?
Полезные статьи о продольной силе
Построение эпюры
Продольная сила. Метод сечений. Эпюры продольных сил
Внутренние силы при растяжении-сжатии
Пример определения внутренних сил.
Напряжения. Действующие и допускаемые напряжения
$sigma = frac$
Абсолютная и относительная деформация
Построение эпюр продольных сил — формулы, условия и примеры решения задач
Основные понятия
Что такое эпюра продольных сил
Как построить эпюру продольных сил
Пример построения эпюр и решения задач
Заключение
📺 Видео

Видео:РАСТЯЖЕНИЕ-СЖАТИЕ. Построение эпюр. Сопромат.Скачать

Что такое продольная сила?

Продольная сила – это внутренний силовой фактор, который возникает в поперечных сечениях элементов, работающих на центральное растяжение (сжатие). Конечно, продольная сила может возникать не только в элементах, которые работают только на растяжение и сжатие. Она может возникать в сечениях, как ОДИН ИЗ силовых факторов, совместно с поперечной силой или изгибающим моментом. Но это все возможно при сложных видах сопротивления конструкций. В данном уроке мы будем говорить только о чистом растяжении или сжатии.

Зачем нужна?

Этот силовой фактор используется в расчетах на прочность и жесткость элементов конструкций, работающих на растяжение (сжатие). Зная продольную силу можно определить нормальные напряжения в поперечных сечениях элементов, после чего подобрать их размеры, которые бы удовлетворяли условию безопасной прочности, либо проверить прочность, если размеры элемента изначально заданы. Также можно определить осевые перемещения поперечных сечений, после чего сделать вывод о жесткости детали.

Как определяется?

Как и другие внутренние силовые факторы, продольная сила определяется методом сечений. Для того чтобы определить продольную силу в произвольном сечении элемента, его мысленно рассекают в этом сечении на две части, рассматриваются равновесие одной из частей, заменив действие отброшенной части продольной силой. Из уравнения статики, в частности, суммы проекций на одну из осей, выражается продольное усилие. Для построения эпюр, эту процедуру проводят несколько раз, для каждого участка стержня (бруса). Более детально этот процесс рассмотрим ниже, когда будем изучать подробный способ построения эпюры.

Как обозначается?

Продольная сила обозначается буквой N с индексом, который совпадает с названием продольной оси, направленной в сторону растяжения или сжатия нагруженного элемента и перпендикулярной поперечным сечениям. Чаще всего, эта ось обозначается буквой – x. Потому в нашем уроке будем использовать обозначение продольной силы — N_x.

В чем измеряется?

Продольная сила, как и обычные внешние сосредоточенные силы, измеряется в ньютонах. На практике, в расчетах используются килоньютоны (кН). Также иногда в литературе можно встретить размерность – кгс и тс.

Видео:Тех.Мех. - это просто. 1 Метод сеченийСкачать

Полезные статьи о продольной силе

Здесь буду публиковать ссылки на полезные статьи, которые тесно связанны с продольной силой.

Построение эпюры

В этой статье, про построение эпюр продольных сил, Вы узнаете, как рассчитывается эпюра продольных сил на примере ступенчатого бруса, на который действуют различные виды нагрузок. Кроме того, в ней рассмотрено три методики расчета, что позволит всесторонне разобраться в этом вопросе.

Видео:Сопромат. Часть 1. Растяжение (сжатие). Построение эпюр продольных сил и нормальных напряжений.Скачать

Продольная сила. Метод сечений. Эпюры продольных сил

Видео:2013 1 Метод сечений Часть 1Скачать

Внутренние силы при растяжении-сжатии

Центральное растяжение-сжатие возникает в случае, когда на концах стержня вдоль его оси действуют две равные противоположно направленные силы. При этом в каждом сечении по длине стержня возникает внутреннее усилие ( продольная сила $N$ кН), которая численно равна сумме всех сил, которые действуют вдоль оси стержня и расположены с одной стороны от сечения.

Из условий равновесия отсеченной части стержня $N = F$.

Продольная сила при растяжении считается положительной, при сжатии – отрицательной .

Пример определения внутренних сил.

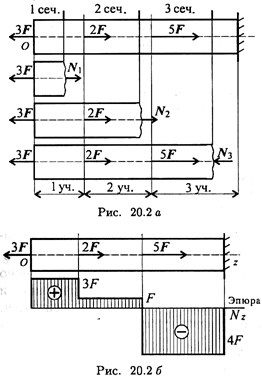
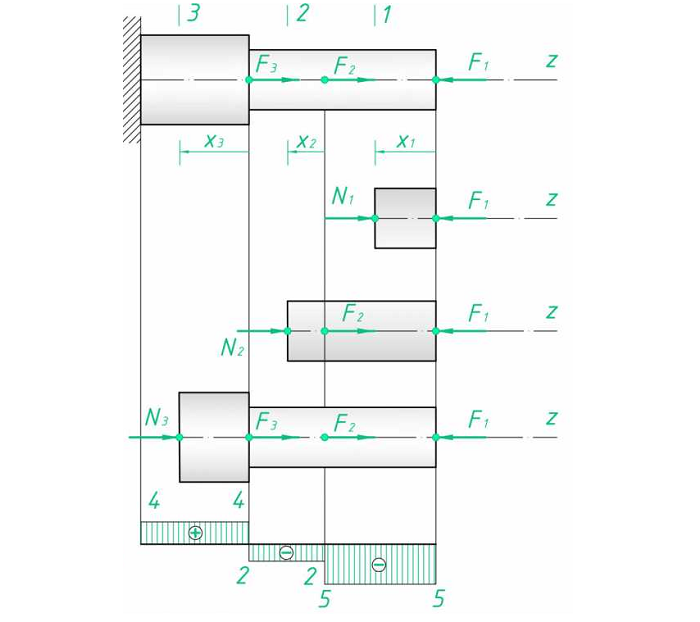
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а). Делим брус на участки нагружения.

Участком нагружения считают часть бруса между внешними силами.

На представленном рисунке 3 участка нагружения.

Воспользуемся методом сечений и определим внутренние силовые факторы внутри каждого участка.

Расчет начинаем со свободного конца бруса, чтобы не определять величины реакций в опорах.

Продольная сила положительна, участок 1 растянут.

Продольная сила положительна, участок 2 растянут.

Продольная сила отрицательна, участок 3 сжат.

Полученное значение N₃ равно реакции в заделке.

Под схемой бруса строим эпюру продольной силы (рис. 20.2, б).

Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.

Ось эпюры параллельна продольной оси.

Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз.

В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.

Напряжения. Действующие и допускаемые напряжения

Величина внутренней силы дает представление о сопротивлении поперечного сечения в целом (интегрально), но не дает представления об интенсивности работы материала в отдельных точках сечения. Так, при равной продольной силе материал в стержне с большим сечением будет работать менее интенсивно, менее напряженно чем меньший.

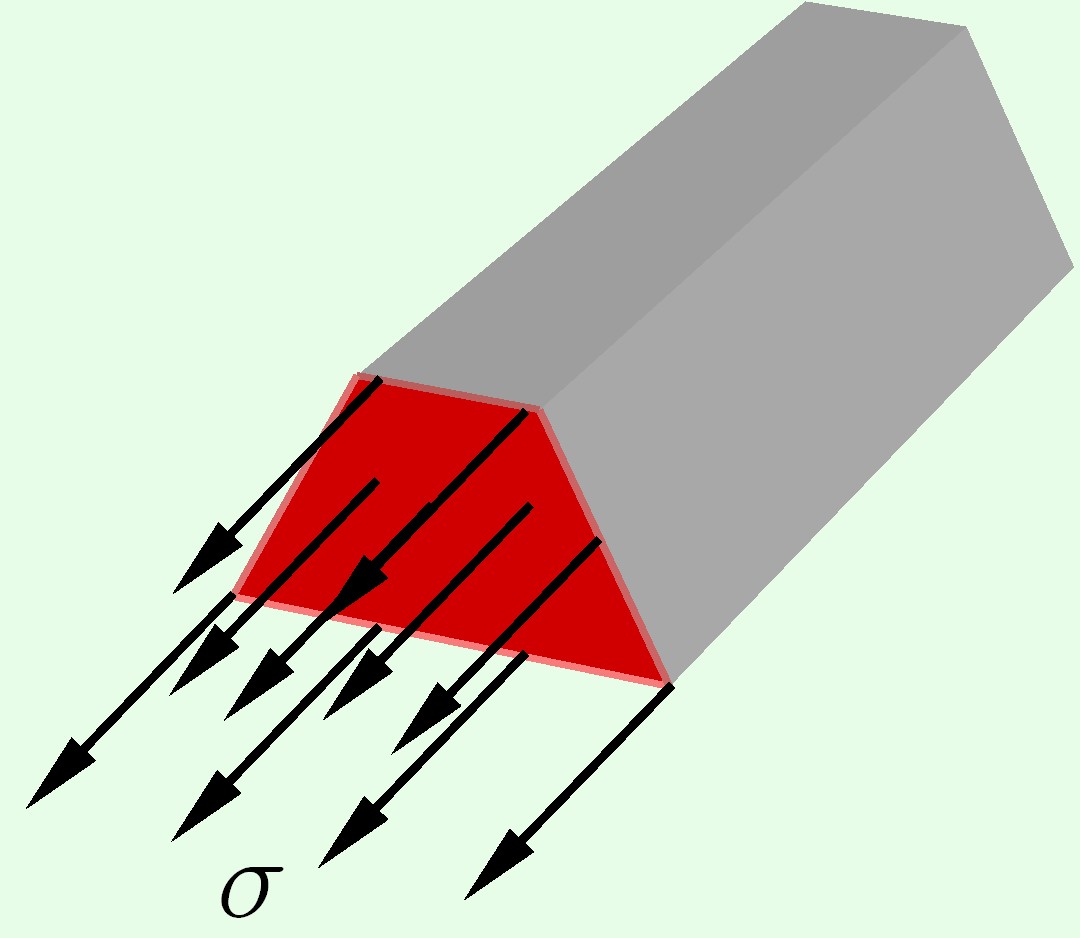
Напряжения – внутренние силы, приходящиеся на единицу площади сечения. Напряжения, направленные перпендикулярно (по нормали) к сечению называются нормальными .

Видео:Внутренние силы. Определение. Метод сечений. Сопромат - Тайные Знания 6.Скачать

$sigma = frac$

Единицы измерения напряжений — Па, кПа, МПа.

Знаки напряжений принимают так, как и для продольной силы.

Действующие напряжения — напряжения, которые возникают в рассматриваемом сечении.

Любой стержень в момент разрушения имеет определенные напряжения, которые зависят только от материала стержня и не зависят от площади сечения.

Допускаемые напряжения $left[ sigma right]$ – такие напряжения, которые не должны быть превышены в запроектированных конструкциях. Допустимые напряжения зависят от прочности материала, характера его разрушения, степени ответственности конструкции.

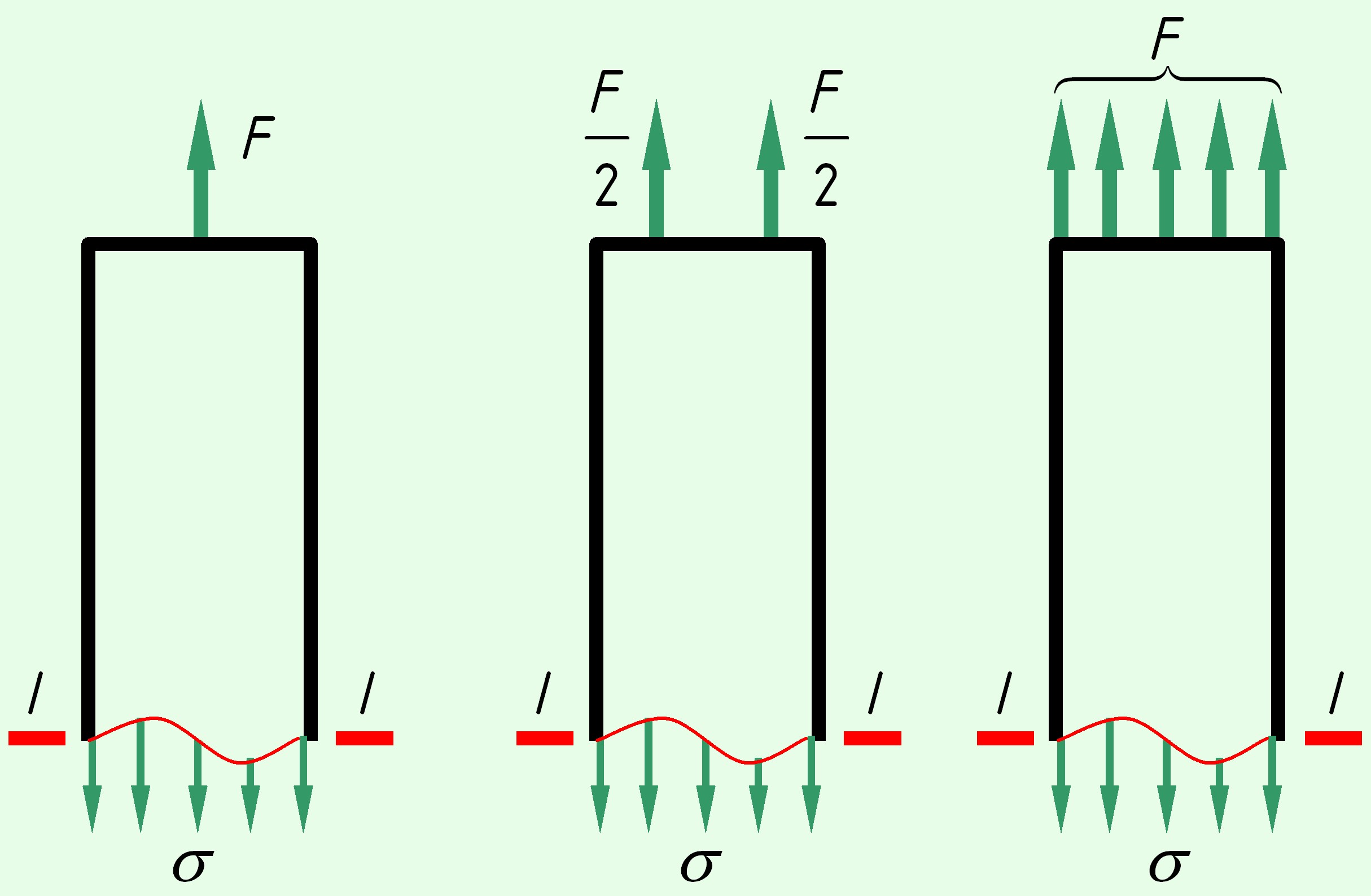
Принцип Сен-Венана : в сечениях, достаточно удаленных от места приложения нагрузки, распределение напряжений не зависит от способа приложения нагрузки, а зависит только от его равнодействующей.

то есть, распределение напряжений в сечении I-I для трех различных случаев, показанных на рисунке, принимается одинаковым.

Рисунок — иллюстрация принципа Сен-Венана

Видео:Основы Сопромата. Внутренние силы. Эпюры внутренних усилий для пространственного стержняСкачать

Абсолютная и относительная деформация

При растяжении возникает удлинение стержня – разница между длиной стержня до и после погрузки. Эта величина называется абсолютной деформацией .

Относительная деформация – отношение абсолютной деформации к первоначальной длине.

$sigma = E cdot varepsilon $

Таблица — физико-механические характеристики материалов

Видео:Метод сеченийСкачать

Построение эпюр продольных сил — формулы, условия и примеры решения задач

Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.

Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.

Но всему свое время. Сначала немного о терминах.

Видео:Сопротивление материалов. Лекция: метод сеченийСкачать

Основные понятия

Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.

Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.

Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.

В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).

Видео:Определение усилий в ферме. Метод сечений. СтроймехСкачать

Что такое эпюра продольных сил

Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.

Видео:Определение усилий, напряжений и перемещений. СопроматСкачать

Как построить эпюру продольных сил

Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.

Сопротивление рассчитывается по формуле:

F_l – действующие на участке l силы (Н);

q_l – распределенные нагрузки (Н/м).

1. Рисуется схема балки и механизмов закрепления;

2. Производится разделение на участки;

3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:

Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;

4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.

Рис. 1. Эпюра продольных сил

Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.

Видео:СМ -1.7 Метод сечений, внутренние силовые факторы (ВСФ)Скачать

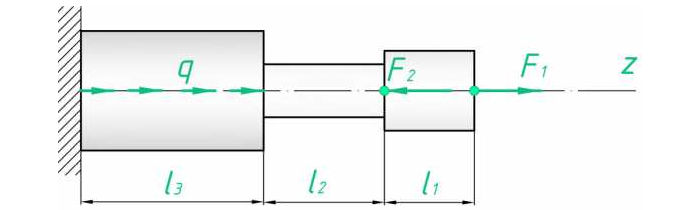
Пример построения эпюр и решения задач

Построить эпюру сил для следующего случая (рис. 2):

Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:

Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N₂ будет постепенно увеличиваться/уменьшаться в зависимости от знака q.

Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l₃ и ql₃ (в масштабе). Поскольку распределение линейно.

По полученным данным строим эпюру (рис. 3).

Видео:Понимание напряжений в балкахСкачать

Заключение

Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.

В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.