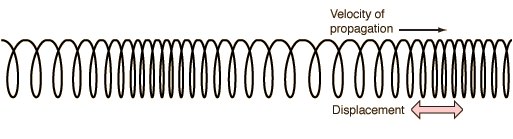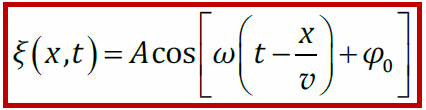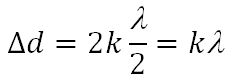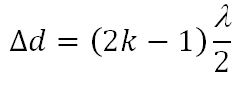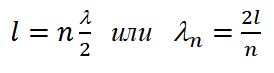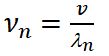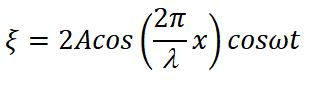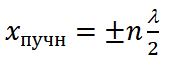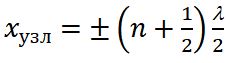Уравнение продольной и поперечной волны (5 видео)

Содержание

Механические волны.
Продольные и поперечные волны.
Продольные и поперечные волны
Продольные волны
Поперечные волны
Уравнение продольной и поперечной волны
Примеры задач с решением
Уравнение продольной и поперечной волны
📸 Видео

Видео:Продольные и поперечные волныСкачать

Механические волны.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: механические волны, длина волны, звук.

Механические волны — это процесс распространения в пространстве колебаний частиц упругой среды (твёрдой, жидкой или газообразной).

Наличие у среды упругих свойств является необходимым условием распространения волн: деформация, возникающая в каком-либо месте, благодаря взаимодействию соседних частиц последовательно передаётся от одной точки среды к другой. Различным типам деформаций будут соответствовать разные типы волн.

Видео:Распространение колебаний в среде. Волны | Физика 9 класс #28 | ИнфоурокСкачать

Продольные и поперечные волны.

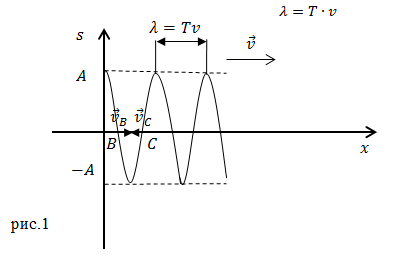
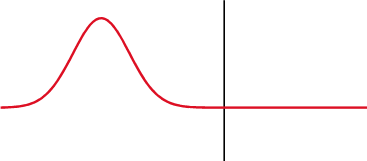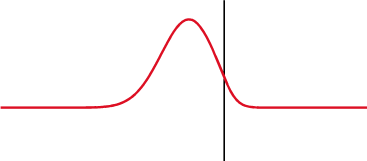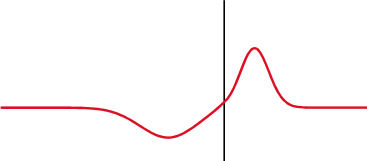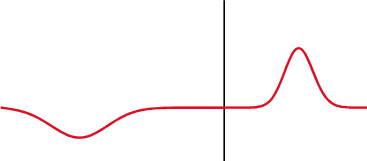
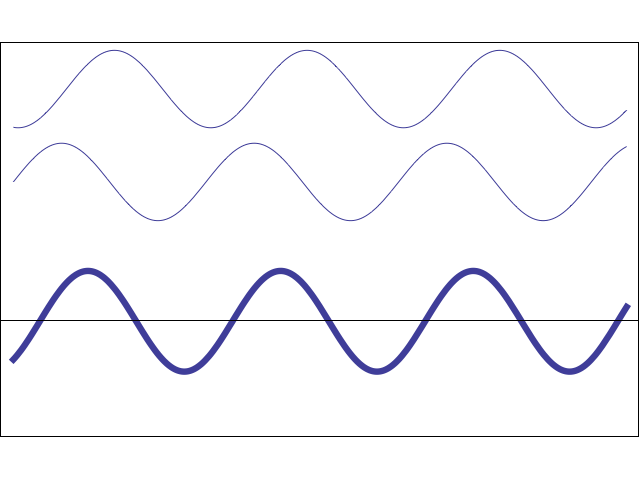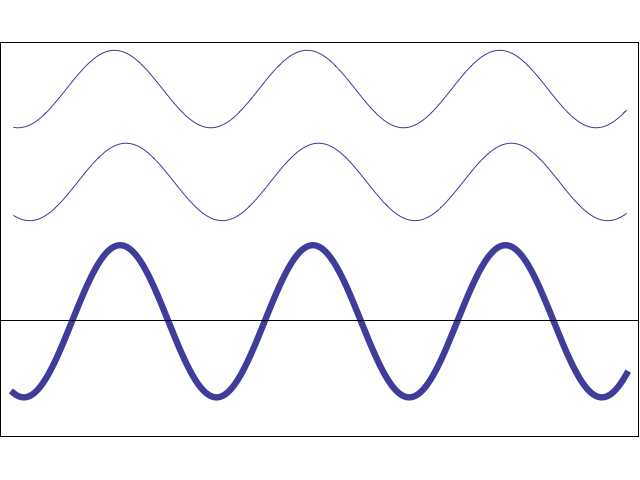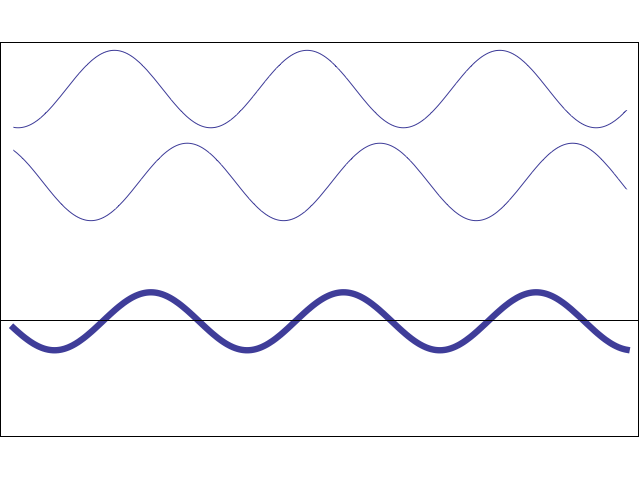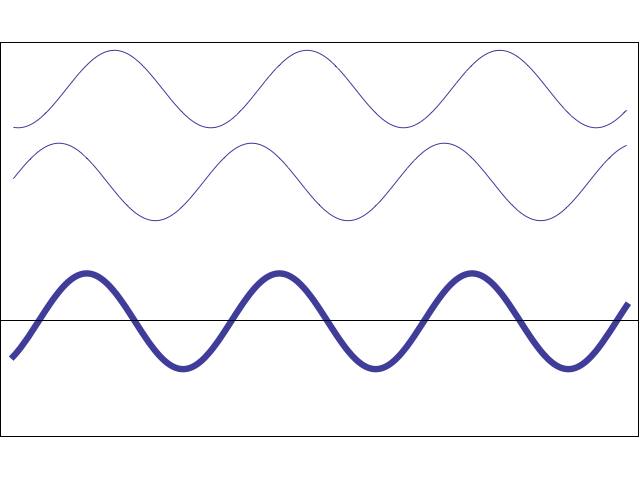
Волна называется продольной, если частицы среды колеблются параллельно направлению распространения волны. Продольная волна состоит из чередующихся деформаций растяжения и сжатия. На рис. 1 показана продольная волна, представляющая собой колебания плоских слоёв среды; направление, вдоль которого колеблются слои, совпадает с направлением распространения волны (т. е. перпендикулярно слоям).

Рис. 1. Продольная волна

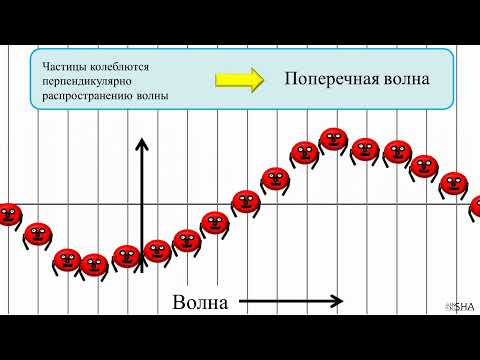
Волна называется поперечной, если частицы среды колеблются перпендикулярно направлению распространения волны. Поперечная волна вызывается деформациями сдвига одного слоя среды относительно другого. На рис. 2 каждый слой колеблется вдоль самого себя, а волна идёт перпендикулярно слоям.

Рис. 2. Поперечная волна

Продольные волны могут распространяться в твёрдых телах, жидкостях и газах: во всех этих средах возникает упругая реакция на сжатие, в результате которой появятся бегущие друг за другом сжатия и разрежения среды.

Однако жидкости и газы, в отличие от твёрдых тел, не обладают упругостью по отношению к сдвигу слоёв. Поэтому поперечные волны могут распространяться в твёрдых телах, но не внутри жидкостей и газов*.

Важно отметить, что частицы среды при прохождении волны совершают колебания вблизи неизменных положений равновесия, т. е. в среднем остаются на своих местах. Волна, таким образом, осуществляет
перенос энергии, не сопровождающийся переносом вещества.

Наиболее просты для изучения гармонические волны. Они вызываются внешним воздействием на среду, меняющимся по гармоническому закону. При распространении гармонической волны частицы среды совершают гармонические колебания с частотой, равной частоте внешнего воздействия. Гармоническими волнами мы в дальнейшем и ограничимся.

Рассмотрим процесс распространения волны более подробно. Допустим, что некоторая частица среды (частица ) начала совершать колебания с периодом . Действуя на соседнюю частицу она потянет её за собой. Частица в свою очередь, потянет за собой частицу и т. д. Так возникнет волна, в которой все частицы будут совершать колебания с периодом .

Однако частицы имеют массу, т. е. обладают инертностью. На изменение их скорости требуется некоторое время. Следовательно, частица в своём движении будет несколько отставать от частицы , частица будет отставать от частицы и т. д. Когда частица пустя время завершит первое колебание и начнёт второе, своё первое колебание начнёт частица , находящаяся от частицы на некотором расстоянии .

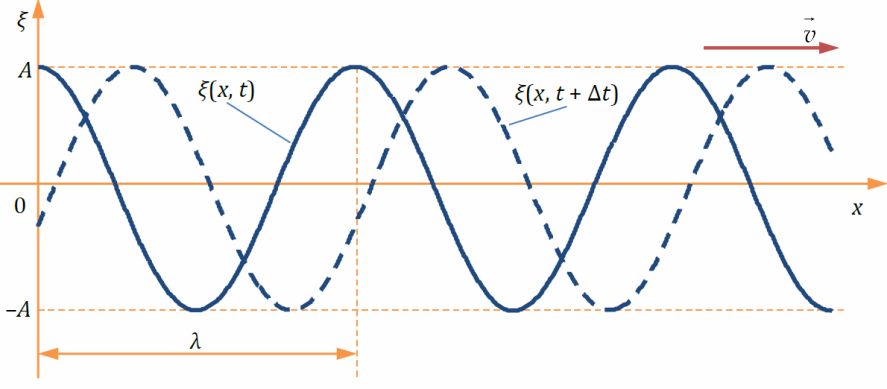
Итак, за время, равное периоду колебаний частиц, возмущение среды распространяется на расстояние . Это расстояние называется длиной волны. Колебания частицы будут идентичны колебаниям частицы колебания следующей частицы будут идентичны колебаниям частицы и т. д. Колебания как бы воспроизводят себя на расстоянии можно назвать пространственным периодом колебаний; наряду с временным периодом она является важнейшей характеристикой волнового процесса. В продольной волне длина волны равна расстоянию между соседними сжатиями или разрежениями (рис. 1 ). В поперечной — расстоянию между соседними горбами или впадинами (рис. 2 ). Вообще, длина волны равна расстоянию (вдоль направления распространения волны) между двумя ближайшими частицами среды, колеблющимися одинаково (т. е. с разностью фаз, равной ).

Скоростью распространения волны называется отношение длины волны к периоду колебаний частиц среды:

Частотой волны называется частота колебаний частиц:

Отсюда получаем связь скорости волны, длины волны и частоты:

На поверхности жидкости могут существовать волны особого типа, похожие на поперечные — так называемые поверхностные волны. Они возникают под действием силы тяжести и силы поверхностного натяжения.

Звуковыми волнами в широком смысле называются всякие волны, распространяющиеся в упругой среде. В узком смысле звуком называют звуковые волны в диапазоне частот от 16 Гц до 20 кГц, воспринимаемые человеческим ухом. Ниже этого диапазона лежит область инфразвука, выше — область ультразвука.

К основным характеристикам звука относятся громкость и высота.
Громкость звука определяется амплитудой колебаний давления в звуковой волне и измеряется в специальных единицах —децибелах (дБ). Так, громкость 0 дБ является порогом слышимости, 10 дБ — тиканье часов, 50 дБ — обычный разговор, 80 дБ — крик, 130 дБ — верхняя граница слышимости (так называемый болевой порог).

Тон — это звук, который издаёт тело, совершающее гармонические колебания (например, камертон или струна). Высота тона определяется частотой этих колебаний: чем выше частота, тем выше нам кажется звук. Так, натягивая струну, мы увеличиваем частоту её колебаний и, соответственно, высоту звука.

Скорость звука в разных средах различна: чем более упругой является среда, тем быстрее в ней распространяется звук. В жидкостях скорость звука больше, чем в газах, а в твёрдых телах — больше, чем в жидкостях.
Например, скорость звука в воздухе при равна примерно 340 м/с (её удобно запомнить как «треть километра в секунду»)*. В воде звук распространяется со скоростью около 1500 м/с, а в стали — около 5000 м/с.
Заметим, что частота звука от данного источника во всех средах одна и та же: частицы среды совершают вынужденные колебания с частотой источника звука. Согласно формуле (1) заключаем тогда, что при переходе из одной среды в другую наряду со скоростью звука изменяется длина звуковой волны.

Видео:🌊 Продольные и поперечные волны ⚛ ФизикаСкачать

Продольные и поперечные волны

Отвлечемся от внутреннего строения вещества для того, чтобы исследовать законы распространения механических волн. Вещество будем рассматривать как сплошную среду, непрерывно изменяющуюся в пространстве.

Частицей, изучая колебания, будем называть малый элемент объема среды, размеры которого много больше, чем расстояния между молекулами, при этом частицу среды принимаем за материальную точку.

Рассматривая механические волны, будем считать вещества, в которых они распространяются, упругими, внутренние силы, возникающие в них при малых деформациях, пропорциональными величине деформации.

При возбуждении колебания, в каком- либо месте упругой среды, в результате взаимодействия частиц среды, оно распространяется в веществе от точки к точке с некоторой конечной скоростью. Процесс распространения колебаний называют волной. Важным свойством волнового процесса является то, что в нем не происходит переноса массы, каждая частица выполняет колебания около положения равновесия. В волне от частицы к частице передается состояние колебательного движения и энергия колебаний. Волна переносит энергию.

В зависимости от направления колебаний частицы вещества по отношению к направлению распространения волны, волны делят на продольные и поперечные.

Видео:Распространение колебаний в упругих средах Продольные и поперечные волны convertedСкачать

Продольные волны

Если частицы совершают колебания в направлении распространения волны, то такую волну называют продольной.

Продольные волны распространяются в веществе, в котором возникают силы упругости, при деформации растяжения и сжатия в веществе в любом агрегатном состоянии.

Так, например, волны звука, распространяющиеся в воздухе, относят к продольным волнам. Продольные волны, имеющие частоты от 17 до 20

000 Гц называют звуковыми. Скорость распространения акустических волн зависит от свойств среды и ее температуры.

При распространении продольной волны в среде возникают чередования сгущений и разрежений частиц, перемещающихся в направлении распространения волны со скоростью $v$. Все время существования волны, элементы среды выполняют колебания у своих положений равновесия, при этом разные частицы совершают колебания со сдвигом по фазе. В твердых телах скорость распространения продольных волн больше, чем скорость поперечных волн.

Скорость распространения продольных упругих волн в однородных в газах или жидкостях равна:

где $K$ — модуль объемной упругости вещества; $rho =const$ — плотность среды. В газах формула (1) справедлива, если избыточное давление много меньше, чем равновесное давление невозмущенного газа.

Скорость распространения продольных волн в тонком стержне, вызванных его продольным растяжением и сжатием равна:

где $E$ — модуль Юнга вещества стержня.

Видео:ФИЗИКА 9 класс: Волны: продольные и поперечные | ВидеоурокСкачать

Поперечные волны

Поперечной волной называют такую волну, в которой колебания частиц среды происходят в направлениях перпендикулярных к направлению распространения волны.

Механические волны могут быть поперечными только в среде, в которой возможны деформации сдвига (среда обладает упругостью формы). Следовательно, в жидкостях и газах механических поперечных волн не наблюдают. Поперечные механические волны возникают в твердых телах. Примером таких волн являются волны, которые распространяются в натянутых струнах.

Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде можно вычислить как:

где $G$ — модуль сдвига среды; $rho $ — плотность вещества.

Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.

Приведенная здесь скорость распространения упругих волн называется фазовой скоростью.

Видео:Урок 95 (осн). Механические волны. ЗвукСкачать

Уравнение продольной и поперечной волны

Основной задачей при изучении волн является установление закона изменения во времени и пространстве физических величин, которые однозначно характеризуют движение волны. При рассмотрении упругих волн такой величиной служит, например, смещение ($s$) частиц среды от их положений равновесия. Функция $s$ в зависимости от координат пространства и времени называется уравнением волны.

Самым простым видом волн являются гармонические волны. В таких волнах параметры $s$ для всех частиц среды, которые охвачены волной, совершают гармонические колебания с одинаковыми частотами. Для реализации данного волнового процесса необходимо, чтобы источник гармонических волн совершал незатухающие гармонические колебания.

Уравнение одномерной волны записывают как:

$k$ — волновое число; $lambda $ — длина волны; $A$ — амплитуда волны в точке (если среда не поглощает энергию, то амплитуда колебаний совпадает с амплитудой колебаний источника волн); $left[omega t-kx+varphi right]$ — фазой волны; $omega $- циклическая частота колебаний; $varphi $ — начальная фаза.

Видео:Механические модели волн. 1.Скачать

Примеры задач с решением

Задание: Поперечная волна распространяется по натянутой струне со скоростью $v=2frac$, период колебаний точек струны равен T= 1 с, амплитуда колебаний составляет 0,05 м. Какими будут смещение и скорость малого элемента струны, который находится на расстоянии $x_1=1 $м от источника колебаний в момент времени $t_1$=2 c?

Решение: Основой для решения задачи служит уравнение одномерной волны:

где $s$ — смещение точки струны, совершающей колебания; $x$ — расстояние от источника волны до рассматриваемой точки; $k=frac$ — волновое число; $v$ — скорость распространения волны.

Циклическую частоту $omega $ найдем (при T=1 c) как:

Тогда волновое число при $v=2frac$ равно:

Уравнение для нашей волны в учетом данных задачи приобретет вид:

Смещение точки струны, находящейся на расстоянии $x_1=1 $м от источника колебаний в момент времени $t_1$=2 c будет равно:

Скорость рассматриваемой точки струны найдем как:

Ответ: $s_1=-0,05$ м; $frac

left(t_1, x_1right)$=0$frac$

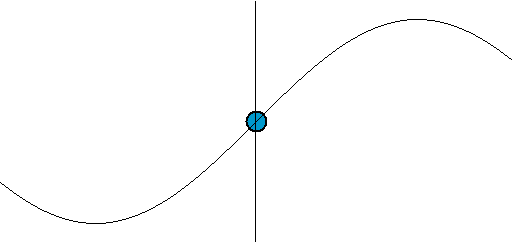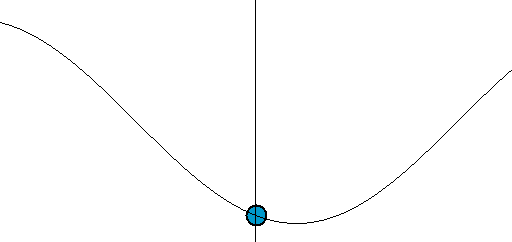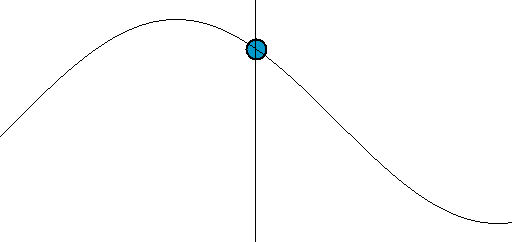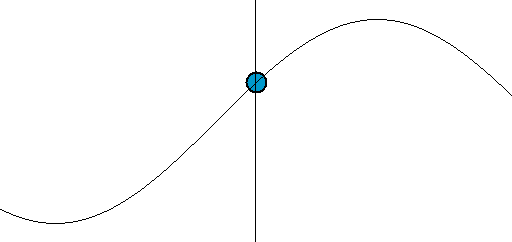
Задание: Плоская одномерная волна распространяется в упругой среде. Изобразите на графике направление скорости частиц среды в точках $s=0, $при t=0 для продольной и поперечной волн.

Решение: Уравнением одномерной плоской волны служит выражение:

При $t=0 c$ из выражения (2.1) получаем:

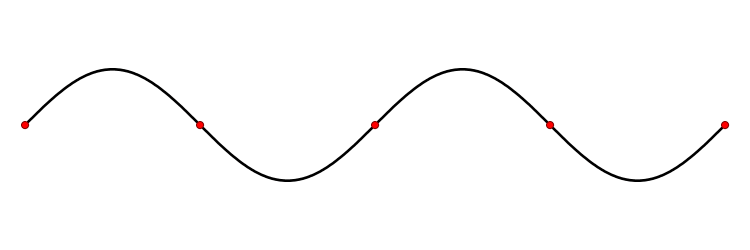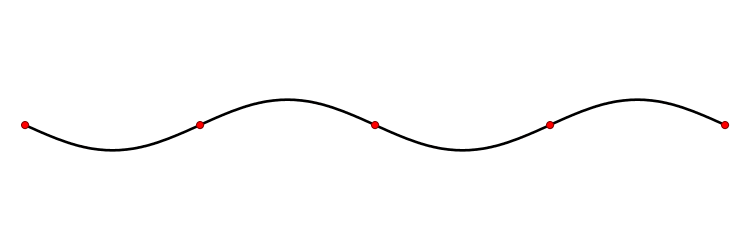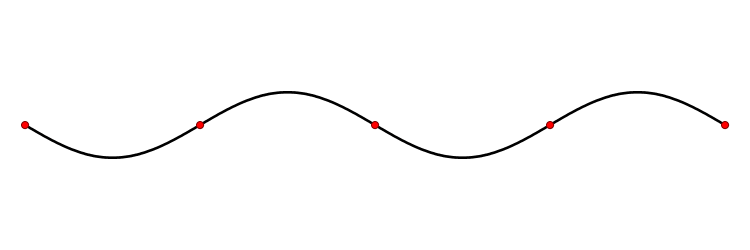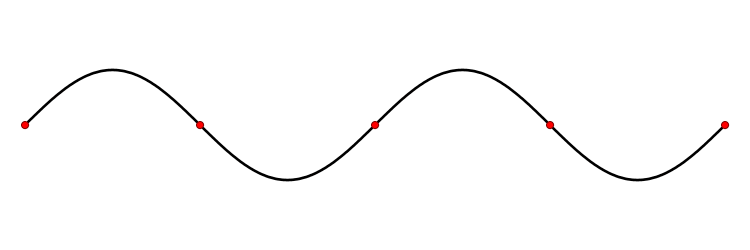
В продольной волне частицы смещаются вдоль направления скорости движения волны (рис.1).

В продольной волне частицы совершают колебания поперек направления скорости движения волны рис.2.

Видео:Физика 11 класс (Урок№2 - Механические волны.)Скачать

Уравнение продольной и поперечной волны

Для существования волны необходим источник колебания и материальная среда или поле, в которых эта волна распространяется. Волны бывают самой разнообразной природы, но они подчиняются аналогичным закономерностям.

По физической природе различают:

упругие, звуковые, волны на поверхности жидкости

свет, радиоволны, излучения

По ориентации возмущений различают:

Смещение частиц происходит вдоль направления распространения;

могут распростаняться только в упругих средах;

необходимо наличие в среде силы упругости при сжатии;

могут распространяться в любых средах.

Смещение частиц происходит поперек направления распространения;

могут распростаняться только в упругих средах;

необходимо наличие в среде силы упругости при сдвиге;

могут распространяться только в твердых средах (и на границе двух сред).

Примеры: упругие волны в струне, волны на воде

По характеру зависимости от времени различают:

Упругие волны — механические возмещения (деформации), распространяющиеся в упругой среде. Упругая волна называется гармонической (синусоидальной), если соответствующие ей колебания среды являются гармоническими.

Бегущие волны — волны, переносящие энергию в пространстве.

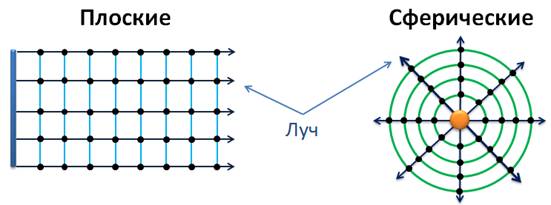
По форме волновой поверхности: плоская, сферическая, цилиндрическая волна.

Волновой фронт — геометрическое место точек, до которых дошли колебания к данному моменту времени.

Волновая поверхность — геометрическое место точек, колеблющихся в одной фазе.

Характеристики волны

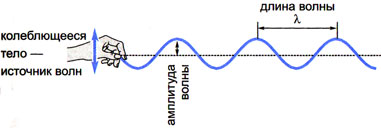
Длина волны λ — расстояние, на которое волна распространяется за время, равное периоду колебаний

Амплитуда волны А — амплитуда колебаний частиц в волне

Скорость волны v — скорость распространения возмущений в среде

Период волны Т — период колебаний

Частота волны ν — величина, обратная периоду

Уравнение бегущей волны

В процессе распространения бегущей волны возмущения среды доходят до следующих точек пространства, при этом волна переносит энергию и импульс, но не переносит вещество (частицы среды продолжают колебаться в том же месте пространства).

где v – скорость, φ₀ – начальная фаза, ω – циклическая частота, A – амплитуда

Свойства механических волн

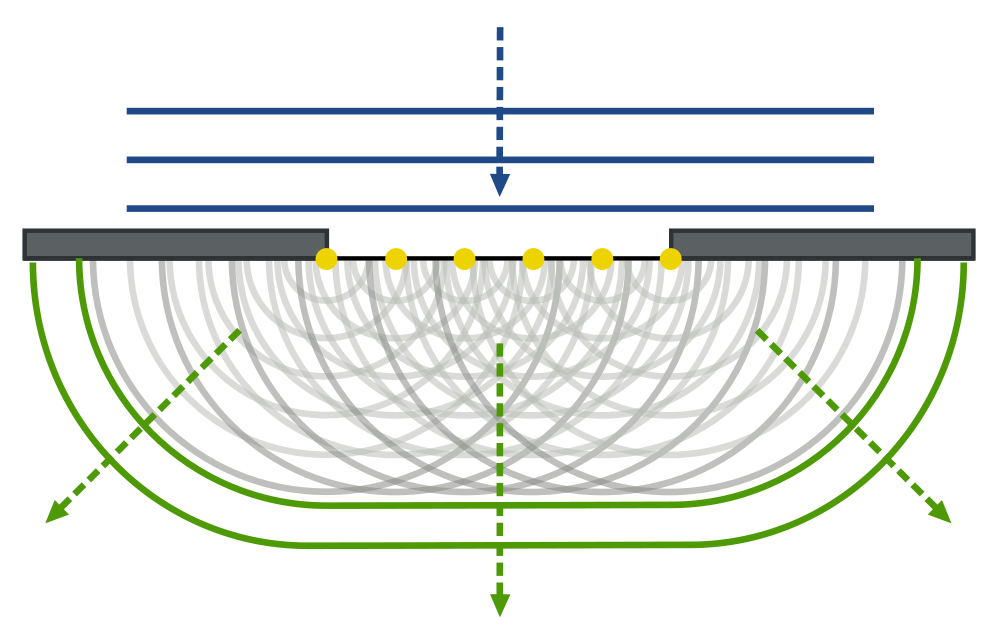
1. Отражение волн – механические волны любого происхождения обладают способностью отражаться от границы раздела двух сред. Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду.

2. Преломление волн – при распространении механических волн можно наблюдать и явление преломления: изменение направления распространения механических волн при переходе из одной среды в другую.

3. Дифракция волн – отклонение волн от прямолинейного распространения, то есть огибание ими препятствий.

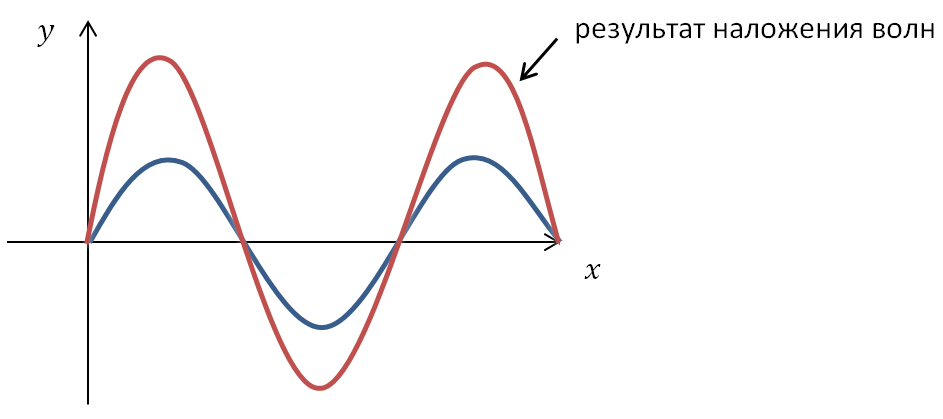
4. Интерференция волн – сложение двух волн. В пространстве, где распространяются несколько волн, их интерференция приводит к возникновению областей с минимальным и максимальным значениями амплитуды колебаний

Интерференция и дифракция механических волн.

Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении.

При наложении волн может наблюдаться явление интерференции. Явление интерференции возникает при наложении когерентных волн.

Когерентными называют волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.

Интерференцией называется постоянное во времени явление взаимного усиления и ослабления колебаний в разных точках среды в результате наложения когерентных волн.

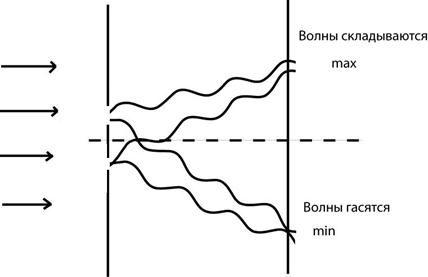
Результат суперпозиции волн зависит от того, в каких фазах накладываются друг на друга колебания.

Если волны от источников А и Б придут в точку С в одинаковых фазах, то произойдет усиление колебаний; если же – в противоположных фазах, то наблюдается ослабление колебаний. В результате в пространстве образуется устойчивая картина чередования областей усиленных и ослабленных колебаний.

Условия максимума и минимума

Если колебания точек А и Б совпадают по фазе и имеют равные амплитуды, то очевидно, что результирующее смещение в точке С зависит от разности хода двух волн.

Если разность хода этих волн равна целому числу волн (т. е. четному числу полуволн) Δd = kλ , где k = 0, 1, 2, . то в точке наложения этих волн образуется интерференционный максимум.

Условие максимума:

Амплитуда результирующего колебания А = 2x₀.

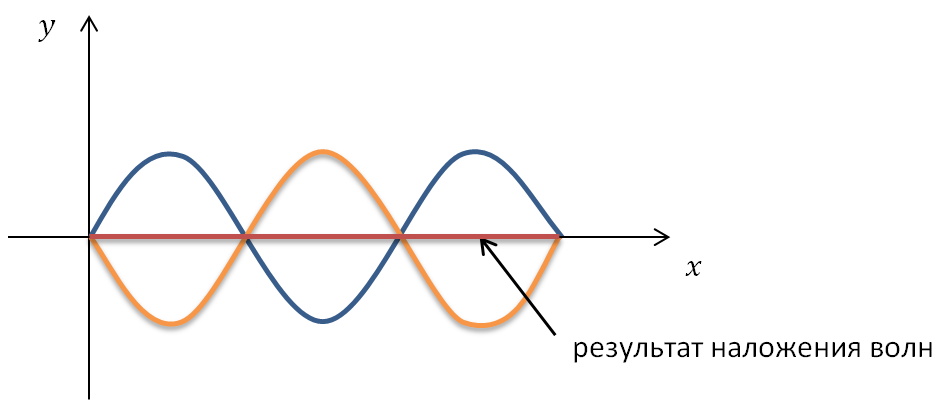
Если разность хода этих волн равна нечетному числу полуволн, то это означает, что волны от точек А и Б придут в точку С в противофазе и погасят друг друга.

Условие минимума:

Амплитуда результирующего колебания А = 0.

Если Δd не равно целому числу полуволн, то 0

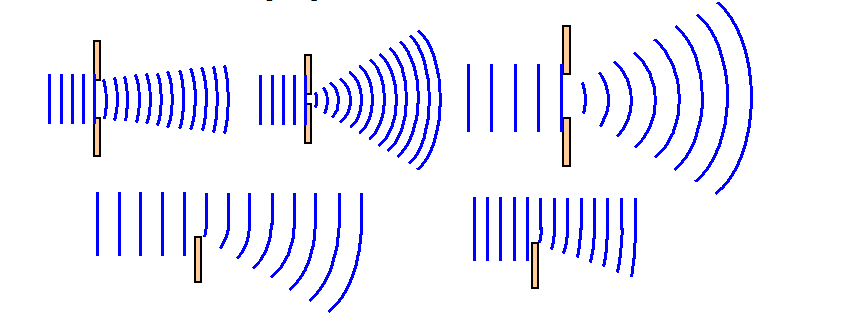
Явление отклонения от прямолинейного распространения и огибание волнами препятствий называется дифракцией.

Соотношение между длиной волны (λ) и размерами препятствия (L) определяет поведение волны. Дифракция наиболее отчетливо проявляется, если длина набегающей волны больше размеров препятствия. Опыты показывают, что дифракция существует всегда, но становится заметной при условии d

Дифракция – общее свойство волн любой природы, которая происходит всегда, но условия её наблюдения разные.

Волна на поверхности воды распространяется в сторону достаточно большого препятствия, за которым образуется тень, т.е. волнового процесса не наблюдается. Такое свойство используется при устройстве волноломов в портах. Если же размеры препятствия сравнимы с длиной волны, то за препятствием будет наблюдаться волнение. Позади него волна распространяется так, как будто препятствия не было вовсе, т.е. наблюдается дифракция волны.

Примеры проявления дифракции. Слышимость громкого разговора за углом дома, звуки в лесу, волны на поверхности воды.

Стоячие волны

Стоячие волны образуются при сложении прямой и отраженной волны, если у них одинаковая частота и амплитуда.

В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.

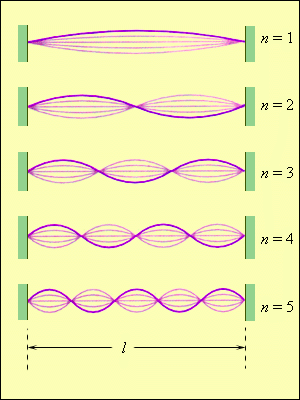
Колебания струны. В закрепленной с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие волны, причем в местах закрепления струны должны располагаться узлы. Поэтому в струне возбуждаются с заметной интенсивностью только такие колебания, половина длины волны которых укладывается на длине струны целое число раз.

Отсюда вытекает условие

Длинам волн соответствуют частоты

n = 1, 2, 3. Частоты v n называются собственными частотами струны.

Гармонические колебания с частотами v n называются собственными или нормальными колебаниями. Их называют также гармониками. В общем случае колебание струны представляет собой наложение различных гармоник.

Уравнение стоячей волны:

В точках, где координаты удовлетворяют условию 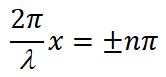(n = 1, 2, 3, …), суммарная амплитуда равна максимальному значению – это пучности стоячей волны. Координаты пучностей:

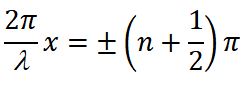
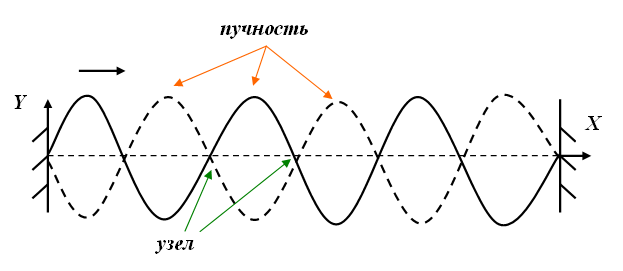
В точках, координаты которых удовлетворяют условию (n = 0, 1, 2,…), суммарная амплитуда колебаний равна нулю – это узлы стоячей волны. Координаты узлов:

Образование стоячих волн наблюдают при интерференции бегущей и отраженных волн. На границе, где происходит отражение волны, получается пучность, если среда, от которой происходит отражение, менее плотная (a), и узел – если более плотная (б).

Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях.

Стоячие волны возникают, например, в закреплённой с обоих концов натянутой струне при возбуждении в ней поперечных колебаний. Причём в местах закреплений располагаются узлы стоячей волны.

Если стоячая волна устанавливается в воздушном столбе, открытом с одного конца (звуковая волна), то на открытом конце образуется пучность, а на противоположном – узел.