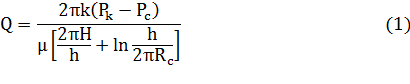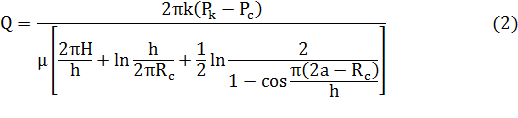PROНЕФТЬ. Профессионально о нефти. – 2017 — № 2(4). – С. 25-30
УДК 622.276.66 СГ
М.В. Симонов, А.П. Рощектаев, к.ф.-м.н.
Научно-Технический Центр «Газпром нефти» (ООО «Газпромнефть НТЦ»)
Ключевые слова: многостадийный гидроразрыв пласта, трещиноватые коллекторы, гидродинамические исследования скважин, десорбция газа
Рассмотрено построение математической модели притока нефти и газа к горизонтальной скважине с множественными трещинами гидроразрыва пласта (ГРП) в трещиноватом низкопроницаемом пласте. На основе предложенной модели была проведена серия численных экспериментов. Полученные результаты позволили выделить несколько режимов течения, характерных для трещиноватого коллектора, разрабатываемого горизонтальными скважинами с многостадийным ГРП. Разработанная модель может быть использована для интерпретации гидродинамических исследований в трещиноватом коллекторе.
- Multifractured horizontal well inflow model for shale gas and oil
- введение
- Физическая модель
- Математическая модель
- Численная реализация
- Сравнение результатов с коммерческим симулятором
- Определение влияния зоны SRV на добычу
- Заключение
- Список литературы
- Reference
- ГЛАВА 2 — УСТАНОВИВШИЙСЯ ПРИТОК РЕАЛЬНОГО ГАЗА К ГОРИЗОНТАЛЬНОЙ СКВАЖИНЕ ПО ЛИНЕЙНОМУ И НЕЛИНЕЙНОМУ ЗАКОНАМ ФИЛЬТРАЦИИ
- Уравнения притока жидкости к скважине.
- 💥 Видео
Видео:Вызов притока и освоение скважин. Методы вызова притока. НефтянкаСкачать

Multifractured horizontal well inflow model for shale gas and oil
PRONEFT». Professional’no o nefti, 2017, no. 2(4), pp. 25-30
M.V. Simonov, A.P. Roschektaev
Gazpromneft NTC LLC, RF, Saint-Petersburg
Keywords: multistage hydraulic fracturing, fractured reservoir, well tests, gas desorbtion
The work refers to construction a mathematical model of the flow of oil and gas fluids to the multifractured in fractured formations. Series of numerical experiments were done based on the proposed model. The obtained results allowed to identify the flow regimes characterizing properties of the fractured reservoir. The developed model can be used to well testing in fractured reservoirs.
Видео:Кривая притока (Слаг тест)Скачать

введение
В последние десятилетия особенный интерес вызывают исследования эксплуатационных характеристик горизонтальных скважин (ГС) после проведения многостадийного гидроразрыва пласта (МГРП) в низкопроницаемых нефтегазовых коллекторах. В настоящее время опубликовано значительное число работ, предлагающих различные модели притока к ГС с МГРП [1–3] . В большинстве предложенных моделей не учитывается образование дополнительной сети трещин, формирующейся за счет активации естественной трещиноватости пласта при проведении операций ГРП.
Кроме отсутствия моделей, качественно описывающих работу ГС с МГРП в трещиноватых коллекторах, следует отметить сложность определения характеристик трещиноватого коллектора с помощью проведения экспериментальных исследований. Для определения характеристик пластов используют методы гидродинамических исследований скважин (ГДИС) [4]. Однако для определения свойств коллектора, на который пробурена ГС с МГРП, установившаяся методика ГДИС отсутствует.
Следует отметить работу [5], посвященную построению композиционной модели пласта после проведения МГРП в ГС. В данной работе рассмотрены физическая и математическая модели притока к ГС с МГРП. Предложена численная схема реализации математической модели методом конечных элементов, и, что особенно важно, выполнены анализ и интерпретация режимов течения к ГС с МГРП в трещиноватом коллекторе. Результаты анализа представлены при работе скважины с постоянным давлением или постоянным дебитом скважины. Выделение характерных режимов позволяет определить свойства трещиноватого коллектора, таким образом решается обратная задача. Однако следует отметить, что авторами работы [5] не учитывалось изменение дебита в трещинах ГРП при работе скважины с постоянным давлением. Данное допущение приводит к нарушению физики процесса течения в трещинах ГРП.
Бурение ГС с МГРП активно применяется при добыче не только нефти, но и газа, в частности, сланцевого. Для моделирования притока газа к ГС с МГРП соотношения уравнения, представленные в работе [5], не изменятся. Однако при добыче сланцевого газа важно учитывать добычу адсорбированного газа из пор матрицы [6–8]. В работе [6] предложена математическая модель, описывающая течение газа на основе гидродинамического симулятора SIMED II. В данной статье представлено уравнение, описывающее течение газа из адсорбирующих пор в неадсорбирующие (поры матрицы). Авторами было показано влияние учета адсорбированного газа в матрице на общую добычу газа в скважине.
Использование математических моделей, представленных в работах [5, 6], учет недостатков, отмеченных ранее (учет изменения дебита в трещинах ГРП, возможность десорбции газа из пор матрицы), позволили построить корректную математическую модель притока к ГС с МГРП и реализовать ее в виде программного комплекса.
Видео:Проще говоря. Зачем нужны горизонтальные скважины?Скачать

Физическая модель
Модель пласта представляет собой совокупность трех областей: искусственной трещины, затронутая ГРП (Stimulated Reservoir Volume, SRV) [9], не затронутая ГРП (рис. 1). Искусственные трещины распространены вдоль ствола скважины и имеют одинаковые длину и проницаемость. Область, затронутая ГРП – это отрытые и связанные природные трещины. Она состоит из матрицы и микротрещин с различной проницаемостью. Проницаемость матрицы мала по сравнению с проницаемостью микротрещин, течение жидкости между ними определяется разностью давлений между матрицей и микротрещинами. Не затронутая ГРП область обладает теми же характеристиками, что и матрица.
Рис. 1. Физическая модель пласта с ГС с МГРП
Другими важными допущениями являются следующие:
- работа скважины моделируется при постоянном забойном давлении или при постоянном дебите скважины;
- течение — изотермическое;
- сила тяжести не учитывается.
Видео:Геонавигация горизонтальных скважин: Настоящее и БудущееСкачать

Математическая модель
Течение в области трещин ГРП подчиняется закону Дарси
где ϕf – пористость области искусственной трещины; Сf – полная сжимаемость области искусственной трещины, атм -1 (10 МПа -1 ); pf – давление в области искусственной трещины, атм (0,1 МПа); kf – проницаемость области искусственной трещины, мД (10 -3 мкм 2 ); μ – вязкость флюидов, Па⋅с; qf – дебит в области искусственной трещины, м 3 /сут; δ – дельта-функция, равная 1 при M=Mʹ и 0 во всех остальных случаях; M – текущая координата; Mʹ – положение скважины; pi – начальное давление, атм (0,1 МПа); ps – давление области микротрещин, атм (0,1 МПа); Ωf – граница области искусственной трещины, м.
Для области, затронутой ГРП, вводится модель двойной пористости с учетом адсорбции газа в матрице. Течение жидкости в области микротрещин подчиняется закону Дарси
где ϕs, ϕm – пористость соответственно в области микротрещин и матрицы; ks, km – проницаемость соответственно в области микротрещин и матрицы, мД (10 -3 мкм 2 ); pm – давление в матрице, атм (0,1 МПа); Ср – полная сжимаемость области искусственной трещины, атм -1 (10 МПа -1 ); qs – дебит, в области микротрещин, м 3 /сут; α – межпоровый коэффициент течения из матрицы в микротрещины; β – диффузионный коэффициент течения, (β = 1 при ρm > ρs и β = 0 при ρm 3 ; ρm – плотность газа в матрице, кг/м 3 ; ρs – плотность газа в микротрещинах, кг/м 3 ; ym – удельная масса адсорбированного газа по отношению ко всему газу в матрице; Ωin – граница области, затронутой ГРП, м.
Уравнение для матрицы области, не затронутой ГРП, будет идентично уравнению для матрицы области, затронутой ГРП.
где Ωout – внешняя граница пласта, м.
Параметры системы уравнений (1−3) приводятся к безразмерным величинам для дальнейшей численной реализации предложенной модели.
Видео:Ремонт скважины, освоение, вызов притока.Скачать

Численная реализация
Предложенную математическую модель можно реализовать различными численными методами (конечно-разностными, конечных элементов, граничных элементов и др.) [10]. В данной работе выбран метод конечных разностей как наиболее простой для интегрирования дифференциальных уравнений параболического типа. Главной проблемой метода является построение правильной разностной схемы, которая будет сходиться к решению.
Вся расчетная область покрывается расчетной сеткой. В области скважины и трещин ГРП строится сетка с меньшим шагом, чем в остальных областях вследствие большего размера областей. Для решения системы уравнений применяется следующая разностная схема:
где k – номер временного уровня; n, m– номер координаты; Δt – шаг по времени; h – шаг по координате.
В выражении (4) опущены все коэффициенты, а источники обозначены через q.
Представленная численная схема была использована для решения систем уравнений и была реализована на языке С++ в среде программирования Microsoft Visual Studio Express 2013.
Видео:Бурение горизонтальных скважинСкачать

Сравнение результатов с коммерческим симулятором
Для апробации результатов, получаемых в разработанном программном комплексе, было проведено сравнение результатов работы разработанного и коммерческого симуляторов (рис. 2). В коммерческом симуляторе реализованы алгоритмы аналитических моделей скважины и пласта. В него также включена модель горизонтальной скважины с несколькими ГРП для анализа добычи нетрадиционных запасов (модель двойной пористости/проницаемости). Были заданы идентичные параметры работы скважины и свойства пласта. Рассматривались изотропная среда и среда с двойной проницаемостью, без учета десорбции газа из матрицы.
Рис. 2. Сопоставление дебита в логарифмическом масштабе (1, 2) и накопленной добычи (3, 4), полученных в коммерческом симуляторе (1, 3) и разработанном программном модуле (2, 4) для однопоровой среды
Полученные данные показывают хорошее соответствие между результатами, полученными в коммерческом симуляторе и разработанном программном комплексе (относительная погрешность – менее 5 %). Возможности разработанного программного комплекса позволяют получать результаты с учетом различия в свойствах трещин, области, затронутой ГРП, и матрицы.
Видео:Гидродинамические исследования скважинСкачать

Определение влияния зоны SRV на добычу
Были проведены численные эксперименты по моделированию пласта, эксплуатируемого ГС с МГРП, с учетом вышеописанных особенностей. Проведен анализ влияния учета зоны SRV: в первом случае зона SRV идентична матрице, во втором – их свойства различаются (рис. 3).
Рис. 3. Динамика дебита (1, 2) и накопленной добычи (3, 4) с учетом (1, 3) и без учета (2, 4) зоны SRV
Были также проведены численные эксперименты по моделированию изменения забойного давления в ГС с МГРП с учетом влияния зоны SRV. Исследованы режимы течения в пласте. Построена диагностическая зависимость логарифмической производной безразмерного давления от времени в билогарифмических координатах (рис. 4). По виду кривой можно определить режимы течения [4, 5]. Каждый режим течения характеризует дренирование определенной зоны пласта и влияние его границ, трещин и др. При этом необходимо отметить, что в зависимости от свойств коллектора, трещин ГРП и работы скважины, некоторые режимы могут быть не выявлены [3].
Рис. 4. Зависимость логарифмической производной давления от безразмерного времени с выделением режимов течения в билогарифмических координатах с учетом (1) и без учета (2) влияния зоны SRV
В результате двумерного моделирования можно выделить следующие режимы течения в пласте.
- Линейный режим. Приток флюида направлен из трещины в скважину. Этот режим сохраняется и далее, когда начинается приток из микротрещин зоны SRV к трещинам ГРП. Наклон кривой на диагностическом графике равен ½. Возможна также инициализация билинейного режима, когда приток идет одновременно из трещины в скважину и из скважины к трещинам ГРП. Наклон кривой на диагностическом графике в этом случае будет равен ¼.
- Переходный период характеризует начало притока от матрицы к микротрещинам в зоне SRV. Производная давления на диагностическом графике снижается. После выравнивания давления в матрице и микротрещинах пласт ведет себя как однородный.
- Линейный режим течения. Приток направлен от матрицы к области SRV. Данный режим может быть реализован при больших размерах пласта и малых размерах зоны SRV.
- Псевдоустановившийся режим течения возникает, когда возмущение давления достигает границ дренируемого пласта. Наклон кривой давления на диагностическом графике равен 1.
На рис. 5 показано распределение давления в пласте в зависимости от времени работы ГС с МГРП. Из него видно, что после 10 ч работы скважины наиболее существенно изменилось давление в области трещин ГРП, следовательно, дренируется область вблизи трещин ГРП, после 20 ч – изменение давления в пласте достигло границы области SRV, а после 50 и 100 ч – дренировалась уже вся область SRV, через 150 ч – изменение давления вышло за границы области SRV и началось дренирование области, не затронутой SRV, а после 250 ч – изменение давления уже достигло границ пласта.
Рис. 5. Распределение давления в пласте через 10 (а), 20 (б), 50 (в), 100 (г), 150 (д) и 250 (е) ч эксплуатации
Таким образом, определить дренируемую зону пласта можно как по диагностическому графику производной давления, так и по характеру распределения давления в пласте, определяемому по данным расчета.
Все описанные результаты были получены длятечения нефти в пласте, при этом представленную математическую модель (1)–(3) можно использовать для моделирования притока газа к ГС с МГРП. В математическую модель (1)–(3) входят слагаемые, отвечающие за десорбцию газа из пор матрицы, что позволяет провести исследования по определению изменения дебита и забойного давления газовой скважины с учетом и без учета десорбции газа.
Различия в физических свойствах (вязкость, сжимаемость, плотность) газа и их существенная зависимость от давления приводят к необходимости использования вместо давления функций псевдодавления pps и псевдовремени tps [11]. Функции псевдодавления и псевдовремени имеют следующий вид:
где μg – вязкость газа; Z – фактор сжимаемости; Сt – сжимаемость газа; p0 – произвольное давление газа ниже минимального, полученного при численном моделировании.
В данной работе без потери общности принимается p0=0. Вязкость и фактор сжимаемости в зависимости от давления вычисляются по корреляциям при заданном значении плотности газа.
Полученные результаты показывают влияние десорбции газа на дебит и накопленную добычу газа (рис. 6). При моделировании работы скважины с учетом десорбции газа добыча газа и забойное давление увеличиваются по сравнению аналогичными показателями при моделировании без учета десорбции.
Рис. 6. Динамика дебита (1, 2) и накопленной добычи газа (3, 4) с учетом (2, 4) и без учета (1, 3) десорбции газа
Видео:Как бурят горизонтальные скважиныСкачать

Заключение
Разработанная математическая модель (1)−(3) позволяет определять приток к ГС с МГРП с учетом десорбции газа из пор матрицы. Созданный программный комплекс дает возможность получить эксплуатационные характеристики ГС с МГРП в трещиноватых коллекторах. Сравнительный анализ работы разработанного программного комплекса и коммерческого симулятора показал хорошее соответствие результатов. Серия различных численных экспериментов с использованием разработанной математической модели позволила выделить несколько режимов течения, которые являются характерными для трещиноватого коллектора, а также провести оценку степени влияния десорбции газа из пор матрицы на дебит газовой скважины и изменение забойного давления. Разработанное программное обеспечение может быть использовано для определения параметров трещиноватого пласта, свойств и размеров зоны SRV, характеристик трещин ГРП при интерпретации результатов ГДИС и получения данных о распределении давления в пласте.
Видео:Метод Хорнера при интерпретации данных ГДИССкачать
Список литературы
- Qanbari F. & Clarkson C.R. Production Data Analysis of Multi-Fractured Horizontal Wells Producing from Tight Oil Reservoirs — Bounded Stimulated Reservoir Volume//SPE 167727- MS.– 2014.
- A Finite Horizontal-Well-Conductivity Model for Pressure Transient Analysis in Multiple Fractured Horizontal Wells // Z. Chen, X. Liao, X. Zhao [et all.] /SPE 177230-MS. – 2015.
- Fei Wang, Shicheng Zhang. Production Analysis of MultiStage Hydraulically Fractured Horizontal Wells in Tight Gas Reservoirs//Journal of Geography and Geology. – 2014. – V. 6. – N 4. – Р. 58-67.
- Cinco-Ley H., Samaniego-V. F. Transient Pressure Analysis: Finite Conductivity Fracture Case Versus Damaged Fracture Case//SPE 10179-MS. – 1981.
- A composite model of hydraulic fractured horizontal well with stimulated reservoir volume in tight oil & gas reservoir /Fan Dongyan, Yao Jun, Sun Hai [et all.] // Journal of Natural Gas Science and Engineering. – 2015. – V. 24. – P. 115-123.
- Zhejun Pan, Luke D. Connell. Reservoir Simulation of Free and Adsorbed Gas Production from Shale//Journal of Natural Gas Science and Engineering. – 2015. – V. 22. – Р. 359-370.
- Wang H., Marongiu-Porcu M. Impact of Shale-Gas Apparent Permeability on Production: Combined Effects of Non-Darcy Flow/Gas-Slippage, Desorption, and Geomechanics // SPE173196-PA. – 2015.
- Song B., Economides M.J., Ehlig-Economides C.A. Design of Multiple Transverse Fracture Horizontal Wells in Shale Gas Reservoirs//SPE 140555-MS. – 2011.
- Advances in the Method of production performance prediction of SRV fractured horizontal Wells/Ren Long, Su Yuliang, Xu Chen, Meng Fankun// Acta Geologica Sinica (English Edition). – 2015. – 89(supp.). – P. 319-320.
- Самарский А.А., Вабищевич П.Н. Разностные схемы для неустойчивых задач. М.: Институт прикладной математики имени М.В. Келдыша АН СССР, 1990. – 24 с.
- Agarwal R.G. Real gas pseudo-time: a new function for pressure buildup analysis of MHF gas wells//SPE 8279. – 1979.
Видео:КАК БУРЯТ НЕФТЯНЫЕ СКВАЖИНЫ ?Скачать

Reference
- Qanbari F., Clarkson C.R., Production data analysis of multifractured horizontal wells producing from tight oil reservoirs — Bounded stimulated reservoir volume, SPE , 2014.
- Chen Z., Liao X., Zhao X., Dou X., Huang C., Chen Y.,Guo X., A finite model for pressure transient analysis in multiple fractured horizontal wells, SPE , 2015.
- Fei Wang, Shicheng Zhang, Production analysis of multistage hydraulically fractured horizontal wells in tight gas reservoirs, Journal of Geography and Geology, 2014, no. 4, рр. 58–67.
- H., Samaniego- Transient pressure analysis: Finite conductivity fracture case versus damaged fracture case, SPE , 1981.
- Fan Dongyan, Yao Jun, Sun Hai, Zeng Hui, Wang Wei, A composite model of hydraulic fractured horizontal well with stimulated reservoir volume in tight oil & gas reservoir, Journal of Natural Gas Science and Engineering, 2015, pp. 115–123.
- Zhejun Pan, Connell L.D., Reservoir simulation of free and adsorbed gas production from shale, Journal of Natural Gas Science and Engineering, 2015, pp. 359–370.
- Wang H., & M.,Impact of apparent permeability on production: Combined effects of flow/, desorption, and geomechanics, SPE , 2015.
- Song B., Economides M.J., C.A.,Design of multiple transverse fracture horizontal wells in shale gas reservoirs, SPE , 2011.
- Ren Long, Su Yuliang, Xu Chen, Meng Fankun, Advances in the Method of production performance prediction of SRV fractured horizontal wells, Acta Geologica Sinica (English Edition), pp. 319–320.
- Samarskiy A.A., Vabishchevich P.N., Raznostnye skhemy dlya neustoychivykh zadach (Difference schemes for unstable problems), Moscow: Publ. of Keldysh Institute of Applied Mathematics of RAS, 1990, 24 p.
- Agarwal R.G., Real gas : a new function for pressure buildup analysis of MHF gas wells, SPE 8279, 1979.
Ссылка на статью в русскоязычных источниках:
The reference to this article in English is:
Видео:Технологии строительства ачимовских горизонтальных скважин с МСГРП. Вызовы. Анализ. РешениеСкачать

ГЛАВА 2 — УСТАНОВИВШИЙСЯ ПРИТОК РЕАЛЬНОГО ГАЗА К ГОРИЗОНТАЛЬНОЙ СКВАЖИНЕ ПО ЛИНЕЙНОМУ И НЕЛИНЕЙНОМУ ЗАКОНАМ ФИЛЬТРАЦИИ
СОДЕРЖАНИЕ
1 КРАТКИЙ ОБЗОР ТЕОРЕТИЧЕСКИХ РАБОТ ОБ УСТАНОВИВШЕМСЯ ПРИТОКЕ ЖИДКОСТИ К ГОРИЗОНТАЛЬНЫМ СКВАЖИНАМ. 5
2 УРАВНЕНИЕ И.А. ЧАРНОГО О ПРИТОКЕ ЖИДКОСТИ К ГОРИЗОНТАЛЬНОЙ СКВАЖИНЕ. 7
3 РАСЧЕТ ДЕБИТА ГОРИЗОНТАЛЬНОЙ НЕФТЯНОЙ СКВАЖИНЫ ПО МЕТОДУ ДЖОШИ.. 12
4 ПРИБЛИЖЕННОЕ РЕШЕНИЕ Ю.П. БОРИСОВА ЗАДАЧИ О ПРИТОКЕ НЕФТИ К ГОРИЗОНТАЛЬНОЙ СКВАЖИНЕ. 14
5 УСТАНОВИВШИЙСЯ ПРИТОК ЖИДКОСТИК ГОРИЗОНТАЛЬНЫМ СКВАЖИНАМ В НЕФТЕГАЗОВЫХ ЗАЛЕЖАХ С ПОДОШВЕННОЙ ВОДОЙ.. 15
РАСЧЕТНАЯ ЧАСТЬ. 19
ПРАКТИЧЕСКОЕ ПРИМЕНЕНИ.. 22
СПИСОК ЛИТЕРАТУРЫ.. 27
ВВЕДЕНИЕ.
Работы по повышению эффективности разработки нефтяных залежей горизонтальными и разветвленно-горизонтальными скважинами начаты около 50 лет назад. За последнее время в различных районах СНГ (Башкортостане, Татарстане, Куйбышевской области, Украине, Средней Азии и др.) пробурено более 100 скважин с горизонтальным стволом. В Западной Сибири горизонтальные скважины пробурены на Салымском, Федоровском, Ем-Еговском, Советском, Вахском и др. месторождениях нефти.
В настоящее время горизонтальные скважины бурятся во всех нефтедобывающих странах мира. Однако наибольшее их количество бурится в США. По данным Американского нефтяного института число горизонтальных скважин в США составляло: в 1987 г. — 28, в 1988 г .— 63, в 1989 г. — 128, в 1990г. — 866, в 1991 г .— 1149, в 1992г. — 2000. В 1993 г. было пробурено 366 скважин, в 1994 г. — 385.
Быстро начинает развиваться бурение горизонтальных скважин в Саудовской Аравии и других странах Среднего Востока. Дебиты горизонтальных скважин здесь обычно превышают дебиты вертикальных в 2—10 раз; увеличение нефтеотдачи ожидается на 5—10%. Обычно горизонтальные скважины здесь имеют большой радиус переходного участка; глубина продуктивного песчаного горизонта составляет 1800—2300 м; горизонтальный ствол составляет 480 — 600 м с диаметром 8,5м. В карбонатных породах такая промежуточная колонна спускается на глубину 3000 м, длина горизонтальных стволов в море составляет 730—970 м, а на суше — 600—700 м.
Сотни горизонтальных скважин закончены и эксплуатируются во многих регионах мира: от Франции, Италии и Северного моря до морских скважин Явы и Китая. В связи с бурным ростом бурения скважин с горизонтальным стволом и высокой экономической эффективностью их использования встают такие крупномасштабные задачи, как создание системы раз работки нефтяных месторождений горизонтальными скважинами, совершенствование технологии добычи нефти горизонтальными скважинами, методов воздействия на призабойную зону, методов испытания скважин после бурения и гидродинамического исследования горизонтальных скважин.
В отличие от исследования вертикальных скважин проблема гидродинамических исследований и интерпретация их результатов является более сложной, ввиду неоднозначности характера линий тока, как в области дренирования, так и во времени. Имеющиеся аналитические решения о притоке жидкости и газа к горизонтальным скважинам и несовершенным галереям (трещинам) требуют тщательного их анализа и изучения, чтобы обоснованно использовать то или иное решение в конкретной ситуации.
Для отечественной нефтепромысловой практики имеется «Руководство по гидродинамическим исследованиям наклонных и горизонтальных скважин». В настоящей работе интерпретация результатов исследований несовершенных горизонтальных скважин при установившихся и неустановившихся режимах фильтрации базируется на более эффективных аналитических решениях и новой концепции о характере линий тока в пространстве и во времени.
ЦЕЛЬ И ЗАДАЧИ КУРСОВОЙ РАБОТЫ
Целью данной курсовой работы является изучение притока(дебита) жидкости и газа к горизонтальным скважинам. Горизонтальными называются скважины, в которых интервал вскрытия продуктивного пласта стволом скважины более чем в два раза превышает толщину пласта.
В процессе изучения притока жидкости и газа многие ученые предлагали свои методы и решения по вычислению дебита.
Задачи данной работы следующие:
1) Изучение и анализ уравнения И.А. Чарного о притоке жидкости к горизонтальной скважине.
2) Расчет дебита горизонтальной скважины по методу Джоши.
3) Анализ решения Ю.П. Борисова задачи о притоке.
4) Расчет дебита газа горизонтальной скважины.
5) Анализ установившегося притока реального газа к горизонтальной скважине по нелинейному закону фильтрации.
ГЛАВА 1 — КРАТКИЙ ОБЗОР ТЕОРЕТИЧЕСКИХ РАБОТ ОБ УСТАНОВИВШЕМСЯ ПРИТОКЕ ЖИДКОСТИ К ГОРИЗОНТАЛЬНЫМ СКВАЖИНАМ
1.1 Теоретическая часть
Традиционные методы разработки месторождений системой вертикально пробуренных скважин не всегда эффективны. В 50-е годы в нашей стране группа специалистов начала разрабатывать и применять специальную технику и технологию бурения многозабойных наклонных и горизонтальных скважин. Большой вклад в этом направлении был сделан А.М. Григоряном. В эти же годы были выполнены первые теоретические работы по расчету притока нефти к горизонтальным (П.Я. Полуборинова-Кочина, Ю.П. Борисов, В.П. Пилатовский, В.П. Меркулов, В.П. Табаков). Однако отсутствие необходимой техники в то время не позволило найти широкое практическое применение этому методу.
В последнее десятилетие в нашей стране и за рубежом интенсивные практические и теоретические работы в области применения технологии наклонно горизонтального бурения. Преимущества горизонтальных скважин в ряде случаев очевидны. Горизонтальная скважина имеет значительно большую область дренирования, чем вертикальная. Особенно проявляется этот эффект в пластах малой продуктивной толщины. Область дренирования горизонтальной скважины можно аппроксимировать объемом достаточно протяженного вдоль напластования эллипсоида, тогда как вертикальная скважина дренирует объем кругового цилиндра. Продуктивность горизонтальной скважины растет с ее длиной. Выигрыш в производительности может быть в 3-5 раз.
Горизонтальные скважины особенно эффективны в месторождениях, содержащих вертикальные трещины. В сильно неоднородных по проницаемости пластах (таких, например, как карстовые залежи) горизонтальные скважины имеют большую вероятность встретить продуктивную зону, чем вертикальные. В плане борьбы с обводнением горизонтальная скважина так же имеет преимущества.
Гидродинамические расчеты технологических показателей процесса разработки месторождений горизонтальными и наклонными скважинами не могут быть выполнены при помощи обычных формул, применяемых для расчета взаимодействия вертикальных скважин. Поэтому развитие гидродинамических методов подобных расчетов является в настоящее время актуальной задачей. Приведем здесь идею некоторых приближенных подходов к определению дебита горизонтальной скважины, не останавливаясь на выкладках и преобразованиях.
1.2 Уравнение И.А. Чарного о притоке жидкости к горизонтальной скважине
Вопросам притока к горизонтальным скважинам посвящено большое количество научных работ. При этом весьма ограниченное число работ посвящено горизонтальным газовым и газоконденсатным скважинам и практически не исследованы вопросы притока к пологим нефтяным и газовым скважинам. Одни из первых работ по гидродинамике притока жидкости к горизонтальным скважинам были опубликованы в нашей стране.
И.А. Чарный получил решение притока несжимаемой жидкости к горизонтальному стволу, ассиметрично расположенному относительно контуров питания с расстояниями 
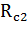


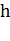

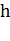
Где: 



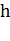

Позднее А.М. Пирвердян изучил аналогичную задачу для случая, когда одна из границ закрыта (непроницаема), например, при 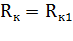

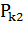
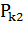
Где: 

В работе В.П. Пилатовского задача решена в более общей постановке для случая, когда скважина расположена несимметрично относительно кровли и подошвы пласта, а на контурах питания заданы разные давления. При условиях 
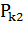

Теоретические исследования И.А. Чарного и А.М. Пирвердяна в посвящены вопросам притока жидкости к горизонтальным скважинам бесконечной длины в пластах конечной толщины. Если использовать эти формулы для определения дебита горизонтальных скважин конечной протяженности, то результат будет заниженным, причем ошибка при разных длинах скважин и толщинах пласта не поддается строгому определению. Кроме того полученные формулы пригодны только для полосообразной залежи. В работах З.С. Алиева и В.В. Шеремета, В.В. Бондаренко предложена формула для определения дебита нефтяной горизонтальной скважины полностью вскрывшей полосообразный фрагмент однородного пласта. По этому методу допускается, что область фильтрации состоит из двух зон, в каждой из которых вблизи ствола толщина пласта считается функцией радиуса, т.е. 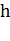

Рисунок 1 — Схема расположения стола горизонтальной скважины по толщине пласта: а) – симметричное; б) – асимметричное.
Уравнение для определения дебита нефти согласно работе З.С. Алиева и др. имеет вид[3]:
В случае, если ствол горизонтальной скважины расположен асимметрично по толщине, то дебит скважины будет определяться суммой дебитов из верхней и нижней зон, (см. рисунок 1,б)[1] по формуле[3]:
Где: 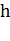


Для анизотропного пласта дебит горизонтальной нефтяной скважины определяется по формуле[3]:
Где: 

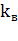
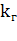
В данном случае учет влияния параметра анизотропии осуществлен по формуле, полученной для изотропного пласта путем уменьшения толщины пласта на величину 

Если ствол скважины перемещен относительно центра зоны дренирования на расстояние « 
Где: 
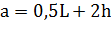






1.3 Расчет дебита горизонтальной нефтяной скважины по методу Джоши
Преимущества скважин с горизонтальным стволом наилучшим образом можно понять путем простого анализа работы скважины. Поведение горизонтальной скважины анализируется, когда приток пластовой жидкости происходит по всей длине горизонтального ствола в продуктивном пласте, что отвечает открытому стволу, с хвостовиком, имеющим щелевидные отверстия, или перфорированной колонне с достаточно высокой плотностью, что позволяет не учитывать добавочные фильтрационные сопротивления за счет перфорации, а также скин-эффект, обусловленный загрязнением призабойной зоны. Для выполнения более надежных сравнений необходимо рассматривать как переходный, так и псевдостационарный процессы фильтрации. Это особенно важно для низкопроницаемых коллекторов, в которых продолжительность переходного режима фильтрации очень высока. Однако для достаточно больших периодов работы скважин вполне приемлемо рассмотреть псевдостационарный процесс фильтрации. Приток к горизонтальному стволу скважины, в зависимости от его длины, можно рассчитать по формуле Джоши[1]:



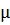
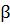

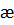



Формула (9) может быть использована как для расчета дебита, так и для оценки «кратности увеличения» дебита (отношения коэффициентов продуктивности) при сравнении производительности скважин с горизонтальным и вертикальным стволами, законченными на один и тот же пласт.
Для расчета дебита горизонтальной скважины, расположенной в центре расчетного блока, авторами предлагается использовать следующую формулу[1]:



1.4 Приближенное решение Ю.П. Борисова задачи о притоке нефти к горизонтальной скважине
Рассматривается установившийся приток к одиночной горизонтальной скважине длиной 
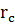

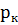
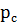
Рисунок 2 — Схема горизонтальной скважины с круговым контуром питания.
Полное фильтрационное сопротивление можно представить суммой двух сопротивлений: внешнего — от контура питания до прямолинейной вертикальной галереи, совпадающей с проекциями горизонтальной скважины на кровлю (или подошву) пласта, и внутреннего, обусловленного тем, что мы имеем в действительности не галерею, а скважину. Внешнее сопротивление определяется по формуле[1]:

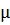
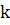


Внутреннее сопротивление определяется так же, как и для одной вертикальной скважины в батарее. Приняв толщину рассматриваемого пласта, соответствующей расстоянию между скважинами, а длину ствола горизонтальной скважины, равной толщине в случае вертикальной скважины, имеем[1]:
Где: 
Эту же формулу можно получить, мысленно разрезав горизонтальную скважину на отрезки длиной, равной толщине пласта 


Сумма указанных сопротивлений дает отношение перепада давления к дебиту горизонтальной скважины :



ГЛАВА 2 — УСТАНОВИВШИЙСЯ ПРИТОК РЕАЛЬНОГО ГАЗА К ГОРИЗОНТАЛЬНОЙ СКВАЖИНЕ ПО ЛИНЕЙНОМУ И НЕЛИНЕЙНОМУ ЗАКОНАМ ФИЛЬТРАЦИИ
Видео:Горизонтально направленное бурение| Технология ГНБ| Как это работает?Скачать

Уравнения притока жидкости к скважине.
Приток жидкости в скважины происходит под действием разницы между пластовым давлением и давлением на забое скважины. При постоянной толщине пласта и открытом забое скважины жидкость движется к забою по радиально-сходящимся направлениям. В таком случае говорят о плоскорадиальной форме потока.
Если скважина достаточно продолжительно работает при постоянном забойном давлении, то скорость фильтрации и давление во всех точках пласта перестает изменяться во времени и поток является установившемся.
Для установившегося плоскорадиального потока однородной жидкости дебит скважины можно определить по формуле:
где,
Q – дебит скважины [л/с], [м 3 /сут], [т/сут] и.т.п. (объем жидкости, поступающий на забой скважины в единицу времени);
k – проницаемость пласта [мкм 2 ](микрометр) 1 мкм 2 = 1 Д = 10 -12 м 2 ;
h – толщина пласта [м];
pк – пластовое давление [Па];
pз – забойное давление в скважине [Па];
μ – вязкость жидкости [Па*с];
Rк – радиус контура питания [м];
rс – радиус контура скважины [м].
Формула, называемая формулой Дюпюи, широко используется для расчета дебита гидродинамически совершенных скважин.
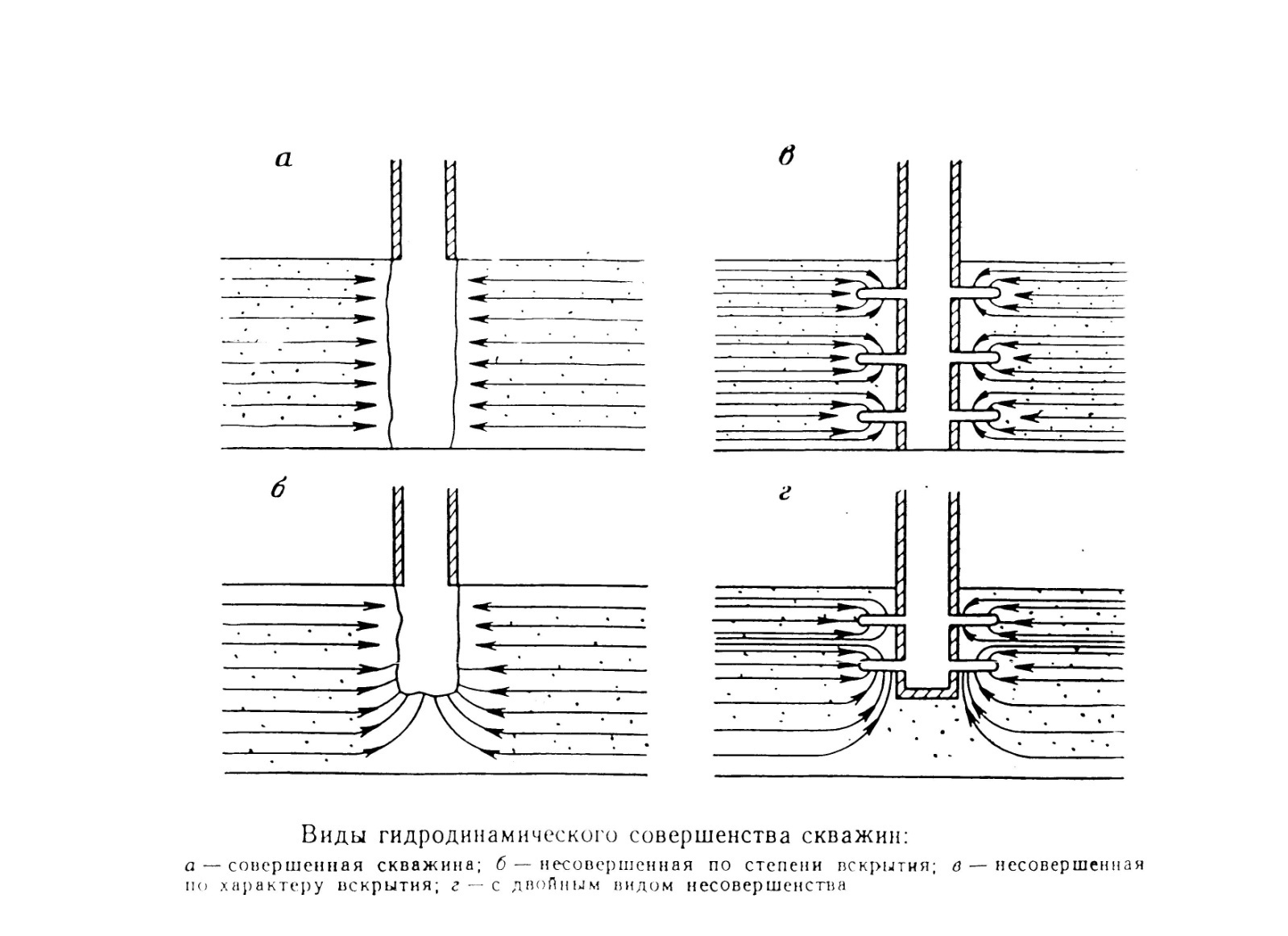
К гидродинамически совершенным скважинам (ГДС) относят скважины с открытым забоем, вскрывшие пласты на всю толщину (рис. а).
Если скважина имеет открытый забой, но вскрыла пласт не на всю толщину, то ее называют гидродинамически несовершенной по степени вскрытия (рис. б).
Скважины, вскрывшие пласт на всю толщину, но соединяющиеся с пластом посредством перфорации, являются гидродинамически несовершенными по характеру вскрытия (рис. в) .
Есть скважины и с двойным видом несовершенства – как по степени, так и по характеру вскрытия (рис. г).
Вблизи ствола гидродинамический несовершенной скважины происходит искажение плоскорадиальной формы потока и возникают дополнительные фильтрационные сопротивления потоку жидкости.
При расчете дебита скважин их гидродинамическое несовершенство учитывается введением в формулу Дюпюи коэффициента дополнительных фильтрационных сопротивлений С.
Величина коэффициента дополнительных фильтрационных сопротивлений зависит от степени вскрытия пласта, плотности перфорации и диаметра перфорационных каналов. Обычно ее определяют, используя графики И.В. Щурова.
Основные понятия о разработке нефтяных и газовых месторождений. Пластовая энергия и силы, действующие в залежи. Природные режимы работы нефтяных и газовых залежей.
Одной из главных целей разработки месторождения является извлечение максимального количества нефти из недр.
Разработка нефтяных и газовых месторождений – это комплекс мероприятий, направленных на обеспечение притока нефти и газа из залежи к забою скважин, предусматривающих с этой целью определенный порядок размещения скважин на площади, очередность их бурения и ввода в эксплуатацию, установление и поддержание определенного режима их работы.
Под режимом работы нефтяных и газовых залежей понимают характер проявления движущих сил, обеспечивающих продвижение нефти в пластах к забоям эксплуатационных скважин.
Залегающие в пластах нефть и газ находятся под действием сил, совокупность которых обусловливает движение нефти, газа и воды в пластах при их разработке, а также характер и интенсивность этого движения.
Силы, действующие в пласте, можно разделить на две группы: силы движения и силы сопротивления, противодействующие движению жидкостей и газа и удерживающие нефть в пластах.
К силам, обусловливающим движение нефти, газа и воды в пластах, относятся следующие:
- силы, вызываемые напором пластовых контурных вод;
- силы, вызываемые напором свободного газа, заключенного в газовой шапке;
- силы, вызываемые расширением сжатого газа, растворенного в нефти;
- силы, проявляющиеся в результате упругости пластовых водонапорных систем, т.е. упругости жидкости и собственно пород пластов;
- сила тяжести нефти.
В процессе движения нефти и газа в пласте чаще всего действуют различные виды энергии одновременно. Так, всегда проявляются упругость пород и жидкостей и сила тяжести. Однако в зависимости от геологических условий и условий эксплуатации месторождения превалирует энергия того или иного вида.
К силам сопротивления движения нефти в пласте относятся:
- внутреннее трение жидкости и газа, связанное с преодолением их вязкости;
- трение нефти, воды или газа о стенки поровых каналов нефтегазосодержащей породы;
- межфазное трение при относительном движении жидкости и газа по пласту;
- капиллярные и молекулярно-поверхностные силы, удерживающие нефть в пласте благодаря смачиванию ею стенок поровых каналов.
Гидравлическое сопротивление движению жидкости и газа по пласту зависит прежде всего от вязкости движущихся жидкостей и газа и от скорости потока. Чем выше скорость потока и выше вязкость, тем больше силы сопротивления.
Виды режимов работы нефтяных и газовых залежей:
— водонапорный (жестководонапорный) режим (рис. а) источником энергии является напор краевых (или подошвенных) вод. Ее запасы постоянно пополняются за счет атмосферных осадков и источников поверхностных водоемов. Отличительной особенностью этого режима является то, что поступающая в пласт вода полностью замещает отбираемую нефть. Контур нефтеносности при этом непрерывно перемещается и сокращается.
Эксплуатация нефтяных скважин прекращается, когда краевые воды достигают забоя тех из них, которые находятся в наиболее высоких частях пласта, и вместо нефти начинает добываться только вода.
При водонапорном режиме давление в пласте настолько велико, что скважины фонтанируют. Но отбор нефти и газа не следует производить слишком быстро, поскольку иначе темп притока воды будет отставать от темпа отбора нефти и давление в пласте будет падать, фонтанирование прекратиться. Коэффициент нефтеотдачи пласта при данном режиме – 0,5…0,8
Коэффициент нефтеотдачи пласта — это доля извлеченной из пласта нефти от ее первоначальных запасов.
— газонапорный режим (или режим газовой шапки)(рис. б) источником энергии для вытеснения нефти является давление газа, сжатого в газовой шапке. Газ, действуя на поверхность газонефтяного контакта, создает давление в нефти, заполняющей поры продуктивного пласта. Чем больше размер газовой шапки, тем дольше снижается давление в ней. Коэффициент нефтеотдачи пласта – 0,5…0,6.
— режим растворенного газа (газовый) (рис. в) основным источником пластовой энергии является давление газа, растворенного в нефти. По мере понижения пластового давления газ из растворенного состояния переходит в свободное. Расширяясь пузырьки газа выталкивают нефть к забоям скважин. Коэффициент нефтеотдачи – самый низкий 0,2…0,4. Причина этого в том, что запас энергии газа часто полностью истощается намного раньше, чем успевают отобрать значительные объемы нефти.
— упруговодонапорный (упругий) режим основным источником пластовой энергии служат упругие силы воды, нефти и самих пород, сжатых в недрах под действием горного давления. Коэффициент нефтеотдачи пласта – может достигать 0,8.
— гравитационный режим (рис. г) проявляется тогда, когда давление в пласте упало до минимума, напор контурных вод отсутствует, газовая энергия полностью истощена. При этом режиме нефть стекает в скважину под действием силы тяжести, а оттуда она откачивается механизированным способом. Коэффициент нефтеотдачи пласта – 0,1 – 0,2.
— смешанный режим — если в нефтяной залежи одновременно действуют различные движущие силы.
При разработке газовых месторождений гравитационный режим и режим растворенного газа отсутствуют.
Естественная пластовая энергия в большинстве случаев не обеспечивает высоких темпов и достаточной полноты отбора нефти из залежи. Это связано с тем, что ее извлечению из пласта препятствует достаточно много факторов, в частности, силы трения, силы поверхностного натяжения и капиллярные силы.
💥 Видео
Очистка ствола при бурении наклонных и горизонтальных скважин. Бурение с большим отходом.Скачать

освоение скважинСкачать

Бурение горизонтальных скважин. Часть 1.Скачать

Применение горизонтальных скважин на Ямсовейском месторожденииСкачать

Горизонтальная скважина. TMK UP CENTUM.Скачать

Система разработки горизонтальных скважинСкачать

В–О. №18 «Как рассчитать скин-фактор согласно степени вскрытия пласта и оценить изменение Коэф. про»Скачать

Учебный фильм Геофизические исследования скважинСкачать