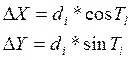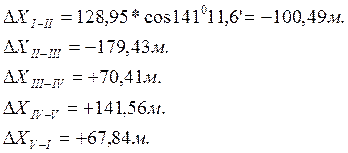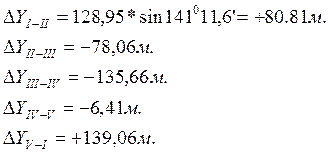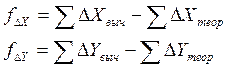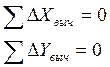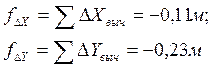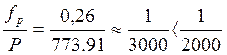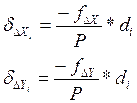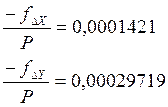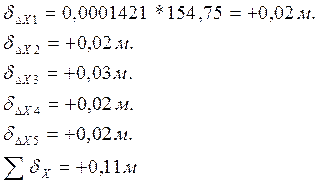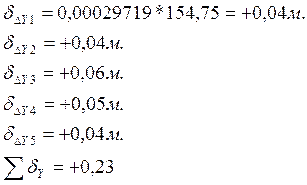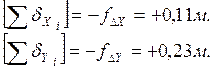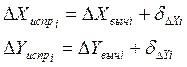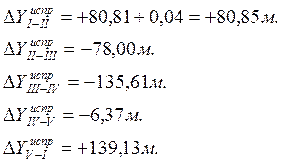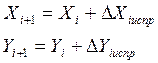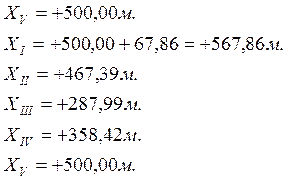Страницы работы
Содержание работы
Вычисление координат вершин замкнутого хода
Измеренные правые по ходу горизонтальные углы
Горизонтальные проложения длин сторон, м.





- Вычисление исправленных горизонтальных углов:
Угловая невязка в замкнутом ходе определяется по формуле:
где 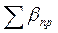
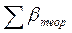
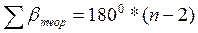
Допустимая угловая невязка в замкнутом ходе определяется по формуле:
Условие 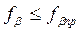
Контроль вычисления поправок
Правые по ходу исправленные горизонтальные углы
Проверка правильности вычислений:
- Вычисление дирекционных углов всех сторон хода по исправленным горизонтальным углам:
Дирекционный угол Т-это угол, отсчитываемый от положительного (северного) направления осевого меридиана до данного направления по ходу часовой стрелки. Он измеряется от 0 0 до 360 0 .
Исходный дирекционный задан 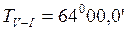
Где Тn+1-дирекционный угол последующей стороны; Тn— дирекционный угол предыдущей стороны; 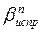
Контролем правильности вычислений служит равенство вычисленного значения дирекционного угла исходной стороны его заданному значению.
- Вычисление приращения координат
и
по дирекционным углам и горизонтальным проложениям сторон теодолитного хода:
Приращение координат ∆X и ∆Y по дирекционным углам и горизонтальным проложениям сторон теодолитного хода определяется по формулам:
где di— горизонтальное проложение стороны хода; Ti-дирекционный угол, соответствующие данному направлению.
- Вычисление поправок к приращениям:
Невязки приращения координат – это разности их вычисленного и теоретического значения
Так как ход замкнут, то теоретические суммы приращений координат
и невязки приращения координат равны вычисленным суммам приращений координат:
Абсолютная невязка: 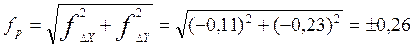
Относительная невязка удовлетворяет указанному допуску, следовательно 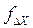
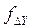
где 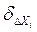
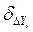
Проверка:
- Вычисление исправленных приращений:
Исправленные значения приращений координат для каждой линии вычисляется по формуле:
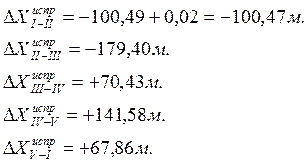
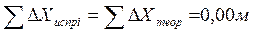
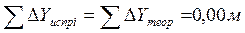
- Вычисление координат вершин замкнутого хода:
Координаты X и Y вершин замкнутого хода определяются по формулам:
Контролем правильности вычислений служит получение значений координат конечного исходного пункта X1 и Y1 (он же — начальный пункт).
Видео:5. Увязка приращений координат. Часть 1Скачать

· Накладка вершин углов теодолитного хода на план:
Накладка теодолитного хода по координатам вершин на план в масштабе 1:2000 начинается с построения координатной сетки. Для её построения применяются линейки Дробышева. Это металлическая линейка с вырезами. Края вырезов скошены, на первом из них нанесён индекс «0». Края других вырезов представляют дуги, описанные радиусами 10, 20, 30, 40, и 50 см; конец линейки представляет также дугу радиусом 70, 711 см, что соответствует гипотенузе треугольника с катетами 50х50 см.
На листе бумаги проводим диагонали, от точки пересечения откладывают равные отрезки к углам листа, получая таким образом вершины прямоугольника. Затем по сторонам прямоугольника откладывают отрезки(10 см), величину которых определяют по масштабу. Соответствующие точки на противоположных сторонах соединяют линиями, которые образуют сетку квадратов. Контролируют построения по равенству диагоналей в каждом квадрате. Расхождение диагоналей не должно превышать 0,2 мм. Затем полученная сетка квадратов оцифровывается так, чтобы весь ход оказался примерно в середине листа, при этом +Х направляется вверх листа, а +У – вправо.
При нанесении на план точек по прямоугольным координатам прежде всего определяют квадрат, в котором они находятся. Построение производят с помощью циркуля-измерителя и масштабной линейки. Каждую точку накладывают и обвожу кружком диаметром 1,5 мм с «усиками» длиной 0,5 мм, слева подписывают номера вершин. Правильность накладки проверяют, сравнивая расстояния между точками с горизонтальным положением сторон в масштабе плана. Допустимое расхождение ±0,6 мм.
Работу оформляют карандашом в соответствии с образцом и условными знаками.
Видео:4. Вычисление приращений координатСкачать

Вычисление и уравнивание приращений координат
Вычисление приращений координат и их уравнивание это первый этап решения прямой геодезической задачи. Для вычисления приращения координат линии теодолитного хода необходимо знать горизонтальное проложение этой линии и её направление, то есть дирекционный угол.
Результаты измерения длин линий в прямом и обратном направлениях приведены на схеме (рис.1). В скобках, на чертеже даны углы наклона к горизонту для соответствующих линий. Горизонтальные проложения находятся, как среднее арифметическое из двух значений с учётом поправки за наклон линии к горизонту. Введение поправки требуется, если угол наклона более 1,5º.
Направление исходной стороны определено в разделе 2. Дирекционный угол последующей стороны полигона равен дирекционному углу предыдущей стороны плюс 180º и минус исправленный правый угол при вершине. Вычисления производятся в виде непрерывного столбца:
В результате вычислений по замкнутому контуру должно получиться точное значение исходного направления. Если условие контроля выполнено, то полученные значения дирекционных углов выписываются в Ведомость (приложение , столбец 4).
Для каждой линии теодолитного хода, с помощью калькулятора вычисляются приращения координат. При работе с калькулятором следует помнить, что аргумент тригонометрической функции должен быть в градусах и десятичной форме.
Например, требуется найти значение cos(113º 54,6′).
Для этого выполняются следующие действия:
54,6/60 +113 = функция cos результат -0,40530.
∆X2 = 26,76 * cos(113º54,6′) = 10,85 м,
∆Y2 = 26,76 * sin(113º54,6′) = 24,46 м.
Теоретическая сумма приращений координат по Х и по Y равна нулю так, как теодолитный ход замкнутая фигура. Фактические суммы приращений координат замкнутого полигона могут отличаться от нуля и их величины принято называть невязками.
Абсолютная невязка полигона
Отношение абсолютной невязки к периметру полигона называется относительной невязкой
Относительная невязка не должна превышать предельного значения<fотн>, в зависимости от условий на местности.
В случае, если относительная невязка допустима, то следует выполнить уравнивание приращений координат путём введения поправок. Поправки вводятся пропорционально длинам линий с точностью до сантиметра. Сумма поправок должна быть равна невязке с обратным знаком по соответствующей координате. Исправленные приращения координат выписываются в ведомости под соответствующими вычисленными ранее значениями.
Вычисление координат
Координаты исходного пункта теодолитного хода получены в разделе 2. Координаты последующих пунктов хода вычисляются через исправленные приращения в виде:
т.2 713,75 1023,52
Контроль вычислений состоит в получении значений координат исходного пункта. По завершении контроля вычислений, значения координат всех пунктов выписываются в Ведомость.
Составление плана
6.1 Построение координатной сетки
Координатная сетка на чистом листе ватмана произвольной формы может быть построена различными способами. Например, с помощью линейки Ф.В. Дробышева, способом диагоналей или путём использования просветного экрана.
В результате построений должна быть получена сетка правильных квадратов, в количестве достаточном для изображения всех вершин полигона и пунктов опорной геодезической сети.
В первую очередь на чистом листе необходимо построить прямоугольник максимально возможного размера. При построении будем использовать известное из геометрии свойство диагоналей прямоугольника – они равны между собой и в точке пересечения делятся пополам. Таким образом, если от точки пересечения диагоналей отложить равные отрезки на самих диагоналях, то это будут вершины прямоугольника. Последовательно соединим эти вершины и получим исходную фигуру для ориентирования координатных линий.
Координатные линии на всех топографических планах проводятся с одинаковым шагом, равным 100 мм.
При необходимости сетка квадратов может быть сдвинута относительно центра листа. Это целесообразно в том случае, когда возникает необходимость «центрировать» полигон в целях экономии бумаги. Если «центрирование» не требуется, то исходные координатные линии могут быть проведены через точку пересечения диагоналей. Все прочие координатные линии строятся от исходных с шагом 100 мм. Для обеспечения требуемой точности построений каждая координатная линия должна проводиться через две точки. Эти точки отмечаются на противоположных сторонах прямоугольника.
Готовые квадраты контролируются с помощью циркуля – измерителя путём сравнения диагоналей. Точность построения каждого из квадратов должна находиться в пределах +/- 0,2 мм.
Оцифровка линий координатной сетки производится таким образом, что бы расположение полигона было оптимальным. Все надписи должны быть кратными шагу линий на местности, который определяется исходя из заданного масштаба. Например, для масштаба 1:500 шаг координатных линий 50 метров. Все надписи в этом случае должны быть кратными 50 метрам. Следует помнить, что в геодезии принята левая система координат, поэтому ось «Х» направлена снизу вверх, а ось «У» слева на право.
6.2 Нанесение пунктов хода на план.
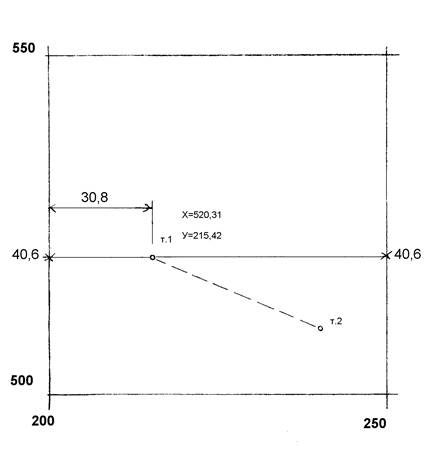
По координатам отдельного пункта определяется квадрат сетки, которому он принадлежит. Пусть это будет т.1 с координатами Х=520,31 м и У=215,42 м. Требуемый квадрат изображен на чертеже (см. рис. 2 ).
Рис. 2 Схема графических построений.
От ближайшей координатной линии Х=500 м, отложим 20,31 м. В масштабе плана, на бумаге это будет 40,6 мм. Откладывать следует вдоль У=200 и У=250. Соединим полученные точки. Это будет линия с абсциссой Х=520,31м. От точки пересечения этой линии с координатной линией У=200 м отложим горизонтальный отрезок 30,8 мм, соответствующий на местности 15,42 м. Полученное положение т.1 можно будет считать окончательным только после проведения контрольных действий. Контроль сводится к проверке инварианта положения, то есть длины некоторого отрезка, к одному из концов которого принадлежит данная точка. Нанесём на план последующую вершину т.2 и измерим на бумаге горизонтальное проложение между этими пунктами. По ведомости координат находим фактическое значение и сравниваем его с измеренным.
Допускаемое расхождение +/- 0,5 мм в масштабе плана.
По окончании контроля положения всех пунктов хода, производится их закрепление с помощью иглы циркуля и условного знака. Пункт теодолитного хода, временного закрепления на местности вычерчивается на плане под лекало в виде окружности диаметром 1,5 мм.
6.3 Графическое оформление.
Для графического оформления чертежа плана, выбранного масштаба имеются общепринятые правила[ 3 ].
Стандартный формат масштабного изображения – 500 на 500 мм. Это сетка из 25 квадратов (5на 5) размером 100 на 100 мм. По периметру поля чертежа проводится внешняя, оформительская рамка толщиной линии 1,2 мм. Расстояние между внешней и внутренней рамками постоянное и равно 12,8 мм.
Координатные линии полностью не изображаются, а представляются в виде перекрестий размером 6 на 6 мм, линиями зелёного цвета. Помимо перекрестий показываются выходы координатных линий на линии рамки в виде штрихов по 3 мм.
Пример рамок и внешнего оформления с указанием шрифтов надписей можно найти в справочнике [ 3, табл. 120].
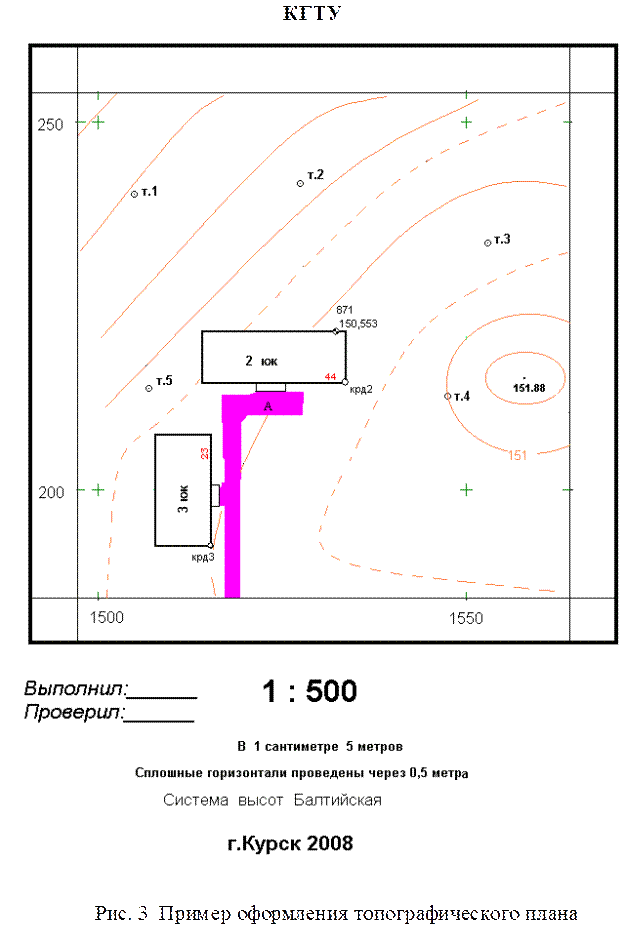
Иногда используют нестандартный формат, в зависимости от размера изображения. При оформлении топографического плана, в любом случае, следует использовать стандартные условные знаки. Пример графического оформления приведен на рис 3.
1. . Инженерная геодезия [Текст]: учебник под ред. Д.Ш. Михелёва М. , 2001.
2. . Практикум по инженерной геодезии[Текст]: Б.Б. Данилевич, В.Ф. Лукьянов, Б.С. Хейфец [и др.], М., 1987.
3. Условные знаки для топографических планов масштабов 1:5000, 1:2000, 1:1000, 1:500[Текст]: М. 2000.
Ведомость вычисления координат пунктов теодолитного хода
Видео:геодезия , ведомость выч. коорд. (приращение коорд.) 1 частьСкачать

Уравнение приращений координат
Контрольная работа № 1
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ И ПОСТРОЕНИЕ
ПЛАНА ТЕОДОЛИТНОЙ СЪЕМКИ
Задание
Цель работы – освоение методики обработки результатов полевых измерений и составление плана местности теодолитной съемки.
Исходные данные.
αА-I = 284°45,5¢; αIV-В = 75°15,5¢; xI = 6240,24м; yI = 4384,33м;
xIV = 6454,57 м; yIV = 4594,01 м.
I = 100º01,0´; II = 162º17,3´; III = 81º15,3´; IV = 225º58,0´.
Ведомость измерения длин линий теодолитного хода
| Линия | Длина линии | Угол наклона |
| I-II | 120,65 | 2º50´ |
| II-III | 136,18 | 2º55´ |
| 50,41 | 6º20´ | |
| III-IV | 104,12 | 2º45´ |
| 46,43 | 5º40´ |
Измеренные превышения между точками теодолитно-высотного хода
| Линия | Превышение h, м |
| I-II | +4,80 |
| II-III | -1,20 |
| III-IV | -0,30 |
Вычисление координат вершин теодолитного хода.
Уравнение измеренных горизонтальных углов.
Для угловой невязки:
Fβ = ∑βизм — ∑βтеор (1)
где ∑βизм – сумма измеренных горизонтальных углов в ходе;
∑βтеор – теоретическое значение суммы измеренных горизонтальных углов в ходе.
Для разомкнутого теодолитного хода:
f βтеор = 180º * n + αнач — αкон (2)
где αнач – дирекционный угол начального направления;
αкон – дирекционный угол конечного направления;
n – число измеренных углов хода.
Тогда: fβ = ∑βизм — 180º * n + αнач — αкон. (3)
Ведомость вычислений координат точек теодолитного хода
| Номе ра точек | Углы | Длины сторон | Приращения координат | Координаты | Номе ра точек | ||
| Измерен ные | Исправ ленные | Дирек ционные | вычесленные | исправленные | x | y | |
| Δx | Δy | Δx´ | Δy´ | ||||
| А | А | ||||||
| -0,4´ | 284º45,5´ | ||||||
| I | 100º01,0´ | 100º00,6´ | +0,02 | +0,04 | 6240,24 | 4384,33 | I |
| -0,4´ | 4º44,9´ | 120,50 | +120,14 | +10,00 | +120,16 | +10,04 | |
| II | 162º17,3´ | 162º16,9´ | +0,04 | +0,07 | 6360,40 | 4394,37 | II |
| -0,4´ | 22º28,0´ | 186,09 | +171,95 | +71,09 | +171,99 | +71,16 | |
| III | 81º15,3´ | 81º14,9´ | +0,03 | +0,06 | 6532,39 | 4465,53 | III |
| -0,4´ | 121º13,1´ | 150,20 | -77,85 | +128,42 | -77,82 | +128,48 | |
| IV | 225º58,0´ | 225º57,6´ | 6454,57 | 4594,01 | IV | ||
| 75º15,8´ | ∑Δx= =+214,24 | ∑Δy= =+209,51 | |||||
| B | B |
∑βизм = 569º31,6´ P = ∑d = 456,79м fx = 214,24 — (6454,57 -6240,24) = -0,09 м
fβ =∑βизм — 180º * n + (αкон +360 º — αнач) = fy = 209,51 — (4594,01 -4384,33) = -0,17 м
= 569º31,6´- 720º + 150 º 30´ = +1,60´ fабс = √(-0,09)² +(-0,17)² = 0,19 м
fотн = 0,19/456,79 = 0,000416
Вычисление дирекционных углов сторон теодолитного хода.
Значение дирекционного угла начального направления αА-I нам дано.
Дирекционные углы последующих сторон хода вычисляют по формуле:
αi = αi-1 + 180º — βi испр, (8)
где αi, αi-1 – дирекционные углы соответственно последующей и предыдущей сторон хода;
βi испр – соответствующий исправленный горизонтальный угол.
αI-II = αА-I + 180º — βI испр = 284º45,5´ — 180º — 100º00,6´ = 4º44,9´
αII-III = αI-II + 180º — βII испр = 4º44,9´ + 180º — 162º16,9´ = 22º28,0´
αIII-IV = αII-III + 180º — βIII испр = 22º28,0´ + 180º — 81º14,9´ = 121º13,1´
αIV-B = αIII-IV + 180º — βIV испр = 121º13,1´ + 180º — 225º57,3´ = 75º15,8´
Вычисление горизонтальных проложений сторон теодолитного хода.
Горизонтальные проложения линий находят по формуле:
где L – измеренная на местности длина линии;
v – угол наклона линии.
dI-II = 120,65 * cos2º50´ = 120,50 м
d1 = 136,18 * cos2º55´ = 136,00 м
d2 = 50,41 * cos6º20´ = 50,09 м
dII-III = d1+ d2 = 186,09 м
d1 = 104,12 * cos2º45´ = 104,00 м
d2 = 46,43 * cos5º40´ = 46,20 м
dIII-IV = d1+ d2 = 150,20 м
Вычисление горизонтальных проложений Таблица 2
| Линия | Длина линии | Угол наклона | Горизонтальное проложение |
| I-II | 120,65 | 2º50´ | 120,50 |
| II-III | 136,18 + 50,41 186,59 | 2º55´ 6º20´ | 136,00 + 50,09 186,09 |
| III-IV | 104,12 + 46,43 150,55 | 2º45´ 6º40´ | 104,00 + 46,20 150,20 |
Суммируя горизонтальные проложения всех сторон хода, находим длину хода (периметр) Р.
Вычисление приращений координат.
Приращения координат вычисляют по формулам:
Δx = d * cosα; Δy = d * sinα, (10)
где d – горизонтальное проложение стороны хода;
α – дирекционный угол стороны хода.
ΔxI-II = 120,50 * cos4º44,9´ = 120,14 м
ΔyI-II = 120,50 * sin4º44,9´ = 10,0 м
ΔxII-III = 186,09 * cos22º28,0´ = 171,95 м
ΔyII-III = 186,09 * sin22º28,0´ = 71,09 м
ΔxIII-IV = 150,20 * cos121º13,1´ = -77,85 м
ΔyIII-IV = 150,20 * sin 121º13,1´ = 128,42 м
Уравнение приращений координат.
Вычислив приращения координат, находим невязки по соответствующим осям:
fx = ∑ Δx — (xкон — xнач),
fy = ∑ Δy — (yкон — yнач), (11)
где ∑ Δx – сумма всех вычисленных приращений Δx;
∑ Δy — сумма всех вычисленных приращений Δy;
xнач, yнач – координаты начальной точки теодолитного хода (точка I);
xкон, yкон – координаты конечной точки теодолитного хода (точка IV).
fx = 214,24 — (6454,57 – 6240,24) = -0,09 м
fy = 209,51 — (4594,01 – 4384,33) = -0,17 м
Для определения допустимости указанных невязок вычисляем абсолютную невязку теодолитного хода по формуле:
🎦 Видео
Вычисление координат точек теодолитного ходаСкачать

3 Теодолитная съемка. Продолжение обработки ведомости вычисления координат. Приращения.Скачать

Теодолитный ходСкачать

8. Заполнение ведомости координат замкнутого теодолитного ходаСкачать

Определение приращений координатСкачать

Видеоурок "Преобразование координат"Скачать

Замкнутый теодолитный ход. Заполнение ведомости вычисления прямоугольных координатСкачать

Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

6. Увязка приращений координат. Часть 2Скачать

4. Обработка ведомости координат диагонального (разомкнутого) ходаСкачать

2 Теодолитная съемка. Обработка ведомости вычисления координат. Вычисление дирекционных угловСкачать

Вычисление медианы, высоты и угла по координатам вершинСкачать

9 класс, 6 урок, Уравнение окружностиСкачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Приращение функцииСкачать
6) 5.11.13 Д-14 Расчёт приращенийСкачать








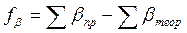
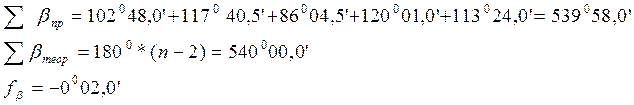
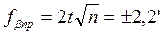
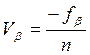
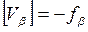
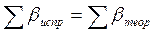
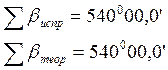
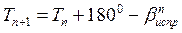
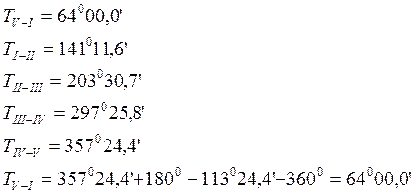
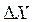 и
и 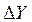 по дирекционным углам и горизонтальным проложениям сторон теодолитного хода:
по дирекционным углам и горизонтальным проложениям сторон теодолитного хода: