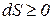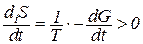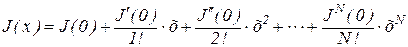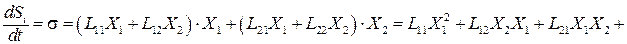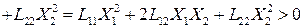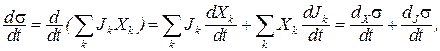Термодинамика – наука, изучающая наиболее общие законы превращения различных видов энергии в системе. Различают:
- термодинамику равновесных систем (классическую, равновесную)
- термодинамику неравновесных систем (линейную и нелинейную).
Под термодинамической системой понимают часть пространства, ограниченную (условно) поверхностью (оболочкой). При этом размеры частиц, составляющих систему (m), должны быть существенно меньше самой системы (М): m 23 Дж·К -1 , а W = N! / N1!·N2!·Nn! – термодинамическая вероятность, причем N = N1 + N2 + ..+ Nn – число вероятных состояний системы.
Таким образом, первый закон термодинамики определяет энергетический баланс в закрытой системе, а второй – дает возможность установить направленность термодинамического процесса.
- Термодинамические потенциалы
- Теорема Пригожина
- Следствие теоремы Пригожина
- Неравновесная термодинамика
- Стационарное состояние живого организма
- Стационарное состояние живого организма
- Стационарное состояние и термодинамическое равновесие
- Уравнение Пригожина
- Основные понятия и особенности кинетики биологических процессов
- Стационарные неравновесные состояния. Термодинамика биологических процессов
- Стационарное состояние. Теорема Пригожина
- Термодинамика биологических процессов
- 🎬 Видео
Термодинамические потенциалы
По изменению δU и δS нельзя оценить величину производимой работы, их начальных и конечных значений. Для этого и вводят термодинамические потенциалы, которые выводятся из объединенной записи первого и второго законов термодинамики.
Объединённая запись первого и второго законов термодинамики:
δQ = TdS ,
TdS = dU + δW ,
dU = δW — TdS.
Видно, что изменение внутренней энергии складывается из двух компонентов:
- δW – совершаемая работа – это свободная энергия,
- TdS – рассеянная в виде тепла – связанная энергия.
Для количественной оценки свободной энергии необходимо наложить ограничения:
- При постоянном давлении (P) работа по изменению объёма будет равна PdV , а количество теплоты, согласно первому закону термодинамики:
Q = ΔU + PΔV = Δ(U + PV ) = ΔH
будет отражать изменение энтальпии – теплосодержание системы.
dH = dU + PdV
H = U + PV
Т.е. энтальпия равна количеству теплоты, выделяемой системой.
Зная энтальпию исходных веществ и продуктов реакции и основываясь на законе Гесса, можно определить её тепловой эффект (см. выше).
При постоянных V и T рассчитывается свободная энергия Гельмгольца.
Совершаемая работа условно состоит из 2 компонент:
W = WΠ + PΔV
TdS = dU + δWΠ + PdV
-δWΠ = dU + PdV — TdS
WΠ– полезная работа, так как PΔV = 0: -δWΠ = dU — TdS = dF – свободная энергия Гельмгольца.
F = U — TS
dF = dU — TdS
При постоянных P и T рассчитывается свободная энергия Гиббса: -δWΠ = dU + PdV — TdS = dH — TdS = dG – свободная энергия Гиббса, и она равна:
G = H — TS ,
dG = dH — TdS ,
Так как в биологических системах p=const., чаще используют энергию Гиббса.
Следствия первого и второго законов термодинамики
- Необратимый процесс всегда сопровождается рассеянием энергии в тепло TdS .
- Если dF 0 и dG > 0 , то процесс несамопроизвольный и обратимый.
- При достижении равновесия F и G —> min., а dF и dG = 0
Для идеального газа с учетом того, что свободная энергия Гиббса при полном дифференцировании: dG = dU + pdV + VdP – TdS – SdT = VdP-SdT, где: dG = VdP-SdT
и постоянной температуре, получим:
Если первое состояние – в стандартных условиях и имеет стандартную величину G 0 , то итоговое значение свободной энергии Гиббса будет равно:
Для разбавленных растворов P ≈ C (концентрация) и тогда:
Для простого процесса A↔B в состоянии равновесия ΔG = 0 , тогда,
а так как B/A = KP (константа равновесия), получаем:
ΔG 0 = -RT lnKP – закон Вант – Гоффа
(ΔG 0 – изменение ΔG при протекании процесса в стандартных условиях).
В биологических системах процессы обычно сопровождаются еще изменением количества вещества и в таком случае:
dU = TdS — pdV + μdN , где
dN – изменение числа частиц,
μ – химический потенциал (градиент).
dG = -SdT + Vdp + μdN
Химический потенциал равен изменению термодинамического потенциала, приходящегося на одну частицу вещества в соответствующем процессе. Он не является термодинамическим потенциалом и служит параметром системы.
Все вышеизложенное разработано для закрытых и изолированных систем, находящихся в состоянии термодинамического равновесия. При этомсостоянии, когда S = max., F = 0, G = 0, ΔS = 0, ΔF = 0, ΔG = 0 , процессы не протекают, материя мертва, так как система не может самопроизвольно выйти из этого состояния.
Живые системы находятся в стационарном состоянии. При этом скорость протекания процессов остается постоянной, то есть ΔS , ΔF, ΔG ≈ 0, но F и G > 0, а S 0.
В стационарном состоянии, если dS = 0, то deS = -diS .
Если изменение энтропии за счет необратимых процессов всегда больше нуля, то свободная энергия Гиббса связана с выражением:
diS / dt = 1/T = -dG / dt > 0
В результате возможно осуществление нескольких вариантов:
- если deS >0 , то и dS >0 ;
- если deS 0,
- если deS |diS| , то dS 0 ).
Неравновесная линейная термодинамика необратимых процессов
Основы неравновесной линейной термодинамики заложены Онзагером и развиты Пригожиным. Согласно ее положениям, допускается, что, даже если система в целом не равновесна, каждая из подсистем может находиться в состоянии равновесия (принцип локального равновесия).
Таким образом, неравновесная линейная термодинамика рассматривает процессы вблизи термодинамического равновесия, когда между потоками и силами существует линейная зависимость.
Изменение энтропии в открытых системах
Для анализа изменений энтропии в открытых системах вводится понятие локальная скорость энтропии (σ) в элементарном объёме (dV).
На основании этого допущения в неравновесной термодинамике можно использовать основные положения равновесной, и тогда изменение энтропии можно считать равным:
dSi / dt = ∫V σ · dV, а так как dSi / dt ≥, то и σ ≥ 0.
Эта функция универсальна для всех термодинамических процессов. Например, для химической реакции она равна: T · dSi / dt = A · υ , где
A – сродство химической реакции,
а υ – скорость реакции.
Таким образом, эта функция, отражающая в общем случае произведение силы (Х) на поток (J) получила название «диссипативная функция»:
JX = T · dSi / dt = T · σ
Если в открытой системе протекает К — процессов, она равна:
Таким образом, и в открытой системе протекание термодинамических процессов всегда сопровождается диссипацией (рассеянием энергии).
Поток ( J ) всегда зависит от силы ( Х ).
Отражая функциональную зависимость, предположим, что:
Функцию всегда можно разложить в ряд Маклорена вблизи равновесия (когда х=0),
J(x) = J(0) + J'(0)/1! · х + J»(0)/2! · х 2 + . + J N (0)/N! · х N
Ограничиваясь вторым слагаемым ряда (членами высшего порядка можно пренебречь) и считая, что x=0 отражает точку равновесия в ней с учетом того, что вблизи равновесия J(0)=0 и, обозначив J1(0)=L, получим:
Таким образом, вблизи равновесия возможна линейная связь между потоком и силой (поэтому эту термодинамику называют линейной), а коэффициент L – феноменологическим коэффициентом.
В любой биологической системе постоянно протекают множество процессов, каждый под действием своей силы Х. Для простоты рассмотрим два процесса: J1 = L11X1 , и J2 = L22X2 .
Онзагер применил принцип взаимности, который в линейной термодинамике гласит, что L12 = L21 , а так как Jk = ∑ Lkn Xn, тогда и Lkn = Lnk .
Если подставить это уравнение в формулу диссипативной функции, получим основное феноменологическое уравнение линейной неравновесной термодинамики.
Теорема Пригожина
В теореме рассматривается основное свойство стационарного состояния, основной критерий его установления, связанный с состоянием энтропии.
Пусть в системе протекают два необратимых процесса: J1 и J2 .
Локальная скорость продукция энтропии для этих процессов складывается из:
Два сопряженных потока (пусть теплоты и вещества) взаимодействуют через коэффициенты:
Тогда с учетом принципа Онзагера /L12 = L21 /:
Исследуем на экстремум величину σ в стационарном состоянии (поток вещества J2=0). Для этого находим частную производную от σ по Х2 при X1 = const:
Так как в стационарном состоянии все потоки равны нулю, то исследуемая функция имеет экстремум.
Для определения знака экстремума берем вторую производную от σ по Х2, и при X1 = const она равна:
а с учетом того, что все коэффициенты L больше нуля, то это минимум. Таким образом, функция, которая всегда dSi /dt ≥ 0 , имеет минимум.
Теорема Пригожина утверждает, что скорость продукции энтропии внутри открытой системы в стационарном состоянии положительна и минимальна.
Она характеризует эволюцию открытой системы вблизи равновесия.
Следствие теоремы Пригожина
Принцип Ле-Шателье. Если термодинамическую систему вывести из состояния равновесия, в ней возникнут силы и потоки, стремящиеся вернуть систему в исходное состояние равновесия.
Нелинейная термодинамика необратимых процессов
Многие процессы протекают вдали от состояния равновесия, когда отсутствуют линейные связи между скоростями и силами.
Пригожин и Виам создали общую термодинамическую теорию роста и развития организмов. Основное её положение заключается в следующем.
Развитие и рост организмов всегда происходят в направлении достижения стационарного состояния, что сопровождаются уменьшением скорости продукции энтропии. То есть в линейной термодинамике основным всё же является утверждение: σ —> min, что определяет состояние системы.
В нелинейной термодинамике продукция энтропии состоит из двух составляющих:
при постоянстве потоков dJk / dt = 0 и dσ / dt = dxσ / dt.
Таким образом, основное неравенство нелинейной термодинамики: dxσ / dt ≤ 0 отражает универсальный эволюционный критерий открытой системы вдали от равновесия. Условие устойчивости отражает флуктуации системы.
Флуктуации ∂xσ могут быть как положительными, так и отрицательными ∂xσ > 0
В стационарном состоянии положительные флуктуации быстро исчезают за счет стремления скорости продукции энтропии к минимуму.
Отрицательные флуктуации являются следствием неустойчивости стационарного состояния системы и приводят к стационарному состоянию с уменьшенной энтропией (это эволюция).
В индивидуальном развитии организма есть три такие стадии:
- оогенез;
- регенерация;
- злокачественный рост.
Видео:«Пригожина убьют»: что ждет главу ЧВК «Вагнер» #пригожин #война #путин #shortsСкачать

Неравновесная термодинамика
Выше изложенные положения классической (равновесной) ТД верны для изолированных и закрытых систем и описывают системы, находящиеся в состоянии термодинамического равновесия.
Неравновесная термодинамика подразделяется на линейную и нелинейную.
Линейная рассматривает процессы, протекающие вблизи равновесия.
Нелинейная – вдали от него.
Уравнение Пригожина и его анализ:
Уравнение Пригожина позволяет решить вопрос применимости второго закона термодинамики к открытым системам.
Согласно II-му закону ТД:
Пригожин предложил разбить общее изменение энтропии на два слагаемых:
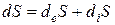
где 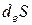
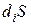
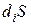
В стационарном состоянии, если 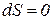
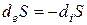
Если изменение энтропии за счет необратимых процессов всегда больше нуля, то свободная энергия Гиббса связана с выражением:
В результате возможно осуществление нескольких вариантов:
1) Если 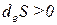
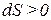
2) Если 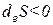
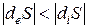
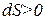
3) Если 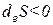
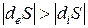
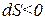
Последний вариант является лишь кажущимся отклонением от II-го закона термодинамики, так как процесс обмена: 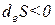
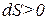
Неравновесная линейная термодинамика необратимых процессов
Основы неравновесной линейной термодинамики заложены Онзагером и развиты Пригожиным. Согласно ее положениям допускается, что, даже если система в целом не равновесна, каждая из подсистем может находиться в состоянии равновесия (принцип локального равновесия).
Таким образом, неравновесная линейная термодинамика рассматривает процессы вблизи термодинамического равновесия, когда между потоками и силами существует линейная зависимость.
Изменение энтропии в открытых системах
Для анализа изменений энтропии в открытых системах вводится понятие локальная скорость энтропии s в элементарном объёме 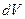
На основании этого допущения, в неравновесной термодинамике можно использовать основные положения равновесной и тогда изменение энтропии можно считать равным:
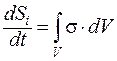
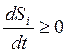

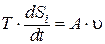
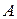
а u – скорость реакции.
Таким образом, эта функция, отражающая в общем случае произведение силы – 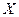
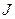
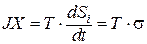
Если в открытой системе протекает 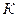
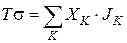
Таким образом, и в открытой системе протекание термодинамических процессов всегда сопровождаются диссипацией (рассеянием энергии).
Поток 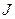
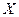
Отражая функциональную зависимость, предположим, что:
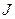
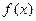
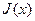
Функцию всегда можно разложить в ряд Маклорена вблизи равновесия (когда 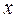
Ограничиваясь вторым слагаемым ряда (членами высшего порядка можно пренебречь) и считая, что x= 0 – отражает точку равновесия в ней, с учетом того, что вблизи равновесия J(0)=0 и, обозначив J 1 (0)=L, получим:
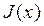
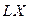
Таким образом вблизи равновесия, возможна линейная связь между потоком и силой (поэтому эту термодинамику называют линейной), а коэффициент L – феноменологическим коэффициентом.
В любой биологической системе постоянно протекают множество процессов, каждый под действием своей силы Х.
Для простоты рассмотрим два процесса:
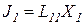
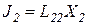
Естественно, что они влияют друг на друга:
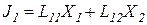
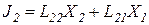
Онзагер применил принцип взаимности, который в линейной термодинамике гласит, что 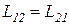
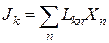
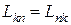
Если подставить это уравнение в формулу диссипативной функции, получим основное феноменологическое уравнение линейной неравновесной термодинамики.
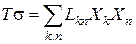
В теореме рассматривается основное свойство стационарного состояния, основной критерий его установления, связанный с состоянием энтропии.
Пусть в системе протекают два необратимых процесса:
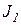
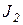
Локальная скорость продукция энтропии для этих процессов складывается из них:
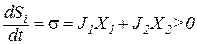
Два сопряженных потока (пусть теплоты и вещества) взаимодействуют через коэффициенты:
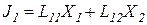
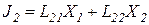
Тогда с учетом принципа Онзагера / 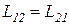
Теперь исследуем на экстремум величину s в стационарном состоянии (поток вещества 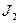
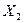
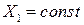
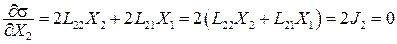
Так как в стационарном состоянии все потоки равны нулю, исследуемая функция имеет экстремум.
Для проверки ее на знак берем вторую производную от s по 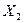
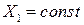
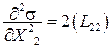
а с учетом того, что все коэффициенты L больше нуля, то это минимум.
Таким образом, функция, которая всегда 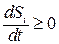
Теорема Пригожина утверждает, что скорость продукции энтропии внутри открытой системы в стационарном состоянии положительна и минимальна.
Она характеризует эволюцию открытой системы вблизи равновесия.
Следствие теоремы Пригожина.
Принцип Ле-Шателье.Если термодинамическую систему вывести из состояния равновесия, в ней возникнут силы и потоки, стремящиеся вернуть систему в исходное состояние равновесия.
Нелинейная термодинамика необратимых процессов.
Многие процессы протекают вдали от состояния равновесия, когда отсутствуют линейные связи между скоростями и силами.
Пригожин и Виам создали общую термодинамическую теорию роста и развития организмов.
Основное её положение заключается в следующем:
Развитие и рост организмов всегда происходит в направлении достижения стационарного состояния, что сопровождается уменьшением скорости продукции энтропии. То есть в линейной термодинамике основным всё же является утверждение: 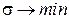
В нелинейной термодинамике продукция энтропии состоит из двух составляющих:
при постоянстве потоков 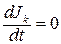
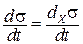
Таким образом, основное неравенство нелинейной термодинамики: 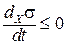
Флуктуации 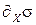
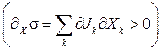
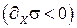
В стационарном состоянии положительные флуктуации быстро исчезают за счет стремления скорости продукции энтропии к минимуму.
Отрицательные флуктуации являются следствием неустойчивости стационарного состояния системы и приведут к стационарному состоянию с уменьшенной энтропией (это эволюция).
В индивидуальном развитии организма есть три такие стадии:
Видео:Пригожин жив? Где было снято последнее видео с основателем ЧВК Вагнер, которое наделало столько шумаСкачать

Стационарное состояние живого организма
Видео:Первое заявление Пригожина после мятежаСкачать

Стационарное состояние живого организма
Состояние системы, при котором ее параметры не изменяются в течение длительного времени, но происходит обмен веществом и энергией с окружающей средой.
Стационарное состояние в живых организмах достигается путем взаимной компенсации всех процессов, связанных с поступлением, удалением и превращением веществ и энергии.
Св-ва стац. состояния системы: стремление системы к мин. ежесекундному приросту энтропии; определеннная внутр. стабильность и упорядоченность.
Принцип Ле-Шателье: если система устойчива, то при отклонении в системе возникают силы, стремящиеся вернуть ее в исходное положение.
Стационарное состояние и термодинамическое равновесие
Стац. сосст — сост. системы при кот. ее параметры не изм. в течении длит. времени но происходит обмен веществом и энергией со средой.
ТД равновесие — сост. системы при кот. ее параметры не изм. и она не обменивается с окр. средой ни веществом ни энергией.
Различие между системами:
| Термодинамическое равновесие | Стационарное состояние |
| Отсутствие обмена с окр. средой веществом и энергией | Непрерывный обмен с окр. средой веществом и энергией |
| Энтропия постоянна и соотв. max возможному в данных условиях значению | Энтропия постоянна, но не равна max возможному в данных условиях значению |
| Полное отсутствие в системе каких-либо градиентов | Наличие постоянных по величине градиентов |
| Не требуется затраты свободной энергии | Необходимы постоянные затраты энергии |
| Система нереакционноспособна и не совершает работу против внешних сил | В системе совершаются необратимые реакции, ее работоспособность постоянна и не равна нулю |
Живой организм может изменить уровень стационарного состояния в результате воздействия окр. среды и при патологических процессах.
Одной из важнейших характеристик био. систем является устойчивость стационарных состояний, при отклонении системы от стационарного уровня в ней возникают силы, стремящиеся вернуть ее в первоначальное положение.
В момент смерти организм находится в сост. ТД равновесия
Уравнение Пригожина
в стац. состоянии при фиксированных внеш. параметрах скорость продукции энтропии в открытой системе, обусловленная протеканием необратимых процессов, постоянна во времени и минимальна по величине:
Т.о. стац. состояние характеризуется мин. рассеянием энергии. В соответствии с теоремой Пригожина для поддержания стац. состояния тратится некоторое кол-во энергии, причем самое минимальное. Организм стремится работать на самом выгодном энергетическом режиме. При этом энтропия возрастает с минимальной скоростью.
Основные понятия и особенности кинетики биологических процессов
базируются на общих теоретических положениях хим. кинетики, изучающей скорости хим. реакций. Фундаментальное понятие хим. кинетики — хим. реакция, представляющая собой совокупность актов перегруппировки межатомных связей.
Хим. реакции можно разделить на:
1) Гомогенныепротекают с одинаковой скоростью в любом элементарном объеме данной фазы;
2) гетерогенные— на границе раздела фаз, и скорость их определяется скоростью подачи реагирующих веществ на поверхности раздела фаз.
Катализаторыповышают скорость спонтанно протекающих реакций. Если вещество инициирует реакцию, оно называется инициатором, если ускоряет каталитическую реакцию, то его относят к активаторам. Соединения, понижающие скорость каталитической реакции или полностью подавляющие — ингибиторами.
Под кинетикой реакции понимают зависимость скорости реакции от концентрации реагирующих веществ, температуры и других параметров.
Реакции называются последовательными, если продукт одной из реакций является исходным веществом для другой. A 

Сопряженной называют реакцию, которая происходит при одновременном протекании другой реакции.
Цепная реакция — это самоподдерживающаяся химическая реакция, при которой первоначально появляющиеся продукты принимают участие в образовании новых промежуточных и конечных продуктов.
Параллельными называют совместно протекающие реакции, если, по крайней мере, одно исходное вещество этих реакций является общим.
Видео:Последнее послание Пригожина. Смерть вагнеровца официально подтвердили: деталиСкачать

Стационарные неравновесные состояния. Термодинамика биологических процессов
Принцип Ле Шателье
Напомним, что состояние системы называется равновесным, если в этом состоянии все параметры системы имеют определенные значения и остаются при неизменных внешних условиях постоянными сколь угодно долго. Система может быть выведена из равновесия воздействием извне.
Процессам, нарушающим равновесие системы, противостоит внутренняя релаксация. Например, в случае разреженных газов внутренняя релаксация обусловлена столкновением между молекулами. Поэтому после прекращения внешнего воздействия система возвращается в равновесное состояние. Время, необходимое для такого возвращения, называется временем релаксации.
Если возмущающие процессы менее интенсивны, чем релаксационные, то в малых объемах системы наблюдается локальное равновесие.
Например, если газ поместить между плоскостями, нагретыми до разных температур, то система в целом не будет равновесной, температура системы в разных точках будет различной. Однако процесс теплопроводности достаточно медленный и в системе будут области с локальным равновесием. Локальное равновесие может наблюдаться и в случае медленного изменения внешнего воздействия для времен, бóльших времени элементарного релаксационного процесса, формирующего равновесие.
В сложной системе, состоящей из большого числа подсистем, возникает большое число связей между ними.
В такой системе из-за внутренних взаимодействий возникает эффект системности: появление большого количества новых свойств, которых нет у ее частей. На пути любой достаточно сложной системы к равновесию, которое характеризуется максимумом энтропии, встречаются обстоятельства, не позволяющие это сделать.
Такими обстоятельствами могут выступать граничные условия (например, постоянная разность температур на границах). В этом случае система с течением времени переходит в квазистационарное состояние. Таким образом, в неравновесной термодинамике появилось новое понятие стационарное (т.е. не зависящее от времени) неравновесное состояние.
В стационарных неравновесных состояниях характеристики системы не зависят от времени, поэтому и энтропия от времени не зависит. Но энтропия все время возникает, поскольку потоки и силы в системе отличны от нуля.
Полная энтропия будет постоянной только при поступлении в систему извне отрицательной энтропии или негэнтропии, которая компенсирует производство энтропии внутри системы.
В стационарном неравновесном состоянии уменьшается производство энтропии. Теорема о минимуме производства энтропии в стационарном неравновесном состоянии, сформулированная Пригожиным, отражает внутреннюю устойчивость неравновесных систем, их своеобразную инерционность.
Устойчивость стационарных состояний с минимальным производством энтропии связана с принципом, сформулированным в 1884 г.
Ле Шателье и обобщенным в 1887 г. немецким физиком К. Брауном. Принцип Ле Шателье–Брауна в современной интерпретации означает, что система, выведенная внешним воздействием из состояния с минимальным производством энтропии, стимулирует развитие процессов, направленных на ослабление внешнего воздействия.
Принцип локального равновесия и теорема о минимуме производства энтропии в равновесных системах были положены в основу современной термодинамики необратимых процессов.
Видео:Пригожин ГРУЗ 200... Россиянам "ГРУСТНО"Скачать

Стационарное состояние. Теорема Пригожина
Стационарным называют такое состояние открытой системы, при котором основные макроскопические параметры системы остаются постоянными. Необходимы различные стационарные состояния от равновесного состояния.
Отличительные признаки стационарного и равновесного состояния
| Равновесное | Стационарное |
| G и работоспособность системы минимальные. | 1. G и работоспособность системы постоянны, но не минимальны. |
| 2.Энтропия в системе максимальна. | 1. Энтропия в системе постоянна, за счет равенства продукции и потока энтропии. |
В состоянии равновесия в системе прекращаются все процессы, кроме теплового движения молекул, при этом выравниваются все градиенты.
В стационарном состоянии идут химические реакции, диффузия, перенос ионов и другие процессы, но они так стабилизированы, что состояние системы в целом не изменяется.
В стационарном состоянии существуют градиенты между отдельными частями системы, но они сохраняют постоянные значения. Это возможно только при условии, что система из окружающей среды получает вещество и G , а отдает продукты реакции и выделяющееся тепло.
Термодинамическим условием стационарного состояния является равенство между продукцией энтропии, произведенной организмом, и потоком энтропии, то есть:

Термодинамика открытых систем позволяет вскрыть еще одну причину целесообразности стационарного состояния для биологической системы, которая сформулирована в теореме Пригожина:
«В стационарном состоянии продукция энтропии имеет постоянное и минимальное из всех возможных значений, то есть»:
Теорема Пригожина показывает, что в стационарном состоянии диссипация Gпроисходит с меньшей скоростью, чем в любых других состояниях, стало быть, в стационарном состоянии G системы расходуется наиболее экономно и поэтому требуется минимальная компенсация ее затрат, то есть, КПД системы в стационарном состоянии максимален.
Необходимо отметить, что теорема Пригожина справедлива только для таких состояний, которые мало отличаются от стационарных.
В этом случае, скорости всех процессов выражаются линейными уравнениями (уравнения 1 порядка).
Теорема Пригожина дает термодинамические критерии эволюции линейным системам, которые формулируются следующим образом:
«Открытая линейная система, если она не находится в стационарном состоянии, будет изменяться до тех пор, пока скорость продукции энтропии в ней не приобретет минимальное значение из всех возможных, то есть, пока величина диссипативная функции не примет минимальное значение».
Таким образом, второе начало термодинамики для живых организмов можно представить в следующем виде:
I, II, III — второе начало термодинамики для живых организмов.
Видео:Пригожин и его враги: кто мог ликвидировать главу «Вагнера» | Путин, Шойгу, УкраинаСкачать

Термодинамика биологических процессов
Стационарное состояние живых ТД систем, его отличие от ТД равновесия; баланс энтропии и свободной энергии. Условия перехода живых систем на новый стационарный уровень.
Зависит от 3-х параметров: -S (энтропия), -U (своб.
Стац. сост. – сост., когда параметры системы (U, S) с теч. времени остаются неизменными, но происходит обмен в-вом и Е, т.е. сост. сист. при кот. не происх. изм. ТД параметров.
Изолированные сист.: ∆S=0 или >0.
Для равновесного сост.
S стремится к мах, U=0. Стац. сост. отличается тем, что S ≠ мах, а является постоянной величиной, S=const, U не равняется 0, U=const. Ежесекундный прирост энтропии стремится к min. Любая живая система может находиться только в стац.
сост. Если достигнуто состояние ТД равновесия — это уже не живая система. Качество стационарного состояния может быть различным.
В открытых системах:
S состоит из двух показателей.
Si – внутри самой сист., S — самой системы, Se – внешняя среда.
dS=dSi+dSe (d – это ∆ — это изменение)
Когда dSe > dSi и dSe 0.
Состоянию ТД равновесия — характерно мах значение S (S=max), U=0, т.е. Е, которая расходуется на совершение А.
Сходство: стац. и равновесное состояния не зависят от времени.
Отличия стац. сост. от равновесия (из конспекта):
1) своб. Е (∆G) в стац. сост. есть величина постоянная во времени и не равна 0.
В ТД равн. ∆G=const, но ∆G =0 => открытые сист., если вывести из стац. сост. могут совершать работу; при ТД равновесии не способны совершать работу.
В стац. сост. =const, но она не max. (∆G) ∆S ≠ max = const.
3) . в стац. сост. проявляется кинетический параметр (фактор) (изменение энтропии во времени) dS/dt = dSi/dt + dSe/dt.
* постоянный обмен энергией с окружающей средой
* постоянно тратится свободная энергия на поддержание состояния
* т/д потенциалы постоянны, G и F не равны 0
* энтропия постоянна, но не максимальна
* отсутствует поток вещества и энергии в окружающую среду и обратно
* на поддержание этого состояния не затрачивается свободная энергия
* работа способности системы равна 0, т/д потенциалы равны 0
* в системе отсутствуют градиенты
Переход на новый стац.

Нижняя стрелочка – это старый стац. уровень.
Верхняя стрелочка – это новый стац. уровень.
2) «ложный старт» — усиление или уменьшение О2, выращивание лука с О2 и без. График. С О2 – аэробный распад углеродов. Без О2 – обмен в-в переходит на анаэробный путь.
А если потом снова дать О2 – то получится график 2 (то что обведено кружочком – там осущ-ся уничтожение продуктов анаэробного пути). Пример для чела: пока не расщепится молочная к-та осуществлять работу дальше нельзя.
17. Теорема Пригожина и направленность эволюции биосистем.
Энтропия и биологический прогресс.
Стац. сост. хар-ся min ежесекундным приростом энтропии (благодаря этому происходит эволюция).
Теорема: при постоянных внеш. усл. в системе, находящейся вблизи положения ТД равновесия в стац. сост., скорость возрастания энтропии, за счёт необходимости внутр. процессов, принимает постоянное минимальное значение отличное от нуля.
Или: В стационарных состояниях при фиксированных внешних параметрах локальная продукция энтропии в открытой т/д системе стремится к минимальному значению.
Энтропия – мера рассеивания свободной энергии, следовательно любая открытая т/д система в стационарном состоянии стремится к минимальному рассеиванию свободной энергии.
Если в силу причин система отклонилась от стационарного состояния, то вследствие стремления системы к минимальной энтропии, в ней возникают внутренние изменения, возвращающие ее в стационарное состояние.
🎬 Видео
Версии крушения самолёта Пригожина: как расследуют дело и погиб ли основатель ЧВКСкачать

Пригожина убили? #zapovednikshow #shorts #пригожинСкачать

Пригожин РАСКРЫЛ настоящие ЦЕЛИ "СВО"Скачать

Пригожин жив благодаря Путину. Геннадий ГудковСкачать

После этой задачи Пригожин начал ...Скачать

Окончательный приговор! Пригожина списали за ненадобностью. Владимир ОсечкинСкачать

Пригожин думал, что Путин его поддержит. Аббас ГаллямовСкачать

В России вспоминали Евгения Пригожина на 40-й день после его гибелиСкачать

Ну вот и все! Пригожин допрыгался! Владимир ОсечкинСкачать
«Блокируем Ростов и идем в Москву»: переговоры Пригожина и замминистра обороны Евкурова #пригожинСкачать

Последний разговор с Пригожиным и как была устроена его империя. Специальный выпускСкачать

Пригожин нанёс Путину нокаутирующий удар. Ходорковский о трусливом ПригожинеСкачать

Анализ 6 ПИАРНЫХ ТРЮКОВ Евгения ПригожинаСкачать

"Вагнер" списали: замена ЧВК найдена. Раскрыта главная причина ликвидации ПригожинаСкачать