Уравнение поверхности равного давления вращающийся сосуд с жидкостью (3 видео)

Поверхность равного давления

Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.

Рассмотрим два примера такого относительного покоя.

Жидкость в неинерциальных системах отсчета

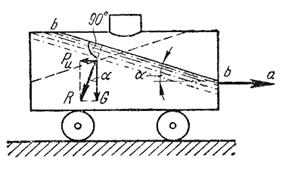
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.15).

Рис. 2.15. Движение цистерны с ускорением

К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G=mg и сила инерции P_u = ma.

Равнодействующая этих сил R = ((mg) 2 +(ma) 2 ) 1/2 направлена к вертикали под углом α, тангенс которого равен tga = a/g.

Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости.

Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рис.2.6, пунктир).

Относительный покой жидкости во вращающемся сосуде

В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (рис.2.16), например, в сепараторах и центрифугах, применяемых для разделения жидкостей.

В этом случае на любую частицу жидкости при ее относительном равновесии действуют массовые силы:

где r — расстояние частицы от оси вращения, а ω — угловая скорость вращения сосуда.

Рис. 2.16. Вращение сосуда с жидкостью

Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом, который описывается уравнением

Закон изменения давления во вращающейся жидкости в функции радиуса и высоты записывается в виде

Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально высоте z.

Равновесие газа

Уравнения равновесия, выведенные для жидкости, имеют общий характер и могут быть использованы при расчете сжимаемой жидкости или газа.

Для газа, находящегося в равновесии, любая горизонтальная плоскость, проведенная внутри занимаемого газом объема, будет поверхностью равного давления (рис. 2.11).

В однородной газовой среде (ρ = const), распределение давления не отличается от распределения давления в покоящейся капельной жидкости.

Определив постоянную интегрирования из граничных условий, например (см. рис. 2.11) на поверхности земли z=z₀ и р=р₀,получим уравнение

где z — расстояние от плоскости сравнения 0′-0′ до рассматриваемой точки (высота точки М); z₀ — расстояние от плоскости сравнения 0′-0′ до поверхности с заданным давлением р=р_0.

Рис. 2.11. Равновесие газа в поле силы тяжести

Уравнения (2.17) и (2.18) показывают, что в поле силы тяжести изменение давления газа будет, так же как и в капельной жидкости, определяться только изменением расстояния от плоскости сравнения до рассматриваемой точки. Полученное уравнение показывает, что с увеличением высоты до рассматриваемой точки давление уменьшается, так как в выбранной системе координат z>z₀.

Характер же этого изменения будет корректироваться в зависимости от закона изменения внутреннего состояния газа.

Видео:Урок 47 (осн). Расчет давления жидкости на дно и стенки сосудаСкачать

Равномерное вращение сосуда с жидкостью

Сила давления жидкости на плоскую стенку

Используем основное уравнение гидростатики (2.1) для нахождения полной силы давления жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом a (рис. 2.8).

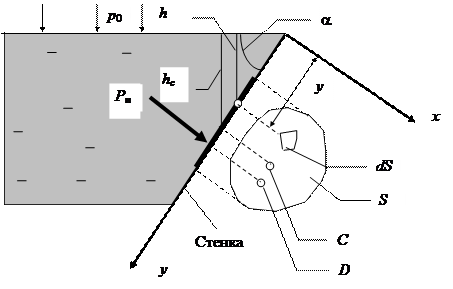Уравнение поверхности равного давления вращающийся сосуд с жидкостью

Вычислим полную силу P давления, действующую со стороны жидкости на некоторый участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S.

Ось 0x направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось 0y – перпендикулярно этой линии в плоскости стенки.

Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке dS:

где p₀ – давление на свободной поверхности; h – глубина расположения площадки dS.

Для определения полной силы P выполним интегрирование по всей площади S:

где y – координата центра площадки dS.

Последний интеграл, как известно из механики, представляет собой статический момент площади S относительно оси Ox и равен произведению этой площади на координату ее центра тяжести (точка С), т. е.

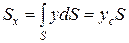
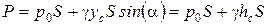
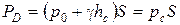
Следовательно, , где h_c – глубина погружения центра тяжести площади S. В результате имеем:

, (2.6)

т. е. полнаясила давления жидкости на плоскую стенку равна произведению гидростатического давления (определяемого давлением на свободной поверхности жидкости и глубиной погружения центра тяжести площади S) в центре тяжести площади этой стенки на ее площадь.

Найдем положение точки приложения силы избыточного давления.

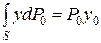
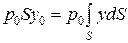
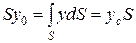
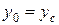
Так как внешнее давление p₀ передается всем точкам площади S одинаково, то равнодействующая этого давления будет приложена в центре тяжести площади S: ; ; , т.е. .

Для нахождения точки приложения силы избыточного давления жидкости (точка D) применим уравнение механики, согласно которому момент равнодействующей силы давления относительно оси 0x равен сумме моментов составляющих сил:

; ; ,

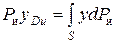
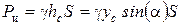
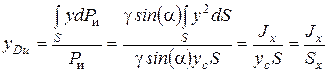
где 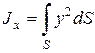– момент инерции площади S относительно оси 0x.

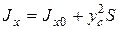
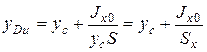
Учитывая, что (J_x₀ – момент инерции площади S относительно оси, проходящей через центр тяжести площади S и параллельной 0x), получим

. (2.7)

Таким образом, точка приложения силы P_и расположена ниже центра тяжести площади стенки на расстояние .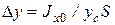

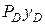
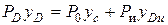
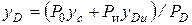
Определим центр давления y_D от действия сил давления на свободной поверхности и избыточного давления. Запишем уравнение моментов относительно верхней точки пластины и определим как результирующий момент от действия моментов перечисленных выше сил давления.

; .

В частном случае, когда стенка имеет прямоугольную форму, причем одна из сторон прямоугольника совпадает со свободной поверхностью жидкости, положение центра давления находится из геометрических соображений. Так как эпюра давления жидкости на стенку изображается прямоугольным треугольником (рис. 2.10), центр тяжести которого отстоит от основания на 1/3 высоты b треугольника, то и центр давления жидкости будет расположен на том же расстоянии от основания: , . Если стенка вертикальная, то .

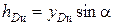
Рис. 2.10

В машиностроении часто приходится сталкиваться с действием силы давления на плоские стенки, например на стенки поршней или цилиндров гидравлических машин. Обычно p₀ при этом бывает настолько высоким, что центр давления можно считать совпадающим с центром тяжести площади стенки. Найдем статические моменты, моменты инерции и положения центров тяжести для прямоугольной и треугольной пластин.

Закон Архимеда

Пусть в жидкость погружен параллелепипед объемом W (рис. 2.13).

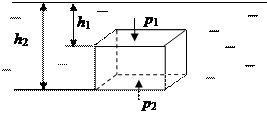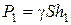
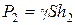
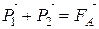
На него действуют следующие силы: сверху сила давления от столба жидкости , снизу – , где S – площади нижней и верхней граней параллелепипеда; равнодействующая сил давлений, действующих на боковые грани, равна нулю, так как они равны и противоположно направлены. Спроектируем силы на вертикальную ось, вес тела учитывать не будем. Отметим, что согласно закону Паскаля давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково, поэтому давление на внешней поверхности действует по всем граням одинаково и во взаимно противоположных направлениях, поэтому результирующая сила равна нулю.

, откуда

; .

Закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной этим телом.

В случае тела произвольной формы, погруженного в жидкость, закон Архимеда выводится, привлекая дополнительные рассуждения.

Равномерное вращение сосуда с жидкостью

Вращение сосуда с жидкостью вокруг вертикальной оси

Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему постоянную угловую скорость w вращения вокруг вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее видоизменится: в центральной части уровень жидкости понизится, у стенок – повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения (рис. 2.15).

На жидкость в этом случае будут действовать две массовые силы, сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны g и . Равнодействующая массовая сила j увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, поэтому угол наклона поверхности к горизонту возрастает с увеличением радиуса. Найдем уравнение положения свободной поверхности.

Учитывая, что сила нормальна к свободной поверхности, получим , отсюда или после интегрирования .

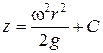
В точке пересечения свободной поверхности с осью вращения C=h и r=0, поэтому окончательно будем иметь

, (2.10)

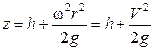
где .

Таким образом, свободная поверхность жидкости является параболоидом вращения. Максимальную высоту подъема жидкости можно определить, используя выражение (2.10) и исходя из равенства объемов неподвижной жидкости и жидкости во время вращения.

Запишем закон изменения давления во вращающейся жидкости в функции радиуса и глубины относительно верхней точки жидкости (без вывода):

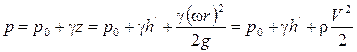
Вращение сосуда с жидкостью вокруг горизонтальной оси

При таком вращении угловая скорость w столь велика, что 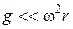(действие силы тяжести можно не учитывать). Закон изменения давления в жидкости для этого случая получим из рассмотрения уравнения равновесия элементарного объема с площадью основания dS и высотой dr, взятой вдоль радиуса (рис. 2.16). На выделенный элемент жидкости действуют силы давления и центробежная сила.

Рис. 2.16

Обозначив давление в центре площадки dS, расположенной на радиусе r, через p, а в центре другого основания объема (на радиусе r + dr) через p + dp (разложили p в ряд Тейлора, но так как в данном случае p зависит только от r, то dr/dr сократился), получим следующее уравнение равновесия выделенного объема в направлении радиуса

или .

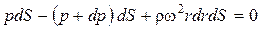
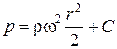
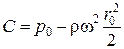
После интегрирования получим . Постоянную C найдем из условия, что при r = r₀ p = p₀, следовательно, .

Подставив ее значение в предыдущее уравнение, получим связь между p и r в следующем виде:

. (2.11)

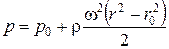
Очевидно, что поверхностями уровня в данном случае будут цилиндрические поверхности с общей осью – осью вращения жидкости.

Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к его оси вращения. Для этого определим силу давления, приходящуюся на элементарную кольцевую площадку радиусом r и шириной dr. Используя формулу (2.11), получим

а затем следует выполнить интегрирование в требуемых пределах:

Если 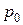равно внешнему давлению, то .

При большой скорости вращения жидкости получается значительная суммарная сила давления F_б на боковую стенку. Это используется в некоторых фрикционных муфтах, где для сцепления двух валов требуется создание больших сил давления.

Приведем выражение для определения силы F_б без вывода:

, где – длина цилиндра.

Видео:Физика 7 класс (Урок№20 - Расчёт давления жидкости на дно и стенки сосуда.)Скачать

Поверхность жидкости во вращающемся сосуде

Определим, какую форму принимает поверхность жидкости в равномерно вращающемся сосуде. Свободная поверхность и в здесь будет поверхностью уровня, только на этот раз это будет уже не горизонтальная плоскость, поскольку на жидкость из объемных сил действует не только сила тяжести.

При равномерном вращении сосуда с жидкостью поставленную задачу можно рассматривать как гидростатическую, жидкость будет находиться в покое относительно стенок сосуда, т. е. здесь будет наблюдаться случай «относительного покоя». При этом жидкость будет находиться в равновесии под действием двух объемных сил: силы тяжести и силы инерции – центробежной силы.

На каждую частицу жидкости во вращающемся сосуде действуют обе эти силы.

Центробежная сила, действующая на частицу жидкости, находящуюся в некоторой произвольной точке М (рис. 2.7), для кругового движения определится по формуле

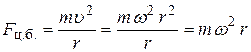
Здесь r – радиус окружности (расстояние от точки до оси вращения), по которой вращается частица жидкости, находящаяся в точке М,

ω – угловая скорость вращения,

m – масса частицы жидкости.

Удельная центробежная сила, т. е. сила, отнесенная к единице массы, будет равна

Проекции удельной центробежной силы на оси координат определятся как (рис. 2.7)

Проекции удельной силы тяжести на оси

Суммарно для проекций удельных объемных сил, действующих на частицу жидкости, получаем

Вспомним дифференциальное уравнение равновесия жидкости:

Подставим в него значения проекций объемных сил:

Проинтегрируем уравнение, считая ρ величиной постоянной. Имеем

Заметим, что при вращении жидких частиц по круговым траекториям

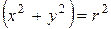
Для определения константы интегрирования сформулируем граничные условия. Обратим внимание на то, что при вращении свободная поверхность жидкости примет симметричную вогнутую форму. Расположим начало координат в низшей точке свободной поверхности. На свободной поверхности жидкости давление равно атмосферному.

Тогда граничное условие формулируется так:

при x = y = z = 0 давление p = p_атм.

Определяя из этого условия константу интегрирования, получим:

Уравнение для определения давления примет вид:

(2.10)

По этой формуле можно вычислить давление в любой точке внутри объема жидкости, находящейся в сосуде, вращающемся с постоянной угловой скоростью.

Как определить форму свободной поверхности жидкости? Свободная поверхность является поверхностью уровня, т. е. поверхностью равного давления. Давление во всех ее точках равно атмосферному p = p_атм. Используя это условие, из уравнения (2.10) получаем

где индекс «п» относится к координатам точек, находящихся на поверхности жидкости. Окончательно имеем

(2.11)

Уравнение (2.11) дает зависимость вертикальной координаты точек, расположенных на свободной поверхности жидкости, от расстояния до оси вращения: . Это и есть уравнение свободной поверхности жидкости, находящейся в равномерно вращающемся сосуде. Видно, что форма свободной поверхности – параболоид вращения с вертикальной осью симметрии.