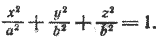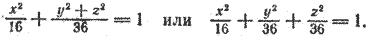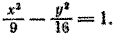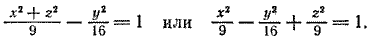Уравнение поверхности образованной вращением линии вокруг оси ох (5 видео)

Уравнение поверхности образованной вращением линии вокруг оси ох

Глава VI. Простейшие криволинейные поверхности и тела вращения.

§ 75*. Поверхности вращения

1. Пусть в плоскости р задана кривая L и некоторая прямая l. Поверхность, которая получается вращением кривой L вокруг прямой l, называется поверхностью вращения.

Пусть кривая L лежит в плоскости хОу (рис. 216) и имеет уравнение

y = f(x), х [а; b]. (1)

Найдем уравнение поверхности, которая получится вращением кривой L вокруг оси Ох (рис. 217).

Очевидно, точка M с координатами (х; у; z), где х [а; b], принадлежит искомой поверхности вращения тогда и только тогда, когда

Действительно, точки (х; у; z) и (х; f(x); 0) лежат на одной окружности с центром в точке (х; 0; 0).

Таким образом, уравнение поверхности, полученной вращением кривой (1) вокруг оси Ох, имеет вид

y 2 + z 2 = (f(x)) 2 , х [а; b]. (2)

Заметим, что уравнение (2) получается из уравнения (1) следующим образом:
обе части уравнения (1) возводятся в квадрат и y 2 заменяется на y 2 + z 2 ,

В частности, если кривая L задана уравнением

то уравнение поверхности, полученной вращением этой кривой вокруг оси Ох, имеет вид

т. е. просто y 2 заменяем на y 2 + z 2 .

2. Поверхность, которая получается вращением эллипса вокруг одной из его осей, называется эллипсоидом вращения.

Пусть в плоскости хОу эллипс задан уравнением

(5)

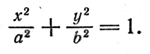
Составим уравнение поверхности, полученной вращением его вокруг оси Ох. Уравнение эллипса (5) приводится к виду (3), следовательно, для получения уравнения эллипсоида вращения достаточно в уравнении (5) y 2 заменить на y 2 + z 2 . После замены получим

(6)

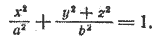
Это уравнение обычно записывают так:

При а > b уравнение (6) определяет эллипсоид вращения, вытянутый вдоль оси Ох (рис. 218), при а 2 на y 2 + z 2 , получим искомое уравнение эллипсоида вращения:

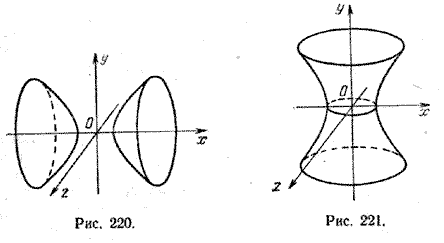
3. Поверхность, которая получается вращением гиперболы вокруг одной из ее осей, называется гиперболоидом вращения. При вращении гиперболы вокруг ее действительной оси получается двуполостный гиперболоид вращения (рис. 220), а при вращении гиперболы вокруг ее мнимой оси получается однополостный гиперболоид вращения (рис. 221).

Пусть в плоскости хОу гипербола задана уравнением

(7)

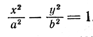
Составим уравнение поверхности, полученной вращением гиперболы вокруг ее действительной оси Ох. Уравнение гиперболы (7) приводится к виду (3); следовательно, для получения уравнения поверхности двуполостного гиперболоида вращения достаточно в уравнении гиперболы (7) y 2 заменить на y 2 + z 2 . После замены получим

(8)

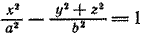
При вращении гиперболы (7) вокруг ее мнимой оси нужно в уравнении (7) x 2 заменить на x 2 + z 2 ; после замены получим

(9)

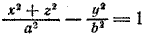
Задача 2. Гипербола с полуосями а = 3 и b = 4 вращается вокруг своей мнимой оси, совпадающей с осью Оу. Центр гиперболы совпадает с началом координат. Составить уравнение поверхности, полученной при вращении этой гиперболы.

Составим уравнение гиперболы:

Чтобы получить уравнение гиперболоида вращения, в уравнении гиперболы x 2 заменим на x 2 + z 2 . После замены получим

4. Поверхность, которая получается вращением параболы вокруг ее оси симметрии, называется параболоидом вращения (рис. 222).

Пусть на плоскости хОу парабола задана уравнением

Для получения уравнения поверхности вращения нужно в уравнении (10) x 2 заменим на x 2 + z 2 ; после замены получим

Отметим одно замечательное свойство этой поверхности. Если внутреннюю поверхность параболоида вращения сделать зеркальной, а в ее фокусе (фокусом параболоида вращения называется фокус вращаемой параболы) поместить источник света, то все лучи света, отражаясь от поверхности параболоида, пойдут параллельно оси параболоида.

Это свойство широко используется при изготовлении светоотражающих устройств (прожекторов, фар автомобиля, кинопроекторов и других приборов).

Задача 3. Составить уравнение поверхности, полученной вращением параболы y 2 = 2х вокруг оси Ох.

Чтобы составить уравнение параболоида вращения, полученного вращением параболы вокруг оси Ох, нужно в уравнении y 2 = 2х заменить y 2 на y 2 + z 2 , после замены получим

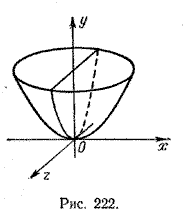
5. Если вращать прямую, параллельную какой-либо оси координат, вокруг этой оси, то получится круговая цилиндрическая поверхность.

Пусть дана прямая, лежащая в плоскости yOz и имеющая уравнение у = а. Легко видеть, что поверхность вращения этой прямой вокруг оси Oz имеет уравнение

Эта цилиндрическая поверхность изображена на рис. 223.

Задача 4. Составить уравнение цилиндрической поверхности, полученной вращением прямой у = 3, лежащей в плоскости хОу вокруг оси Ох.

В уравнении y 2 = 3 2 заменим y 2 на y 2 + z 2 , в результате получим

6. Пусть дана прямая, лежащая в плоскости yOz и проходящая через начало координат:
y = kz, k =/= 0.

Очевидно, уравнение поверхности вращения этой прямой вокруг оси Oz имеет вид

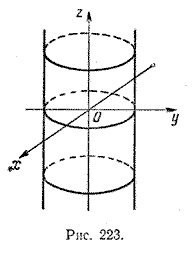
Полученное уравнение является уравнением искомой поверхности вращения, которая называется круговой конической поверхностью (рис. 224).

Задача 5. Составить уравнение поверхности вращения прямой 2х = 3у, z =0 вокруг оси Ох.

Из уравнения 3у = 2х, используя формулу (2), находим 9(y 2 + z 2 ) = 4x 2 . Это и есть искомое уравнение.

Видео:Объем тела, образованного вращением кривой вокруг оси хСкачать

Уравнение поверхности образованной вращением линии вокруг оси ох

3. О поверхностях второго порядка

3.1. Поверхности вращения в координатах

Пусть f ( х, у, z ) = 0 — уравнение с переменными х , y , z ; Ф — некоторая поверхность (на рис. 246 изображена часть этой поверхности). Из курса 10 класса известно, что уравнение f ( x, y, z ) = 0 называется уравнением поверхности Ф , если этому уравнению удовлетворяют координаты х , у, z любой точки М этой поверхности и не удовлетворяют координаты ни какой точки пространства, не принадлежащей поверхности Ф.

Если f ( x, y, z ) — многочлен, то его степень называют порядком поверхности Ф .

Мы знаем, например, что сфера с центром K ( a ; b ; с ) и радиусом R > 0 в декартовой прямоугольной системе координат Oxyz задаётся уравнением

( x – a ) 2 + ( y – b ) 2 + ( z – c ) 2 = R 2 .

Из этого уравнения следует, что сфера — поверхность второго порядка.

Заметим, что уравнение второго порядка может задавать «поверхность», состоящую из двух плоскостей. Например, уравнение ху + у 2 = 0 задаёт пару пересекающихся плоскостей, одна из которых имеет уравнение у = 0, другая — уравнение х + у = 0.

Eсли в пространстве некоторая линия γ является пересечением двух поверхностей Ф 1 и Ф 2 , заданных уравнениями f 1 ( x , y , z ) = 0 и f 2 ( х, у, z ) = 0, то координаты х, у, z любой точки М линии γ удовлетворяют каждому из этих уравнений, т. е. удовлетворяют системе уравнений

(1)

В этом случае говорят, что система уравнений (1) задаёт линию γ .

Разрешив уравнения этой системы относительно х и у (если это возможно), получим систему уравнений

(2)

равносильную системе (1), следовательно, задающую ту же самую линию γ .

Если линию γ вращать вокруг некоторой прямой m, то при этом вращении образуется некоторая поверхность Ф , которую называют поверхностью вращения, а прямую m — осью вращения или осью симметрии этой поверхности (вспомните сферическую и сегментную поверхности).

Для получения уравнения поверхности Ф достаточно выбрать на ней любую точку M ( X ; Y ; Z ) и выразить в координатной форме свойство, которым обладают только точки M ( X ; Y ; Z ) ∈ Ф ; в результате получим уравнение относительно X, Y, Z , которое и является искомым уравнением поверхности Ф .

Составим уравнение поверхности Ф , которая образуется вращением вокруг оси Oz линии γ , заданной системой уравнений (2). Для этого через произвольную точку M ( X ; Y ; Z ) ∈ Ф проведём плоскость, перпендикулярную оси Oz , т. е. плоскость z = Z (рис. 247). Эта плоскость пересекает поверхность Ф по окружности с центром K (0; 0; Z ) на оси вращения Oz , а линию γ — в некоторой точке Р ( х ; у ; z = Z ). Так как KМ = KР , то

X 2 + Y 2 = x 2 + y 2 . (3)

Учитывая, что z = Z , имеем для x и у в системе (2):

После подстановки этих значений x и у в уравнение (3) получаем искомое уравнение поверхности Ф с осью вращения Oz в виде:

X 2 + Y 2 = + . (4)

(Обратите внимание: правая часть уравнения (4) есть некоторая функция f переменной Z, т. е. f ( Z ) = + . )

Справедливо обратное утверждение: любое уравнение X 2 + Y 2 = f ( Z ) задаёт поверхность вращения с осью Oz , так как сечением этой поверхности плоскостью Z = α ( α = const) является окружность с центром на оси Oz .

Из сказанного следует: чтобы получить уравнение поверхности, которая образуется вращением вокруг оси Oz линии, заданной системой уравнений (1), достаточно выразить х и у через z , после чего сложить квадраты левых и правых частей полученных равенств.

Аналогично получаются уравнения поверхностей, образованных вращением линии вокруг осей Ох и Оу .

3.2. Поверхности вращения второго порядка

Рассмотрим некоторые поверхности, образованные вращением кривых второго порядка вокруг своих осей симметрии.

Пусть окружность радиуса R с центром в начале системы координат Oxyz , расположенная в плоскости Oyz (рис. 248, а ), задана системой уравнений:

Поверхностью, образованной вращением этой окружности вокруг оси Oz , является известная вам сфера ( сферическая поверхность ) (рис. 248, б ).

Уравнение этой сферы

x 2 + у 2 + z 2 = R 2 (5)

получим после сложения левых и правых частей равенств у 2 = r 2 – z 2 и x 2 = 0. Уравнение (5) называется каноническим ( простейшим ) уравнением сферы .

б) Эллипсоид вращения

Из планиметрии известно, что эллипсом называется множество всех точек М плоскости, для каждой из которых сумма расстояний до двух данных точек F 1 и F 2 той же плоскости, называемых фокусами , есть величина постоянная, большая, чем расстояние между фокусами (рис. 249, а ).

Эллипс с центром в начале координат и осями симметрии Ох и Оу задаётся каноническим уравнением: = 1 (где а и b — длины полуосей эллипса).

Пусть эллипс расположен в плоскости Oyz и задан системой уравнений:

(6)

Поверхность, образованная вращением эллипса вокруг его оси симметрии, называется эллипсоидом вращения .

Будем вращать эллипс, заданный системой уравнений (6), вокруг оси Oz . Чтобы получить уравнение образованного при этом эллипсоида вращения (рис. 249, б ), из первого уравнения системы (6) находим y 2 = a 2 . Тогда после сложения этого уравнения и уравнения х 2 = 0 и последующего преобразования получаем искомое уравнение

= 1, (6a)

которое называется каноническим уравнением эллипсоида вращения .

Из уравнения (6а) видно, что любая плоскость z = m ( m b ) , перпендикулярная оси вращения эллипсоида, пересекает его по окружности с центром (0; 0; m ) на оси Oz и радиусом

R = a .

в) Параболоид вращения

Из планиметрии известно, что параболой называется множество всех точек М плоскости, для каждой из которых расстояние до данной точки F , называемой фокусом , равно расстоянию до данной прямой а, называемой директрисой (рис. 250, а ) параболы.

Парабола с вершиной в начале системы координат Оху и осью симметрии Ох задаётся каноническим уравнением: у 2 = 2 рх, где р — расстояние между фокусом и директрисой. При 2 p = 1 парабола имеет уравнение y 2 = x.

Поверхность, образованная вращением параболы вокруг её оси симметрии, называется параболоидом вращения (рис. 250, б ). Вершина параболы при этом называется вершиной параболоида вращения.

Парабола, расположенная в координатной плоскости Oyz и имеющая своей вершиной начало координат, а осью симметрии — координатную ось Oz , может быть задана в декартовой прямоугольной системе координат Oxyz системой уравнений:

(7)

Будем вращать эту параболу вокруг оси Oz . Уравнение

образованного при этом параболоида вращения (рис. 250, б ) получим после почленного сложения уравнений

у 2 = z и х 2 = 0.

Уравнение (7а) называется каноническим уравнением параболоида вращения с осью вращения Oz. Из этого уравнения (7а) видно, что любая плоскость, перпендикулярная оси вращения (такая плоскость имеет уравнение z = m, m > 0), пересекает данный параболоид по окружности с центром (0; 0; m ) на оси Oz и радиусом R = .

г) Гиперболоиды вращения

Из планиметрии известно, что гиперболой называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек той же плоскости, называемых фокусами , есть величина постоянная, меньшая, чем расстояние между фокусами.

Гипербола с действительной осью Ох и мнимой осью Oy (рис. 251, а ) в системе координат Oxy задаётся каноническим уравнением: = 1.

Пусть гипербола расположена в координатной плоскости Oyz и задана системой уравнений:

(8)

Координатная ось Oy является действительной осью данной гиперболы, а координатная ось Oz — её мнимой осью.

Если вращать данную гиперболу вокруг её действительной оси (оси Оу ), то получим поверхность, состоящую из двух частей. Эти части называют полостями ( или полами ) , а полученная при этом поверхность называется двуполостным гиперболоидом вращения (рис. 251, б ).

Найдём уравнение этой поверхности.

Из уравнений (8) имеем:

После элементарных преобразований получаем искомое уравнение

= 1, (8а)

которое называется каноническим уравнением двуполостного гиперболоида вращения с осью Оу .

Вращая ту же самую гиперболу вокруг её мнимой оси (т. е. вокруг оси Oz ), получим поверхность, которая называется однополостным гиперболоидом вращения (рис. 252, а ). Рассуждениями, аналогичными предыдущим, получаем каноническое уравнение этого гиперболоида в виде

= 1. (8б)

Любая плоскость z = m , перпендикулярная оси вращения однополостного гиперболоида (рис. 252, б ), пересекает этот гиперболоид по окружности с центром (0; 0; m ) на оси Oz и радиусом R = . Из выражения для вычисления радиуса окружности — сечения видно, что самым «узким» сечением нашего гиперболоида является окружность радиуса а. Эта окружность получается при пересечении данного гиперболоида плоскостью z = 0 и называется горловой окружностью (или горловиной ) однополостного гиперболоида.

Если вращать вокруг оси Oz прямую

(8в)

(эта прямая лежит в плоскости х = а и не параллельна оси Oz , см. рис. 252, б ), то при этом вращении образуется тот же однополостный гиперболоид.

В самом деле, из уравнений (8в) имеем:

После почленного сложения уравнений этой системы и последующего преобразования полученного уравнения приходим к уравнению

= 1,

совпадающему с уравнением (8б), следовательно, задающего тот же самый однополостный гиперболоид.

Но если вращать вокруг оси Oz прямую, заданную системой уравнений

(8г)

(эта прямая также лежит в плоскости х = а и не параллельна оси Oz , см. рис. 252, б ), то при этом вращении вновь образуется однополостный гиперболоид, заданный уравнением (8б).

Поверхность, образованную движением прямой, называют линейчатой поверхностью, а прямые, целиком лежащие на этой поверхности, называют её прямолинейными образующими.

Из сказанногo следует, что однополостный гиперболоид является линейчатой поверхностью . При этом: множество всех прямых, образованное движением прямой (8в), представляет собой одну серию прямолинейных образующих однополостного гиперболоида (8б) ( «полуквадрику» ) , а множество всех прямых, образованное движением прямой (8г), — другую серию прямолинейных образующих этого гиперболоида (вторую «полуквадрику» ) .

Примечательным является тот факт, что любые две образующие разных серий однополостного гиперболоида пересекаются, а любые две его образующие одной серии скрещиваются (рис. 253).

д) Коническая поверхность вращения

Пусть кривая второго порядка состоит из двух пересекающихся в начале координат прямых, расположенных в плоскости Oyz (рис. 254, а ), и задана системой уравнений

(9)

Если эту пару пересекающихся прямых вращать вокруг оси Oz , то получим поверхность, которая состоит из двух частей, называемых полостями ( или полами ) , а сама поверхность называется конической поверхностью вращения (рис. 254, б ). Иногда эту поверхность в целях краткости называют простo конусом вращения .

Из определения конической поверхности следует, что она является линейчатой поверхностью.

Рис. 254

Чтобы получить уравнение этой конической поверхности, находим:

После почленного сложения уравнений системы и последующего преобразования полученного уравнения приходим к уравнению:

= 0, (9a)

которое называется каноническим уравнением конической поверхности вращения с осью вращения Oz .

Ecли жe вращать ту же пару прямых вокруг оси Оy (которая также является их осью симметрии), то получим вновь коническую поверхность вращения, но её каноническое уравнение имеет другой вид, а именно:

= 0. (9б)

Обратите внимание! Правая часть канонического уравнения конической поверхности равна нулю, а знак «–» в левой части уравнения «указывает» на ось вращения этой поверхности.

е) Цилиндрическая поверхность вращения

Пусть кривая второго порядка состоит из двух параллельных прямых, лежащих в плоскости Oyz (рис. 255, а ), и задана системой уравнений

(10)

Если эту пару параллельных прямых вращать вокруг оси

Oz координатная ось Oz является осью симметрии прямых и на которые распадается кривая второго порядка то получим поверхность, которая называется цилиндрической поверхностью враще ния (рис. 255, б ). Иногда эту поверхность в целях краткости называют просто цилиндром вращения .

Из определения цилиндрической поверхности следует, что она является линейчатой поверхностью.

После почленного сложения уравнений системы получаем искомое уравнение этой поверхности

x 2 + y 2 = a 2 , (10а)

которое называется каноническим уравнением цилиндрической поверхности вращения с осью вращения Oz.

Если эту же пару параллельных прямых вращать вокруг оси Оу , то получим поверхность второго порядка, состоящую из двух параллельных плоскостей (рис. 256) (иногда говорят, распавшуюся на две параллельные плоскости). Их уравнение имеет вид

Уравнение (11) нельзя получить из уравнений (10) по правилу, установленному в п. 1 «Дополнений», так как из этих уравнений у не выражается как функция z .

Цилиндрическую поверхность вращения с осью вращения Oz , заданную уравнением (10а), можно получить непрерывным движением прямой, параллельной оси Oz и пересекающей расположенную в плоскости Оху окружность Эта окружность называется направляющей цилиндрической поверхности.

Таким же образом можно получить другие цилиндрические поверхности. К ним относятся:

— эллиптический цилиндр , направляющей которого служит эллипс. Если образующие эллиптического цилиндра параллельны оси Oz , то его каноническое уравнение имеет вид:

= 1. (12)

Изображение этого цилиндра совпадает с изображением цилиндра вращения (см. рис. 255, б );

— параболический цилиндр , направляющей которого служит парабола. Если образующие параболического цилиндра параллельны оси Oz , а парабола расположена в плоскости Оху (рис. 257), то такой цилиндр может быть задан уравнением:

— гиперболический цилиндр , направляющей которого служит гипербола. Если образующие гиперболического цилиндра параллельны оси Оz, а гипербола расположена в плоскости Оху (рис. 258), то он может быть задан уравнением:

= 1. (14)

Рис. 258

Мы получили только канонические ( простейшие ) уравнения каждой из рассмотренных выше поверхностей второго порядка. Такие уравнения имеют рассмотренные поверхности вследствие частного, наиболее «удобного», их расположения относительно системы координат Oxyz . Но если, например, сфера радиуса R = 4 имеет своим центром не начало координат, а точку А (2; –3; –1), то эта сфера задаётся уравнением

( х – 2) 2 + ( у + 3) 2 + ( z + 1) 2 = 16,

которое после раскрытия скобок приводится также к уравнению второго порядка

x 2 + y 2 + z 2 – 4 х + 6 у + 2 z + 2 = 0.

В этом уравнении сферы число членов больше, чем в каноническом её уравнении (5). Аналогично, каждая из рассмотренных выше поверхностей второго порядка — эллипсоид, параболоид, гиперболоиды, цилиндр и конус, будучи расположенной общим образом относительно системы координат Oxyz , может быть задана общим уравнением второго порядка относительно переменных х, у, z . Поэтому вводится такое определение.

Поверхностью второго порядка называется множество всех точек М ( x ; y ; z ) пространства, координаты x, y, z которых удовлетворяют уравнению

a 11 x 2 + a 22 y 2 + a 33 z 2 + 2 a 12 xy + 2 a 13 xz + 2 a 23 yz + 2 a 14 x +
+ 2 a 24 y + 2 a 34 z + a 44 = 0.

Это уравнение называется общим уравнением поверхности второго порядка ( коэффициенты a 11 , a 22 , a 33 , a 12 , a 13 , a 23 одновременно не равны нулю ) . Тaк кaк поверхности второго порядка задаются квадратными уравнениями, то эти поверхности кратко называют квадриками.

3.3. Линии второго порядка как плоские сечения конической поверхности

Пусть дана коническая поверхность вращения с вершиной в точке S и осью вращения a . Из определения конической поверхности следует, что любая плоскость, проходящая через вершину S и ось а конической поверхности, пересекает эту поверхность по двум её линейным образующим (рис. 259, а ), т. е. по кривой второго порядка, распавшейся на две пересекающиеся прямые.

Мы рассмотрим вопрос о пересечении конической поверхности вращения и любой плоскости, не проходящей через вершину этой поверхности. Из определения конической поверхности вращения следует, что любая плоскость, не проходящая через вершину S и перпендикулярная оси вращения a , пересекает эту коническую поверхность по окружности (рис. 259, б ) .

Далее мы рассмотрим три принципиально различных возможных расположения секущей плоскости α по отношению к конической поверхности вращения.

а) Плоскость α пересекает все линейные образующие конической поверхности и не перпендикулярна оси вращения а (рис. 260) . Докажем, что полученная при этом в сечении конической поверхности кривая l является эллипсом.

Рис. 260

Проведём через ось а плоскость, перпендикулярную секущей плоскости α ; она пересекает поверхность по двум прямолинейным образующим. Будем считать полученные образующие лежащими в плоскости чертежа, а точки их пересечения с плоскостью α обозначим через R и Т .

Впишем в угол, образованный этими образующими, две окружности, касающиеся прямой RT . Центры этих окружностей лежат на оси конической поверхности. Пусть одна из окружностей касается прямой RT в точке F 1 и линейных образующих в точках Р и Q , а вторая касается прямой RT в точке F 2 и линейных образующих — в точках P ′ и Q ′ . При вращении этих окружностей вокруг оси конической поверхности образуются две сферы (I и II), вписанные в эту коническую поверхность (в одну её полость). Сфера I касается конической поверхности по окружности PQ , а сфера II — по окружности Р ′ Q ′ , которые лежат в параллельных между собой и перпендикулярных оси вращения а плоскостях. Для обеих сфер плоскость α является общей касательной плоскостью с точками касания соответственно F 1 и F 2 .

Проведём теперь через любую точку M линии l прямолинейную образующую SM конической поверхности, и точки пересечения этой образующей с окружностями PQ и Р ′ Q ′ обозначим соответственно А и В. Далее соединим отрезками точку М с точками F 1 и F 2 . Тогда:

| MA | = | MF 1 | (как отрезки касательных прямых, проведённых из точки М к сфере I);

| МВ | = | MF 2 | (как отрезки касательных прямых, проведённых из точки М к сфере II).

Получаем: | MF 1 | + | MF 2 | = | MA | + | MB | = | AB |.

Так как плоскости окружностей PQ и P ′ Q ′ перпендикулярны оси вращения конической поверхности, то длина отрезка AB постоянна для любой линейной образующей, т. е. не зависит от выбора точки M на кривой l. Это означает, что для любой точки M линии l сумма расстояний | MF 1 | и | MF 2 | до двух данных точек F 1 и F 2 есть величина постоянная, откуда, в свою очередь, следует, что кривая l — эллипс, что и требовалось доказать. ▼

б) Рассмотрим теперь случай, когда плоскость параллельна двум линейным образующим конической поверхности вращения.

В этом случае плоскость α пересекает обе полости конической поверхности (рис. 261), и в сечении получается линия l , состоящая, по-видимому, из двух ветвей. Интуитивно можно предположить, что этой линией окажется гипербола. Докажем, что это действительно так.

Как и в предыдущем случае, проведём через ось а плоскость, перпендикулярную секущей плоскости α ; она пересекает коническую поверхность по двум прямолинейным образующим. Будем считать полученные образующие лежащими в плоскости чертежа.

Впишем в различные полости конической поверхности две сферы (обозначим их опять I и II) так, чтобы они касались секущей плоскости α в некоторых точках F 1 и F 2 . Пусть Р и Q — точки касания сферы I с прямолинейными образующими, лежащими в плоскости чертежа, а Р ′ и Q ′ — точки касания сферы II с этими образующими. Тогда сфера I касается конической поверхности по окружности PQ , а сфера II — по окружности Р ′ Q ′ , которые лежат в параллельных между собой и перпендикулярных оси вращения а плоскостях.

Проведём теперь через любую точку М линии l прямолинейную образующую SM конической поверхности, и точки пересечения этой образующей с окружностями PQ и P ′ Q ′ обозначим соответственно А и В. Соединив отрезками точку М с точками F 1 и F 2 , имеем:

| МA | = | MF 1 | (как отрезки касательных прямых, проведённых из точки М к сфере I);

| MB | = | MF 2 | (как отрезки касательных прямых, проведённых из точки М к сфере II).

|| m F 2 | – | m F 1 || = || МВ | – | МА || = | AB |.

Так как плоскости окружностей РQ и P ′ Q ′ перпендикулярны оси вращения конической поверхности, то длина отрезка AВ , расположенного на образующей конуса, постоянна для любой его образующей, т. е. не зависит от выбора точки М на линии l . Это означает, что для любой точки М линии l модуль разности расстояний | MF 2 | и | MF 1 | до двух данных точек F 1 и F 2 есть величина постоянная, следовательно, кривая l — гипербола, что и требовалось доказать. ▼

в) Рассмотрим третий случай, когда секущая плоскость α , параллельна одной из образующих (обозначим её SX ) конической поверхности вращения (рис. 262). В этом случае плоскость α перпендикулярна плоскости, проходящей через образующую SX и ось a конуса, а линия l пересечения плоскости α и конической поверхности состоит из одной ветви, простирающейся в бесконечность. Покажем, что эта линия является параболой.

Рис. 262

Впишем в коническую поверхность сферу, касающуюся плоскости α в некоторой точке F . Плоскость β , содержащая окружность ω соприкосновения этой сферы и конической поверхности, перпендикулярна оси a конуса и пересекает плоскость α по прямой KL .

Проведём через любую точку М линии l образующую конической поверхности и обозначим через Р точку её касания со сферой (точка P лежит на окружности ω ). Тогда | MF | = | МР | (как отрезки касательных к сфере, проведённых из точки M ). Далее проведём плоскость δ через точку М параллельно плоскости β , в которой лежит окружность ω , и обозначим точки пересечения данной образующей SX с плоскостями β и δ соответственно А и B ( А = SX ∩ ω ) . Тогда | АВ | = | MP | (как длины отрезков образующих конической поверхности, заключённых между плоскостями, перпендикулярными к оси этой поверхности). Плоскость, проходящая через образующую SX перпендикулярно плоскости α , пересекает эту плоскость по прямой DE , параллельной АВ и перпендикулярной прямой KL . Причём | DE | = | АВ | (как отрезки параллельных прямых, заключённые между параллельными плоскостями). Eсли теперь провести в плоскости α перпендикуляр МC из точки М на прямую KL , то он будет параллелен и равен DE : | MC | = | DE |. Тогда получаем:

| MC | = | DE | = | AB | = | MP |.

Учитывая, что | MF | = | МР | , приходим к выводу: | MF | = | МС |. Из этого равенства следует, что точка М независимо от её положения на линии l одинаково удалена от точки F и от прямой KL , следовательно, линия l является параболой, что и требовалось доказать. ▼

На рисунке 263 изображены все возможные виды плоских сечений конической поверхности.

Таким образом, изученные вами в планиметрии кривые второго порядка являются различными плоскими сечениями конической поверхности вращения, поэтому их называют коническими сечениями , а для краткости — просто кониками . При этом окружность, эллипс, гиперболу и параболу называют собственными или невырожденными коническими сечениями ( невырожденными кониками ) . Они обладают многими интересными и красивыми свойствами, о которых вы узнаете в высшей школе.

Видео:§64 Поверхности вращенияСкачать

Поверхности вращения

Дата добавления: 2015-08-14 ; просмотров: 4640 ; Нарушение авторских прав

Поверхностью вращения называется множество точек,которое образуется при вращении некоторой плоской линии l вокруг оси.

Линия l называется меридианом поверхности вращения, а ось — её осью вращения. Отметим, что при вращении меридиана вокруг оси каждая его точка описывает окружность.

Рассмотрим поверхность, полученную вращением линии l вокруг оси Oz. Пусть линия l расположена в плоскости OYZ и задана уравнениями:

Уравнение вращающейся линии надо преобразовать так, чтобы оно стало уравнением поверхности вращения.

Пусть М(x; y; z) — произвольная точка поверхности. Через точку М проведем плоскость, перпендикулярную оси Oz; эта плоскость пересечет поверхность по окружности с центром в точке О` на оси Oz: O`(0; 0; z). Обозначим буквой N точку пересечения указанной окружности и линии l. Точка N имеет координаты (0; Y; Z). (Рис.8.6.)

Поскольку длины отрезков (O`N) и (O`M) равны между собой (как радиусы одной и той же окружности), т.е. и то .

Т.к. точка , то отсюда (8.3.)

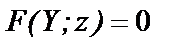
Итак, координаты произвольной точки M(x; y; z), принадлежащей поверхности вращения, удовлетворяют уравнению (8.3.).

Уравнение (8.3.) и является уравнением поверхности вращения(поверхность полученная вращением линии l, лежащей в плоскости Ozy, вокруг оси Oz).

Замечание: Уравнение (8.3.) поверхности вращения получается из уравнения линии l в результате следующих формальных действий: заменяют «y» на « ».

Аналогично, если ту же линию l вращать вокруг оси Oy, то полученная поверхность вращения будет иметь уравнение .

Если линия l лежит в плоскости Oxy и задана уравнениями то уравнения поверхностей, полученных от вращения l вокруг осей x или y, имеют соответственно вид: или .

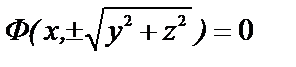
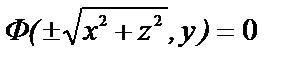
Пример 8.3.1. Составить уравнение поверхности, образованной вращением гиперболы вокруг оси Ох.

Решение:

Пример 8.3.2. Окружность радиуса r вращается около прямой l, лежащей в той же плоскости, что и окружность, и отстоящей от центра С последней на расстоянии R. Составить уравнение поверхности вращения, при условии, что R > r.

Решение: Примем плоскость окружности за плоскость ху, ось вращения — за ось у. С(R,0).

Уравнение окружности:

Уравнение поверхности вращения:

или , — поверхность 4-го порядка.

Замечание. Если R > r, то эта поверхность называется шаром.

8.4. Поверхности второго порядка заданные каноническими уравнениями

Будем рассматривать различные поверхности второго порядка, заданные каноническими уравнениями. Чтобы судить о форме этих поверхностей по виду их уравнений, будем использовать так называемый метод сечений.

Сущность метода сечений состоит в том, что рассматриваются линии пересечения данной поверхности с различными плоскостями.

Во многих случаях полезно рассекать поверхность плоскостями параллельными одной из координатных плоскостей, или плоскостями координат.

Зная ряд сечений, получаем представление о самой поверхности.