Уравнение поверхностей уровня для скалярного поля (3 видео)

Скалярное поле. Векторное поле. Основные понятия и задачи

Содержание

Понятие поля в математике
Скалярное поле: определение, поверхности уровня и линии уровня
Векторное поле: определение, векторные линии
Поверхности и линии уровня скалярного поля
Поверхности и линии уровня
Векторный анализ
Скалярное поле
Векторный анализ
📹 Видео

Видео:Поверхности уровня скалярного поляСкачать

Понятие поля в математике

Теория поля является разделом математики, однако понятие поля лежит в основе многих представлений современной физики. В общем случае говорят, что в пространстве задано поле некоторой величины u , если в каждой точке пространства (или некоторой его части) определено значение этой величины. Так, например, при изучении потока газа приходится исследовать несколько полей: температурное поле (в каждой точке температура имеет определённое значение), поле давлений, поле скоростей и другие поля.

Поле величины u называется стационарным, (или установившимся), если u не зависит от времени t . В противном случае поле называется нестационарным (или неустановившимся). Таким образом, величина u есть функция точки M и времени t .

В задачах физики чаще всего приходится иметь дело со скалярными и векторными величинами. В соответствии с этим различают два вида полей: скалярные и векторные.

Видео:Поверхности и линии уровняСкачать

Скалярное поле: определение, поверхности уровня и линии уровня

Пусть D — некоторая область на плоскости или в пространстве.

Определение скалярного поля. Если в области D каждой точке M(x,y,z) пространства или точке M(x,y) плоскости в каждый момент времени t по определённому закону ставится в соответствие значение скалярной величины u , то функция u(x,y,z,t) в случае пространства или u(x,y,t) в случае плоскости называется скалярным полем.

Понятия скалярного поля и функции, определённой в области D , совпадают.

Примером скалярного поля может служить поле температур воздуха в некотором помещении, если температуру рассматривать как функцию точки. В точках, расположенных ближе к источнику тепла, температура выше, чем в точках, расположенных дальше от источника тепла. Можно привести и такие примеры, как поле освещённости, поле плотности массы и тому подобные.

Для получения более полного представления о скалярном поле используется его графическое изображение — поверхности уровня в пространстве и линии уровня на плоскости.

Линии уровня широко используются при составлении топографических и метеорологических карт. На топографических картах линия уровня — линия, в точках которой отмечена одна и та же высота над уровнем моря. На метеорологических картах строят два вида линий уровня — изотермы (линии одинаковой температуры) и изобары (линии одинакового давления).

Определение. Поверхностью уровня скалярного поля называется множество всех тех точек пространства, в которых скалярное поле постоянно.

Уравнение поверхности уровня скалярного поля u(x,y,z) :

При постоянном изменении значения C поверхности уровня заполняют всю область пространства. Если поверхности уровня размещены плотно, скалярное поле изменяется быстро. Если же поверхности уровня расположены редко, скалярное поле изменяется медленно.

Определение. Линией уровня скалярного поля называется множество всех тех точек на плоскости, в которых скалярное поле постоянно.

Уравнение линии уровня скалярного поля u(x,y) :

Пример 1. Определить поверхности уровня скалярного поля и их вид.

Решение. Уравнением поверхностей уровня данного скалярного поля является

Поверхностями уровня являются конусы с вершиной в начале координат и осью вращения Oy . Так как по области определения , то одновременно не может быть x = 0 и z = 0 . Поэтому следует исключить вершину конусов.

Пример 2. Определить линии уровня скалярного поля и их вид.

Решение. Уравнением линий уровня данного скалярного поля является

Из этого уравнения выразим «игрек»:

Так как arcsinC — также константа, обозначим её C 1 . Тогда

Графиками этих линий являются параболы с вершиной в точках и ветвями вниз. На рисунке изображены линии уровня в трёх случаях: C 1 = 1 — красная линия, C 1 = 2 — зелёная линия, C 1 = 3 — синяя линия.

Видео:Построить поверхности уровня и линии уровня скалярного поляСкачать

Векторное поле: определение, векторные линии

Понятие векторного поля во многом аналогично понятию скалярного поля.

Определение векторного поля. Если в некоторой области пространства каждой точке M по определённому закону ставится в соответствие вектор , то векторная функция называется полем вектора или векторным полем.

Таким образом, векторным полем является векторная функция точки пространства

Примерами векторного поля являются поля скорости и ускорения в текущей жидкости или газе, поле силы гравитации, поле интенсивности электростатического поля и тому подобные. Вообще, примером векторного поля может служить поле сил любой природы.

Мы будем рассматривать только стационарные векторные поля, то есть поля, не зависящие от времени.

Проекции вектора , соответствующего точке M , на координатные оси обозначим P = P(x,y,z) , Q = Q(x,y,z) , R = R(x,y,z) . Тогда векторное поле сможем задать через компоненты:

Таким образом, векторное поле можно определить тремя скалярными функциями P , Q , R . Пусть эти функции и их частные производные по переменным x,y,z являются непрерывными функциями.

Определение. Векторной линией называется линия, направление которой в каждой точке касательной совпадает с направлением вектора поля в этой точке (рисунок ниже).

Векторные линии поля силы обычно называют линиями силы, векторные линии поля скоростей потока жидкости или газа — векторами потока. У стационарного потока жидкости линии потока совпадают с траекториями частиц жидкости.

Уравнения векторных линий можно найти, решив систему дифференциальных уравнений

Пример 3. Найти линии вектора поля .

Решение. Так как , , , получаем систему дифференциальных уравнений

Из первого равенства получаем

где . Из последнего равенства следует . Таким образом, получаем

И получаем уравнения векторных линий данного векторного поля:

Видео:Градиент скалярного поляСкачать

Поверхности и линии уровня скалярного поля

Поверхности и линии уровня

Рассмотрим скалярное поле, задаваемое функцией 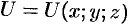. Для наглядного представления скалярного поля используют поверхности и линии уровня.

Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция 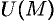принимает постоянное значение, т. е.

Давая в уравнении (70.1) величине с различные значения, получим различные поверхности уровня, которые в совокупности как бы расслаивают поле. Через каждую точку поля проходит только одна поверхность уровня. Ее уравнение можно найти путем подстановки координат точки в уравнение (70.1).

Для скалярного поля, образованного функцией

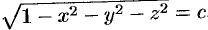
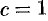
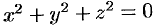
поверхностями уровня является множество концентрических сфер с центрами в начале координат: . В частности, при получим , т. е. сфера стягивается в точку.

Для равномерно раскаленной нити поверхности уровня температурного поля (изотермические поверхности) представляют собой, круговые цилиндры, общей осью которых служит нить.

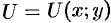
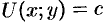
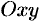
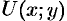
В случае плоского поля равенство представляет собой уравнение линии уровня поля, т. е. линия уровня — это линия на плоскости , в точках которой функция сохраняет постоянное значение.

В метеорологии, например, сети изобар и изотерм (линии одинаковых средних давлений и одинаковых средних температур) являются линиями уровня и представляют собой функции координат точек местности.

Линии уровня применяются в математике при исследовании поверхностей методом сечений (см. п. 12.9).

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

Другие темы по высшей математике возможно вам они будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Скалярное и векторное поля. Определения и отличия.Скачать

Векторный анализ

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Если в каждой точке пространства или части пространства определено значение некоторой величины, то говорят, что задано поле данной величины. Поле называется скалярным, если рассматриваемая величина скалярна, т.е. вполне характеризуется своим числовым значением. Например, поле температур.

Скалярное поле

Скалярное поле задается скалярной функцией точки и = /(М). Если в пространстве введена декартова с истема координат, то и есть функция трех переменных х, yt z — координат точки М: Определение. Поверхностью уровня скалярного поля называется множество точек, в которых функция f(M) принимает одно и то же значение. Уравнение поверхности уровня Пример 1. Найти поверхности уровня скалярного поля ВЕКТОРНЫЙ АНАЛИЗ Скалярное поле Поверхности и линии уровня Производная по направлению.

Производная Градиент скалярного поля Основные свойства градиента Инвариантное определение градиента Правила вычисления градиента -4 Согласно определению уравнением поверхности уровня будет . Это уравнение сферы (с Ф 0) с центром в начале координат. Скалярное поле называется плоским, если во всех плоскостях, параллельных некоторой плоскости, поле одно и то же.

Если указанную плоскость принять за плоскость хОу, то функция поля не будет зависеть от координаты z, т. е. будет функцией только аргументов х и у, Плоское поле можно характеризовать помощьюлиний уровня — множестваточек плоскости, в которых функция /(ж, у) имеетодно и тоже значение. Уравнение линии уровня — Пример 2.

Найти линии уровня скалярного поля Линии уровня задаются уравнениями При с = 0 получаем пару прямых получаем семейство гипербол (рис. 1). 1.1. Производная по направлению Пусть имеется скалярное поле, определяемое скалярной функцией и = /(Af). Возьмем точку Afo и выберем направление, определяемое вектором I. Возьмем другую точку М так, чтобы вектор М0М был параллелен вектору 1 (рис. 2). Обозначим длину вектора МоМ через А/, а приращение функции /(Af) — /(Afo), соответствующее перемещению Д1, через Ди.

Отношение определяет среднюю скорость изменения скалярного поля на единицу длины поданному направлению Пусть теперь стремится к нулю так, чтобы вектор М0М все время оставался параллельным вектору I. Определение. Если при Д/ О существует конечный предел отношения (5), то его называют производной функции в данной точке Afo поданному направлению I и обозначают символом зг!^ . Так что, по определению, Это определение не связано с выбором системы координат, т. е. носит**вариантный характер.

Найдем выражение для производной по направлению в декартовой системе координат. Пусть функция / дифференцируема в точке . Рассмотрим значение /(Af) в точке . Тогда полное приращение функции можно записать в следующем виде: где а символы означают, что частные производные вычислены в точке Afo. Отсюда Здесь величины jfi, , ^ суть направляющие косинусы вектора . Так как векторы МоМ и I сонаправлены , то их направляющие косинусы одинаковы:

Так как M Afo, осгавая сь все время на прямой, параллельной вектору 1, то углы постоянные потому Окончательно из равенств (7) и (8) получаем Эамуан ис 1. Частные производные , являются производными функции и по направлениям координатныхосей ссчлвешне нно- Пример 3. Найти производную функции по направлению к точке Вектор имеет длину .

Его направляющие косинусы: По формуле (9) будем иметь Тот факт, что , означает, что скалярное поле в точке в данном направлении возраста- Для плоского поля производная по направлению I в точке вычисляется по формуле где а — угол, образованный вектором I с осью Ох. Зммчмм 2. Формула (9) для вычисления производной по направлению I в данной точке Afo остается в силе и тогда, когда точка М стремится к точке Мо по кривой, для которой вектор I является касательным в точке ПрИШр 4.

Вычислить производную скалярного поля в точке Afo(l, 1). принадлежащей параболе по направлению этой кривой (в направлении возрастания абсциссы). Направлением ] параболы в точке считается направление касательной к параболе в этой точке (рис.3). Пусть касательная к параболе в точке Afo образует с осью Ох угол о.

Тогда откуда направляющие косинусы касательной Вычислим значения и в точке . Имеем Теперь по формуле (10) получаем.

Найти производную скалярного поля в точке по направлению окружности Векторное уравнение окружности имеет вид . Находим единичный вектор т касательной к окружности Точке соответствует значение параметра Значение г в точке Afo будет равно Отсюда получаем направляющие косинусы касательной к окружности в точке Вычислим значения частных производных данного скалярного поля в точке Значит, искомая производная .

Возможно вам будут полезны данные страницы:

Градиент скалярного поля Пусть скалярное поле определяется скалярной функцией которая предполагается дифференцируемой. Определение. Градиентом скалярного поля » в данной точке М называется вектор, обозначаемый символом grad и и определяемый равенством Ясно, что этот вектор зависиткак от функции /, так и отточки М, в которой вычисляется ее производная.

Пусгь 1 — единичный вектор в направлении Тогда формулу дл я производной по направлению можно записать в следующем виде: . тем самым производная от функ ии и по направлению 1 равна скалярному произведению градиента функ ии и(М) на орт 1° направления I. 2.1. Основные свойства градиента Теорема 1.

Градиент скалярного поля перпендикулярен к поверхности уровня (или к линии уровня, если поле плоское). (2) Проведем через произвольную точку М поверхность уровня и = const и выберем на этой поверхности гладкую кривую L, проходящую через точку М (рис. 4). Пусть I — векгор, касательный к кривой L в точке М. Так как на поверхности уровня и(М) = и(М|) для любой точки Мj е L, то С другой стороны, = (gradu, 1°). Поэтому .

Это означает, что векторы grad и и 1° ортогональны, Итак, векгор grad и ортогонален к любой касательной к поверхности уровня в точке М. Тем самым он ортогонален к самой поверхности уровня в точке М. Теорема 2. Градиент направлен в сторону возрастания функции поля. Ранее мы доказали, что градиент скалярного поля направлен по нормали к поверхности уровня, которая может быть ориентирована либо в сторону возрастания функции и(М), либо в сторону ее убывания.

Векторный анализ

Обозначим через п нормальк поверхности уровня, ориентированную в сторону возрастания функции ti(M), и найдем производную функции и в направлении этой нормали (рис. 5). Имеем Так как по условию рис.5 и поэтому ВЕКТОРНЫЙ АНАЛИЗ Скалярное поле Поверхности и линии уровня Производная по направлению Производная Градиент скалярного поля Основные свойства градиента Инвариантное определение градиента Правила вычисления градиента Отсюда следует, что grad и направлен в ту же сторону, что и выбранная нами нормаль п, т. е. в сторону возрастания функции и(М).

Теорема 3. Длина градиента равна наибольшей производной по направлению в данной точке поля, (здесь шах $ берется по всевозможным направлениям в данной точке М паю). Имеем где — угол между векторами 1 и grad п. Так как наибольшее значени Пример 1. Найти направление наибольшего иэмонония скалярного поля в точке а также величину этого наибольшего изменения в указанной точке. Направление наибольшего изменения скалярного поля указывается вектором .

Имеем так что Этот вектор определяет направление наибольшего возрастания поля в точко . Величина наибольшого изменения поля в этой точке равна 2.2. Инвариантное определение градиента Величины, характеризующие свойства изучаемого объекта и не зависящие от выбора системы координат, называются инвариантами данного объекта.

Например, длина кривой — инвариант этой кривой, а угол касательной к кривой с осью Ох — не инвариант. Основываясь на доказанных выше трех свойствах градиента скалярного поля, можно дать следующее инвариантное определение градиента. Определение. Градиент скалярного поля есть вектор, направленный по нормали к поверхности уровня в сторону возрастания функции поля и имеющий длину, равную наибольшей производной по направлению (в данной точке).

Пусть — единичный вектор

нормали, направленный в сторону возрастания поля. Тогда Пример 2. Найти градиент расстояния — некоторая фиксированная точка, a M(x,y,z) — текущая. 4 Имеем где — единичный вектор направления . Правила вычисления градиента где с — постоянное число. Приведенные формулы получаются непосредственно из определения градиента и свойств производных.

По правилу дифференцирования произведения Доказательство аналогично доказательству свойства Пусть F(и) — дифференцируемая скалярная функция. Тогда 4 По определению фадиента имеем Применим ко всем слагаемым правой части правило дифференцирования сложной функции. Получим В частности, Формула (6) следует из формулы Пример 3. Майти производную по направлению радиус-воктора г от функции По формуле (3) а по формуле В результате получим, что Пример 4.

Пусть дано плоское скалярное поле — расстояния от некоторой точки плоскости до двух фиксированных точек этой плоскости. Рассмотрим произвольный эллипс с фокусами Fj и F] и докажем, что всякий луч свота, вышедший из одного фокуса эллипса, после отражения от эллипса попадает в другой его фокус. Линии уровня функции (7) суть ВЕКТОРНЫЙ АНАЛИЗ Скалярное поле Поверхности и линии уровня Производная по направлению.

Производная Градиент скалярного поля Основные свойства градиента Инвариантное определение градиента Правила вычисления градиента Уравнения (8) описывают семейство эллипсов с фокусами в точках F) и Fj. Согласно результату примера 2 имеем Тем самым градиент заданного поля равен вектору PQ диагонали ромба, построенного на ортах г? и радиус-векторов. проведенных к точке Р(х, у) из фокусов F| и Fj, и значит, лежит на биссектрисе угла можду этими радиус-векторами (рис. 6).

По тооромо 1 градиент PQ перпендикулярен к эллипсу (8) в точке. Следова- Рис.6 тельно. нормаль к эллипсу (8) в любой ого точке делит пополам угол между радиус-векторами, проведенными в эту точку. Отсюда и из того, что угол падения равон углу отражения, получаем: луч света, вышедший из одного фокуса эллипса, отразившись от него, непременно попадает в другой фокус этого эллипса.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.