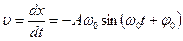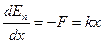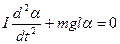Уравнение потенциальной энергии гармонических колебаний

Лекция 5. Механические колебания

План лекции

5.1. Основные характеристики колебательного движения.

5.2. Кинетическая, потенциальная и полная энергии гармонических колебаний.

5.3. Уравнение гармонических колебаний. Маятники.

5.4. Затухание колебания.

5.5. Вынужденные колебания. Резонанс.

5.6. Явление резонанса в строительстве.

Основные характеристики колебательного движения

Процессы точно или приблизительно повторяющиеся через одинаковые промежутки времени называются колебаниями.В зависимости от физической природы различают механические, электромагнитные и другие виды колебаний. Несмотря на разную природу колебаний, в них обнаруживаются одни и те же физические закономерности, они описываются одними и теми же математическими уравнениями и исследуются общими методами, разработка и применение которых составляют задачу теории колебаний.

В данном курсе физики мы будем изучать два наиболее распространенных класса колебаний: механические и электрические.

Среди разнообразных колебаний основную и существенную роль играют так называемые гармонические колебания, то есть такие, при которых колеблющаяся величина изменяется с течением времени по закону синуса или косинуса.

Рассмотрим гармонические колебания на примере колеблющейся точки.

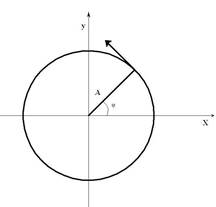
Пусть точка вращается по окружности радиуса А с угловой скоростью ω₀ (рис.5.1).

Рис.5.1.

Если точку спроецировать на оси X и Y, то ее проекции будут совершать колебания и удовлетворяют следующим уравнениям соответственно

, (5.1)

и (5.2)

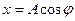
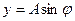
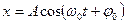
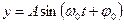
где х и y – смещения колеблющейся точки от положения равновесия;

А – амплитуда колебания (максимальное смещение);

ω₀ – круговая (циклическая) частота колебаний.

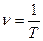
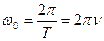
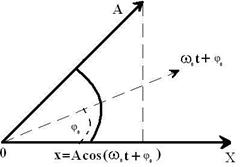
Точка совершает одно полное колебание за время Τ, называемое периодом колебания. Частота колебаний ν (число колебаний в единицу времени) есть . Между указанными величинами существует взаимосвязь

(5.3)

Геометрический смысл параметров уравнений (5.2) можно объяснить с помощью векторных диаграмм. Выберем на оси Х точку О и из этой точки под углом φ₀ проведем вектор А. Будем вращать вектор А с угловой скоростью ω₀ и тогда его проекция на ось будет смещаться на величину x (рис. 5.2).

Рис.5.2.

Колеблющаяся точка обладает скоростью и ускорением. Скорость материальной точки

(5.4)

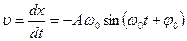
Ускорение материальной точки

(5.5)

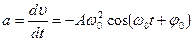
С учетом формулы (5.2) получим

(5.6)

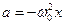
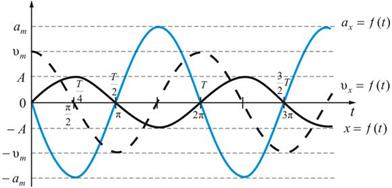
Сравнивая уравнения (5.2), (5.4) и (5.5) замечаем, что скорость опережает смещение на π/2. Фазы ускорения и смещения различаются на π (изменяются в противофазе). Графические зависимости смещения, скорости и ускорения от времени показаны на рис.5.3.

Умножив обе части равенства уравнения (5.6) на массу m материальной точки получим

(5.7)

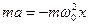
Используя II закон Ньютона, получаем

(5.8)

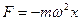
Рис.5.3.

Таким образом, чтобы совершались гармонические колебания на материальную точку должна действовать сила F, пропорциональная смещению x, которая возвращает ее в положение равновесия

(5.9)

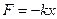
где, k – некоторый коэффициент (зависящий от свойств колеблющейся системы) и называемой жесткостью.

Из уравнения (5.7) и (5.8) видно, что .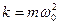

Кинетическая, потенциальная и полная энергии гармонических колебаний

Полная энергия Е колеблющейся материальной точки равна сумме кинетической Е_к и потенциальной Е_п энергий

Кинетическую энергию можно найти, зная массу m и скорость u

(5.11)

(5.12)

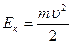
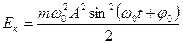
Выражение для потенциальной энергии можно найти из соотношений между потенциальной энергией и силой.

(5.13)

(5.14)

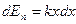
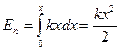
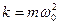
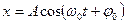
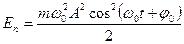
Учитывая, что и получаем

(5.15)

Полную энергию получим сложив (5.12) и (5.15)

(5.16)

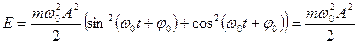
Таким образом, полная энергия пропорциональна квадрату амплитуды колебаний.

Из формул (5.12) и (5.15) видно, что когда 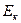увеличивается Е_п уменьшается и наоборот.

5.3. Уравнение гармонических колебаний.
Маятники

На колеблющуюся материальную точку массой m действует возвращающая сила F = — kx. Эта сила вызывает ускорение 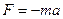. Равенство этих сил позволяет записать

где, k – жесткость системы, 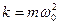; х – смещение; а – ускорение материальной точки.

Сделав соответствующие подстановки в (5.17), получим

или (5.18)

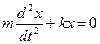
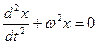
Уравнение (5.18) представляет собой дифференциальное уравнение второго порядка незатухающих гармонических колебаний материальной точки.

Решением этого дифференциального уравнения как раз и является уравнение (5.2): .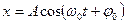

Колебания любого гармонического осциллятора (или гармонического вибратора) описываются дифференциальным уравнением второго порядка

(5.19)

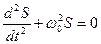
Решением этого уравнения является

(5.20)

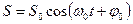
где S₀ – амплитудное (максимальное) значение параметра S.

Примерами гармонических осцилляторов являются маятники, колебательный контур.

В качестве примера малых колебаний рассмотрим колебания маятников.

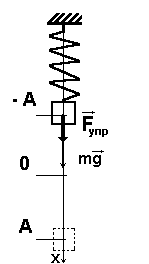
Пружинный маятник

Груз массой m, подвешенный на упругой пружине представляет собой пружинный маятник (рис.5.4). Если груз оттянуть вниз и отпустить, то под действием силы F = -kx маятник будет совершать колебания; k – коэффициент жесткости (в данном случае коэффициент упругости).

Рис.5.4.

Уравнение движения маятника имеет вид

или ,

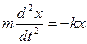
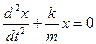
Его решением является

Это значит, что пружинный маятник совершает гармонические колебания с циклической частотой ω₀

, с другой стороны .

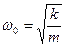
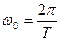
Период колебаний пружинного маятника

(5.21).

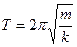
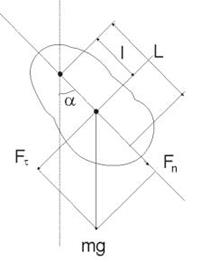
Физический маятник

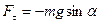
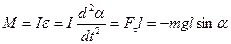
Физическим маятником называется твердое тело, которое может колебаться под действием силы тяжести вокруг оси, не проходящей через центр масс. При отклонении маятника относительно оси О угол α, на него действует М – момент возвращающей силы (рис.5.5)

(5.22)

где, I – момент инерции относительно оси О;

l – плечо силы F_τ; при малых углах .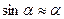

Рис.5.5.

Из (5.22) получаем дифференциальное уравнение

(5.23)

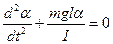
Сравнив уравнение (5.23) с уравнением гармонического осциллятора (5.19), получим

, (5.24)

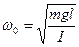
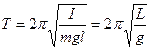
где, 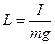– приведенная длина физического маятника.

От точки подвеса О на линии ОС на расстоянии L находится точка О₁, называемая центром качения. Точки О и О₁ обладает свойством взаимозаменяемости.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Энергия гармонических колебаний

Вы будете перенаправлены на Автор24

Колебания — это самая общая форма движения динамических систем около положения равновесия. При малых отклонениях от положения равновесия колебания обычно являются гармоническими. В этом заключается их особенная значимость.

где $omega^2$ — циклическая частота колебаний; $x$ -расстояние положения равновесия

называют уравнением механических гармонических колебания. Колебания происходят вдоль оси $X$.

Решением уравнения (1) можно считать функции:

$x=Asin (omega t+varphi)$ или

$x=Acos (omega t+varphi_1)$,

где $A$ — амплитуда колебаний.

Систему, которая реализует данные малые колебания, называют линейным или гармоническим осциллятором. Примером гармонического осциллятора может служить

1. малое тело, подвешенное на упругую пружину (Пружинный маятник);
2. физический маятник (Тело, которое совершает колебания относительно точки (или оси, проходящей через точку тела), не являющейся его центром масс);
3. математический маятник; (Малое тело, совершающее колебания на длинном, нерастяжимом, невесомом подвесе).

Собственными называют колебания системы под воздействием только внутренних сил при отсутствии внешних воздействий.

В полной механической энергии гармонического осциллятора выделяют:

• потенциальную энергию;
• и кинетическую энергию.

Видео:Урок 327. Гармонические колебанияСкачать

Потенциальная энергия

Говорить о потенциальной энергии можно только, если действующие силы потенциальны. Если колебательные движения между двумя точками являются одномерным, то автоматически обеспечивается условие потенциальности и всякую силу, зависящую только от координат, можно считать потенциальной.

Если рассматривается линейный осциллятор, то обычно считают, что потенциальная энергия точки равна нулю в положении равновесия. Считая, что осциллятор заставляет совершать колебания сила упругости;

и зная, как связана потенциальная энергия и потенциальная сила, (для одномерного случая: $F=-frac$), потенциальную энергию линейного осциллятора определим как:

Готовые работы на аналогичную тему

Из формулы (3) видно, что потенциальная энергия при колебаниях изменяется с течением времени, так как изменяется $x$. Частота колебаний потенциальной энергии $2omega$.

Видео:Превращение энергии при колебаниях. Уравнение колебательного движения. 1 часть. 9 класс.Скачать

Кинетическая энергия.

Кинетическая энергия тела – это энергия движения, она зависит от скорости перемещения материальной точки, задается выражением:

Кинетическая энергия является переменной во времени физической величиной. Колебания ее происходят с частотой $2omega$ (эта частота в два раза больше, чем частота колебаний $x$)

Видео:Превращение энергии при гармонических колебаниях Урок 117Скачать

Закон сохранения энергии при гармонических колебаниях

Как было отмечено, кинетическая энергия и потенциальная энергия являются переменными во времени величинами, однако, их сумма у гармонического осциллятора, выполняющего свободные колебания, не изменяется:

Полная энергия системы ($E$) не изменяется, поскольку при гармонических колебаниях выполняется закон сохранения механической энергии, так как сила упругости является консервативной.

Закон сохранения энергии позволяет сделать два существенных вывода

Вывод первый. Наибольшая кинетическая энергия осциллятора равна его наибольшей энергии потенциальной энергии.

Данный вывод очевиден, так как потенциальная энергия осциллятора максимальна при смещении точки выполняющей колебания на максимально возможное расстояние, при этом скорость, а соответственно и кинетическая энергия осциллятора равна нулю.

Наибольшую кинетическую энергию колебательная система имеет тогда, когда она проходит положение равновесия ($x=0$), то есть потенциальная энергия равна нулю.

где $V$ — максимальная скорость.

Вывод второй. Средняя кинетическая энергия осциллятора равна его средней потенциальной энергии.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Средняя кинетическая энергия.

Пусть параметр $f$ функция времени, тогда средняя ее величина на отрезке времени от $t_1$ до $t_2$ равна:

где пределы интегрирования обозначают 1 — время $t_1$; 2 — $t_2$.

Если функцию $f(t)$ изобразить на графике (рис.1), то ее среднее значение будет соответствовать высоте прямоугольника, площадь которого ограничивают функция $f$ и ось $t$ на заданном отрезке времени.

Площадь под осью $t$ считают отрицательной.

Рисунок 1. График. Автор24 — интернет-биржа студенческих работ

Запишем закон движения осциллятора как:

$x(t)=Acos (omega t+varphi) (7)$,

его скорость равна:

$dot=-Aomegasin (omega t+varphi) (8).$

Выражение для потенциальной энергии представим как:

Кинетическую энергию представит выражение:

Отрезком времени, на котором будем брать среднее, станет период колебаний, вернее одного колебания. Нахождение средних значений кинетической и потенциальной энергии сводят к поиску средних от $cos^2 (omega t+varphi)$ и $sin^2 (omega t+varphi)$:

$(sin^2 (omega t+varphi))_=fracint_0^T cos^2 (omega t+varphi)dt=fracint_0^Tfrac(1-cos 2(omega t+varphi)dt)=frac,$

где $T$ — период колебаний; $omega T=2pi.$

По аналогии получаем:

$sin^2 (omega t+varphi)_sr=frac.$

В результате имеем:

средняя по времени потенциальная энергия гармонического колебания за один период равна:

средняя по времени кинетическая энергия составила:

Сравнивая (10) и (11) мы видим, что:

где $E$ — полная механическая энергия гармонических колебаний.

то есть средняя по времени кинетическая энергия осциллятора равна средней по времени потенциальной энергии.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 05 2021

Видео:Физика 9 класс (Урок№11 - Гармонические колебания. Затухающие колебания. Резонанс.)Скачать

Энергия гармонических колебаний

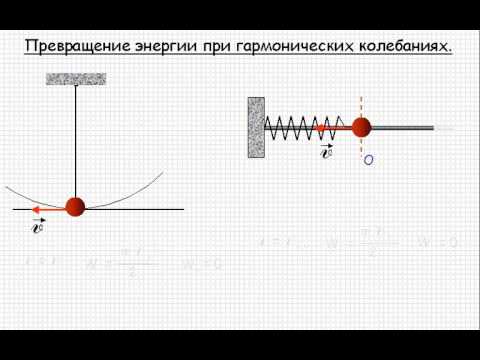
Рассмотрим превращения энергии, которые происходят при гармонических колебаниях в консервативной системе на примере пружинного маятника.

Видео:Гармонические колебания | Физика 11 класс #8 | ИнфоурокСкачать

Потенциальная энергия гармонических колебаний

В процессе механических колебаниях груза на пружине периодически кинетическая энергия ($E_k$) движущегося груза переходит в потенциальную энергию ($E_p$) колебательной системы, состоящей из потенциальной энергии упругодеформированной пружины и потенциальной энергии груза в поле тяжести Земли. Потенциальная энергия пружины при упругой деформации равна:

где $left(x+x_0right)$ — удлинение пружины; $k$ — жесткость пружины.

Потенциальную энергию груза в поле тяжести ($E_$) найдем как:

где $m$ — масса груза, прикрепленного к пружине.

Постоянную $C,$ будем выбирать так, чтобы в положении равновесия полная потенциальная энергия колебательной системы равнялась:

Тогда потенциальная энергия представлена выражением:

Видео:Физика ЦТ | Механические колебания. Часть 2. Преобразование энергии при гармонических колебанияхСкачать

Кинетическая энергия пружинного маятника

Кинетическая энергия рассматриваемой колебательной системы состоит из энергии движения груза. Используя уравнение смещения груза пружинного маятника при гармонических колебаниях, происходящих по оси X:

найдем уравнение изменения кинетической энергии груза. Для этого найдем скорость движения груза как:

В таком случае кинетическая энергия равна:

Видео:Гармонические колебанияСкачать

Полная механическая энергия консервативной колебательной системы

Так как пружинный маятник мы считаем консервативной системой, то механическая энергия ее постоянна:

Проверим справедливость выражения (8),) непосредственным суммированием правых частей выражений (4) и (7): (учитывая (5))

где $<_0>^2=frac$. Формула (9) показывает, что постоянная полная энергия колебательной системы равна потенциальной ее энергии в точках максимального отклонения от положения равновесия (при $x=pm A$). Энергия $E$ равна кинетической энергии при прохождении грузом положения равновесия, скорость груза равна:

В ходе взаимных превращений потенциальная и кинетическая энергии гармонически колеблются с одинаковой амплитудой, равной $frac$ в противофазе друг с другом, частота их колебаний равна $2_0$.

Видео:Физика 9 класс. §25 Гармонические колебанияСкачать

Примеры задач на энергию гармонических колебаний

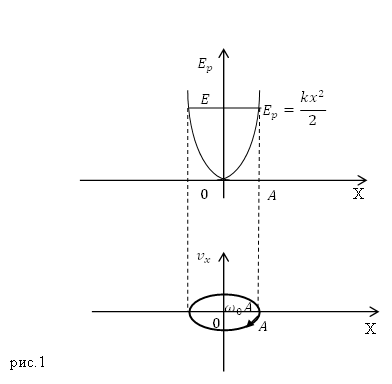
Задание. Что собой представляет фазовая траектория пружинного маятника, при рассмотрении его как гармонического осциллятора?

Решение. Уравнение фазовой траектории — это уравнение закона сохранения энергии:

Разделим обе части выражения (1.1) на $E$ получим:

Выражение (1.2) — это уравнение эллипса, полуоси которого равны $sqrt<2/>$ и $sqrt<2/>$.

Фазовую траекторию часто сопоставляют с графиком потенциальной энергии осциллятора. При этом в верхней части рисунка (рис.1) изображают график потенциальной энергии ($E_p(x)$), в нижней части изображают фазовую траекторию, которая соответствует колебаниям со значением полной энергии равной E, указанной на верхнем графике.

Задание. Материальная точка, имеющая массу $m=5cdot ^кг,$ совершает колебания в соответствии с законом: $xleft(tright)=<cos (fract)(м) >$. Какова полная энергия этой точки?

Решение. Полная энергия в консервативной колебательной системе величина постоянная и найти ее можно в соответствии с выражением:

Рассматривая уравнение колебаний точки, данное в условии задачи:

имеем: $A=1 м; _0=frac$. Вычислим искомую энергию:

📽️ Видео

Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

5.4 Уравнение гармонических колебанийСкачать

Урок 333. "Энергетический" метод расчета частоты свободных колебанийСкачать

Физика. 11 класс. Уравнение и графика гармонических колебаний /03.09.2020/Скачать

Урок 86 (осн). Энергия. Превращения энергииСкачать

Гармонические колебания.Отношение энергийСкачать

Кинетическая и потенциальная энергияСкачать

Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

гармонические колебанияСкачать