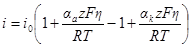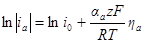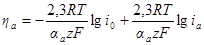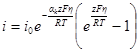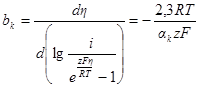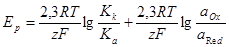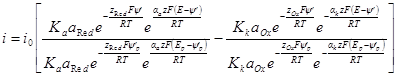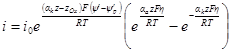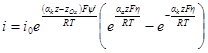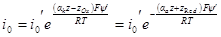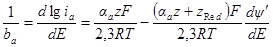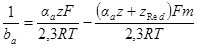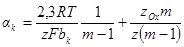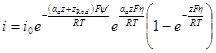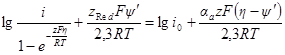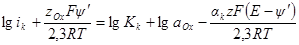Уравнение поляризационной кривой в случае перенапряжения диффузией

Видео:10.1 Закон Фика и уравнение диффузии моноэнергетических нейтронов (часть 1)Скачать

УРАВНЕНИЕ ПОЛЯРИЗАЦИОННОЙ КРИВОЙ

БЕЗ УЧЕТА СПЕЦИФИЧЕСКОЙ АДСОРБЦИИ И Ψ’-ПОТЕНЦИАЛА

Плотность тока, протекающего через электрод (регистрируемая прибором), всегда равна разности частных плотностей токов: i = i₂ – i₁. При равновесном потенциале измеряемый ток равен нулю и i₁ = i₂Значение частных плотностей токов при равновесном потенциале называется плотностью тока обмена i₀. Следовательно, если потенциал электрода равен равновесному (Е = Е_p), можно записать: i_l = i₂ = i₀ или, воспользовавшись последними уравнениями разд. 8.2:

При сдвиге потенциала от равновесного значения через электрод начинает протекать ток, равный разности

Умножим и разделим правую часть уравнения на i₀, причем в каждом из членов разности в знаменателе i₀ заменим на соответствующие члены предыдущего уравнения:

и

Из этого уравнения, называемого полным уравнением поляризационной кривой, следует, что при сдвиге потенциала от равновесного значения в катодную сторону (Е Е_р) i = i_a > 0. Таким образом, при указанной системе записи плотности тока i = i₂ – i₁ мы уславливаемся считать катодный ток отрицательным, а анодный положительным. Равноценна и противоположная система записи (i = i₁ – i₂), но мы ею не будем пользоваться.

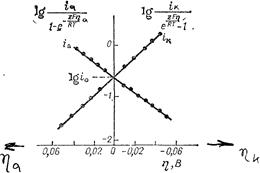
Соотношения между полной поляризационной кривой и частными поляризационными кривыми показаны на рис. 8.7.

При достаточно высоких катодных или анодных перенапряжениях измеряемый ток очень близок к i_к или i_а. Это связано с тем, что при увеличении перенапряжения один из экспоненциальных членов в последнем уравнении стремится к нулю. При потенциалах электрода, близких к равновесному, нельзя пренебречь ни одной из составляющих. В этом случае η x = 1 + х и е – x = 1 – х), получим:

Это уравнение называется полным уравнением поляризационной кривой при малых перенапряжениях. В координатах плотность тока — перенапряжение онопредставляет прямую линию с наклоном i₀(zF/RT), проходящую через начало координат, причем значение плотности тока не зависит от коэффициентов переноса. Область перенапряжений, в которой экспериментально реализуется линейная зависимость, невелика и, например, при отклонениях от линейности в

Рис. 8.7. Зависимость плотности тока от перенапряжения при α_к = α_а = 0,5.

1% составляет 0,013/z В, если α = 0,5. При уменьшении αобласть линейности резко сокращается и, когда α = 0,4, равна 0,0026/z В. Из наклона прямой di/dη = i₀(zF/RT) при малых поляризациях определяется ток обмена, а обратная величина dη/di, при η → 0 равная

получила название сопротивления переноса заряда постоянному току.

При высоких перенапряжениях, когда η >> (RT/zF) , один из членов разности в уравнении полной поляризационной кривой уменьшается, а другой — возрастает настолько, что уменьшившимся членом можно пренебречь. При катодном процессе, по условию, перенапряжение имеет отрицательный знак, при анодном — положительный. В соответствии с этим

;

;

Поскольку i_k отрицательно, в этих уравнениях под знаком логарифма стоит абсолютное ее значение.

В дальнейшем изложении мы не будем пользоваться обозначением |i_k|, но будем помнить, что i_k есть абсолютное значение катодной плотности тока. Кроме того, под знаком логарифма должна стоять плотность тока в безразмерных единицах, например в долях плотности тока обмена. Этим требованием обычно пренебрегают и выражают i_k в А/м 2 .

Оба уравнения могут быть представлены в форме

носящей название уравнения Тафеля.

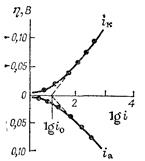
Построение катодной и анодной поляризационных кривых в полулогарифмических координатах позволяет определить значение плотности тока обмена, а также коэффициенты переноса (рис. 8.8). Экстраполяция линейных участков, подчиняющихся уравнению Тафеля, на нулевое перенапряжение дает значение логарифма плотности тока обмена.

По углам наклона линейных участков в координатах η — lg i определяют коэффициенты переноса:

;

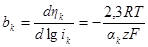
Рис. 8.8. Зависимость перенапряжения от плотности тока на амальгамном кадмиевом электроде в растворе CdSO₄ (концентрации 0,005 кмоль/м 3 ) + K₂SO₄ (концентрации 0,4 кмоль/м 3 ).

Рис. 8.9. Поляризационные кривые на амальгамном цинковом электроде в растворе перхлората цинка в диметилформамиде, построенные в координатах О. А. Есина.

Как показал О. А. Есин, уравнение полной поляризационной кривой может быть проанализировано и в общей форме. Вынося в этом уравнении один из членов разности за скобки и помня, что α_k + α_a = 1, получим:

или

;

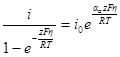
Два последних уравнения выражают соответственно истинные скорости анодного и катодного процессов и справедливы во всей области перенапряжений. Каждое из уравнений представляет прямую линию в координатах η — ( η — ) (рис. 8.9). Обе прямые проходят в области катодных и анодных перенапряжений и соответствуют истинной скорости анодного и катодного процессов как в катодной, так и в анодной областях перенапряжений. Прямые пересекаются при η = 0 и их точка пересечения на оси ординат дает значение логарифма плотности тока обмена. Коэффициенты переноса определяются из уравнений:

;

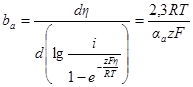
Используя выражения для частных поляризационных кривых, можно получить уравнение для равновесного потенциала. Так как i₁ = i₂ при Е = Е_p, получим:

Сравнивая последнее выражение с уравнением Нернста, получим:

Таким образом, стандартный потенциал электродной реакции зависит от соотношения констант скоростей катодного и анодного процессов.

Уравнения для частных поляризационных кривых при постоянных значениях а_Ox и a_Red в координатах Е — lg i являются прямыми линиями. По координатам точки пересечения прямых могут быть определены логарифмы плотности тока обмена и равновесный потенциал. Такой способ определения i₀ и Е_p часто применяется, так как не на всех электродах можно непосредственно измерить равновесный потенциал. Это связано с тем, что многие из электродов (Fe, Ni в растворах собственных ионов), а также некоторые окислительно-восстановительные электроды, имеют низкие токи обмена. В равновесных условиях на основную реакцию обмена накладываются побочные процессы, которые возникают в результате присутствия примесей на металле (окислы) или в растворе. Возможно также протекание неравновесных коррозионных процессов. Результатом является смещение измеряемого потенциала от равновесного потенциала основной реакции. Кроме того, при низких токах обмена равновесие устанавливается медленно.

Экстраполируя поляризационные кривые из области высоких катодных и анодных потенциалов, в отдельных случаях удается избежать влияния побочных процессов. С одной стороны, это связано с тем, что вклад в общий ток тока восстановления примеси незначителен ввиду малости ее концентрации, а с другой стороны — при этих потенциалах побочные реакции могут не протекать.

Как показывают экспериментальные данные, равновесные потенциалы, определенные из кинетических измерений, хорошо совпадают, когда это возможно, с полученными из измерения равновесий, и их совпадение является критерием обратимости электродной реакции (или истинного равновесия на электроде).

8.2.2. ВЛИЯНИЕ ψ’-ПОТЕНЦИАЛА НА СКОРОСТЬ РЕАКЦИИ РАЗРЯДА — ИОНИЗАЦИИ

ψ’-потенциал, с одной стороны, определяет активность частиц, находящихся непосредственно у поверхности электрода, (a_{Ox s}, a_{Red s})

;

а с другой — оказывает влияние на энергию активации, изменяя скачок потенциала в плотной части двойного слоя, который становится равным Е – ψ’.

В этих уравнениях a_Ox и a_Red — активности окисляющихся и восстанавливающихся частиц в объеме; z_Ox и z_Red — заряды этих частиц с учетом их знака.

Если ψ’-потенциал имеет одноименный знак с разряжающейся частицей, то активность ионов у поверхности электрода (в состоянии, предшествующем переносу заряда) будет меньше, чем в объеме, при разноименных знаках — больше, чем в объеме. На активность незаряженных частиц у поверхности ψ’-потенциал не влияет.

Уравнения для скоростей катодного и анодного процессов с учетом ψ’-потенциала, впервые полученные А. Н. Фрумкиным, запишутся в виде:

При равновесии ψ’ = ψ’_p и плотность тока обмена определяется уравнением:

После логарифмирования этого уравнения и решения его относительно Е_р получаем:

т. е. вновь приходим к формуле Нернста.

Из приведенного вывода следует важное заключение о том, что ψ’_p и, следовательно, строение двойного слоя не сказывается на величине равновесного потенциала.

Зависимость плотности тока от перенапряжения с учетом ψ’-потенциала будет иметь вид:

Величины α_az + z_Red и α_kz – z_Ox равны друг другу. В самом деле, решая равенство

при условии α_к + α_а = 1 приходим к очевидному выводу:

Поэтому уравнение поляризационной кривой с учетом ψ’-потен-циала может быть записано в виде:

Последние уравнения при учете ψ’-потенциала позволяют привести всю поляризационную кривую к потенциалу ψ’_p. Однако наиболее удобным является приведение кривой к потенциалу ψ’_p = 0. В этом случае уравнения имеют вид:

Для скоростей катодного и анодного процессов получим:

Сравнивая полученные уравнения с уравнениями без учета ψ’-потенциала, можно видеть, что

Здесь i₀’ — действительная плотность тока обмена в отличие от i₀, экспериментально получаемой экстраполяцией поляризационных кривых или другими методами.

Из кинетических уравнений для i_k и i_a имеем:

Следовательно, если в данных конкретных условиях ψ’-потенциал не зависит от потенциала электрода или зависит от него по закону ψ’ = const ± mE, то тафелевские зависимости остаются линейными, ибо dψ’/dE равно нулю либо постоянной величине m. Если же зависимость ψ’ от потенциала имеет более сложный вид, то тафелевские полулогарифмики становятся нелинейными.

При определении из наклона прямолинейных тафелевских зависимостей коэффициентов переноса α_k или α_a нужно помнить, что из выражений α_к = – 2,3RT/zFb_k и α_а = 2,3RT/zFb_a правильные значения получаются только в тех случаях, когда ψ’ = 0 или ψ’ ≠f(E). В случае же линейного изменения ψ’ с потенциалом

и расчет коэффициентов переноса по формулам, не учитывающим линейный ход ψ’ с потенциалом электрода, может привести при определенных значениях m к искажению величии α_к и α_а.

Для получения действительной плотности тока обмена и поляризационной кривой с поправкой на ψ’-потенциал применяют исправленные тафелевские зависимости (ИТЗ),

Из полного уравнения поляризационной кривой с учетом ψ’- потенциала получаем:

Преобразовываем эти уравнения:

Зная ψ’-потенциал, можно построить поляризационные кривые для истинных скоростей катодного и анодного процессов в координатах: левая часть последних уравнений — (η – ψ’). Полученные таким образом исправленные тафелевские зависимости справедливы во всей области потенциалов и дают действительные значения плотности тока обмена и коэффициентов переноса.

При достаточно высоких перенапряжениях ИТЗ, например, для катодного процесса можно получить в виде:

Исправленные тафелевские зависимости в соответствии с последним уравнением строят (рис. 8.10) в координатах [lg i_k + (z_OxFψ’/RT)]— (Е — ψ’); они справедливы в области достаточно высоких перенапряжений. Использование ИТЗ позволило, например, показать (А. Н. Фрумкин, Н. В. Николаева-Федорович), что влияние природы металла на скорость процесса восстановления анионов S₂O₈ 2– связано с изменением ψ’-потенциала.

Значение ψ’-потенциала рассчитывают на основании теории строения двойного электрического слоя. При этом предполагают, что потенциал на внешней плоскости плотной части двойного слоя (ψ’) равен потенциалу в плоскости, в которой находятся заряженные частицы (ψ₀).

Рис. 8.10. Исправленная тафелевская зависимость при восстановлении анионов S₂O₈ 2– в растворе NaF концентрации 9∙10 –3 кмоль/м 3 на электродах из Cd, Pb, Sn, Bi.

Видео:Электролиз. 10 класс.Скачать

Неравновесные электрохимические системы (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9

Пусть массоперенос электроактивного вещества к поверхности электрода происходит за счет диффузии. Если диффузия является лимитирующей стадией, то скорость электрохимического процесса в целом определяется скоростью диффузии, и величина плотности тока вычисляется при решении дифференциальных уравнений диффузионной кинетики.

Рассмотрим несколько диффузионных моделей: 1) стационарная; 2) линейная, полубесконечная к горизонтальному плоскому электроду (модель Коттрела); 3) линейная, к расширяющейся сфере (к поверхности РКЭ); 4) конвективная (вращающийся дисковый электрод). Модели описывают одномерную диффузию, в которой массоперенос осуществляется в направлении, перпендикулярном к поверхности электрода (ось x).

Для всех рассматриваемых моделей выполняется закон Фика:

. (10)

При различных граничных условиях этот закон имеет разные решения.

В этом разделе рассмотрим простейший случай стационарной диффузии, остальные диффузионные модели более подробно рассмотрим в разд. 2. Стационарная диффузия в эксперименте реализуется при интенсивном перемешивании раствора, содержащего фоновый электролит, электроактивное вещество, а также погруженный в этот раствор электрод.

Стационарная диффузия. Граничные условия:

при x = 0 (на поверхности электрода) концентрация равна С(0);

при x = δ (в объеме раствора) концентрация равна C *.

В стационарном состоянии реализуется условие , т. е. концентрация электроактивного вещества не зависит от времени и постоянна по всему объему раствора.

Уравнение Фика для стационарной диффузии выглядит так:

= 0.

Решение этого уравнения:

= const .

Видно, что градиент концентраций [ C * – C (0)] является постоянным, если на электроде не протекает реакция окисления/восстановления. Нернстом было введено понятие диффузионного слоя толщиной d , в котором концентрация электроактивного вещества изменяется от объемной (на границе диффузионного слоя при x = d ) до вблизи поверхности электрода (при x = 0). Отношение коэффициента диффузии к толщине диффузионного слоя Нернста (mi = ), называется коэффициентом массопереноса mi, его размерность см/с.

Если на электроде протекает реакция окисления/восстановления, то плотность тока электродной реакции равна:

,

.

Плотность тока достигает максимального (предельного) значения при Сi = Сi*:

, (11)

где mi – коэффициент массопереноса, см/с.

1.3.1. Уравнение обратимой поляризационной кривой

Выведем уравнение стационарной поляризационной кривой для зависимости тока ( I ) или плотности тока ( i ) от потенциала электрода (Е) для электродной реакции Ox z + ne g Red z – n , когда формы Ox и Red растворимы и концентрация Red в начальный момент времени равна 0. В зависимости от величины гетерогенной константы скорости переноса электрона k ° (точнее, соотношения ) уравнения поляризационных кривых будут различны.

Для вывода уравнения поляризационной кривой, необходимо знать зависимость потенциала электрода от концентрации электроактивных веществ. При изменении потенциала вблизи поверхности электрода концентрации Ox и Red меняются. При повышении потенциала электрода скорость электродной реакции увеличивается экспоненциально (уравнение Батлера – Фольмера (4)). При некотором значении Е скорость разряда-ионизации протекает мгновенно, и поверхностная концентрация электроактивного вещества Ox становится равной нулю (СOx(0) = 0). В этом случае процесс переходит в область диффузионной кинетики и плотность тока достигает максимального предельного значения:

. (11)

Если k ° велика (10–2 см/с), то вблизи электрода устанавливается равновесие форм Ox и Red и потенциал электрода описывается уравнением Нернста, только под ln записывается отношение концентраций электроактивных веществ на поверхности электрода С(0). Такие реакции в электрохимии носят название Нернстовых или обратимых. Запишем уравнение Нернста:

.

Считаем, что в процессе получения поляризационной (вольтамперной) кривой объемные концентрации веществ не меняются.

Измеряемый ток для процесса восстановления на катоде:

.

Измеряемый ток для процесса окисления на аноде:

.

Пусть в начальный момент времени Red в растворе отсутствует, С Red * =0. Выразим СОх(0) и СRed(0) через измеряемый ток i и предельный диффузионный ток id:

,

.

Подставим данные выражения для поверхностных концентраций в уравнение Нернста и получим уравнение обратимой поляризационной кривой:

. (12)

По определению , потенциал полуволны Е½ – это потенциал, при котором измеряемый ток достигает значения, равного половине (½) величины предельного диффузионного тока.

Для обратимой электродной реакции Ox z + ne– D Red z– n потенциал полуволны E½ равен:

E½.

1.3.2. Уравнение необратимой поляризационной кривой

Если k ° мала (10–4 – 10–6 см/с), то потенциал электрода не описывается уравнением Нернста, и для вывода уравнения поляризационной кривой следует воспользоваться уравнениями Батлера – Фольмера (1) и диффузионной кинетики (11). При решение этих уравнений приводит к выражению (13) для полностью
необратимой поляризационной кривой :

. (13)

Отношение называют критерием обратимости электрохимического процесса. Если £ 1, т. е. гетерогенная константа скорости электродной реакции превышает коэффициент массопереноса в 100 – 1000 раз ( kо > m О x ), то процесс описывается уравнением (12); поляризационная кривая («волна») является обратимой. В этом случае на поверхности электрода устанавливается равновесие (или квази-равновесие), описываемое уравнением Нернста. Если , т. е. «волна» является необратимой, и описывается уравнением (13).

В условиях стационарной диффузии mox = const и его значение составляет 10–2 – 10–3 см/с. З начения kо = 10–2 – 10–6 см/с.

В табл. 1 приведены значения m О x ( t ) в зависимости от диффузионных моделей для различных электрохимических методов, рассмотренных в разд. 2, а также расчетные значения kо , при которых электрохимические процессы будут описываться как обратимые. Из табл. 1 видно, что в квадратно-волновой полярографии, а также в методе вольтамперометрии при высокой скорости развертки потенциала все реальные процессы, для которых kо

10–2 –10–6 см/с , «выглядят» как необратимые.

Значения коэффициентов массопереноса и гетерогенных констант скорости, рассчитанные для различных электрохимических методов

при t =1–2 с

при t импульс = 10–3 – 10–6 с

Вольтамперометрия
с линейной разверткой
потенциала

1.3.1. Поляризационная кривая одноэлектронного окисления Y (С = 1 мМ) в присутствии 1 М KNO3 получена на графитовом электроде в условиях стационарной диффузии, коэффициент массопереноса 0,01 см/с. Начальный участок кривой дает в координатах Тафеля прямую с константами а = 1,15 В и в = 0,144 В. Определите природу перенапряжения при h = 0,5 В и концентрацию Y вблизи поверхности электрода.

Решение . Для того чтобы определить природу перенапряжения при h = 0,5 В, следует рассчитать и сравнить величины предельной плотности тока, а также тока, который наблюдался бы при заданном перенапряжении в отсутствии диффузионного торможения электродной реакции.

Для анодной реакции предельный диффузионный ток равен

.

При h = 0,5 В величина измеряемого тока i Т может быть рассчитана по уравнению Тафеля (7):

0,5 = 1,15 + 0,144 lg |iТ|,

|iТ| = 3,06 × 10–5 А/см2.

Поскольку |iТ| h = 0,5 В перенапряжение связано с замедленным разрядом-ионизацией.

Концентрацию Y вблизи поверхности электрода С Y (0) в данных условиях можно оценить по формуле

9,7 10–4 М.

Как видно, отличие приэлектродной концентрации (0,97 мМ) от объемной (1 мМ) весьма незначительно, чего и следовало ожидать в условиях замедленного разряда-ионизации. Однако в области смешанной кинетики и, особенно, в области концентрационной поляризации формула становится неверной.

В общем случае измеряемый ток может существенно отличаться от тока, рассчитанного по уравнению Тафеля (7). Выведем общее уравнение для расчета концентрации электроактивного вещества вблизи электрода С(0). Запишем уравнение (2) для скорости анодной электродной реакции с учетом массопереноса:

.

С другой стороны, для анодного процесса в условиях стационарной диффузии ток равен

.

Комбинируя приведенные выше уравнения и используя выражение (11) для предельного диффузионного тока, получим:

.

Рассчитаем С Y (0) по этому уравнению, получим величину 0,969 мМ. Легко убедиться, что это значение практически совпадает с рассчитанным выше (0,97 мМ).

1.3.2. Выведите выражение для обратимой поляризационной кривой для электродной реакции осаждения ионов металла М+ на электроде из этого же металла (Mz+ + z e D M) для случая стационарной диффузии. Считайте, что в процессе снятия кривой концентрация ионов металла не меняется. Чему будут равны анодный и катодный токи?

1.3.3. Выведите уравнение поляризационной кривой для обратимой электродной реакции X + 2e D 2Y. В начальный момент времени (t = 0) концентрация вещества Y в растворе равна нулю ( C Y * = 0). Диффузия стационарная.

1.3.4.* Для полуреакции А3+ + 2е D А+ формальный потенциал равен –0,500 В (относительно НВЭ), предельный катодный ток равен 4,00 мкА, предельный анодный ток равен –2,4 мкА. Концентрация А3+ и А+ равны 0,002 М и 0,001 М соответственно. Изменения концентраций в процессе снятия поляризационной кривой не происходит. Определите потенциал полуволны.

1.3.5.* Поляризационная кривая двухэлектронного восстановления Y (С* = 1 мМ) в присутствии 1 М KNO3 получена на твердом электроде в условиях стационарной диффузии, коэффициент массопереноса 0,01 см/с. Начальный участок кривой дает в координатах Тафеля прямую с константами а = –0,53 В и в = –0,072 В. Определите природу перенапряжения при h = –0,4 В и концентрацию Y вблизи поверхности электрода.

1.3.6.* Стационарная поляризационная кривая двухэлектронного восстановления А (С* = 2 ммоль/л, Е ° ´ = –0,25 В) спрямляется в координатах Е –. Тангенс угла наклона равен 31,2 В–1, а координата пересечения прямой с осью абсцисс равна –0,398 В. Установлено, что предельная катодная плотность тока равна 1,27 мА/см2. Определите, является данная стационарная поляризационная кривая обратимой или необратимой, и рассчитайте из приведенных экспериментальных данных максимально возможное число параметров.

1.3.7. Стационарная поляризационная кривая одноэлектронного восстановления А (С = 2 мМ, Е ° ´ = +0,50 В) спрямляется в координатах Е – . Тангенс угла наклона равен 38,9 В–1, а отрезок, отсекаемый на оси абсцисс равен +0,48 В. Установлено, что предельная катодная плотность тока равна 1,27 мА/см2. Определите, является поляризационная кривая обратимой или необратимой, и рассчитайте из приведенных экспериментальных данных максимально возможное число параметров.

Электродные процессы, сопряженные с гомогенными предшествующими или последующими химическими реакциями, весьма распространены. Рассмотрим несколько частных случаев.

Обозначения: r – обратимый « reversible », i – необратимый « irreversible », C – химическая реакция « chemical », Е – электродная реакция « electrode ».

CrEr -процесс – это обратимый электродный процесс (Er), сопряженный с предшествующей равновесной химической реакцией (Сr). Это наиболее простой случай, который реализуется, например, при электроосаждении металлов из растворов металлокомплексов, а также в полярографическом анализе.

Рассмотрим восстановление ионов металла Mn + на ртутном катоде с образованием амальгамы:

Считаем, что равновесие химической реакции комплексообразования не нарушается в результате протекания электродной реакции. Тогда для любых значений x , характеризующих расстояние от поверхности электрода, константа устойчивости комплекса ML p выражается:

.

Если константа устойчивости комплекса велика ( b >> 106) и концентрация лиганда значительно превышает концентрацию ионов металла (С L >> CM n + ), то ионы металла в растворе присутствуют практически только в виде комплекса ML p .

Если электродная реакция обратимая, то потенциал электрода описывается уравнением Нернста:

.

Подставляя [ M n + ] в это уравнение, получим:

Для случая, когда С M в амальгаме в начальный момент времени равна нулю и диффузия стационарная получим уравнение для обратимой поляризационной кривой («волны»):

где ,

mK и mM – коэффициенты массопереноса комплекса ML p в растворе и атомов металла в амальгаме соответственно. Обратите внимание, что id определяется объемной концентрацией ML p , а не M n + .

Из полученных уравнений видно, что поляризационная кривая при наличии сопряженной равновесной химической реакции имеет форму обратимой «волны», смещенной в область отрицательных потенциалов, причем величина смещения ( D ) определяется константой равновесия, или константой устойчивости комплекса b :

D = .

Измеряя величины D при различных концентрациях лиганда, можно определить как константу устойчивости комплекса b , так и его состав (количество лигандов р).

CiEr -процесс – это обратимый электродный процесс (Er), сопряженный с предшествующей химической реакцией (Сi).

Рассмотрим химическую реакцию первого порядка, константа скорости ( k 1 ) которой недостаточно велика для установления равновесия в приэлектродном слое. Эта реакция предшествует обратимой электродной реакции.

Запишем схему этого электрохимического процесса:

A Ox ,

Для того чтобы дать представление о влиянии предшествующих химических реакций на кинетику электродных процессов, приведем упрощенное решение, предложенное Визнером и Брдичкой в рамках концепции реакционного слоя для полярографии на РКЭ.

Рассмотрим два случая: 1) k 1 >> k –1 , и константа равновесия химической реакции K велика, >> 1; 2) k 1 k –1 , и константа равновесия химической реакции K мала, . Очевидно, что в случае (1) при K >>1 химическая реакция не будет влиять на кинетику электродной реакции. Для случая (2) при достаточно больших катодных перенапряжениях ток достигает предельной величины i lim , которая определяется как диффузионными, так и кинетическими параметрами процесса:

Видео:Лекция 127 Поляризационная кривая в условиях перемешивания электролитаСкачать

Кинетика электродных процессов алюминия

Видео:Лекция 164 Влияние ДЭС на стадию разряда Электровосстановление анионовСкачать

КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ АЛЮМИНИЯ

В условиях электролиза при прохождении тока через электрод изменяется величина электродного потенциала по сравнению с его равновесным значением. Это изменение электродного потенциала называется поляризацией электрода или перенапряжением электродной реакции. Поляризация вызвана протеканием электрохимического процесса, и поэтому всегда имеется связь между скоростью процессса, а значит, плотностью тока на электроде, и поляризацией . Задача электрохимической кинетики состоит в установлении характера этой связи, чтобы сознательно управлять течением электрохимического процесса.

Электрохимический процесс складывается из нескольких последовательных стадий: транспорта вещества к поверхности электрода, электрохимической реакции восстановления или окисления на электроде и отвода продуктов реакции. В некоторых случаях существенную роль играют химические реакции: гомогенная, протекающая в электролите вблизи поверхности электрода, и гетерогенная — на поверхности электрода. В первом случае в электрохимическую реакцию вступает не то вещество, которое транспортируется к электроду, а продукты его распада или взаимодействия с другими веществами, содержащимися в электролите. Такая реакция предшествует электрохимической стадии. Во втором случае в результате электрохимического разряда получается не конечное вещество, а некоторое промежуточное, адсорбированное электродом. Затем происходит гетерогенная реакция перехода этого вещества в конечный продукт. Иногда приходится учитывать скорости образования новой фазы, появляющейся в результате электрохимической реакции — кристаллов твердого вещества, капель металла и пузырьков газа.

В зависимости от того, какая из этих стадий является лимитирующей, т. е. самой медленной, различают следующие виды поляризации, или перенапряжения (по Феттеру).

Перенапряжение перехода вызвано замедленностью стадии разряда — ионизации. Связь между перенапряжением и плотностью тока описывается уравнением Тафеля:

где С — плотность тока, А/см 2 ; а и b — постоянные. Для анодного процесса

где k₁, —константа скорости электрохимического процесса, 1/с; α — коэффициент переноса (кинетический коэффициент), доли. ед.

При электрохимическом процессе потенциальная энергия иона в электролите и конечного продукта на электроде различна. В энергию активации электродной реакции входит не вся разность этих энергий, а только часть ее. Коэффициент переноса й представляет собой отношение этой части энергии к полной энергии.

Для катодного процесса, в котором играет роль концентрация (активность) потенциал-определяющих ионов, константы уравнения Тафеля будут иметь значения:

где С — концентрация ионов, моль/см 3 ; β — коэффициент переноса для катодного процесса, доли ед.

Сумма коэффициентов переноса а и В равна единице и обычно принимается, что α = β =0,5.

Любой электрохимический (и химический) процесс идет как в прямом, так и в обратном направлениях. Чем дальше процесс от равновесного, тем больше прямой процесс преобладает над обратным, и наоборот. При равновесии скорости прямого и обратного процессов равны. Ток обмена и представляет собой скорость электрохимического процесса в прямом и обратном направлениях при равновесном потенциале. Как следует из соотношения , с увеличением тока обмена перенапряжение перехода уменьшается. Если i₀»i, то перенапряжение близко к нулю, и процесс можно рассматривать как равновесный (обратимый).

Обычно токи обмена в расплавленных солях велики—от единиц до сотен ампер на квадратный сантиметр, что связано с ускорением процессов при высоких температурах.

Перенапряжение диффузии

Возникает вследствие замедленности переноса реагирующих веществ. Этот перенос может осуществляться молекулярной диффузией, миграцией (переносом под действием электрического поля заряженных частиц — катионов и анионов) и конвекцией (переносом потоком жидкости). Обычно конвекция вызвана выделяющимися на аноде газами. Эффект миграционного переноса удается в значительной степени снизить за счет создания фона, при котором перенос электричества осуществляется другими, неразряжающимися ионами. Именно такой перенос имеет место в алюминиевых электролизерах.

Основным лимитирующим процессом обычно является молекулярная диффузия как самый медленный процесс. Если диффузия происходит к плоскому электроду, то диффузионный, ток (для катодного процесса) можно подсчитать из выражения первого закона Фика:

, где С₀ — концентрация ионов в глубине электролита; C₈—концентрация ионов на поверхности электрода;-δ — толщина диффузионного слоя; D — коэффициент диффузии.

Толщина диффузионного слоя зависит от условий перемешивания электролита — чем выше скорость потоков, обтекающих электрод, тем меньше б. При электролизе расплавленных солей толщина, диффузионного слоя обычно составляет от 0,1 до 1 мм.

Для жидких электродов в расплавленных солях было отмечено (Поляков с сотр.), что толщина диффузионного слоя уменьшается за счет эффекта Марангони: межфазное натяжение на границе металл — электролит имеет разное значение на различных участках поверхности электрода, что вызывает течение жидкости от участков с меньшим межфазным натяжением к участкам с большим межфазным натяжением. Это дополнительное перемешивание может уменьшить δ на порядок.

При падении концентрации С, до нуля получается максимальный ток диффузии — так называемый предельный диффузионный ток: i_d=nFDC_0/δ.

Связь между перенапряжением и диффузионным током дается выражением:

из которого следует, что в области предельного тока происходит резкий сдвиг потенциала в отрицательную сторону и на поляризационной кривой отмечается площадка предельного тока. Потенциал электрода при этом сдвигается настолько, что начинается разряд другого, более электроотрицательного катиона (например, катиона фона). Если строить поляризационную кривую до предельного тока, то в координатах η_d-1n (1 -i/i_d) получается прямая, наклон которой позволяет определить п — число электронов, участвующих в электрохимической реакции.

Если перенапряжение определяется замедленностью диффузии анионов в процессе анодного разряда, то соответствующее уравнение связи между током диффузии и перенапряжением будет

где i_d — предельный ток диффузии анионов, А/см 2 .

Перенапряжение реакции

Вызвано замедлением химических реакций на стадиях до или после разряда — ионизации. Рассмотрим гетерогенную реакцию, следующую после разряда, как наиболее важную для дальнейшего изложения.

Предположим, что электрохимический процесс состоит из двух последовательных стадий: окисления вещества R: R — ne ⇄ Oс образованием промежуточного окисленного вещества О, адсорбирующегося на поверхности электрода, и гетерогенной реакции O ⇄ A , при которой образуется конечный продукт А. Допустим, что стадия разряда протекает быстро, практически равновесно, в то время как последующая гетерогенная реакция — медленно. Скорость этой медленной стадии слагается из скорости прямого процесса, пропорциональной поверхностной концентрации вещества О в степени р (порядок реакции), и скорости обратного процесса υ = υ — υ = kC₀ p —υ , где k — константа скорости реакции, см/с.

При равновесии скорости этих процессов равны: υ₀=υ=υ =kC₀ p при этом С₀ — поверхностная концентрация вещества в равновесии, моль/см 2 . Если в процессе имеется большой избыток вещества А и его концентрация не зависит от потенциала, то независимой будет и C₀ Перенапряжение реакции определяется выражением:

где С₀—поверхностная концентрация вещества О при поляризации. Скорость процесса, или плотность тока

Ho nFυ₀= i₀ — плотность тока при равновесии (ток обмена), поэтому

Из выражений (34) и (35) вытекает связь между плотностью тока и перенапряжением:

Если i/io » 1, то получится уравнение Тафеля:

В координатах η_р — ln i эта зависимость выражается прямой линией, как и в случае перенапряжения перехода, но вместо коэффициента переноса здесь фигурирует порядок гетерогенной химической реакции р, и коэффициент b в уравнении Тафеля будет существенно меньшим.

Механизм катодного процесса алюминия

Катодный процесс включает в себя следующие последовательно идущие стадии: транспорт оксифторидных и фторидных комплексов, содержащих ионы алюминия, из глубины расплава к катоду; распад комплексов в двойном слое с образованием свободных ионов Аl 3+ . и разряд ионов Аl 3+ . Не исключено, что разряд происходит непосредственно из комплексных ионов, минуя стадию их распада. При восстановлении алюминия из криолито-глиноземных расплавов на индифферентном катоде (например, вольфрамовом) обнаруживаются на поляризационных кривых две площадки (Антипин), отвечающие двум процессам: Аl 3 +2е = Аl+, Аl + +е = Аl. Если катод — жидкий алюминий, процесса перезаряда нет, поскольку в присутствии алюминия быстро устанавливается равновесие между ионами Al 3+ , Аl + и металлом.

Импедансные измерения, т. е. исследование комплексного сопротивления электродной системы алюминий — криолито-глиноземный расплав в цепи переменного тока

в зависимости от частоты, позволили оценить величину тока обмена для этой системы. Оказалось, что ток обмена при температуре электролиза составляет около 20 А/ /см 2 , т. е. алюминиевый электрод является практически обратимым и перенапряжение перехода составляет всего несколько милливольт. Эти измерения указали на диффузионный характер перенапряжения.

Исследования поляризации алюминиевого электрода в лабораторной ячейке (Борисоглебский и др.) в условиях, когда анодный процесс сводился к растворению алюминия (т. е. анодных газов не выделялось) и перемешивание анолита и католита было минимальным, показало, что на поляризационных кривых имеются площадки предельного тока (рис. 17, кривая /).

С повышением температуры и при перемешивании расплава предельная плотность тока повышается. Катодный выход по току при достижении предельной плотности тока проходит через максимум (кривая 2) и содержание натрия в алюминии (кривая 3) скачкообразно повышается до предельной растворимости при данной температуре. Все эти факты несомненно указывают на диффузионный характер перенапряжения на алюминиевом катоде.

Рис. 17. Совместное выделение алюминия и натрия в условиях лабораторного эксперимента при 970 °С, К.О. = 3,0, концентрация Аl2O3 —5% (по массе) (Борисоглебский): 1—катодная поляризационная кривая; 2 — выход по току для алюминия; 3 — содержание натрия в алюминии

С ростом плотности тока в прикатодном слое уменьшается концентрация комплексных оксифторидных и фторидных ионов, содержащих катионы Аl 3+ , и увеличивается концентрация ионов Na + . Поскольку электрод обратимый (перенапряжение перехода отсутствует), рост концентрации ионов Na+ приводит к повышению содержания натрия в алюминии и сдвигу потенциала в отрицательную сторону. Следовательно, происходит совместный разряд ионов алюминия и натрия, только натрий не выделяется в виде отдельной фазы (пузырька при атмосферном давлении), а растворяется в алюминии и в солевом расплаве.

При предельной плотности тока потенциал достигает величины, при которой происходит выделение натрия в виде самостоятельной фазы, содержание натрия становится предельным при данной температуре. Дальнейшее повышение плотности тока приводит к уменьшению выхода по току для алюминия, поскольку все большие количества натрия разряжаются при неизменном количестве образующегося алюминия. Содержание натрия в алюминии не изменяется, так как достигнут предел его растворимости.

Таким образом, при -всех условиях электролиза имеет место совместный разряд алюминия и натрия, причем последний обычно выделяется в виде раствора в алюминии. Поскольку оба металла выделяются на одном электроде, их потенциалы должны быть одинаковы:

При поляризации католит обогащается фторидом натрия и обедняется фторидом алюминия по сравнению с равновесным составом. Поэтому величина поляризации катода равна э. д. с. концентрационной цепи:

Здесь в первом полуэлементе представлены состав электролита и сплава алюминий — натрий для равновесного электрода, во втором — для поляризованного,

Э. д. с. цепи равна

Диффузионный потенциал на границе раздела полуэлементов:

поскольку ток переносится только ионами натрия. Поэтому

Используя выражение для константы равновесия реакции

Катодное перенапряжение может быть определено, если известно содержание натрия в алюминии для равновесного электрода и для поляризованного. Поскольку концентрация натрия в растворе с алюминием мала, отношение активностей можно заменить отношением концентрации:

Многочисленные измерения концентрации натрия в алюминии на промышленных электролизерах показывают, что содержание натрия обычно меньше или равно его равновесному значению.

Электролит и металл в промышленных ваннах находятся в непрерывном движении, при этом на поверхности металла образуются волны. Движение электролита и металла способствует снятию перенапряжения диффузии, и алюминиевый электрод является практически равновесным.

Выделение натрия на алюминии определяется в основном криолитовым отношением и температурой: чем они выше, тем больше выделяется натрия. Натрий уходит из алюминия двумя путями: 1) растворяется в электролите, переносится к аноду и окисляется; 2) проходит через толщу алюминия и поглощается угольной футеровкой. Первый путь приводит к значительным потерям тока и к снижению выхода по току, второй — к преждевременному разрушению угольной футеровки электролизеров.

Статья на тему Кинетика электродных процессов алюминия

Похожие страницы:

Понравилась статья поделись ей

Leave a Comment

Для отправки комментария вам необходимо авторизоваться.

💥 Видео

Уравнение НернстаСкачать

Лекция 122 Второе уравнение диффузионной кинетикиСкачать

Лекция 177 Многостадийные реакции с последовательным переносом электроновСкачать

Лекция 173 Рекомбинационная теория ТафеляСкачать

Лекция 6Скачать

Лекция 152 Изучение стадии разряда ионизацииСкачать

Билет №04 "Потенциал электростатического поля"Скачать

Электрохимия1Скачать

Поляризация электродовСкачать

Лекция №3 "Электростатика. Поляризация диэлектриков"Скачать

Теории кислот, оснований и растворов. Теория Аррениуса-Оствальда. 11 класс.Скачать

Механизм электролитической диссоциации. 9 класс.Скачать

Классификация четырехполюсников. Системы уравнений четырехполюсниковСкачать

ЭП в веществе 2 Виды поляризацииСкачать

Лекция 4Скачать