В задачах с параметрами Профильного ЕГЭ по математике вам встретятся не только графики функций (в школьном смысле этого слова), но и множества точек на плоскости.
Вот несколько уравнений и неравенств, задающих окружность, круг, ромбик, отрезок. Заметим, что окружность или ромбик, хотя и задаются уравнениями, не являются графиками функций в школьном смысле этого слова. Чтобы лучше почувствовать эту разницу, повторите тему «Что такое функция».
Задачи с параметрами на ЕГЭ по математике считаются одними из самых сложных. Однако на самом деле они похожи на конструктор, где вы собираете решение из готовых элементов. Чтобы уверенно решать задачи с параметрами, необходимо отлично знать 5 типов элементарных функций и их графики. Преобразования графиков функций. И вот эти базовые элементы:
1. Уравнение задает окружность с центром в начале координат и радиусом
2. Уравнение задает окружность с центром в точке (a;b) и радиусом
3. Неравенство задает круг вместе с границей.
4. Уравнение задает верхнюю полуокружность с центром в начале координат и радиусом
5. Уравнение задает нижнюю полуокружность с центром в начале координат и радиусом
6. Уравнение задает верхнюю полуокружность центром в точке и радиусом
7. Уравнение при положительных и задает ромбик, симметричный относительно начала координат.
8. Уравнение (сумма модулей) задает график следующего вида:
9. Расстояние между точками и находится по формуле:
Координаты середины М отрезка АВ находятся по формуле:
Уравнение отрезка концы отрезка и
В левой части уравнения сумма расстояний от точки P с координатами до точек и В правой расстояние между точками и
Пара чисел соответствует координатам любой точки этого отрезка.
Кратко это можно записать так: Это значит, что точка P лежит на отрезке
- Окружность в полярных координатах
- Построение окружности по простому уравнению в полярной системе координат
- Еще одно уравнение окружности в полярных координатах
- Уравнение окружности в полярных координатах
- Построение окружности в полярной системе координат
- Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах
- Уравнение полуокружности со смещенным центром
- 📺 Видео
Видео:Уравнение окружностиСкачать

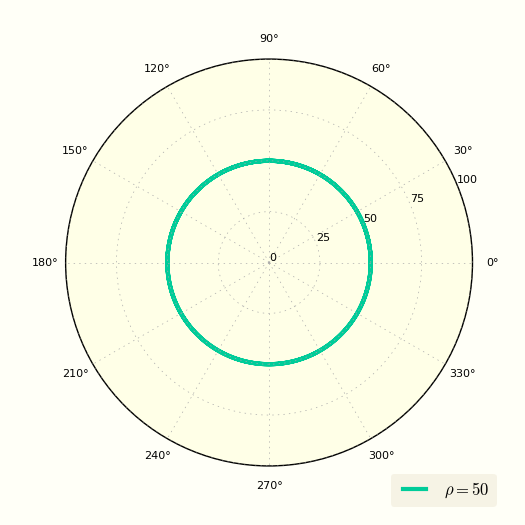
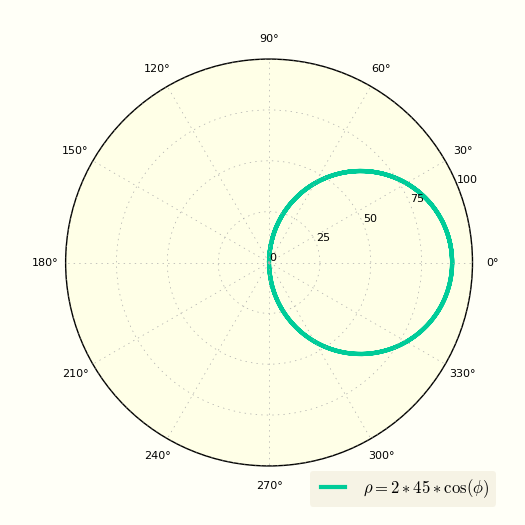
Окружность в полярных координатах
Уравнение окружности в полярных координатах выглядит очень просто
Это уравнение показывает, что ρ вообще не зависит от угла φ.
Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Построение окружности по простому уравнению в полярной системе координат
Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Еще одно уравнение окружности в полярных координатах
Первый пример был очень простым, теперь возьмем окружность смещенную по оси X в декартовых координатах и получим ее полярное уравнение.
Известно, что окружность в декартовой прямоугольной системе координат описывается уравнением:
Используя эти формулы и подставив их в (1) мы получим:
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Уравнение окружности в полярных координатах
Изначально после подстановки имеем
И этого уравнения получается система
Первое уравнение системы описывает полюс окружности.
Второе описывает саму окружность в полярной системе координат.
В итоге получаем:
Видео:11 класс, 20 урок, Уравнение сферыСкачать

Построение окружности в полярной системе координат
Видео:Уравнение окружности (1)Скачать

Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах
В данном варианте мы сместим окружность по оси Y в декартовых координатах и получим ее полярное уравнение.
При таком смещении окружность описывается уравнением:
И этого уравнения получается система
Первое уравнение системы описывает полюс окружности.
Второе описывает саму окружность в полярной системе координат.
Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Уравнение полуокружности со смещенным центром
Справочный материал по Планиметрии.
1. Основные аксиомы и теоремы.
Аксиома 1.1. Какова бы ни была прямая, существую точки, принадлежащие этой прмой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.
Аксиома 1.2. Из трех точек на прямой одна и только одна лежит между двумя другими.
Аксиома 1.3. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Аксиома 1.4. Прямая разбивает плоскость на две полуплоскости.
Аксиома 1.5. Каждый угол имеет определенную грудусную меру, большую нуля. Градусная мера угла равна сумме градусных мер углов, на которую он разбивается любым лучом, проходящим между его сторонами.
Аксиома 1.6. На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.
Аксиома 1.7. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 градусов, и только один.
Аксиома 1.8. Через точку, не лежащую на данной прямой, можно провести плоскоть не более одной прямой, параллельной данной.
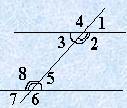
Теорема 1.1. Сумма смежных углов равна 180 градусам.
Теорема 1.2. Вертикальные угла равны.
Теорема 1.3. Две прямые, параллельные третьей, параллельны.
Теорема 1.4. Признаки параллельности прямых
Две прямые параллельны, если:
· внутренние накрест лежащие углы равны: 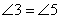
· внешние накрест лежащие углы равны: 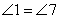
· соответственные углы равны: 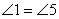
· сумма внутренних односторонних углов равна 180 градусам:
· сумма внешних односторонних углов равна 180 градусам:
Теорема 1.5. Геометрическое место точек, равноудаленных от двух данных точек, есть прямая, перпендикулярная к отрезку, соединяющему эти точки, и проходящая его середину.
Теорема 1.5. Теорема Фалеса. Параллельные прямые, пересекающие стороны угла, отсекают от них пропорциональные отрезки.
2. Произвольные треугольники.
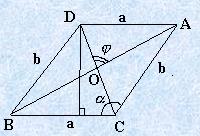
Пусть a , b , c –стороны треугольника; 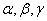
Теорема 2.1. Сумма углов треугольника равна 180 градусам.
Теорема 2.2. Условие существование треугольника. Для существования треугольника со сторонами a , b , c необходимо и достаточно выполнения трех неравентсв
Теорема 2.3. Монотонная зависимость сторон треугольника от углов. Если 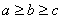
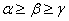
Определение 2.1. Высотой треугольника называется отрезок перпендикуляра, опущенного из вершины треугольника на противоположную сторону или её продолжение.
Примечание: Три высоты треугольника пересекаются в одной точке, называемой ортоцентром.
Определение 2.2. Биссектрисой внутреннего угла треугольника называют отрезок прямой, делящий данный угол на две равные части.
Примечание: Три биссектрисы пересекаются в одной точке, являющейся центром вписанной в треугольник окружности.
Теорема 2.4. Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.
Определение 2.3. Медианой треугольника называется отрезок прямой, проведенный из вершины треугольника, лежащий внутри треугольника и делящий противоположную сторону пополам.
Теорема 2.5. Три медианы треугольника пересекаются в одной точке, и точкой пересечения делятся в отношении 2:1, считая от соответствующих вершин.
Теорема 2.6. Средняя линия треугольника (отрезок, соединяющий середины сторон треугольника) параллельна его третьей стороне и равна её половине.
1.
2.
4.
5.
6. Теорема косинусов
7. Теорема синусов
8. 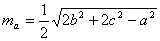
9. 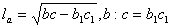
10. 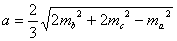
11. (очень полезная формула)
Теорема 2.7. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Признаки равенства треугольников.
Два треугольника равны, если:
· две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника;
· сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника;
· три стороны одного треугольника соответственно равны трем сторонам другого треугольника.
Признаки подобия треугольников.
Два треугольника подобны, если:
· два угла одного треугольника соответственно равны двум углам другого треугольника;
· две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны;
· стороны одного треугольника пропорциональны сторонам другого.
С- длина окружности; R – радиус; S – площадь круга; l – длина дуги; 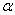
Определение 3.1. Окружностью называется фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Определение 3.2. Угол, образованный двумя радиусами окружности называется центральным углом.
Определение 3.3. Круговым сектором называется часть круга, лежащая внутри соответствующего центрального угла.
Определение 3.4. Круговым сегментом называется общая часть круга и полуплоскости.
1. 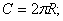
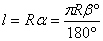
4. Площадь сектора AOBl :
5. Площадь сегмента AlB :
Теорема 3.1. Измерение углов, связанных с окружностью .
· величина центрального угла равна величине дуги, на которую он опирается;
· величина вписанного угла равна половине угловой величины дуги, на которую он опирается;
· вписанный угол, опирающийся на диаметр равен 90 градусов;
· величина угла, образованного касательной и хордой, имеющими общую точку на окружности, равна половине угловой величины дуги, заключенной между его сторонами;
· величина угла с вершиной внутри круга равна полусумме угловых величин дуг, заключенный между его сторонами и их продолжениями;
· величина угла с вершиной вне круга равна полуразности угловых величин большей и меньшей дуг, заключенных между ними.
Теорема 3.2. Свойства хорд, секущих и касательных.
· радиус, проведенный в точку касания касательной перпендикулярен ей;
· отрезки касательных, проведенных из общей точки к окружности равны;
· дуги, заключенные между параллельными хордами, равны
· диаметр, перпендикулярный к хорде, делит ее пополам.
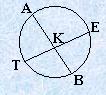
Теорема 3.3. Квадрат касательной, проведенной из данной точки к окружности равен произведению секущей, проведенной из этой же точки на ее внешнюю часть, т.е. 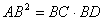
Теорема 3.4. Произведение отрезков хорд, проходящих через данную точку внутри круга, есть величина постоянная, т.е.
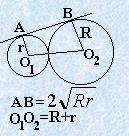
Теорема 3.5. Линии центров 2-х касающихся окружностей проходит через точку касания. Необходимое и достаточное условие касание извне двух окружностей радиусов R и r : длина отрезка общей касательной, заключенной между точками касания с окружностями, равна
Теорема 3.6. Для того чтобы в выпуклый четырехугольник можно было вписать окружность, необходимо и достаточно, чтобы суммы длин противолежащих сторон были равны друг другу.
Теорема 3.7. Для того чтобы около выпуклого четырехугольника можно было описать окружность, необходимо и достаточно, чтобы суммы противолежащих углов были равны 180 градусам.
4. Прямоугольный треугольник.
Пусть a , b – катеты; с – гипотенуза; 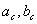
Определение 4.1. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Определение 4.2. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Определение 4.3. Тангенсом острого угла называется отношение противолежащего катета к прилежащему 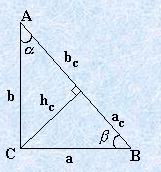
1. 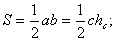
4. 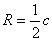
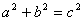
Теорема 4.1. В прямоугольном треугольнике квадрат высоты, проведенной к гипотенузе, равен произведению проекций катетов на гипотенузу:
Теорема 4.2. В прямоугольном треугольнике квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу: 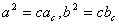
Признаки равенства прямоугольных треугольников.
Два прямоугольных треугольника равны, если:
· катеты одного треугольника соответственно равны катетам другого треугольника;
· гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника;
· катет и острый угол одного треугольника соответственно равны катету и острому углу другого треугольника;
· гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника.
5. Выпуклые четырехугольники.
Определение 5.1. Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Определение 5.2. Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Четырехугольник является параллелограммом, если
· его диагонали пересекаются и точкой пересечения делятся пополам;
· его противоположные стороны попарно равны;
· две противолежащие стороны равны и параллельны.
- диагонали параллелограмма пересекаются и точкой пересечения делятся пополам;
- противолежащие углы и стороны равны
- сумма внутренних углов параллелограмма, прилежащих к одной стороне, равна 180 градусам;
- сумма квадратов диагоналей равна сумме квадратов сторон.
Пусть a , b – смежные стороны 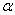
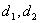
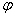
1.
2.
Определение 5.3.Прямоугольник – это параллелограмм, у которого все углы прямые.
- прямоугольник обладает всеми свойствами параллелограмма;
- у прямоугольника диагонали равны;
- около прямоугольника можно описать окружность с центром в точке пересечения диагоналей и радиусом, равным половине диагонали.
Определение 5.4. Ромб – это параллелограмм, у которого все стороны равны.
- ромб обладает всеми свойствами параллелограмма;
- диагонали ромба взаимно перпендикулярны и являются биссектрисами углов;
- в ромб можно вписать окружность с центром в точке пересечения диагоналей и радиусом, равной половине высоты ромба.
Определение 5.5. Квадрат – это прямоугольник, у которого все стороны раны. Квадрат – это ромб, у которого все углы прямые.
· квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба;
· около квадрата можно описать окружность с центром в точке пересечения диагоналей и радиусом, равным половине диагонали;
· в квадрат можно вписать окружность с центром в точке пересечения диагоналей и радиусом, равным половине стороны.
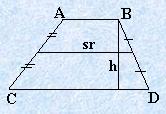
Определение 5.6. Трапеция – это выпуклый четырехугольник, у которого две противолежащие стороны (основания) параллельны, а две другие непараллельны.
Пусть a , b – основания трапеции; h – высота; sr – средняя линия; S – площадь трапеции.
1. 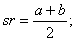
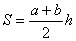
Теорема 5.1. Квадрат высоты равнобедренной трапеции, в которую можно вписать окружность, равен произведению оснований трапеции.
Теорема 5.2. Площадь равнобедренной трапеции, у которой диагонали взаимно перпендикулярны, равна квадрату её высоты.
Определение 6.1. Простая замкнутая ломаная называется многоугольником, если ее соседние звенья не лежат на одной прямой.
Теорема 6.1. Сумма углов выпуклого n -угольника равна
Определение 6.2. Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.
Теорема 6.2. Правильный выпуклый многоугольник является вписанным в окружность и описанным около окружности.
Пусть 
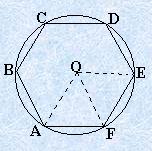
1. 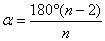
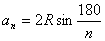
Таблица значений радиусов вписанной и описанной окружностей в часто встречающихся правильных многоугольников, выраженный через сторону многоугольника.
Радиус описанной окружности ( R )
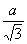
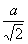
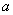
Радиус вписанной окружности ( r )
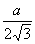
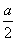
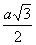
7. Декартовы координаты на плоскости.
Формула 7.1. Координаты середины отрезка. Пусть А( 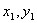
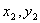
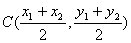
Формула 7.2. Расстояние между точками. Пусть заданы две точки А( 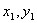
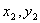
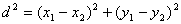
Формула 7.3. Уравнение окружности. Пусть дана окружность с центром в точке 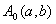
Формула 7.4. Уравнение прямой. Любая прямая в декартовых координатах x , y имеет уравнение вида ax + by + c =0, где a , b , c – некоторые числа. Или иногда встречается уравнение такого вида: y = kx + b . Где k – угловой коэффициент прямой, он так же равен тангенсу острого угла, который образует прямая с осью x .
Теорема 7.1.Параллельность и перпендикулярность прямых. Если у нас есть уравнения двух прямых вида 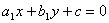
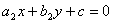
- две прямые параллельны в том и только в том случае, если
;
- совпадают в том и только том случае, если
;
- перпендикулярны в том и только том случае, если
Примечание: в этом случае допускается 0 в знаменателе.
Формула 7.5. Расстояние от точки до прямой. Пусть дана точка A ( 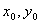
Формула 7.6. Если даны уравнения двух прямых вида 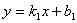
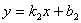
Формула 7.7. Уравнение полуокружности.
— верхняя полуокружность;
— нижняя полуокружность;
— правая полуокружность;
— левая полуокружность.
Определение 8.1. Вектор – направленный отрезок.
📺 Видео
ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать

ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать

Уравнение окружности. Практика. Урок 7. Геометрия 9 классСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать

Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать

УРАВНЕНИЕ ОКРУЖНОСТИ 8 и 9 класс геометрияСкачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать









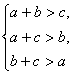
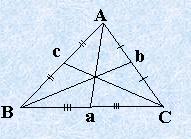
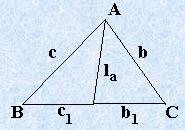
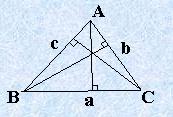
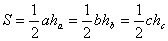
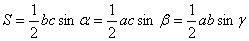
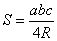
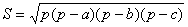
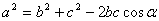
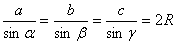
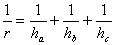
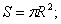
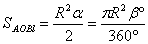
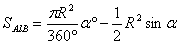
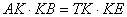

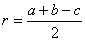
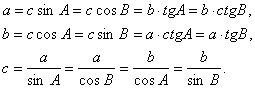
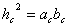
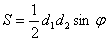
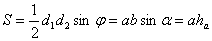
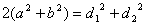
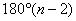
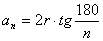
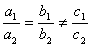 ;
;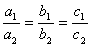 ;
;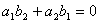
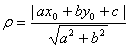
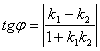
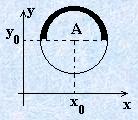
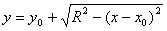 — верхняя полуокружность;
— верхняя полуокружность;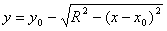 — нижняя полуокружность;
— нижняя полуокружность;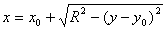 — правая полуокружность;
— правая полуокружность;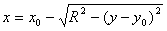 — левая полуокружность.
— левая полуокружность.