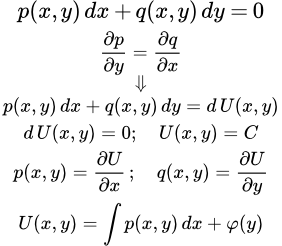Уравнение полных дифференциалов как проверить является ли

Видео:11. Уравнения в полных дифференциалахСкачать

Дифференциальные уравнения в полных дифференциалах

Видео:Дифференциальные уравнения, 6 урок, Уравнения в полных дифференциалахСкачать

Введение

Если найдена такая функция U ( x, y ) , то уравнение принимает вид:
dU ( x, y ) = 0 .
Его общий интеграл:
U ( x, y ) = C ,
где C – постоянная.

Если дифференциальное уравнение первого порядка записано через производную:
,
то его легко привести к форме (1). Для этого умножим уравнение на dx . Тогда . В результате получаем уравнение, выраженное через дифференциалы:
(1) .

Видео:Видеоурок "Уравнение в полных дифференциалах"Скачать

Свойство дифференциального уравнения в полных дифференциалах

Для того, чтобы уравнение (1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось соотношение:
(2) .

Доказательство

Далее мы полагаем, что все функции, используемые в доказательстве, определены и имеют соответствующие производные в некоторой области значений переменных x и y . Точка x ₀ , y ₀ также принадлежит этой области.

Докажем необходимость условия (2).
Пусть левая часть уравнения (1) является дифференциалом некоторой функции U ( x, y ) :
.
Тогда
;
.
Поскольку вторая производная не зависит от порядка дифференцирования, то
;
.
Отсюда следует, что . Необходимость условия (2) доказана.

Докажем достаточность условия (2).
Пусть выполняется условие (2):
(2) .
Покажем, что можно найти такую функцию U ( x, y ) , что ее дифференциал:
.
Это означает, что существует такая функция U ( x, y ) , которая удовлетворяет уравнениям:
(3) ;
(4) .
Найдем такую функцию. Проинтегрируем уравнение (3) по x от x ₀ до x , считая что y – это постоянная:
;
;
(5) .
Дифференцируем по y считая, что x – это постоянная и применим (2):

.
Уравнение (4) будет выполнено, если
.
Интегрируем по y от y ₀ до y :
;
;
.
Подставляем в (5):
(6) .
Итак, мы нашли функцию, дифференциал которой
.
Достаточность доказана.

В формуле (6), U ( x ₀ , y ₀) является постоянной – значением функции U ( x, y ) в точке x ₀ , y ₀ . Ей можно присвоить любое значение.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Как распознать дифференциальное уравнение в полных дифференциалах

Рассмотрим дифференциальное уравнение:
(1) .
Чтобы определить, является ли это уравнение в полных дифференциалах, нужно проверить выполнение условия (2):
(2) .
Если оно выполняется, то это уравнение в полных дифференциалах. Если нет – то это не уравнение в полных дифференциалах.

Пример

Проверить, является ли уравнение в полных дифференциалах:
.

Здесь
, .
Дифференцируем по y , считая x постоянной:

.
Дифференцируем по x , считая y постоянной:

.
Поскольку:
,
то заданное уравнение – в полных дифференциалах.

Видео:Уравнение в полных дифференциалахСкачать

Методы решения дифференциальных уравнений в полных дифференциалах

Метод последовательного выделения дифференциала

Наиболее простым методом решения уравнения в полных дифференциалах является метод последовательного выделения дифференциала. Для этого мы применяем формулы дифференцирования, записанные в дифференциальной форме:
du ± dv = d ( u ± v ) ;
v du + u dv = d ( uv ) ;
;
.
В этих формулах u и v – произвольные выражения, составленные из любых комбинаций переменных.

Пример 1

Ранее мы нашли, что это уравнение – в полных дифференциалах. Преобразуем его:
(П1) .
Решаем уравнение, последовательно выделяя дифференциал.
;
;
;
;

.
Подставляем в (П1):
;
.

Метод последовательного интегрирования

В этом методе мы ищем функцию U ( x, y ) , удовлетворяющую уравнениям:
(3) ;
(4) .

Проинтегрируем уравнение (3) по x , считая y постоянной:
.
Здесь φ ( y ) – произвольная функция от y , которую нужно определить. Она является постоянной интегрирования. Подставляем в уравнение (4):
.
Отсюда:
.
Интегрируя, находим φ ( y ) и, тем самым, U ( x, y ) .

Пример 2

Решить уравнение в полных дифференциалах:
.

Ранее мы нашли, что это уравнение – в полных дифференциалах. Введем обозначения:
, .
Ищем Функцию U ( x, y ) , дифференциал которой является левой частью уравнения:
.
Тогда:
(3) ;
(4) .
Проинтегрируем уравнение (3) по x , считая y постоянной:
(П2)
.
Дифференцируем по y :

.
Подставим в (4):
;
.
Интегрируем:
.
Подставим в (П2):

.
Общий интеграл уравнения:
U ( x, y ) = const .
Объединяем две постоянные в одну.

Метод интегрирования вдоль кривой

Функцию U , определяемую соотношением:
dU = p ( x, y ) dx + q ( x, y ) dy ,
можно найти, если проинтегрировать это уравнение вдоль кривой, соединяющей точки ( x ₀ , y ₀) и ( x, y ) :
(7) .
Поскольку
(8) ,
то интеграл зависит только от координат начальной ( x ₀ , y ₀) и конечной ( x, y ) точек и не зависит от формы кривой. Из (7) и (8) находим:
(9) .
Здесь x ₀ и y ₀ – постоянные. Поэтому U ( x ₀ , y ₀) – также постоянная.

Пример такого определения U был получен при доказательстве свойства уравнения в полных дифференциалах:
(6) .
Здесь интегрирование производится сначала по отрезку, параллельному оси y , от точки ( x ₀ , y ₀ ) до точки ( x ₀ , y ) . Затем интегрирование производится по отрезку, параллельному оси x , от точки ( x ₀ , y ) до точки ( x, y ) .

В более общем случае, нужно представить уравнение кривой, соединяющей точки ( x ₀ , y ₀ ) и ( x, y ) в параметрическом виде:
x ₁ = s ( t ₁) ; y ₁ = r ( t ₁) ;
x ₀ = s ( t ₀) ; y ₀ = r ( t ₀) ;
x = s ( t ) ; y = r ( t ) ;
и интегрировать по t ₁ от t ₀ до t .

Наиболее просто выполняется интегрирование по отрезку, соединяющим точки ( x ₀ , y ₀ ) и ( x, y ) . В этом случае:
x ₁ = x ₀ + ( x – x ₀) t ₁ ; y ₁ = y ₀ + ( y – y ₀) t ₁ ;
t ₀ = 0 ; t = 1 ;
dx ₁ = ( x – x ₀) dt ₁ ; dy ₁ = ( y – y ₀) dt ₁ .
После подстановки, получается интеграл по t от 0 до 1 .
Данный способ, однако, приводит к довольно громоздким вычислениям.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 10-08-2012 Изменено: 02-07-2015

Видео:#Дифуры I. Урок 6. Уравнения в полных дифференциалах (УПД)Скачать

Уравнения в полных дифференциалах

В этой теме мы рассмотрим метод восстановления функции по ее полному дифференциалу, дадим примеры задач с полным разбором решения.

Бывает так, что дифференциальные уравнения (ДУ) вида P ( x , y ) d x + Q ( x , y ) d y = 0 могут содержать в левых частях полные дифференциалы некоторых функций. Тогда мы можем найти общий интеграл ДУ, если предварительно восстановим функцию по ее полному дифференциалу.

Рассмотрим уравнение P ( x , y ) d x + Q ( x , y ) d y = 0 . В записи левой его части содержится дифференциал некоторой функции U ( x , y ) = 0 . Для этого должно выполняться условие ∂ P ∂ y ≡ ∂ Q ∂ x .

Полный дифференциал функции U ( x , y ) = 0 имеет вид d U = ∂ U ∂ x d x + ∂ U ∂ y d y . С учетом условия ∂ P ∂ y ≡ ∂ Q ∂ x получаем:

P ( x , y ) d x + Q ( x , y ) d y = ∂ U ∂ x d x + ∂ U ∂ y d y

∂ U ∂ x = P ( x , y ) ∂ U ∂ y = Q ( x , y )

Преобразовав первое уравнение из полученной системы уравнений, мы можем получить:

U ( x , y ) = ∫ P ( x , y ) d x + φ ( y )

Функцию φ ( y ) мы можем найти из второго уравнения полученной ранее системы:
∂ U ( x , y ) ∂ y = ∂ ∫ P ( x , y ) d x ∂ y + φ y ‘ ( y ) = Q ( x , y ) ⇒ φ ( y ) = ∫ Q ( x , y ) — ∂ ∫ P ( x , y ) d x ∂ y d y

Так мы нашли искомую функцию U ( x , y ) = 0 .

Найдите для ДУ ( x 2 — y 2 ) d x — 2 x y d y = 0 общее решение.

P ( x , y ) = x 2 — y 2 , Q ( x , y ) = — 2 x y

Проверим, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x :

∂ P ∂ y = ∂ ( x 2 — y 2 ) ∂ y = — 2 y ∂ Q ∂ x = ∂ ( — 2 x y ) ∂ x = — 2 y

Наше условие выполняется.

На основе вычислений мы можем сделать вывод, что левая часть исходного ДУ является полным дифференциалом некоторой функции U ( x , y ) = 0 . Нам нужно найти эту функцию.

Так как ( x 2 — y 2 ) d x — 2 x y d y является полным дифференциалом функции U ( x , y ) = 0 , то

∂ U ∂ x = x 2 — y 2 ∂ U ∂ y = — 2 x y

Интегрируем по x первое уравнение системы:

U ( x , y ) = ∫ ( x 2 — y 2 ) d x + φ ( y ) = x 3 3 — x y 2 + φ ( y )

Теперь дифференцируем по y полученный результат:

∂ U ∂ y = ∂ x 3 3 — x y 2 + φ ( y ) ∂ y = — 2 x y + φ y ‘ ( y )

Преобразовав второе уравнение системы, получаем: ∂ U ∂ y = — 2 x y . Это значит, что
— 2 x y + φ y ‘ ( y ) = — 2 x y φ y ‘ ( y ) = 0 ⇒ φ ( y ) = ∫ 0 d x = C

где С – произвольная постоянная.

Получаем: U ( x , y ) = x 3 3 — x y 2 + φ ( y ) = x 3 3 — x y 2 + C . Общим интегралом исходного уравнения является x 3 3 — x y 2 + C = 0 .

Разберем еще один метод нахождения функции по известному полному дифференциалу. Он предполагает применение криволинейного интеграла от фиксированной точки ( x 0 , y 0 ) до точки с переменными координатами ( x , y ) :

U ( x , y ) = ∫ ( x 0 , y 0 ) ( x , y ) P ( x , y ) d x + Q ( x , y ) d y + C

В таких случаях значение интеграла никак не зависит от пути интегрирования. Мы можем взять в качестве пути интегрировании ломаную, звенья которой располагаются параллельно осям координат.

Найдите общее решение дифференциального уравнения ( y — y 2 ) d x + ( x — 2 x y ) d y = 0 .

Проведем проверку, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x :

∂ P ∂ y = ∂ ( y — y 2 ) ∂ y = 1 — 2 y ∂ Q ∂ x = ∂ ( x — 2 x y ) ∂ x = 1 — 2 y

Получается, что левая часть дифференциального уравнения представлена полным дифференциалом некоторой функции U ( x , y ) = 0 . Для того, чтобы найти эту функцию, необходимо вычислить криволинейный интеграл от точки ( 1 ; 1 ) до ( x , y ) . Возьмем в качестве пути интегрирования ломаную, участки которой пройдут по прямой y = 1 от точки ( 1 , 1 ) до ( x , 1 ) , а затем от точки ( x , 1 ) до ( x , y ) :

∫ ( 1 , 1 ) ( x , y ) y — y 2 d x + ( x — 2 x y ) d y = = ∫ ( 1 , 1 ) ( x , 1 ) ( y — y 2 ) d x + ( x — 2 x y ) d y + + ∫ ( x , 1 ) ( x , y ) ( y — y 2 ) d x + ( x — 2 x y ) d y = = ∫ 1 x ( 1 — 1 2 ) d x + ∫ 1 y ( x — 2 x y ) d y = ( x y — x y 2 ) y 1 = = x y — x y 2 — ( x · 1 — x · 1 2 ) = x y — x y 2

Мы получили общее решение дифференциального уравнения вида x y — x y 2 + C = 0 .

Определите общее решение дифференциального уравнения y · cos x d x + sin 2 x d y = 0 .

Проверим, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x .

Так как ∂ ( y · cos x ) ∂ y = cos x , ∂ ( sin 2 x ) ∂ x = 2 sin x · cos x , то условие выполняться не будет. Это значит, что левая часть дифференциального уравнения не является полным дифференциалом функции. Это дифференциальное уравнение с разделяющимися переменными и для его решения подходят другие способы решения.

Видео:12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать

Уравнение в полных дифференциалах

Вы будете перенаправлены на Автор24

Видео:Уравнение в полных дифференциалахСкачать

Уравнение в полных дифференциалах и его решение

Дифференциальное уравнение, имеющее стандартный вид $Pleft(x,yright)cdot dx+Qleft(x,yright)cdot dy=0$, в котором левая часть представляет собой полный дифференциал некоторой функции $Fleft(x,yright)$, называется уравнением в полных дифференциалах.

Уравнение в полных дифференциалах всегда можно переписать в виде $dFleft(x,yright)=0$, где $Fleft(x,yright)$ — такая функция, что $dFleft(x,yright)=Pleft(x,yright)cdot dx+Qleft(x,yright)cdot dy$.

Проинтегрируем обе части уравнения $dFleft(x,yright)=0$: $int dFleft(x,yright)=Fleft(x,yright) $; интеграл от нулевой правой части равен произвольной постоянной $C$. Таким образом, общее решение данного уравнения в неявной форме имеет вид $Fleft(x,yright)=C$.

Для того, чтобы данное дифференциальное уравнение представляло собой уравнение в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие $frac =frac $. Если указанное условие выполнено, то существует такая функция $Fleft(x,yright)$, для которой можно записать: $dF=frac cdot dx+frac cdot dy=Pleft(x,yright)cdot dx+Qleft(x,yright)cdot dy$, откуда получаем два соотношения: $frac =Pleft(x,yright)$ и $frac =Qleft(x,yright)$.

Интегрируем первое соотношение $frac =Pleft(x,yright)$ по $x$ и получаем $Fleft(x,yright)=int Pleft(x,yright)cdot dx +Uleft(yright)$, где $Uleft(yright)$ — произвольная функция от $y$.

Подберем её так, чтобы удовлетворялось второе соотношение $frac =Qleft(x,yright)$. Для этого продифференцируем полученное соотношение для $Fleft(x,yright)$ по $y$ и приравняем результат к $Qleft(x,yright)$. Получаем: $frac left(int Pleft(x,yright)cdot dx right)+U’left(yright)=Qleft(x,yright)$.

Дальнейшее решение таково:

• из последнего равенства находим $U’left(yright)$;
• интегрируем $U’left(yright)$ и находим $Uleft(yright)$;
• подставляем $Uleft(yright)$ в равенство $Fleft(x,yright)=int Pleft(x,yright)cdot dx +Uleft(yright)$ и окончательно получаем функцию $Fleft(x,yright)$.

Чтобы получить частное решение уравнения в полных дифференциалах, начальное условие $y=y_ $ при $x=x_ $ нужно подставить в общее решение $Fleft(x,yright)=C$. Получаем $Fleft(x_ ,y_ right)=C$. Таким образом, частное решение имеет вид $Fleft(x,yright)=Fleft(x_ ,y_ right)$.

Видео:✓Дифференцируемая функция. Дифференциал | матан #032 | Борис ТрушинСкачать

Интегрирующие множители

Если для дифференциального уравнения $Pleft(x,yright)cdot dx+Qleft(x,yright)cdot dy=0$ условие $frac =frac $ не выполняется, то такое уравнение не является уравнением в полных дифференциалах. Но в некоторых случаях его можно преобразовать в уравнение в полных дифференциалах посредством умножения на некоторую функцию $mu left(x,yright)$, которая называется интегрирующим множителем.

Будем искать интегрирующий множитель в следующих двух простейших случаях:

• когда он зависит только от $x$, то есть $mu =mu left(xright)$;
• когда он зависит только от $y$, то есть $mu =mu left(yright)$.

Первый случай имеем тогда, когда отношение $frac<frac -frac > =phi _ left(xright)$ зависит только от $x$. Тогда интегрирующий множитель можно найти по следующей формуле $mu =e^ <int phi _left(xright)cdot dx > $.

Второй случай имеем тогда, когда отношение $frac<frac -frac >

=phi _ left(yright)$ зависит только от $y$. Тогда интегрирующий множитель можно найти по следующей формуле $mu =e^ <-int phi _left(yright)cdot dy > $.

В обоих формулах для интегрирующего множителя допустимо взять какое-то конкретное значение неопределенного интеграла. Если интегрирующий множитель найти удалось, то на него следует умножить данное дифференциальное уравнение, представленное в стандартном виде. После этого оно становится дифференциальным уравнением в полных дифференциалах, и к нему можно применить соответствующий метод решения.

Видео:ОДУ 1 порядка. Уравнения в полных дифференциалахСкачать

Алгоритмы решения

Рассмотренный метод решения может быть представлен в виде следующего алгоритма:

1. Данное дифференциальное уравнение следует представить в стандартном виде $Pleft(x,yright)cdot dx+Qleft(x,yright)cdot dy=0$. Оно может быть уравнением в полных дифференциалах. Чтобы убедиться в этом, следует проверить условие $frac=frac$. Если это условие не выполняется, нужно перейти к поиску интегрирующего множителя. Иначе выполнение алгоритма продолжаем.
2. Вычисляем интеграл $Vleft(x,yright)=int Pleft(x,yright)cdot dx $ и выбираем для него какое-то простое значение.
3. Находим частную производную $V’_ left(x,yright)=fracVleft(x,yright)$.
4. Находим разность $U’left(yright)=Qleft(x,yright)-V’_ left(x,yright)$.
5. Интегрируем $U’left(yright)$ по $y$, находим $Uleft(yright)$ и выбираем для неё какое-то простое значение.
6. Записываем искомую функцию $Fleft(x,yright)=Vleft(x,yright)+Uleft(yright)$.
7. Записываем общее решение $Fleft(x,yright)=C$ и частное решение $Fleft(x,yright)=Fleft(x_ ,y_ right)$, где $y=y_ $ при $x=x_ $ — начальное условие.

Поиск интегрирующего множителя может быть представлен в виде следующего алгоритма:

1. Вычисляем вспомогательную функцию $R=frac-frac$.
2. Находим функции $phi _ left(xright)=frac$ и $phi _ left(yright)=frac

   $. Если функция $phi _ left(xright)$действительно зависит только от $x$, то интегрирующий множитель находим по формуле $mu =e^ <int phi _left(xright)cdot dx > $. Если функция $phi _ left(yright)$ действительно зависит только от $y$, то интегрирующий множитель находим по формуле $mu =e^ <-int phi _left(yright)cdot dy > $. В обоих случаях для интегрирующего множителя выбираем какое-то конкретное значение неопределенного интеграла.

3. Если интегрирующий множитель найти удалось, то умножаем на него данное дифференциальное уравнение, представленное в стандартном виде. После этого оно становится дифференциальным уравнением в полных дифференциалах и можно переходить на соответствующий алгоритм его решения. Если интегрирующий множитель найти не удалось, то дифференциальное уравнение должно решаться иным методом.

Дано дифференциальное уравнение, имеющее следующий вид:

[left(5cdot y^ +13cdot y^ +6cdot yright)cdot dx+left(10cdot xcdot y^ +23cdot xcdot y-2cdot y+6cdot x-4right)cdot dy=0.]

Найти его общее решение. Найти также его частное решение для начального условия $y=3$ при $x=2$.

Данное дифференциальное уравнение имеет вид $Pleft(x,yright)cdot dx+Qleft(x,yright)cdot dy=0$, где $Pleft(x,yright)=5cdot y^ +13cdot y^ +6cdot y$, $Qleft(x,yright)=10cdot xcdot y^ +23cdot xcdot y-2cdot y+6cdot x-4$. Оно может быть уравнением в полных дифференциалах. Поэтому проверяем условие $frac =frac $.

Находим частные производные: $frac =15cdot y^ +26cdot y+6$, $frac =10cdot y^ +23cdot y+6$. Условие $frac =frac $ не выполняется. Следовательно, данное дифференциальное уравнение не является уравнением в полных дифференциалах. Поэтому переходим к поиску интегрирующего множителя.

Находим вспомогательную функцию $R=frac -frac $. Получаем$R=15cdot y^ +26cdot y+6-10cdot y^ -23cdot y-6=5cdot y^ +3cdot y$.

Находим функции: $phi _ left(xright)=frac =frac <5cdot y^+3cdot y> <10cdot xcdot y^+23cdot xcdot y-2cdot y+6cdot x-4> $ и $phi _ left(yright)=frac

=frac <5cdot y^+3cdot y> <5cdot y^+13cdot y^ +6cdot y> $.

Выполняем упрощение найденных функций посредством сокращения дробей. Оказывается, что для функции $phi _ left(xright)$ сокращение невозможно. Функция $phi _ left(yright)$ в результате сокращения получает вид $phi _ left(yright)=frac $. При этом она зависит только от $y$ и поэтому подходит для определения интегрирующего множителя.

Интегрирующий множитель находим по формуле $mu =e^ <-int phi _left(yright)cdot dy > $. Получаем: $mu =e^ <-int phi _left(yright)cdot dy > =e^<-int frac cdot dy > =e^ =frac <e^> =frac $. Выбираем конкретное значение $mu =frac $.

Умножаем полученный интегрирующий множитель на данное дифференциальное уравнение:

[frac <5cdot y^+13cdot y^ +6cdot y> cdot dx+frac <10cdot xcdot y^+23cdot xcdot y-2cdot y+6cdot x-4> cdot dy=0.]

После деления многочленов имеем:

[left(5cdot y^ +3cdot yright)cdot dx+left(10cdot xcdot y+3cdot x-2right)cdot dy=0. ]

Получили новое дифференциальное уравнение, в котором $Pleft(x,yright)=5cdot y^ +3cdot y$, $Qleft(x,yright)=10cdot xcdot y+3cdot x-2$.

Снова проверяем условие $frac =frac $: получаем $frac =10cdot y+3$, $frac =10cdot y+3$. Условие $frac =frac $ выполняется. Следовательно, новое дифференциальное уравнение является уравнением в полных дифференциалах. Переходим к алгоритму его решения.

Вычисляем интеграл: $Vleft(x,yright)=int Pleft(x,yright)cdot dx =int left(5cdot y^ +3cdot yright)cdot dx =$

[=left(5cdot y^ +3cdot yright)cdot int dx =left(5cdot y^ +3cdot yright)cdot x=5cdot xcdot y^ +3cdot xcdot y.]

[V’_ left(x,yright)=frac Vleft(x,yright)=frac left(5cdot xcdot y^ +3cdot xcdot yright)=10cdot xcdot y+3cdot x.]

[U’left(yright)=Qleft(x,yright)-V’_ left(x,yright)=10cdot xcdot y+3cdot x-2-10cdot xcdot y-3cdot x=-2.]

Интегрируем $U’left(yright)$ по $y$ и находим $Uleft(yright)=int left(-2right)cdot dy =-2cdot y$.

Находим результат: $Fleft(x,yright)=Vleft(x,yright)+Uleft(yright)=5cdot xcdot y^ +3cdot xcdot y-2cdot y$.

Записываем общее решение в виде $Fleft(x,yright)=C$, а именно:

[5cdot xcdot y^ +3cdot xcdot y-2cdot y=C.]

Находим частное решение $Fleft(x,yright)=Fleft(x_ ,y_ right)$, где $y_ =3$, $x_ =2$:

[Fleft(2,3right)=5cdot 2cdot 3^ +3cdot 2cdot 3-2cdot 3=90+18-6=102.]

Частное решение имеет вид: $5cdot xcdot y^ +3cdot xcdot y-2cdot y=102$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 30 11 2021

📺 Видео

Дифференциальные уравнения в полных дифференциалах (часть 1)Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Дифференциальные уравнения в полных дифференциалах.Скачать

Дифференциальные уравнения в полных дифференциалах| poporyadku.schoolСкачать

Уравнение в полных дифференциалах, примеры, решениеСкачать

Полный дифференциалСкачать

Приведение дифференциальных уравнений к полным дифференциаламСкачать

Видеоурок "Интегрирующий множитель"Скачать